基于分层法的石墨烯增强功能梯度Timoshenko梁动力特性有限元分析

黄立新,周小云,滕靓媚

(1.广西大学土木建筑工程学院,广西 南宁,530004;2.广西大学工程防灾与结构安全教育部重点实验室,广西 南宁,530004)

新型纳米材料石墨烯具有优异的力学性能,其理论拉伸强度和杨氏模量分别高达130 GPa、1 TPa[1],是Q235钢相应值的300倍和5倍,故而常用作纳米复合材料的增强体。段笑[2]针对碳纤维表面的惰性、光滑、非极性且与树脂黏合度差等问题,向其中引入了石墨烯。研究结果表明,石墨烯的加入可以增强复合材料的导电性、抗压性。并且,当石墨烯含量为0.2%时,其对复合材料剪切性能、弯曲强度、冲击韧性的增强作用最佳。郭准等[3]的研究结果表明,将聚甲基丙烯酸甲酯与石墨烯复合所得材料的性能较聚甲基丙烯酸甲酯有明显改善。当加入的石墨烯质量含量为1.5%时,聚甲基丙烯酸甲酯/石墨烯复合材料断口呈现出典型的韧性断裂特征。Parashar 等[4]利用代表性体积元方法研究了石墨烯纳米复合材料的屈曲现象,将石墨烯在原子尺度上建模并把聚合物作为一个连续体。与纯聚合物相比,石墨烯增强聚合物的屈曲强度显著提高。在石墨烯质量含量仅为6%的情况下,石墨烯/聚合物纳米复合材料的屈曲强度较纯聚合物相应值提高了26%。

功能梯度材料作为一种新型的非均质复合材料,其成分和性能在空间上连续变化,从而能更好地适应不同的环境及使用要求[5]。Yang等[6]通过添加少量石墨烯片(graphene platelets,GPLs ) 得到功能梯度纳米复合梁。相关研究结果表明,GPLs对纳米复合材料梁的屈曲和后屈曲具有显著增强作用。Zhao等[7]研究了GPLs 增强功能梯度多孔拱在静力和径向均布压力共同作用下的动力不稳定性。数值计算结果表明,加入少量GPLs可以有效提升功能梯度多孔拱的稳定性。Feng等[8]研究了石墨烯纳米片沿厚度方向非均匀分布的功能梯度聚合物复合梁的非线性自由振动。结果表明,在聚合物基体中加入少量的GPLs作为增强剂,可以显著提高梁的固有频率。Sahmani等[9]研究了轴向加载多层功能梯度石墨烯片增强复合材料(graphene platelet-reinforced composite,GPLRC)纳米梁在预屈曲和后屈曲区域的非线性振动。结果表明,在预屈曲、屈曲或后屈曲状态下,GPLRC纳米束的非线性频率均随GPLs质量分数的增加而增大。此外,黄干云等[10]通过将材料划分为若干层,针对功能梯度材料的断裂力学问题开展研究。本课题组[11]借助分层模型,对功能梯度材料的进行了有限元分析。在已有研究的基础上,本文拟采用分层法并结合有限元分析来考察GPLs增强功能梯度Timoshenko梁的动力特性。通过数值算例验证有限元软件ABAQUS建模的准确性,分析分层数与单元尺寸比例的合理性,着重探讨GPLs的分布形式、质量含量、几何形状和尺寸以及边界条件对Timoshenko梁自由振动的影响。

1 石墨烯增强功能梯度材料模型及其性能参数

基于分层法针对石墨烯增强功能梯度Euler梁进行有限元静力分析,导出有效材料性能的计算公式,详细推导过程参见文献[12]。作为研究石墨烯增强功能梯度Timoshenko梁动力问题的基础,本文简要列出了一些概念和公式。

1.1 石墨烯增强功能梯度Timoshenko梁的结构模型

图1所示为石墨烯增强功能梯度Timoshenko梁的结构模型。该梁的长度为l、宽为b、高为h。GPLs分布在环氧树脂材料中,其质量含量WGPL随着梁的高度发生连续变化。GPLs沿梁厚度方向z呈现线性、第一类抛物线、第二类抛物线及均布等4种分布形式[6,13-14]。其中,线性分布形式下的WGPL分布函数为:

(1)

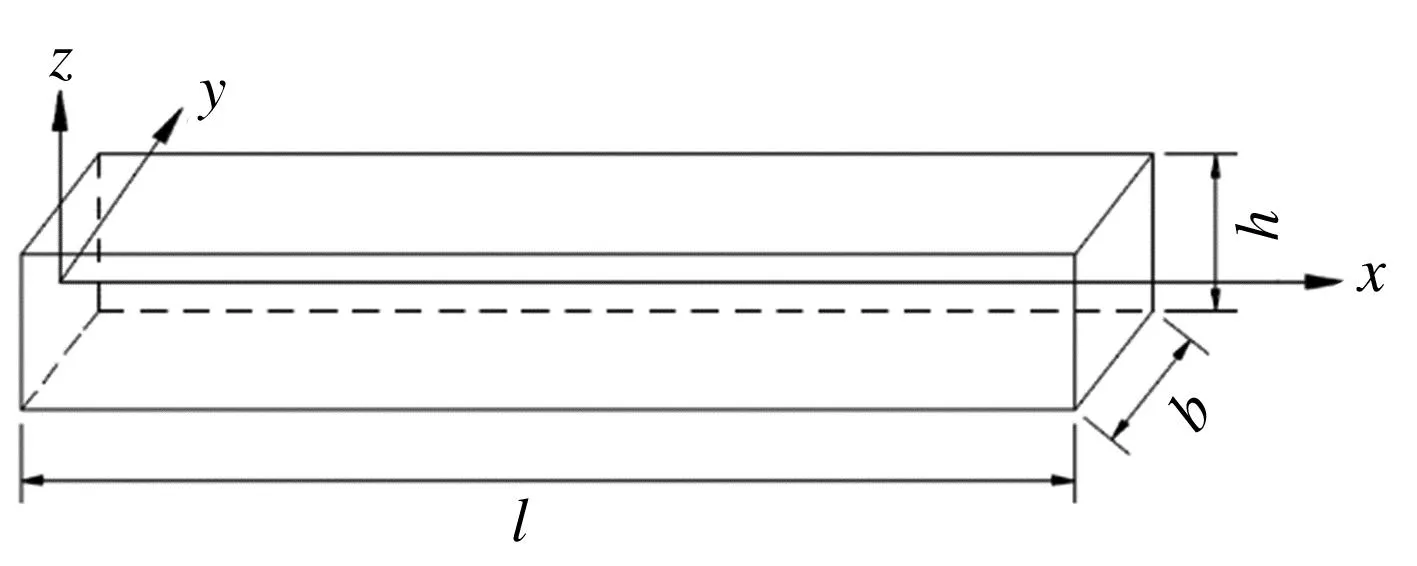
图1 石墨烯增强功能梯度Timoshenko梁

第一类抛物线形式下的WGPL分布函数为:

(2)

此时,GPLs的质量含量在顶面和底面处最大,在中间平面处最小。第二类抛物线形式下的WGPL分布函数为:

(3)

此时,GPLs的质量含量在顶面和底面处最小,在中间平面处最大。均布形式下的WGPL分布函数为:

(4)

表1 梯度指标λi与之间的关系

1.2 石墨烯增强功能梯度Timoshenko梁的有效材料参数

在进行结构分析之前,需要确定石墨烯功能梯度Timoshenko梁所需的材料参数。有效弹性模量计算基于修正后的Halpin-Tsai微观力学模型[13],即

(5)

其中

(6)

(7)

(8)

(9)

式(6)～式(9)中,EM、EGPL分别表示功能梯度梁基体及石墨烯的杨氏模量;lGPL、bGPL、tGPL分别表示GPLs的平均长度、平均宽度和平均厚度。根据混合率法则[6,15],石墨烯增强复合材料的泊松比vC和质量密度ρC可分别表示为

vC=vGPLVGPL+vM(1-VGPL)

(10)

ρC=ρGPLVGPL+ρM(1-VGPL)

(11)

式(10)～式(11)中,VGPL为GPLs的体积含量,有

(12)

其中,ρGPL是GPLs的质量密度,ρM是功能梯度梁基体的质量密度。

对于GPLs呈线性分布(LDPC)的Timoshenko梁,将式(1)代入式(12)可以得到相应的石墨烯体积含量为

(13)

将式(6)～式(9)及式(13)代入式(5)可得到石墨烯增强复合材料的杨氏模量,即

(14)

将式(13)分别代入式(10)和式(11)可以得到石墨烯增强复合材料的泊松比和质量密度,即

(15)

(16)

同理可得,GPLs呈第一类抛物线分布(PDPRSC)的Timoshenko梁的杨氏模量、泊松比和密度表达式分别为

(17)

(18)

(19)

GPLs呈第二类抛物线分布(PDPRMC)的Timoshenko梁的杨氏模量、泊松比和密度表达式分别为

(20)

(21)

(22)

GPLs呈均匀分布(UDPC)的Timoshenko梁的杨氏模量、泊松比和密度表达式分别为

(23)

(24)

(25)

2 基于分层法的有限元模型

在不同GPLs分布形式下,石墨烯增强复合材料的杨氏模量、泊松比和质量密度沿厚度方向呈现多种变化。故而对相关模型进行有限元分析时,需将石墨烯增强复合材料沿厚度方向划分为若干层,不同层的杨氏模量、泊松比和质量密度均不相同,但同层的杨氏模量和泊松比为常数。运用有限单元对各层进行网格划分,即可建立有限元模型。将石墨烯增强功能梯度Timoshenko梁沿厚度方向分为n层,不同GPLs分布形式下每层复合材料的杨氏模量、泊松比及质量密度取值见表2,并且采用4节点四边形板单元(S4R)离散。

表2 各层的材料参数

忽略阻尼影响,系统的自由振动方程表示为

(26)

(27)

(28)

式(27)～式(28)中,单元质量矩阵Me和单元刚度矩阵Ke分别为

(29)

(30)

其中,D表示弹性矩阵,有

(31)

式中,杨氏模量E(z)和泊松比v(z)是关于厚度方向坐标z的函数。针对不同的GPLs分布形式,由表2获得每层薄板的杨氏模量、泊松比和质量密度,再代入式(31)即可进行有限元计算。

式(26)自由振动方程的解可以假设为以下形式

(32)

(33)

3 计算与讨论

对于本文中的所有算例,除非另有说明,否则均采用以下数值和条件:

基于分层法的有限元计算中,根据表2的公式计算每一层的杨氏模量、泊松比和质量密度;模型长度、宽度和高度分别为10个单位、2个单位和2个单位,跨高比l/h=5,GPL质量分数为0.25%,支座条件为两边简支;GPLs的lGPL=2.5 μm,bGPL=1.5 μm,tGPL=1.5 nm;GPLs和环氧树脂材料参数vM=0.34,vGPL=0.186,ρM=1200 kg/m3,ρGPL=1060 kg/m3,EM=2.85 GPa,EGPL=1010 GPa;为了便于表述,基频的无量纲化结果表达式[15]如下

(34)

3.1 分层数与单元尺寸比例对有限元计算结果的影响

进行有限元分析时,在满足计算精度要求的同时也要保证计算效率。针对Timoshenko梁的自由振动问题,采用 4节点四边形板单元(S4R)进行有限元建模,同时考虑各种单元尺寸比例。通过与文献[15]给出的自由振动无量纲解析解进行对比,分析分层数和单元尺寸比例的合理性。在有限元计算中,通过表2的公式计算每一层的杨氏模量和泊松比。

表3 分层数对于石墨烯功能梯度Timoshenko梁自由振动频率的影响

图2 功能梯度梁有限元网格

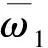
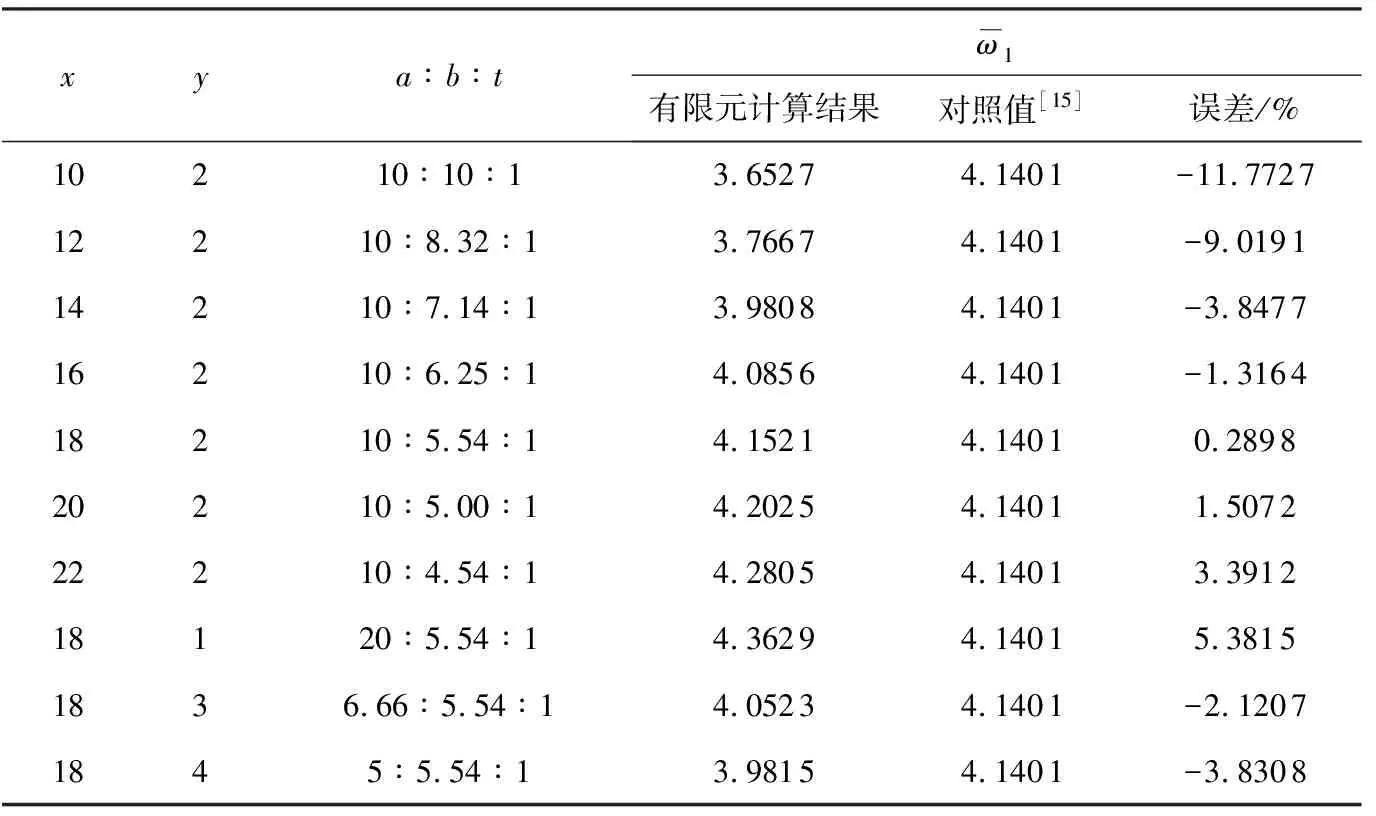
表4 单元尺寸比例对于石墨烯功能梯度Timoshenko梁自振频率的影响

3.2 石墨烯增强功能梯度Timoshenko梁自由振动的有限元分析

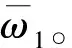
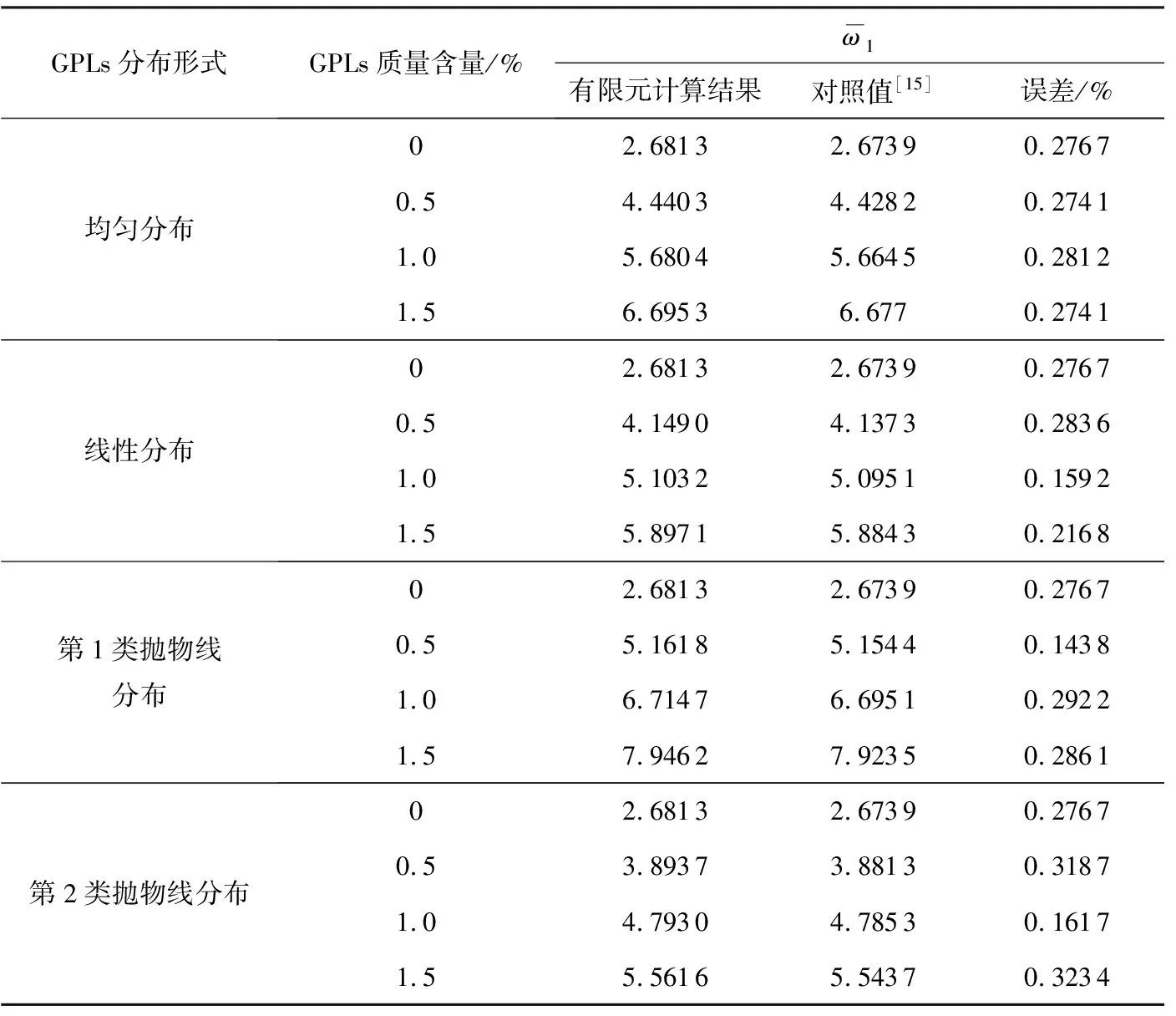
表5 GPLs增强功能梯度Timoshenko梁的自由振动频率

3.3 不同GPLs含量对有限元计算结果的影响

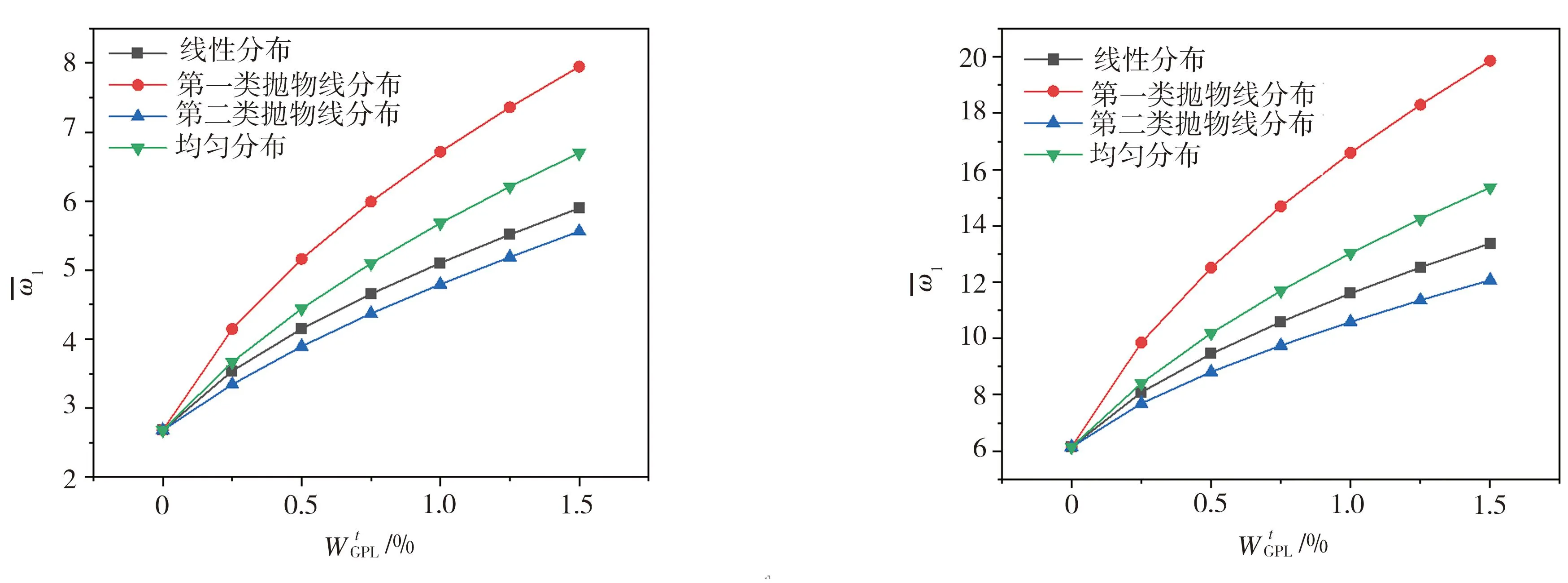
算例选取相关参数如下:梁长l为0.5 m,梁宽b为0.1 m,梁高h为0.1 m;跨高比l/h为5;GPLs的总质量含量范围为0～1.5%,增量为0.25%;梁的支座条件如图3所示,分别为两端简支、两端固定、悬臂和一端固定、一端简支。经计算,得到石墨烯增强功能梯度Timoshenko梁自由振动无量纲基频随GPLs质量含量变化的曲线如图4所示。其中当GPLs的质量含量为0时,Timoshenko梁是纯环氧树脂梁。从图4可以看出,加入少量的石墨烯可以大幅度提高石墨烯增强功能梯度Timoshenko梁的基频,这是因为石墨烯能够较大地提高梁的刚度。当GPLs总质量含量不变时,GPLs第一类抛物线分布的Timoshenko梁具有最大的基频,而GPLs出现第二类抛物线分布时,基频最小。与其他三种分布形式相比,GPLs第一类抛物线分布形式的增强刚度效果最好。换句话说,在梁的上下表面分布更多的GPLs是增加梁刚度的最有效方法。

(a)简支梁 (b) 两端固定梁

(a)简支梁 (b) 两端固定梁

在多种GPLs的质量含量、分布形式以及各种边界条件下,采用有限元方法计算石墨烯增强功能梯度Timoshenko梁自由振动的基频,计算结果列于表6。从表6中可以看出,在其他条件不变的情况下,不同支座条件下的复合梁基频也不同。基频由大到小的顺序对应的支座条件分别为两端固定、一端固定一端简支、两端简支和悬臂,这种变化规律也已经在图4中得到展现。

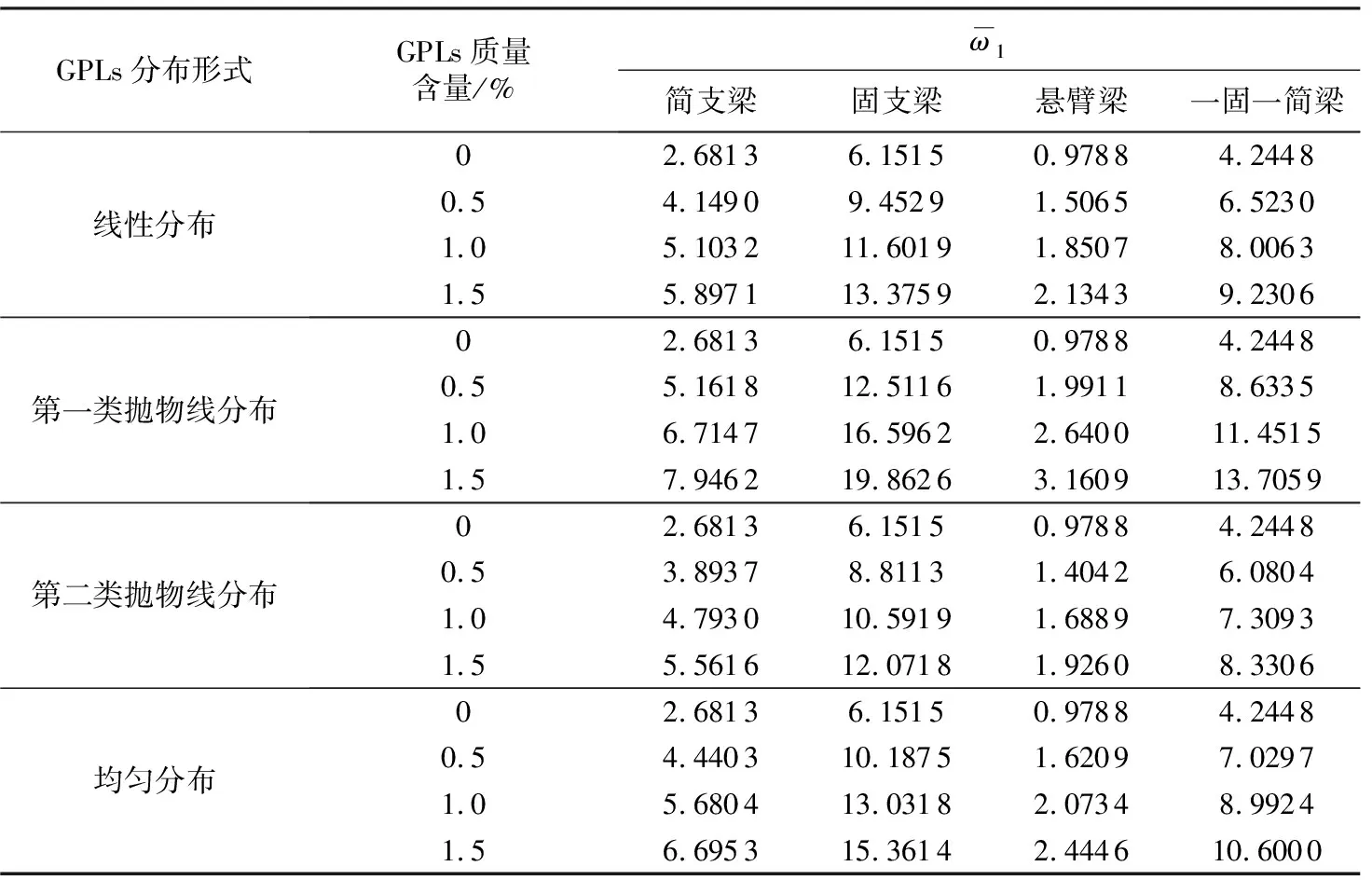
表6 自由振动频率有限元计算结果

3.4 GPLs几何形状和尺寸对有限元计算结果的影响

如图5所示,考虑三种几何形状和尺寸的GPLs,即长度lGPL保持不变,长宽比分别取lGPL/bGPL=1、lGPL/bGPL=3和lGPL/bGPL=5,然后研究长宽比lGPL/bGPL和长厚比lGPL/tGPL的变化对功能梯度Timoshenko梁自由振动基频的影响。

(a)lGPL/bGPL=1 (b)lGPL/bGPL=3

设定石墨烯质量含量为1.5%,Timoshenko梁的支座条件为两端简支,GPLs的分布形式包括线性分布、第一类抛物线分布、第二类抛物线分布和均布分布,石墨烯增强功能梯度Timoshenko梁自由振动基频的变化情况如图6所示。从图6中可以看出,随着长厚比lGPL/tGPL的增加,梁的基频增加,并且随着长厚比lGPL/tGPL的不断增加,梁基频增加的速度趋缓。当长厚比lGPL/tGPL超过1000之后,梁基频增加不明显。在相同条件下,当lGPL/tGPL=1时,梁基频最大,当lGPL/tGPL=5时,梁基频最小。图6中梁基频的变化趋势还表明,GPLs呈第一类抛物线分布的功能梯度Timoshenko梁具有最大的基频。

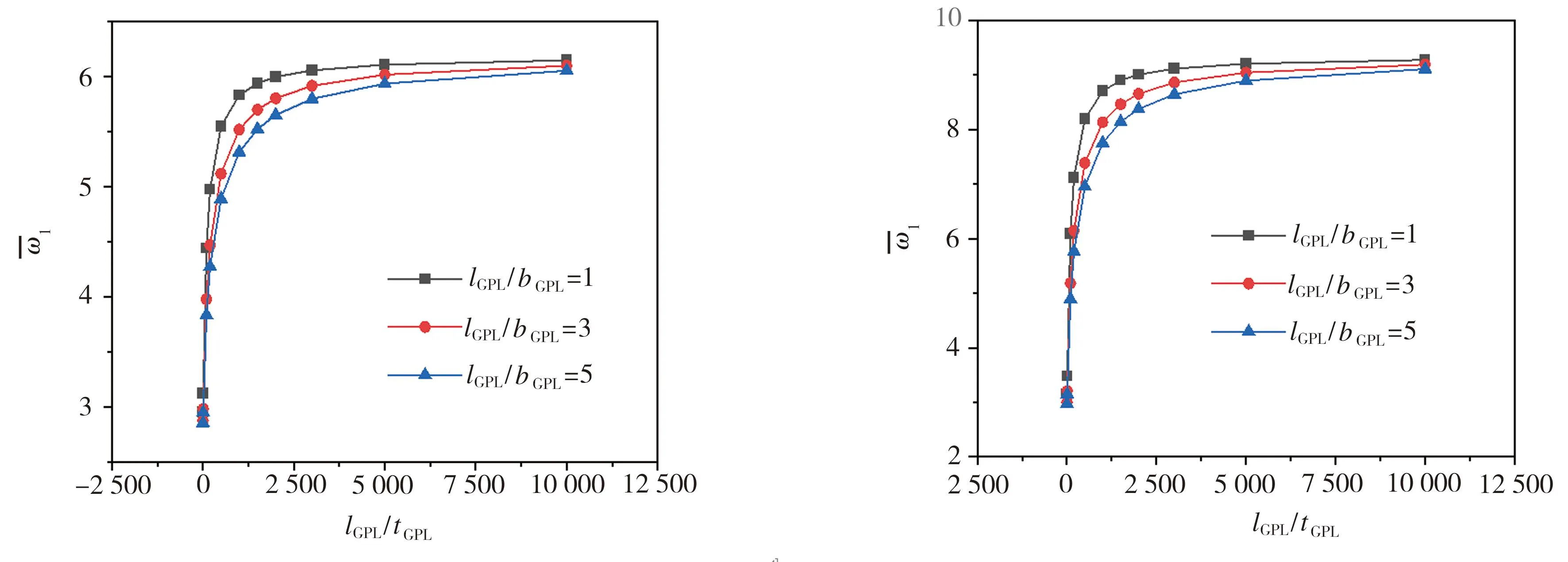
(a)线性分布 (b) 第一类抛物线分布

4 结语

本文基于有限元方法,针对石墨烯增强功能梯度Timoshenko梁进行动力特性分析。首先沿梁的厚度方向进行分层,然后根据修正后Halpin-Tsai微观力学模型和混合率法则分别得到每层的弹性模量、泊松比和质量密度等材料参数,最后每一层采用4节点四边形板单元(S4R)划分网格,通过计算得到Timoshenko梁的频率。借助数值算例,分析了分层数和单元尺寸比例的合理性,研究GPLs分布形式、质量含量、几何形状和尺寸以及梁边界条件对Timoshenko梁自由振动的影响。结果表明,加入少量的石墨烯能显著提高Timoshenko梁自由振动的频率,这表明引入少量石墨烯就能有效地增加梁的刚度;石墨烯的分布形式对Timoshenko梁的动力特性有明显的影响。当石墨烯呈第一类抛物线分布形式,即在梁的上下部位分布更多的石墨烯时,梁的频率增幅最大,这是增加Timoshenko梁刚度的最有效方法;石墨烯的几何形状和尺寸对Timoshenko梁的动力特性有较大影响。具体地说,在给定总石墨烯质量含量的情况下,Timoshenko梁的频率随着长厚比lGPL/tGPL的增加而增大,当长厚比lGPL/tGPL超过1000之后,梁频率变化不明显。至于石墨烯几何形状的影响,与长方形石墨烯相比,正方形石墨烯强化的Timoshenko梁具有更高的频率。