指定任务空间的并联机构尺度参数多目标优化方法

石灿玉,邵 华,张 华

(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3.武汉科技大学精密制造研究院,湖北 武汉,430081)

并联机构具有高刚度、高精度和高速度的优点,广泛应用于电子、食品、医药等工业生产领域[1-3]。不同类型的并联机构差异很大,并联机构的设计可分为类型综合[4]和尺度参数设计[5]。其中,尺度参数设计是并联机构研究领域的热点问题之一。

在对并联机构进行尺度参数设计时,首先要评估并联机构在工作空间内的性能[6]。Salisbury等[7]定义了雅可比矩阵的条件数用于评估并联机构的灵巧性[8]。Gosselin等[9]提出了整个工作空间内的雅可比条件数指标GCI,但存在机构转动和平动时雅可比矩阵量纲不统一的问题[10]。Tsai等[11]定义了机构的传递特性和可操作性。Liu等[12]定义了描述机构位形的局部传递指标LTI以及工作空间内整体的运动/力传递性能的全局传递指标GTI,二者均独立于参考坐标系[13]。不过,以上研究大多基于并联机构在全局可达工作空间的性能分布,并不能准确描述指定任务空间的性能分布。此外,因机构的全局可达工作空间通常比工程应用场合的指定任务空间大得多,故而易导致计算过程中的计算量和计算时间增加。在正确评估工作空间内并联机构性能分布的基础上,可采用优化设计方法获得最优的尺度参数。一类方法是通过构造参数设计空间,利用搜索法找到机构性能评价最佳的尺度参数。如Bi等[14]提出了一种无量纲模型的性能图谱方法,基于运算搜索方法获得性能最优的尺度参数。Xie等[15]应用性能图谱方法优化了并联机构尺度参数并实现了大转角输出。另一类方法是通过智能算法来优化尺度参数。如Wu等[16]利用遗传算法对biglide和Ragnar并联机构的刚度性能、运动学性能、工作空间和动力学性能进行了优化。Che等[17]采用进化算法来优化 4-RUPaR并联机构尺度参数,达到最大化工作空间的目的。文世坤[18]使用人工蜂群算法优化4-PRPaU并联机构的尺度参数。但是,在工程应用过程中,将并联机构的尺度参数无量纲化后,很难考虑尺度参数如基座、移动平台或链接的最大/最小尺度等的约束。有鉴于此,本文提出一种新的基于指定任务空间的尺度参数多目标优化方法,即考虑并联机构的指定工作空间和实际几何约束,采用一种新指标来评估并联机构在指定任务空间上的性能分布并构建新的参数设计空间,从而获得机构尺度参数的最优解。通过对Delta并联机构实施基于指定任务空间的尺度参数优化,将本文所提方法与传统的全局可达空间尺度参数优化方法进行比较,以期为并联机构尺度参数设计的研究提供参考。

1 指定任务空间的尺度参数多目标优化方法

使用归一化方法[19]来获得有限的设计空间时,尺度参数会因无量纲化而导致物理意义丢失,同时也难以保持尺度参数与指定工作空间的联系。要解决这些问题,需要建立一种新的方法,既能将并联机构的尺度参数缩小到有限的范围,又能保持尺度参数与指定任务空间的联系。因为指定任务空间的并联机构旋转自由度即弧度本身就是一种无量纲参数,所以主要针对并联机构在指定任务空间的平移度长度单位即标准尺度长度来保持联系。使用归一化方法将标准尺度长度与尺度参数无量纲化,可获得基于指定任务空间有限范围的参数设计空间,而并联机构的尺度参数与指定任务空间也保持着一定的比例关系。将指定任务空间转变为同比例缩放的尺度参数,就能保持尺度参数与指定任务空间的联系。

在本研究中,首先基于并联机构尺度参数和指定任务空间构建新的参数设计空间;然后检验其中的尺度参数是否满足约束与逆运动学方程,剔除超出约束和逆运动学方程无实数解的参数;最后基于本文提出的指定任务空间的性能指标来评估并联机构的性能,采用搜索法得到并联机构的最优尺度参数,并验证机构的运动/力传递性能。该方法的技术路线如图1所示,详细过程如下:

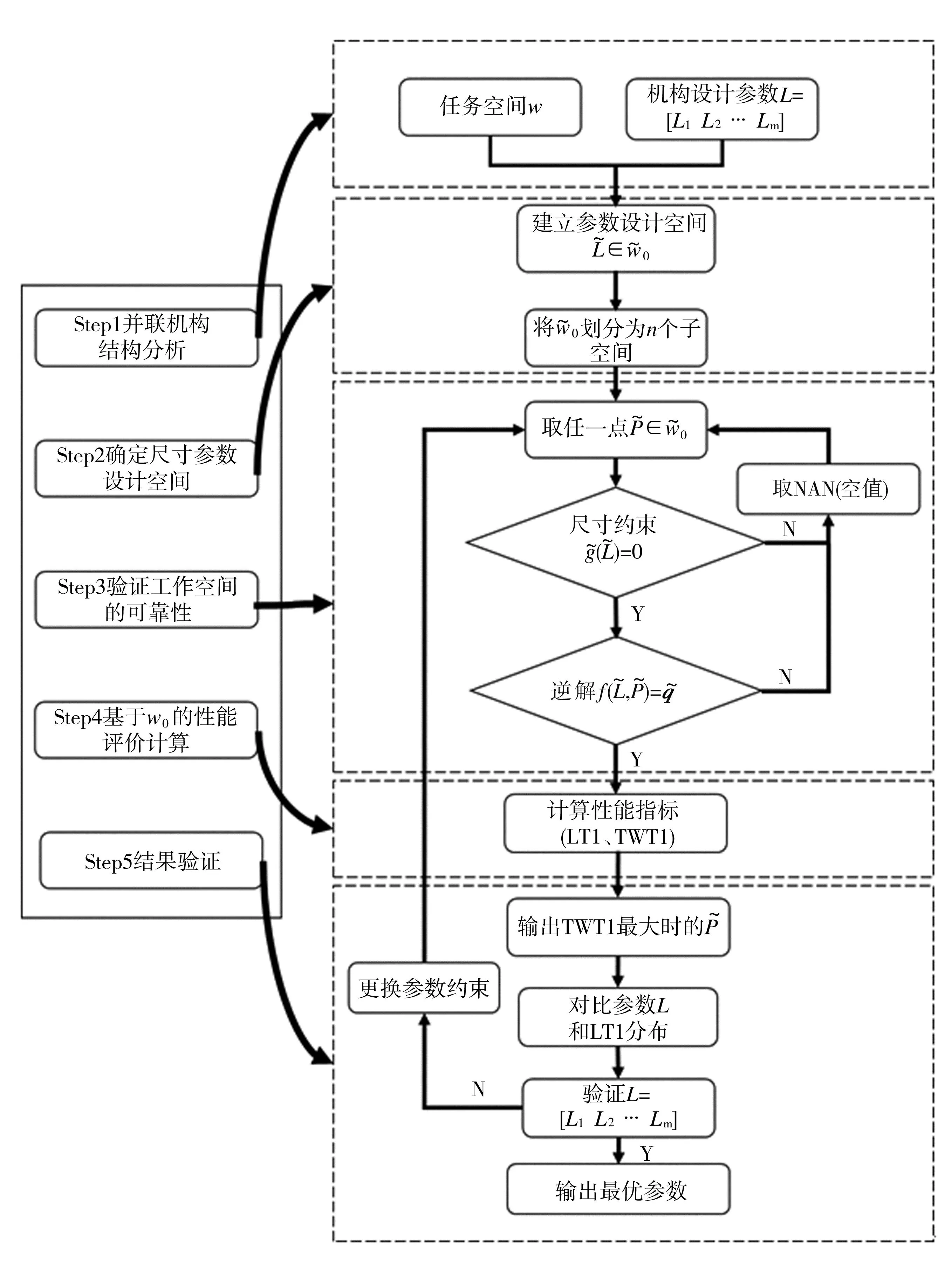
图1 任务空间尺度参数多目标优化方法流程图

步骤1)建立尺度参数的设计空间。理论上尺度参数可以从0到∞,但这样不利于寻求尺度参数最优值。因此,为了同时描述指定任务空间w,将采用归一化方法在指定任务空间和尺度参数上建立新的参数设计空间;

步骤2)通过考虑尺度参数的约束,验证尺度参数是否满足约束;

步骤3)计算机构的逆运动学方程,删除逆运动学方程没有实数解的参数,主要是因为该参数无法到达指定任务空间w;

步骤4)采用本文提出的一个指定任务空间的性能指标来评估并联机构的性能分布,然后找出性能指标最优的尺度参数;

步骤5)计算最优尺度参数在指定任务空间上的性能分布,验证优化效果。

1.1 尺度参数的设计空间

使用归一化方法建立并联机构的有限参数设计空间。假设要优化的并联机构有m个尺度参数,可以用线性化形式表示,有

L=[L1L2…Lm]L∈m

(1)

式中,Li是并联机构的第i个设计参数,例如移动平台的半径、连杆长度等,数字m是指待优化的尺度参数总数。

提出一个包含指定任务空间和尺度参数L的新设计空间来解决归一化后尺度参数与指定任务空间联系丢失的问题。例如,可以引入额外的标准尺度长度Lm+1=1 m,并且可以基于标准尺度长度Lm+1来表示指定任务空间w。对于任一P∈w,它由移动平台的平移向量p和旋转向量v组成,即

P=[pv],P∈w

(2)

位姿点P可以表示为

(3)

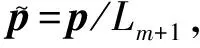
D=(L1+L2+…+m+Lm+1)/(m+1)

(4)

di=Li/D(i=1,2,…,m+1)

(5)

(6)

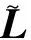
(7)

由式(5)和式(6)可以得出

d1+d2+…+dm+dm+1=m+1

(8)

Li=diLm+1/dm+1(i=1,2,…,m)

(9)

1.2 参数约束判断

并联机构的尺度参数有许多约束,如几何约束、奇异性约束等,这些约束可以用相关参数的几何方程和长度限制不等式来描述,表示为参数L的约束函数,即

g(L)=0

(10)

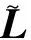
(11)

1.3 判断任务点到达的参数空间

f(L,P)=q

(12)

该式也可以转化为归一化形式

(13)

1.4 任务空间中的性能评估

在评估并联机构的指定任务空间性能之前,必须计算指定任务空间的性能指标。局部传递指标(LTI)和全局传递指标(GTI)主要针对全局可达空间的并联机构,并不适合指定的任务空间,故而采用指定任务空间传递指标(TWTI),有

(14)

式中,Ψ是具有参数L的并联机构任务工作空间中每个位姿点P的LTI指数。Γ表示LTI在指定任务空间中的平均分布,较大的Γ表示该并联机构在指定任务空间上具有更好的运动/力传递能力。任务空间传递指标TWTI也可以标准化形式使用,即

(15)

2 案例-Delta并联机构的优化

Delta是一个应用非常广泛的三平移并联机构,许多研究者基于全局可达空间对其进行了尺度参数优化[20]。本研究基于指定任务空间上的Delta并联机构,实现机构性能与尺度参数约束的综合多目标尺度参数优化,并与传统全局可达空间优化方法进行比较。

2.1 尺度参数的设计空间

图2所示为Delta并联机构。该并联机构采用对称原理设计,由静平台A1A2A3、动平台C1C2C3和三个支链AiBiCi(i=1,2,3)组成,γ1、α1分别为正、负传动角。连杆A1B1、A2B2与A3B3长度相等,连杆BiCi(i=1,2,3)的长度也相等,动平台C1C2C3的半径通常固定以便于在移动平台上安装操作器,为方便研究,本文将其设定为200 mm。设定静平台A1A2A3的半径L1,支链A1B1和B1C1的长度分别为L2和L3。则需优化的参数可以表示为

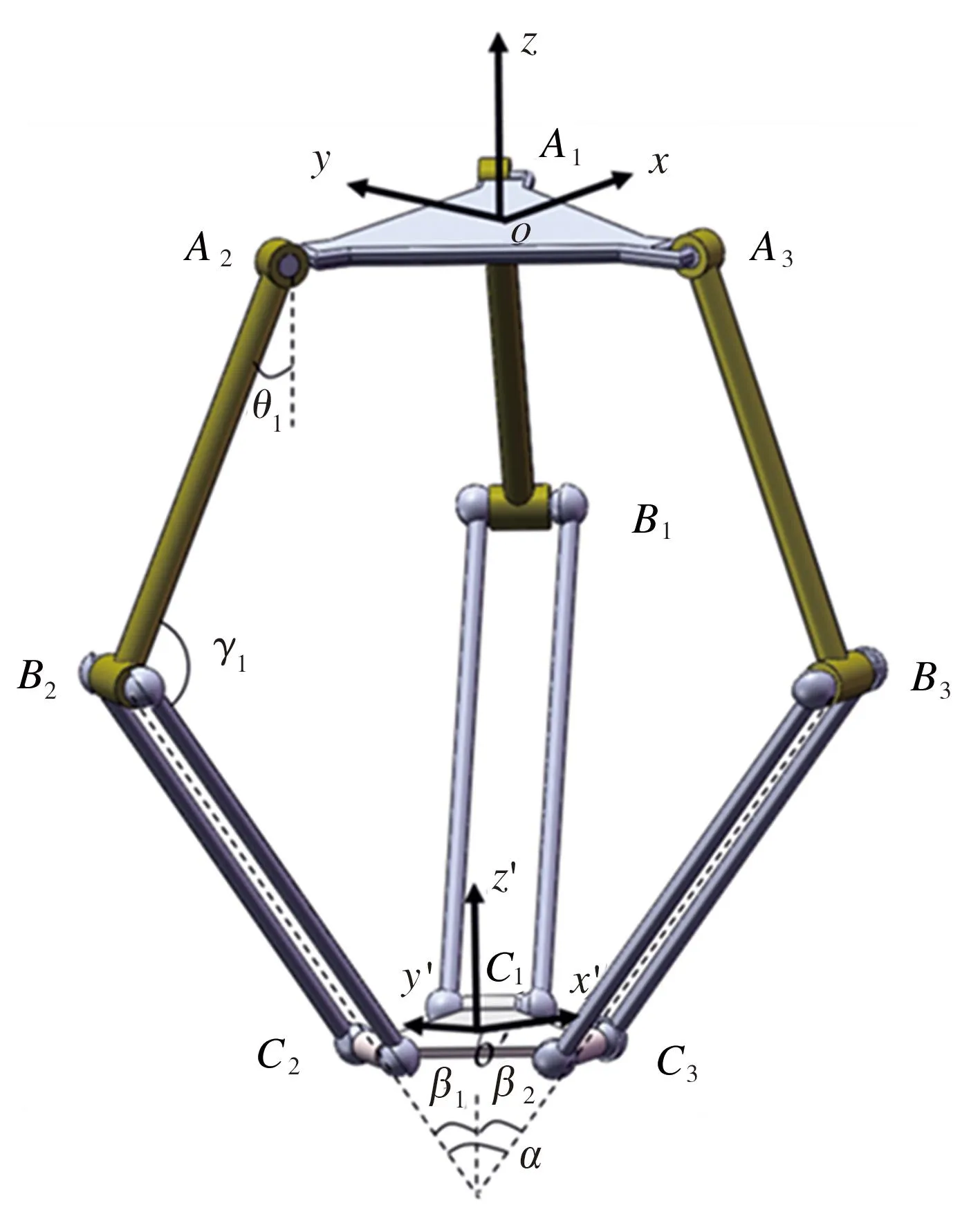
图2 Delta并联机构示意图

L=[L1L2L3]

(16)

Delta并联机构具有3个平移度,工作空间为三维立方体。指定任务空间w尺度为400 mm×400 mm×800 mm,附加参数L4为200 mm,则w可以表示为2L4×2L4×4L4。对于任何点P∈w,有

P=[pv]

(17)

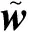
D=(L1+L2+L3+L4)/4

(18)

di=Li/D(i=1,2,3,4)

(19)

(20)

(21)

(22)

2.2 参数约束判断

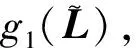
(23)

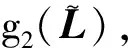
(24)

2.3 逆解

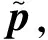
2.4 性能指标

λi=|sinγi|

(25)

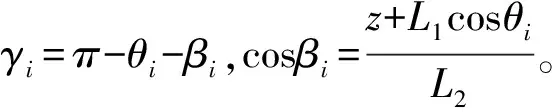
ηi=|sinαi|

(26)

Ψ=min{λiηi},(i=1,2,3)

(27)

任务空间性能指标TWTI可以描述为

(28)

2.5 参数优化结果

2.5.1 参数优化结果分析

机构不同约束条件下的不同优化结果如下:

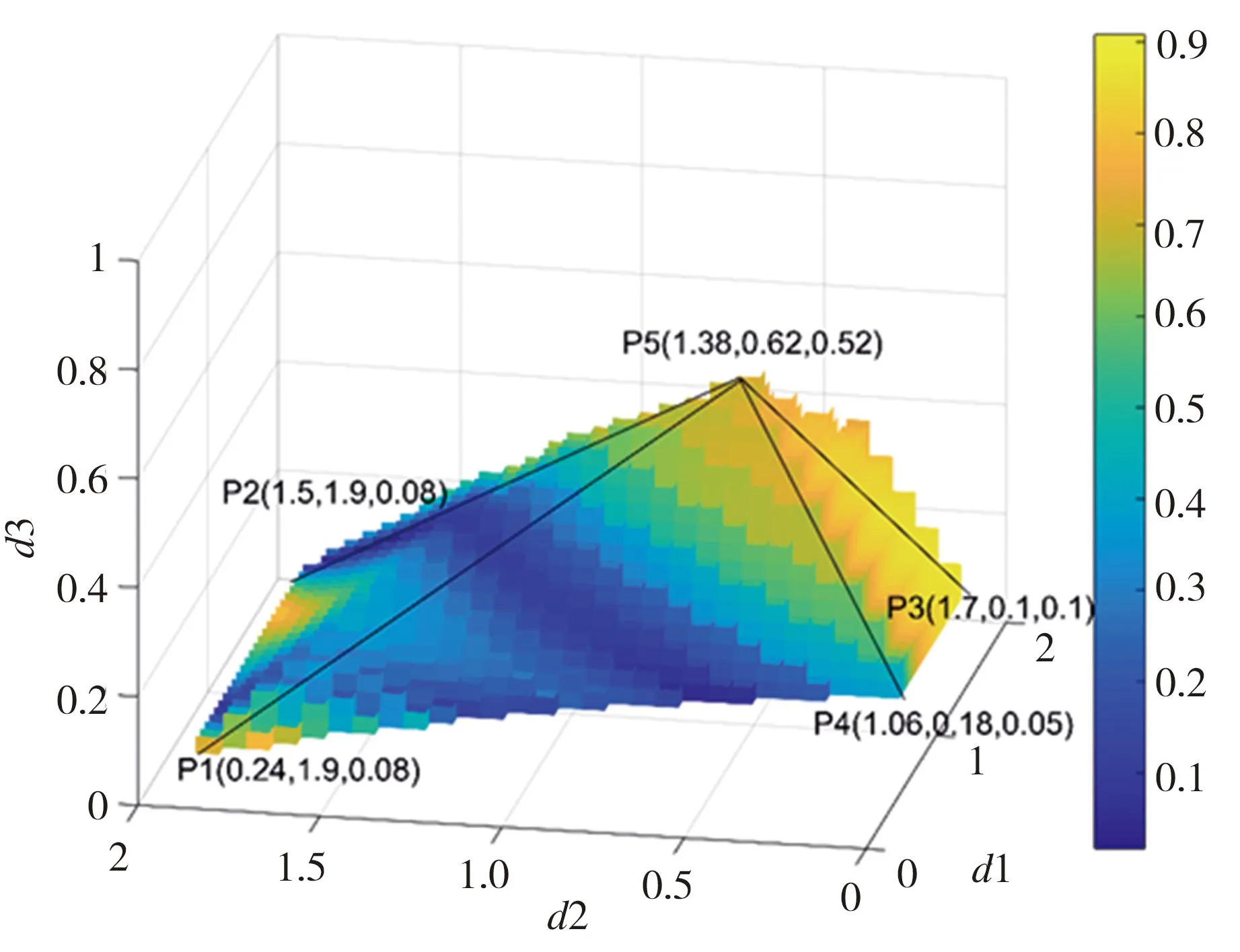
图3 任务工作空间传输指数随约束的分布

图4 具有参数限制的TWTIΓ的分布

2.5.2 优化结果比较

为了确定本文所提优化方法在并联机构的指定任务空间上能否获得更好的效果,在此对其及传统方法所得最优尺度参数结果的LTI分布进行比较。选取传统的全局可达空间优化方法的尺度参数为:L1=200 mm,L2=600 mm、L3=800 mm。图5所示为不同方法和约束条件下的最优参数LTI分布。其中图5(a)给出了传统全局可达空间方法下的最优参数的LTI分布,最大LTI为0.8503,LTI平均值为0.672;图5(b)给出了第一个约束条件下的最优参数的LTI分布,最大LTI为0.9288,LTI平均值为0.9083;图5(c)给出了第二个约束条件的最优参数LTI分布情况,最大LTI为0.9826,LTI均值为0.7971。所有的最优尺度参数和相应的LTI结果见表1。由表1可见,无论是指定任务空间上的最大LTI还是平均LTI,都明显优于传统的全局可达空间方法,这证明了指定任务空间的尺度参数优化方法的有效性。在不受机构长度限制的情况下,指定任务空间上的平均LTI可以达到0.9083,但静平台和支链A1B1的尺度过大,当指定任务空间w仅为400 mm×400 mm×800 mm时,它们分别超过4500 mm和7200 mm,这对于工程应用是不实际的。在第二种约束情况下,对静平台的半径和支链A1B1和B1C1的长度,给出了最大尺度约束800 mm,并且最优参数L1,L2和L3都满足约束,同时特定任务空间上的平均LTI为0.7971,表明该机构的良好性能。

表1 不同方法和约束条件下的优化结果

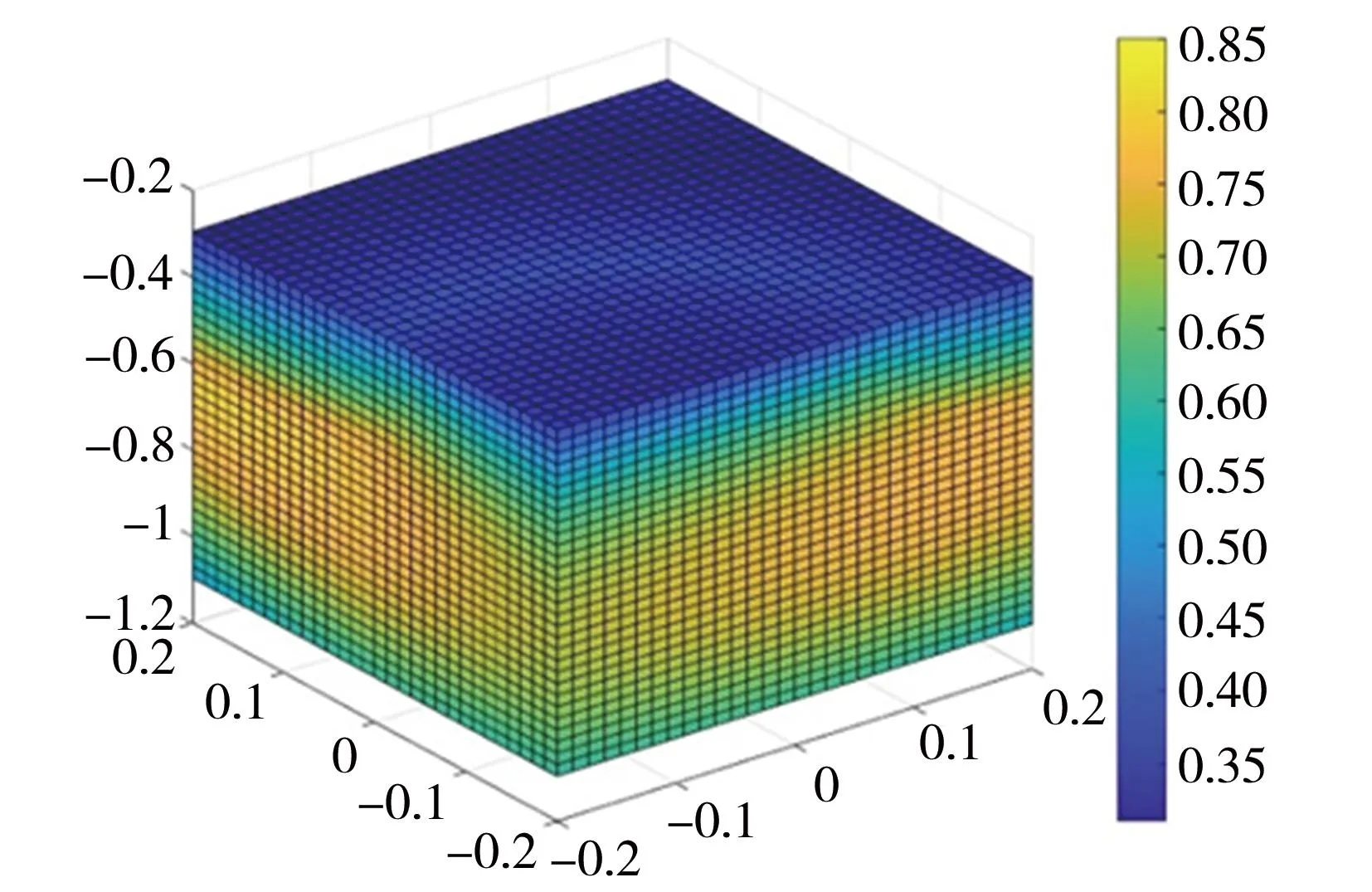
(a)传统全局可达空间方法的LTI分布

图6～图8所示为不同优化方法下y-z、x-z和x-y三个截面上任务空间中心的LTI分布。以图8为例,图8(a)为传统全局可达空间方法的最优尺度参数LTI分布图的x-y截面,参数最大值为0.84,最小值为0.72。图8(b)为第一种约束条件下最优尺度参数LTI分布图的x-y截面,参数最大值为0.925,最小值为0.905。图8(c)为第二种约束条件下最优尺度参数LTI分布图的x-y截面,参数最大值为0.97,最小值为0.92。相比之下,第二种约束情况在并联机构运动/力传递性能方面明显优于传统全局可达空间优化方法和第一种约束情况。通过上述三种方法的比较,表明本文所提出的方法在不同约束的指定任务空间中明显比传统全局可达优化方法更有效。证明了指定任务空间优化方法可以有效地求解具有尺度参数约束的并联机构的最优尺度参数。

(a)传统的全局可达空间方法 (b) 第一约束条件 (c) 第二约束条件

(a)传统的全局可达空间方法 (b) 第一约束条件 (c) 第二约束条件

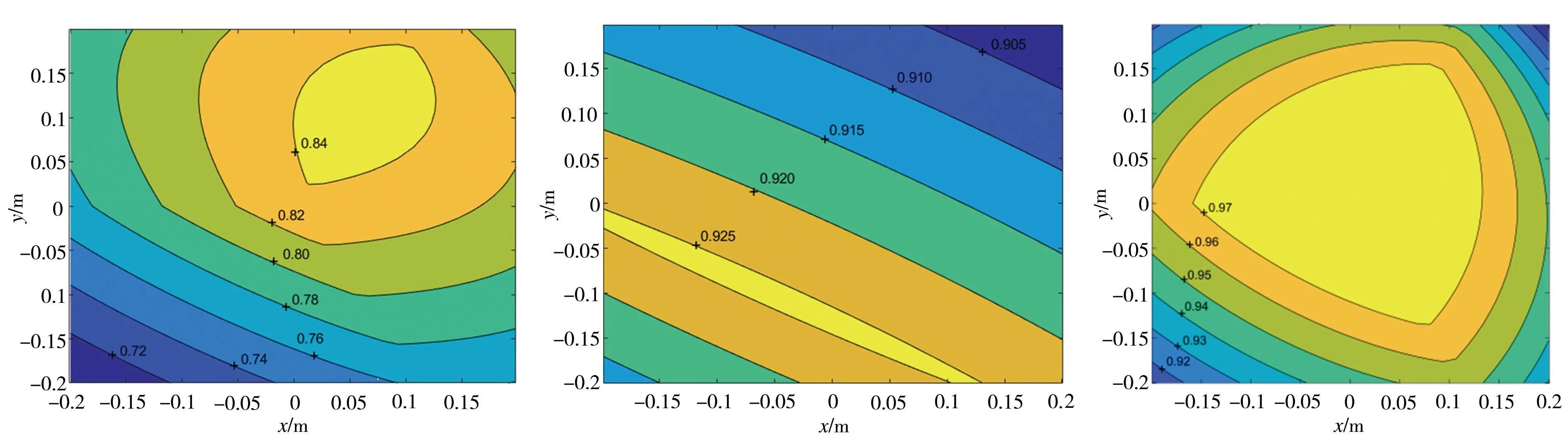
(a)传统全局可达空间方法 (b) 第一约束条件 (c) 第二约束条件

3 结语

本文提出了一种基于指定任务空间的并联机构尺度参数多目标优化方法,并借助机构的几何约束和性能评估获得了最优参数。针对某些工程应用中传统的并联机构全局可达空间尺度参数优化设计方法不适用于指定任务空间的问题,通过改进尺度参数设计空间方法,引入TWTI性能指标来评估指定任务空间下的性能,使得指定任务空间下的并联机构具有更好的性能。该方法可以针对个性化的工程应用需求引入不同的尺度参数约束要求,实现机构性能与尺度参数约束的综合多目标尺度参数优化,满足差异化需求,达到并联机构的最佳性能。以Delta并联机构为例,与传统的全局可达空间优化方法相比,利用本文新方法时,指定空间的LTImax从0.850 3提高到0.982 6,LTIave从0.672提高到0.7971,新优化方法的有效性得到充分证明。该方法适用于并联机构指定任务空间下的尺度参数优化。下一步将考虑利用智能算法提高计算效率,使其更适用于并联机构的尺度参数优化问题。