欠驱动灵巧手的优化设计及仿真分析

张 林,王兴东,孙 伟,龚彩云

(武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081)

随着机械手在工业生产和日常生活中的广泛应用,对其抓取能力提出了更高要求。欠驱动灵巧手通过合理的结构设计以少于手指关节自由度的驱动器控制手的运动[1-2],因此其结构相对简单、系统可靠性更高,而且利用弹簧或耦合机构实现多级抓取,可赋予欠驱动灵巧手自适应抓取能力[3]。目前,欠驱动灵巧手的研究成果有很多,其中,HIT[4]、SDM[5]、Softhand[6]等采用的是腱绳拮抗驱动方式,但这类灵巧手在抓取过程中手指位姿不定,不能独立控制手指各关节转动,只能实现包络抓取[7]。连杆驱动式灵巧手因传动效率高、响应快、关节刚度高、输出稳定且可控而被大量应用[8],例如SARAH[9-10]、已进入市场的Robotiq Hand[11]等。此外,金波等[12]研制出一种新型自适应果蔬采摘欠驱动机械手,实现了果蔬的无损采摘;Luo等[13]基于线性平行机构设计了具有混合抓取模式的两指欠驱动灵巧手VGS;Tang等[14]提出一种模块化欠驱动多指机械手,可根据不同工况配置手指的数量和参数;Sun等[15]基于变胞原理设计了一种结构简单、通用性强的欠驱动机械手。

大部分机械手在精确抓取小物体时有一定的难度[16],因此设计出结构简单、抓取力大且稳定、对不同形状的抓取物具有自适应性的欠驱动灵巧手是十分必要的。为此,本文提出一种新型欠驱动灵巧手机构,对其关键参数进行设计优化。该灵巧手不仅可以实现包络抓取,还可以完成指尖抓取,其单指采用模块化设计,方便单指的更换,同时采用协同耦合方法设计手指与手掌,使得灵巧手对不同尺寸、不同形状的抓取物均具有较强的自适应性。

1 单指机构的结构及工作原理

欠驱动机械手单指的原结构如图1(a)所示。单指的工作原理如下:在弹性元件的约束下,手指未与抓取物接触时只有一个自由度;驱动单指时,近指节率先与抓取物接触,完全接触后形成机械限位;随后,驱动力克服近指节与中指节之间弹性元件的阻尼力,弹性元件释放出一个自由度,中指节继续运动直至完全接触后形成机械限位;最后,驱动力克服中指节与远指节之间弹性元件的阻尼力,弹性元件释放一个自由度,远指节继续运动直至完全接触,从而完成了单指的全包络抓取,见图2(a)。由于其本身的限制,原机构只能实现包络抓取,故本研究添加一套平行四连杆机构优化以上设计,四连杆机构见图1(b),优化后的手指机构见图1(c)。指尖抓取时,由于弹性元件以及平行机构的约束,在未接触到抓取物时,手指只有一个自由度,驱动单指时,指尖与抓取物接触形成机械限位,从而实现指尖抓取,如图2(b)所示。包络抓取适用于大且重的物体,指尖抓取适用于小且轻的物体。

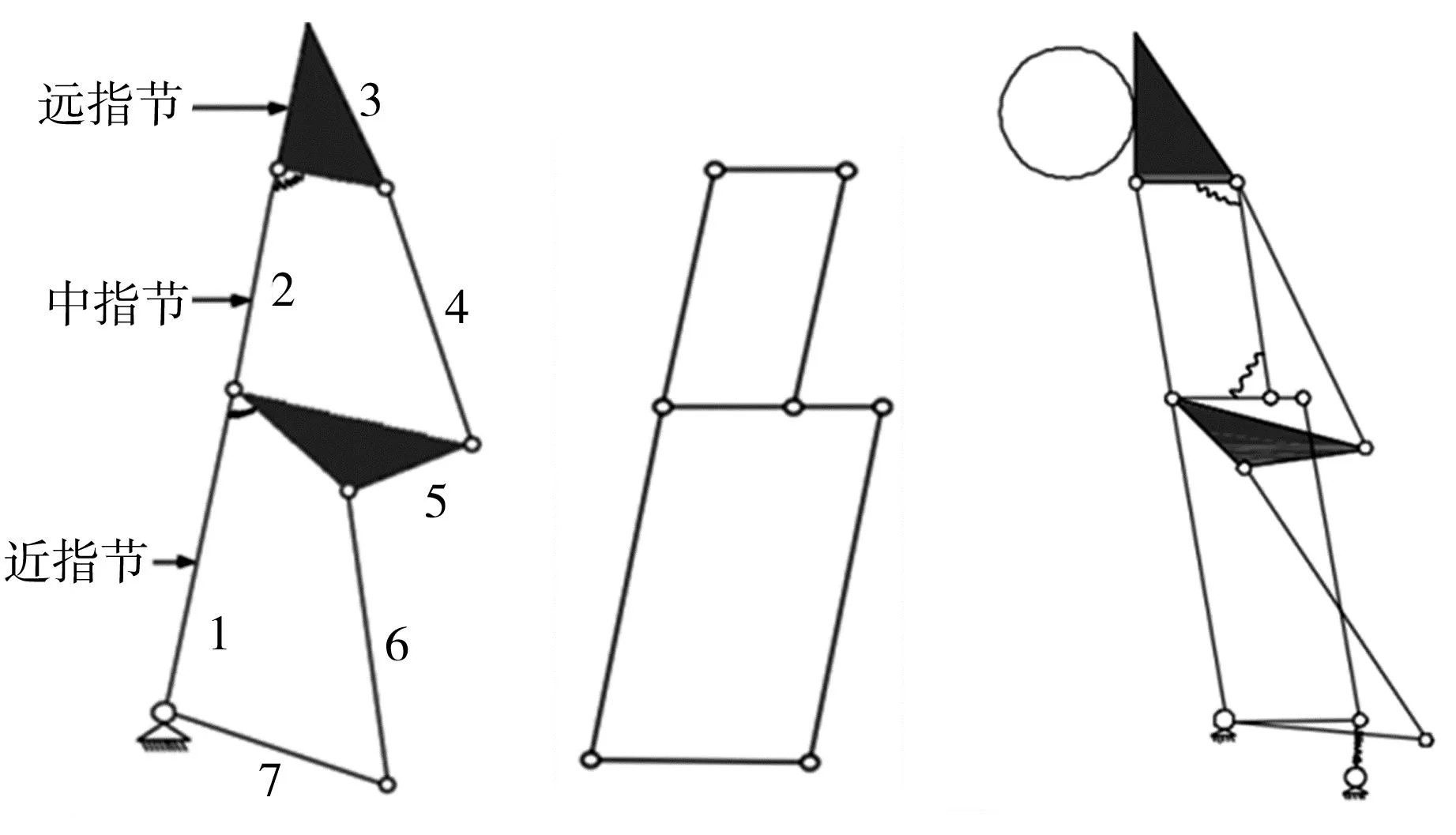
(a)机构简图(优化前) (b)平行四连杆机构 (c)机构简图(优化后)

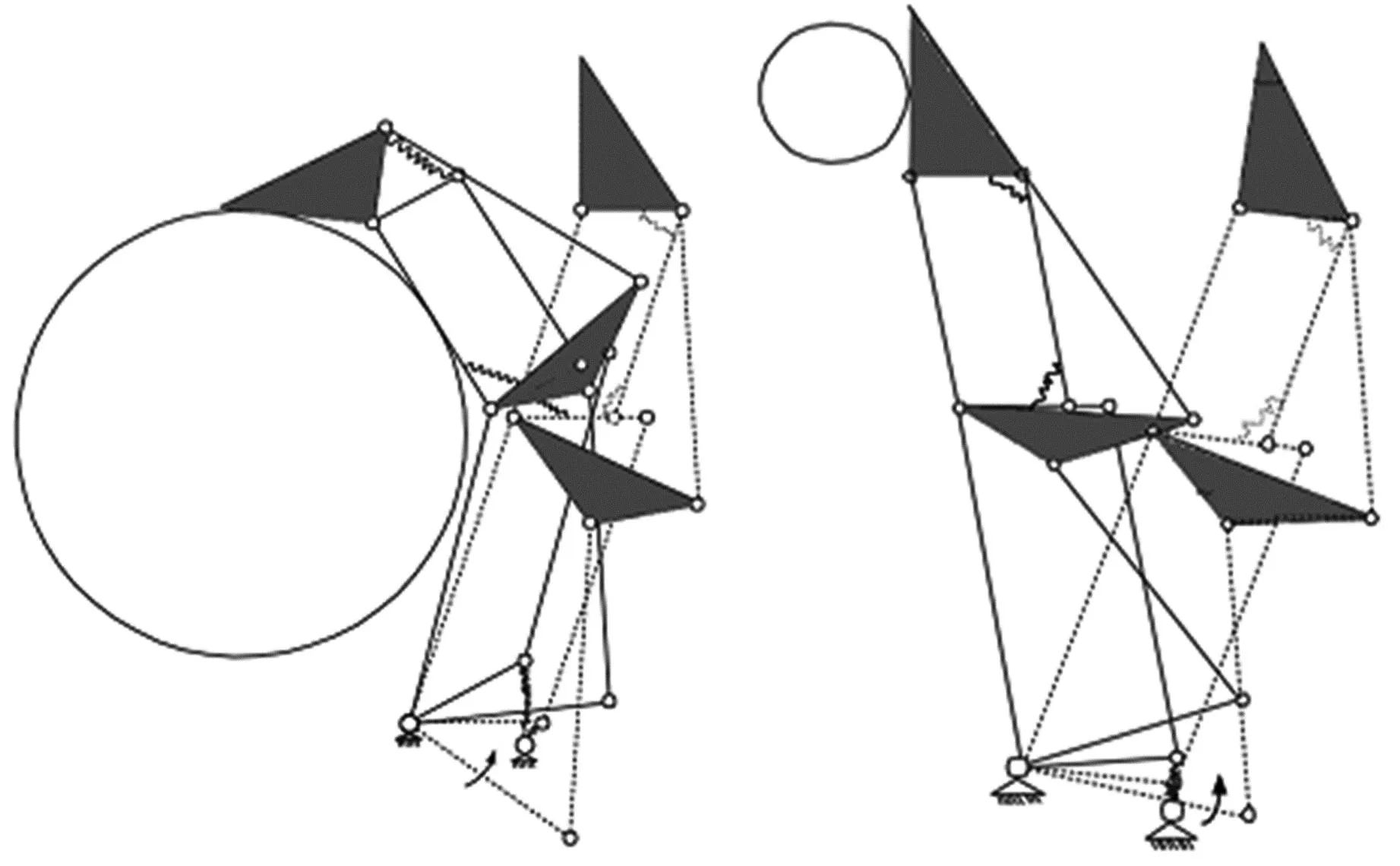
(a)包络抓取 (b)指尖抓取

2 单指机构的接触力模型

2.1 指尖抓取接触力模型

首先建立指尖抓取接触力模型,如图3所示。假设单指机构和抓取物组成的系统为一个刚体系统,在以下的接触力分析中忽略各关节的重量以及各关节运动副间的摩擦。

图3 指尖抓取接触力模型

根据力矩平衡原理[17]可得:

f3=To1p1/[(l1+l2)sinθ1+k3]

(1)

式中:To1p1为施加在连杆o1p1上的驱动力矩,l1、l2分别为近指节、中指节的长度,f3为远指节(即指尖)接触力,k3为指尖接触点到销轴的垂直距离,θ1为近指节的关节转角。

2.2 包络抓取接触力模型

首先针对手指各关节建立接触力分析数学模型。通过数学模型可以得到输入扭矩和各关节施加到物体上的抓取力之间的对应关系。手指包络抓取时的接触力模型及参数见图4。

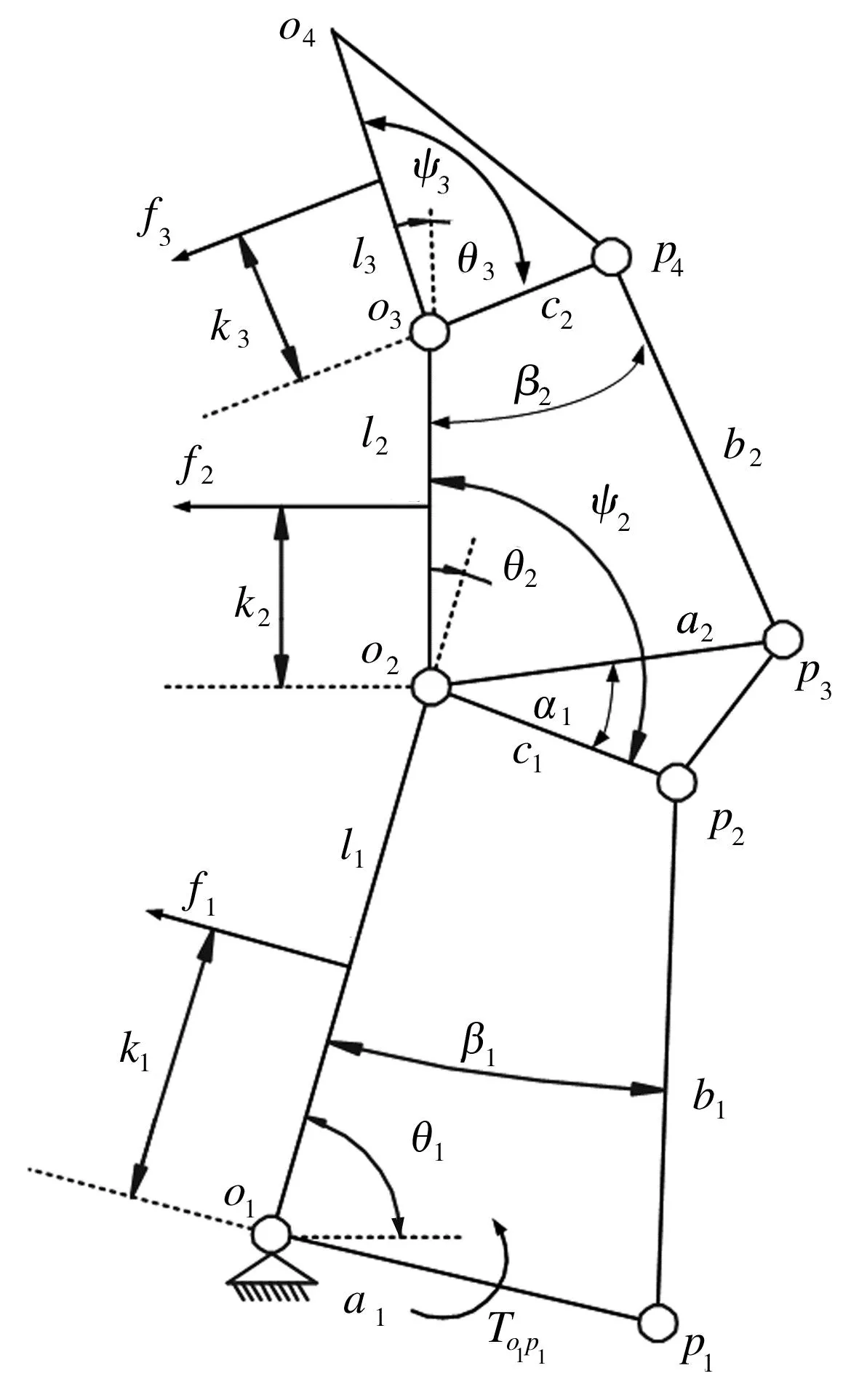
图4 包络抓取接触力模型

分析单指机构在静态工况下的接触力,由虚功原理可知:

tTω=fTv

(2)

式中:t为手指各关节输入力矩向量,ω为各关节对应的角速度向量,f为各关节与抓取物的接触力向量,v为抓取物与各关节接触点处速度沿垂直于指节方向的投影所组成的向量。上述向量参数的具体表达式为:

(3)

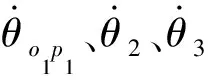
(4)

式中:θ1、θ2、θ3分别为近指节、中指节和指尖的关节转角,l1、l2、l3分别为近指节、中指节和指尖的长度,k1、k2、k3分别为抓取物与近指节、中指节和指尖的接触点到对应销轴的垂直距离。

式(4)可改写为式(5):

(5)

Jm=

(6)

为了表达方便且简洁,将手指结构分成两个四连杆机构,即o1o2p2p1和o2o3p4p3。在四连杆o1o2p2p1中,由三心定理可得:

(7)

式中:d2为点o2到直线o1o2与直线p1p2交点的距离。d2的计算公式为:

d2=c1[cos(θ2-ψ2)-sin(θ2-ψ2)cotβ1]

(8)

其中

(9)

(10)

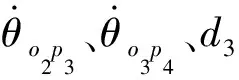
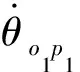
(11)

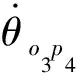
式(11)可以改写成:

(12)

式中:转换矩阵Jn的表达式为

(13)

由式(2)～式(13)得到关节驱动力矩与指节接触力向量f之间的关系为

(14)

综上所述,可得手指全包络状态下接触力f的表达式为

(15)

其中,Q=k2k3d3+k2k3l2-d2k3l2cosθ2+d2d3l2cosθ2cosθ3-d2d3k2cos(θ2+θ3)。

3 单指尺度综合

在连杆式欠驱动灵巧手的单指中,各关节在接触点处的接触力直接影响抓取过程的稳定性和可靠性。为了使单指能稳定而精准地抓取物体,在机构构型确定后,需要对手指进行尺度综合。

3.1 单指结构设计变量

基于所建立的包络抓取接触力数学模型进行优化设计。首先,设定单指关节的长度l1、l2、l3,参考人手指的统计数据,人手指各关节的长度比约为1.25∶1∶0.8,结合抓取的实际需要确定单指的各关节长度l1=45 mm、l2=30 mm、l3=24 mm。其次,基于单指抓取过程的稳定性要求来设定关节转角范围为70°≤θ1≤120°、0°≤θ2≤90°、0°≤θ3≤90°,考虑到包络抓取半径35 mm的球体时关节转角θ2=45°、θ3=40°,暂设驱动力To1p1=1 000 N·mm。综上,单指优化设计的优化变量定义为:X=[x1x2x3x4x5x6]=[a1b1c1a2b2c2]

3.2 目标函数

1)刚性的欠驱动灵巧手抓取形状较大的刚性物体时,手指各关节需要较大的抓取力。因此,为了确保施加在单指3个关节上的接触力总和最大,将优化目标函数1设为:

F1=min(-(f1+f2+f3))

(16)

2)为了满足欠驱动灵巧手在抓取过程中的稳定性,手指应满足力的各向同性[18],使施加在单指3个关节上的接触力之间的差异最小,因此优化目标函数2设为:

F2=min[(f-f1)2+(f-f2)2+(f-f3)2]

(17)

式中:f=f1+f2+f3。

3.3 约束条件

1)单指优化设计变量的取值范围见表1。

表1 手指设计变量的取值范围

2)为使手指具有良好的力传递性能,四连杆机构应满足传动角约束,四连杆机构的传动角变化范围设为(40°,130°),即

(18)

3.4 优化过程及结果

根据优化目标及优化变量的个数,采用多目标遗传算法求解。使用MATLAB中的NSGA-II优化工具箱,初始参数设为:种群大小200、交叉概率 0.8、变异概率0.01、Pareto集的比例0.35、最大迭代次数200。优化后的Pareto前沿如图5所示。

图5 Pareto前沿

因为多目标遗传算法中Pareto前沿是一个最优解的集合,所以本文在选取最优设计参数时,将得到的两个优化目标的数值相加并进行降序排列,然后取其中间值。为减少单次优化导致的误差,一共运行程序10次,选取10次优化的平均值作为最终的优化结果,如表2所示。

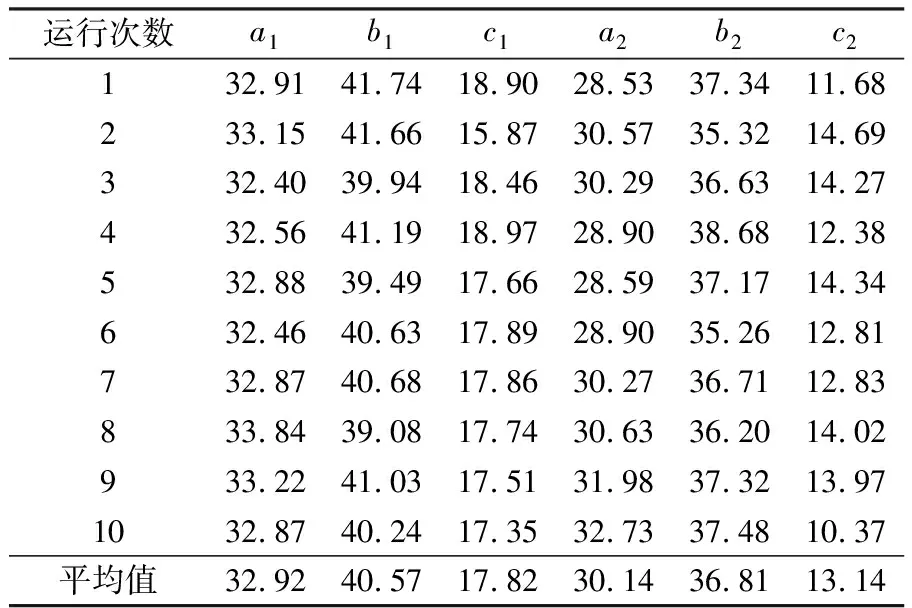
表2 设计参数优化结果(单位:mm)

由表2可见,每次优化结果的数据差别不大。将10次优化结果的平均值圆整后带入到目标函数中求得f1=11.75 N,f2=12.10 N,f3=12.08 N,f=35.93 N。从计算结果来看,在三指节所受力之和尽可能大的情况下其各自受力的差值在可以接受的范围内,符合受力均匀性的要求。

3.5 优化后的单指计算实例

鉴于抓取物的复杂形状和多尺度,即使输入相同的驱动力,手指各指节上的接触力大小也不同。将上述单指优化参数代入接触力模型中进行数值计算,得到单指机构各指节的接触力与指节转角的关系,见图6。

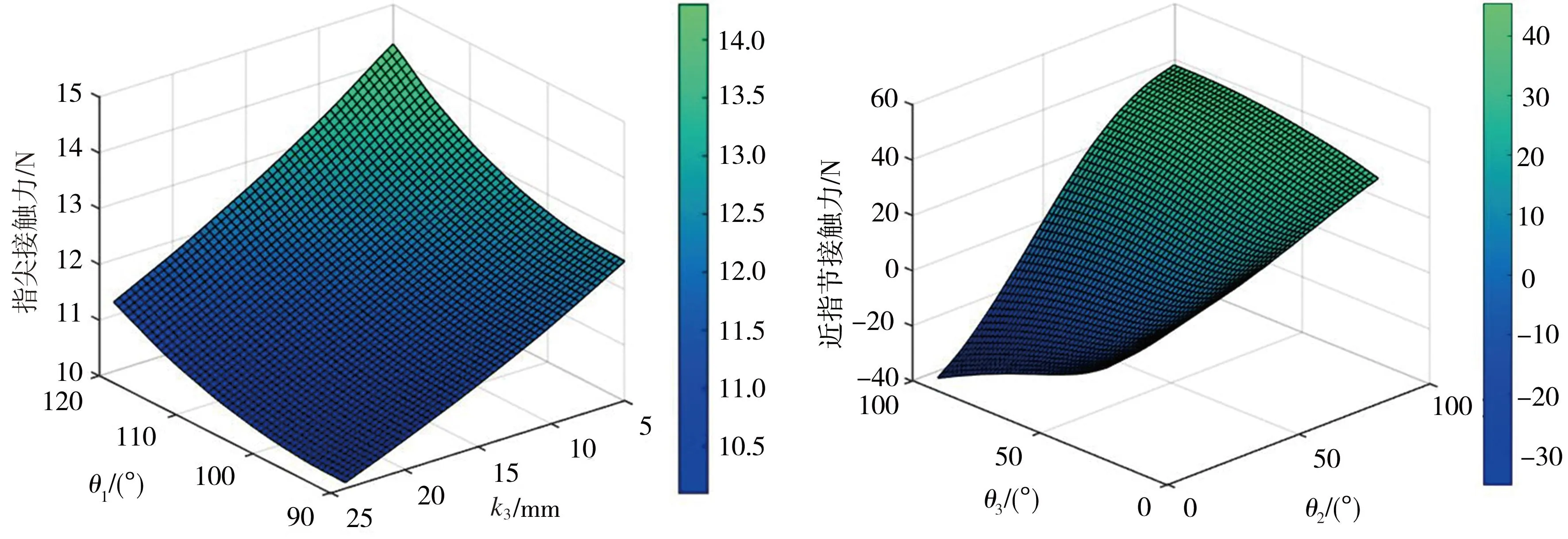
(a)指尖抓取接触力 (b)包络抓取近指节接触力

在To1p1=1000 N·mm、l1=45 mm、l2=30 mm的条件下,指尖抓取接触力的变化如图6(a)所示,显然,接触力随关节转角θ1的增加而增大。此外,指尖接触点离关节销轴的距离k3值越小,指尖上接触力越大,即物体离手掌越近,接触力越大,这符合人手抓取物体的情况,表明该设计是合理的。

在To1p1=1000 N·mm、k1=22.5 mm、k2=15 mm、k3=12 mm的情况下,包络抓取各指节的接触力变化如图6(b)～图6(d)所示。由图6(b)可见,当手指关节转角θ2<35°且θ3>35°时,近指节接触力会出现负值,导致弹射失稳现象[19],故在包络抓取时应避开这一区域;由图6(c)可见,当关节转角θ2固定时,中指节接触力随着关节转角θ3的增加而增大,这是因为远指节开始承受接触力时,中指节包络更紧以便于抓住物体;由图6(d)可见,当关节转角θ2固定时,远指节接触力随着关节转角θ3的增加而增大,这符合人手抓取物体的情况,表明该设计是合理的。

4 动力学仿真

4.1 单指结构设计

灵巧手单指机构的三维模型见图7,每个手指由手指安装支架、电机、传动系统、3个指节和3个拉伸弹簧组成,单指有3个关节,通过弹簧设计使得手指具有自适应抓取能力。每个手指使用单独的电机驱动,可实现单指模块化,便于更换手指以满足不同的任务需求。

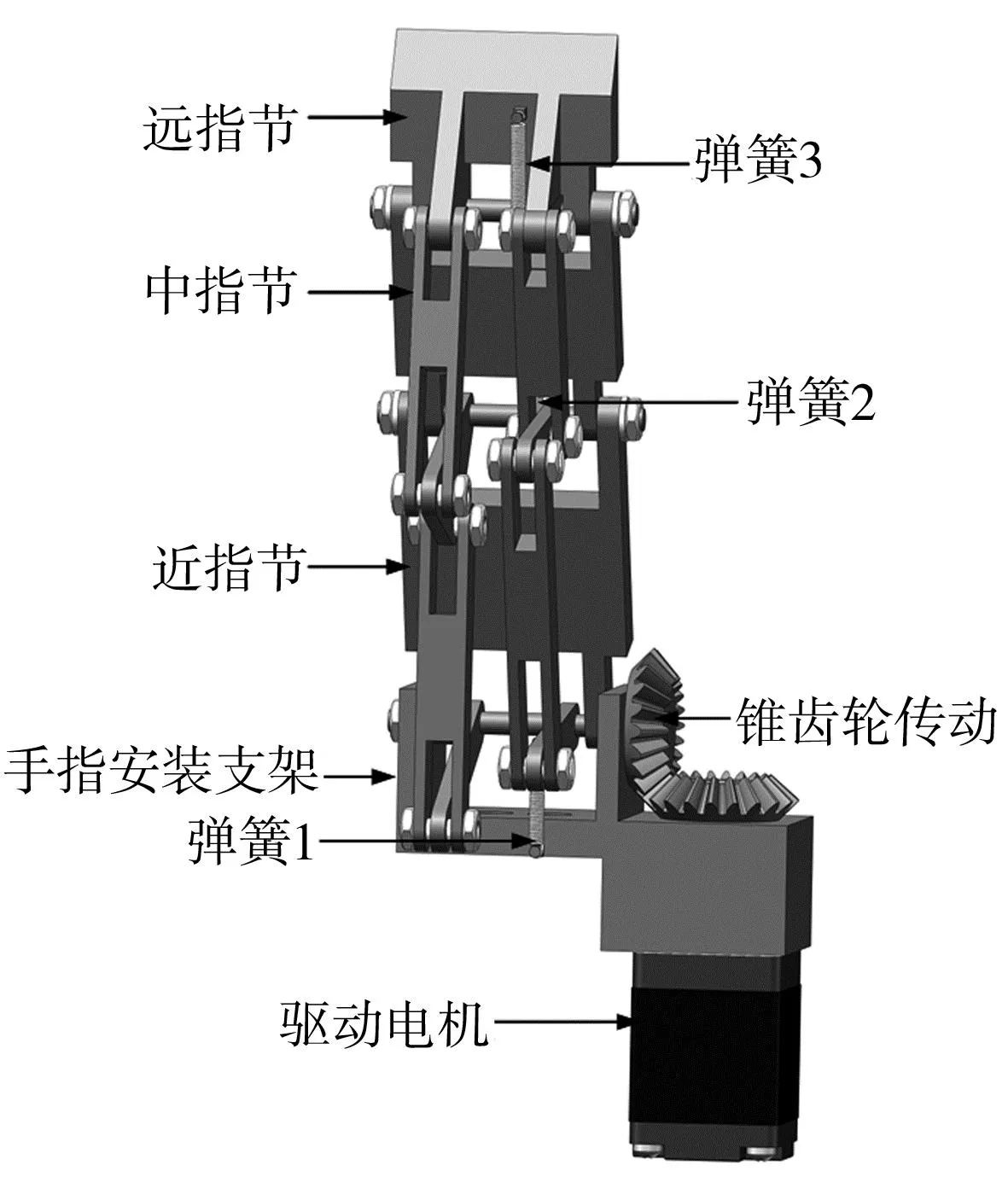
图7 单指机构的三维模型

4.2 欠驱动灵巧手的整体设计

欠驱动灵巧手的整体结构设计见图8(a),一共有10个自由度、4个驱动装置。该机构有3个手指,采用可变手掌协同手指抓取的方式来设计两个转动手指,转位范围见图8(b),可实现两指对心抓取、三指平行抓取以及三指对心抓取。在设计阶段综合考虑手指与手掌尺寸的相互耦合,使手掌长度与手指长度的比例满足0.4～0.6[20]。手指机构的长度设为99 mm,则手掌机构的尺寸范围是39.6～59.4 mm,考虑到抓取大物体的情况,将手掌尺寸定为59 mm。通过以上设计,扩充了欠驱动灵巧手对不同形状、不同尺寸的抓取物的适应范围。

(a)灵巧手整体机构 (b)灵巧手转位范围

4.3 抓取实验

为了进一步验证欠驱动灵巧手的设计合理性,使用ADAMS软件进行抓取仿真实验。首先,将建立好的三维模型导入ADAMS中,添加运动副、接触力等约束,使用弹簧对杆件进行连接,并添加驱动函数step(time,0,0.5,1000)。其中,弹簧1的刚度系数为1 N/mm,弹簧2的刚度系数为0.7 N/mm,弹簧3的刚度系数为1.2 N/mm。

对不同形状多尺寸的物体进行抓取实验,具体见图9。图9(a)～图9(c)所示为欠驱动灵巧手抓取不同大小的球体,验证了手指与手掌耦合设计尺寸的合理性;图9(a)～图9(f)表明灵巧手对不同形状、不同尺寸的抓取物具有良好的适应性;图9(g)和图9(h)验证了指尖抓取的稳定性。

(a)三指包络抓取小球体 (b)三指包络抓取中球体 (c)三指包络抓取大球体 (d)三指包络抓取三角板

包络抓取半径为35 mm的球体时(图9(a)),各指节的接触力大小如图10所示,可以看到,3个指节上的接触力相差不大,满足优化目标。参考公式(15),代入优化后的尺度参数,3个关节接触位置分别为k1=22.5 mm、k2=15 mm、k3=12 mm,关节转角θ2=45°、θ3=40°,计算得到近指节f1=11.75 N,中指节f2=12.08 N,远指节f3=12.10 N。接触力理论值与仿真结果基本一致,略有差异的原因是理论分析时忽略了弹性元件阻尼力。

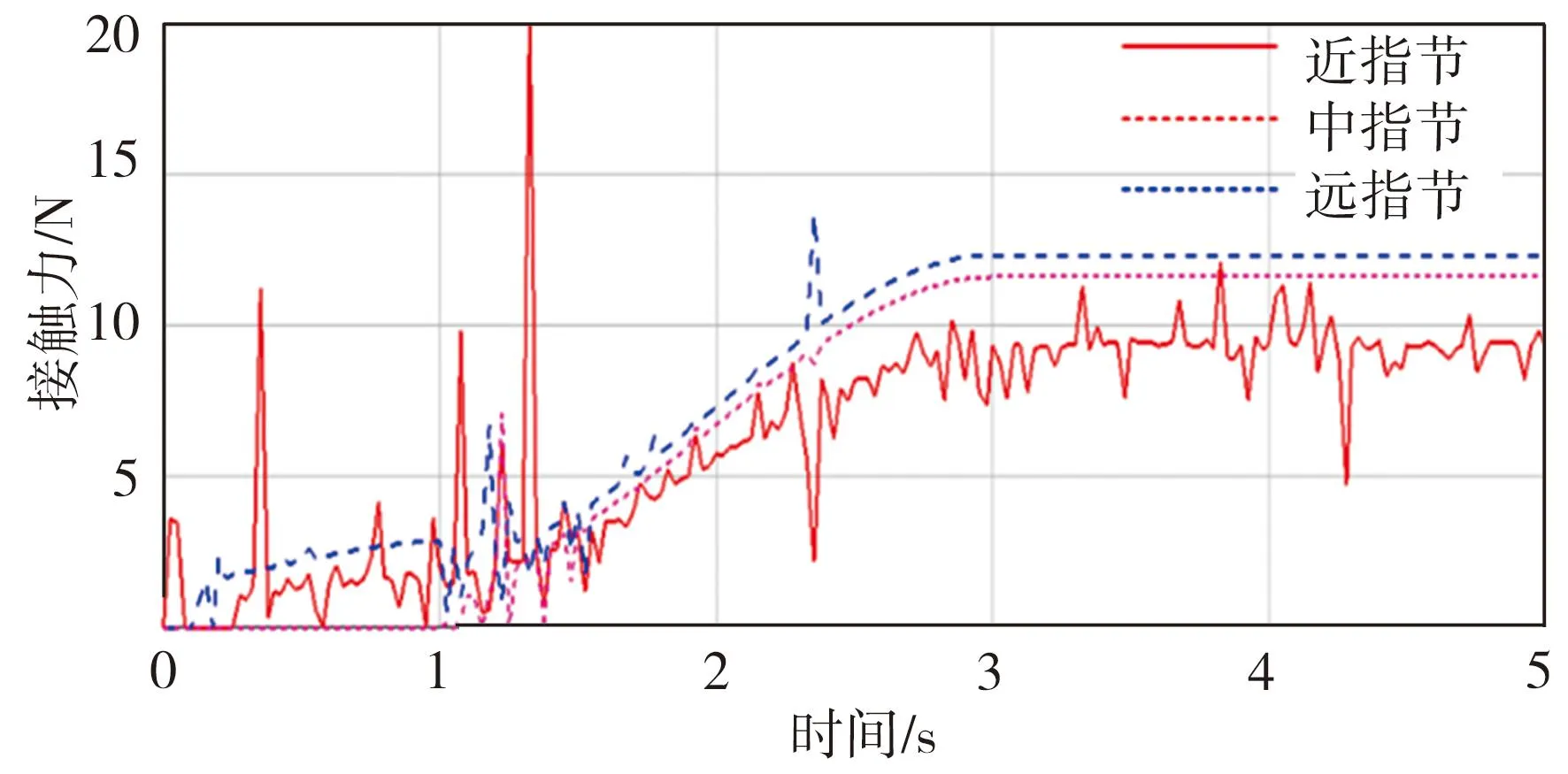
图10 包络抓取小球体时3个指节的接触力

包络抓取长度120 mm、半径40 mm的棒材时(图9(e)),各指节的接触力大小如图11所示。参考公式(15),代入优化后的尺度参数,接触位置k1=28.08 mm、k2=17.38 mm、k3=14.25 mm,关节转角θ2=38.39°、θ3=37.99°,近指节f1=4.76 N,中指节f2=7.01 N,远指节f3=10.76 N。接触力理论值与仿真结果基本一致。

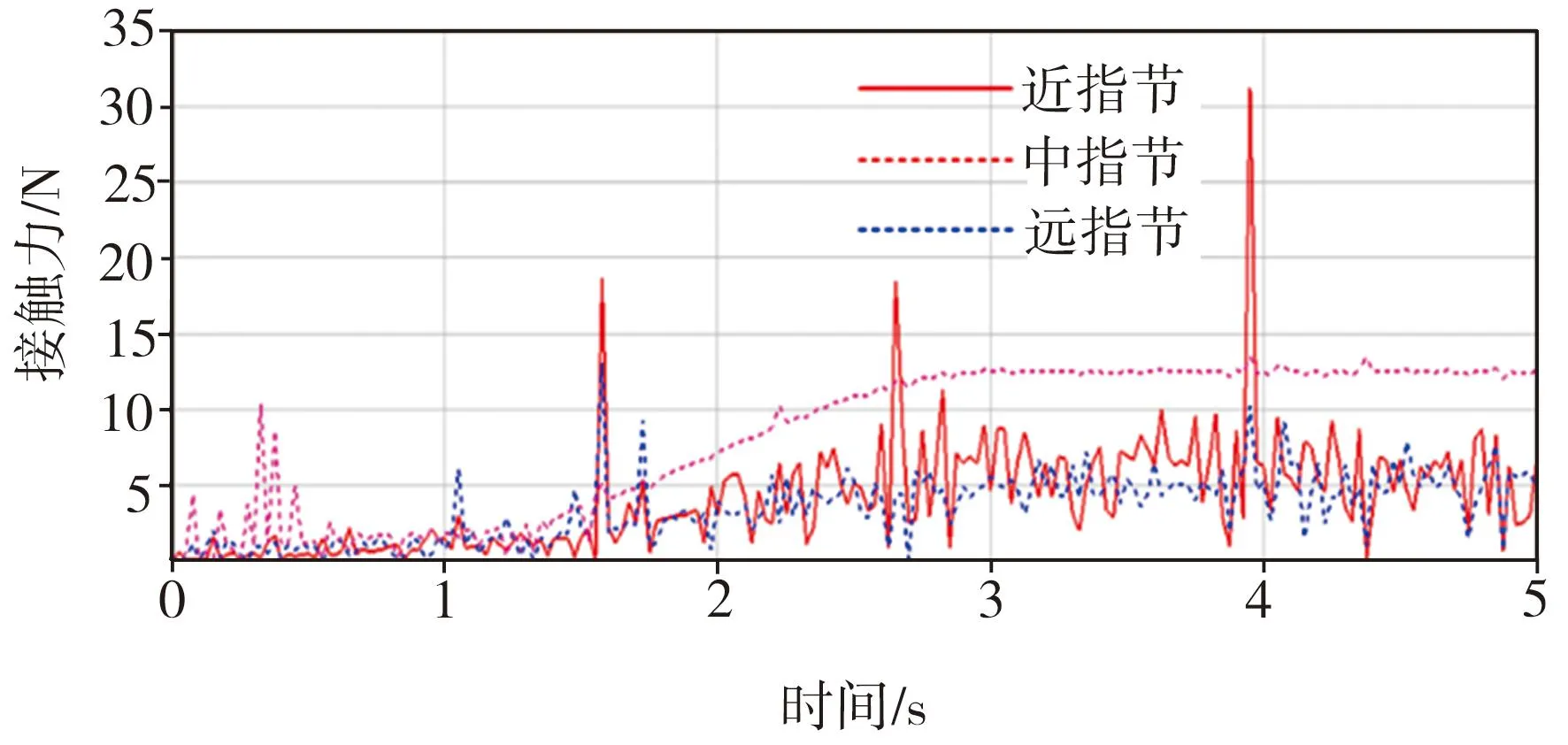
图11 包络抓取棒材时3个指节的接触力

指尖抓取长度50 mm、宽度30 mm、高度15 mm的长方体时(图9(g)),各指节的接触力大小如图12所示。当指尖与抓取物接触时会产生碰撞,因此在0～3 s期间接触力逐渐上升,3～5 s时灵巧手运动达到稳态,此时指尖接触位置k1=6.24 mm、关节转角θ1=91.5°。将优化后的尺度参数代入公式(1),得到指尖接触力的理论值为12.31 N,与仿真结果基本一致。

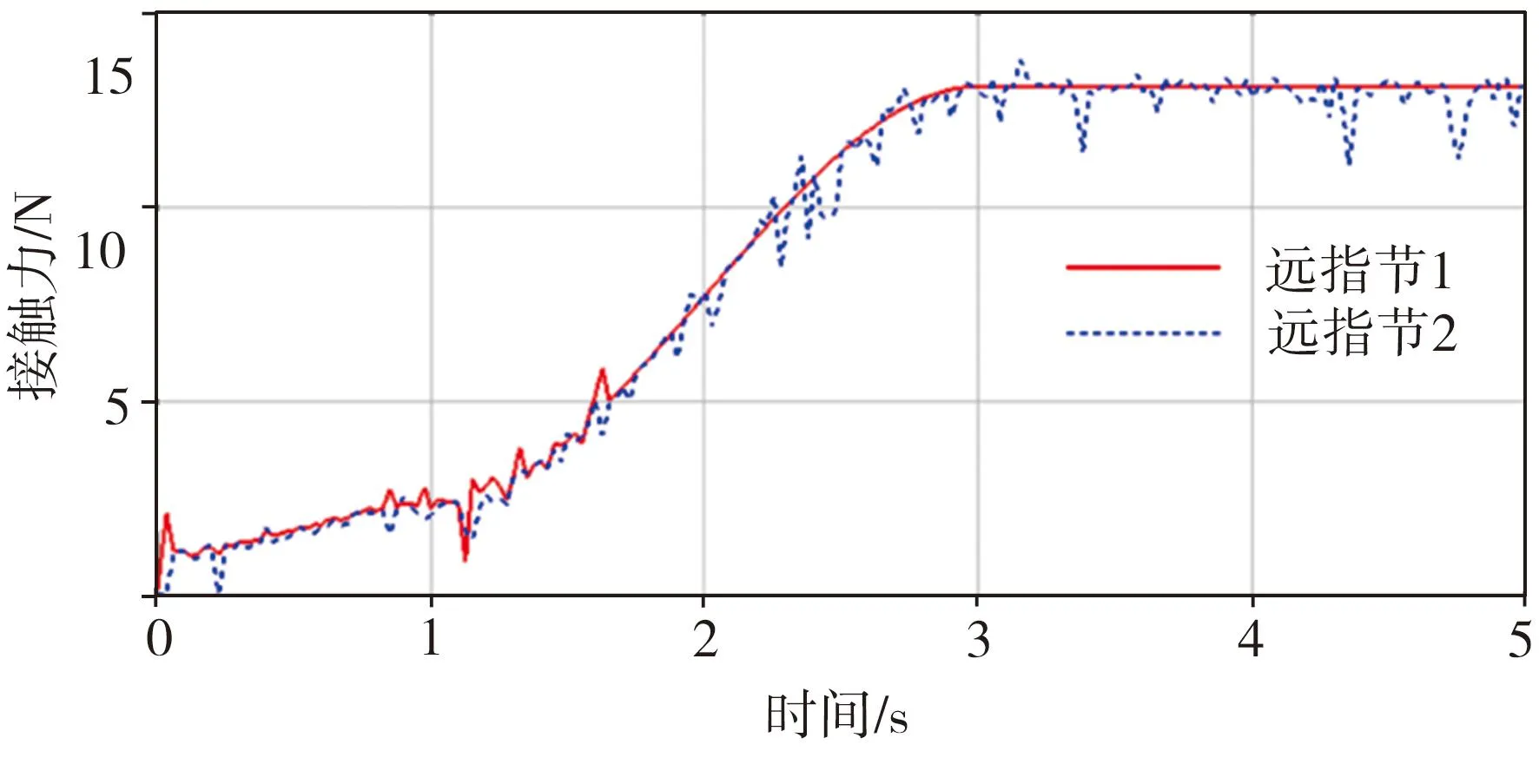
图12 两指指尖抓取长方体时的接触力

5 结语

本文基于协同耦合设计思路,设计了一种欠驱动灵巧手机构,建立了单指机构的接触力模型并对手指机构进行尺度综合,讨论了单指机构及灵巧手整体的结构设计。同时利用ADAMS软件进行抓取仿真实验,分析了每个关节在抓取不同物体时的接触力,抓取实验结果验证了本文设计的合理性。该灵巧手可实现两指对心抓取、三指平行抓取以及三指对心抓取,能稳定抓取不同大小和形状的物体。