双稳态压电-电磁复合俘能器非线性动力学分析
2024-01-16倪祥禄陈定方李立杰
梅 杰,倪祥禄,宋 钢,陈定方,李立杰
(1.武汉理工大学智能制造与控制研究所,湖北 武汉,430063; 2.武汉理工大学交通与物流工程学院,湖北 武汉,430063; 3.英国斯旺西大学工程学院,英国 斯旺西,SA1 8EN)
振动俘能器是将来自环境的振动能量转换为电能的装置,根据能量转换机理的不同,其主要分为四类,即基于压电效应的压电式俘能器、基于电磁感应的电磁式俘能器、基于电容原理的静电式俘能器以及摩擦式俘能器。单一能量转换方式的效率较低,将两种或两种以上的能量转换方式集中使用则可以提高俘能效果,故复合俘能器已逐步成为微能源研究的主要方向。另外,传统的线性能量采集器具有较高的谐振频率,当环境频率偏离谐振频率时,系统的发电性能将急剧下降,因此线性能量采集器的环境适应性较差[1]。非线性系统复杂的动力学行为[2-4]为拓宽振动俘能器的工作频带、提高俘能效率提供了新思路,越来越多的学者引入具有非线性刚度特征的结构以构成具有非线性单稳态和双稳态特性的振动俘能器[5-8]。2009年,Challa等[9]首次设计了一种悬臂梁式的压电-电磁复合振动俘能器,通过实验测得其总输出功率为340 μW,该装置是一种简单的复合俘能器,为后续研究奠定了基础。Kim等[10]研发了一种新型的双稳态复合振动俘能器,该装置由悬臂梁和一对相互排斥的磁体组成,一个磁体连接在自由端,另一个连接到与悬臂梁轴向对齐的线性弹簧形成弹簧加载的磁体振荡器。这种结构降低了双阱势垒,实现了悬臂梁在低激励振幅和频率下的阱间振荡。Yao等[11]研究了一种新型双稳态压电-电磁俘能器的发电和非线性动力学行为,设计了三种不同类型的压电悬臂梁结构,包括单稳态压电悬臂梁、双稳态弹簧-磁体压电悬臂梁以及双稳态弹簧-磁体-线圈压电悬臂梁,并对每种结构的发电效率和动态特性进行了实验研究,结果表明双稳态压电-电磁俘能器具有最佳性能。
本文以能够承受长期振动疲劳的聚偏氟乙烯(PVDF)为压电材料,提出一种双稳态悬臂梁式压电-电磁复合俘能器结构。考虑梁的几何非线性应变,并引入磁力势能建立复合俘能器模型,继而研究激励频率、磁铁间距和负载电阻等参数对系统输出的影响,然后进行俘能器的非线性动力学分析和整流滤波分析。
1 压电-电磁复合俘能器建模及稳定性分析
1.1 复合俘能器几何模型
本文研究的压电-电磁复合俘能器装置如图1所示,能量转换包括压电部分和电磁部分。悬臂梁由一层钢基底材料和一层 PVDF 压电材料组成,在悬臂梁末端固定有动磁铁A,动磁铁右边相隔一定距离处有一个静磁铁B,在动磁铁下方放置有感应线圈。压电层通过可忽略厚度的平面电极与负载电阻R1相连接;感应线圈两端连接有负载电阻R2。在基础激励的作用下,悬臂梁发生振动,运动形式随着激励频率和幅值的不同而变化。
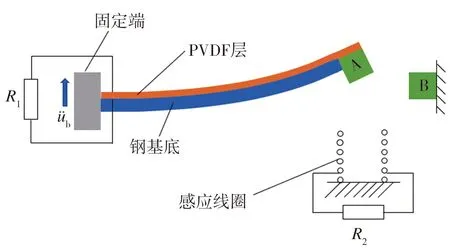
图1 压电-电磁复合俘能器示意图
由于所设计的悬臂梁长宽比较大,故主要考虑梁横向振动引起的变形。应力方向垂直于电场方向,所以该结构满足第二类压电本构方程,压电本构关系为
(1)

压电层内,电场强度为
(2)
式中:V(t)为压电层的总输出电压,其中t代表时间;hp为PVDF厚度。
根据Euler-Bernoulli梁理论,大变形时应变和位移之间的关系可以表示为
S1=
(3)
式中:w(x,t)为悬臂梁纵向坐标x处相对于基座的横向位移,z为悬臂梁横截面上某处到中性层的距离。
悬臂梁截面几何尺寸如图2所示。基底和PVDF压电层的厚度分别为hs和hp,两层宽度均为b,h3为PVDF层顶部距中性层的距离,h2为PVDF层底部距中性层的距离;h1为钢基底的底部距中性层的距离。
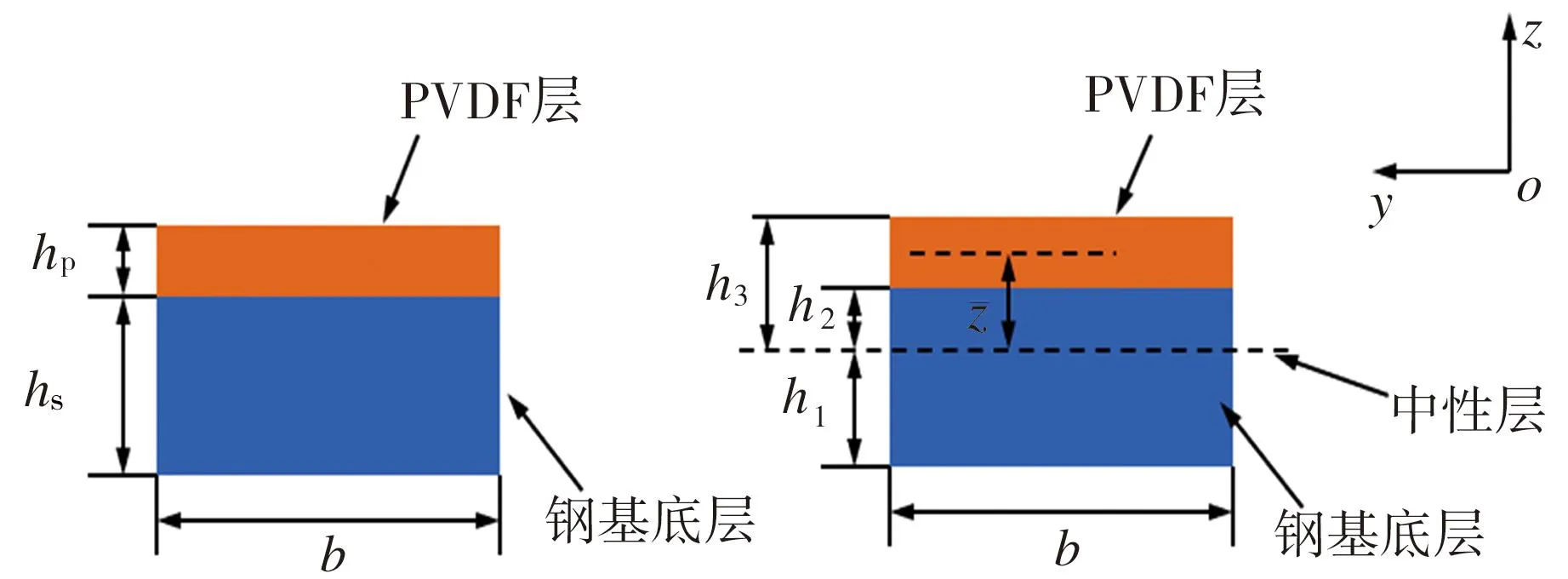
图2 悬臂梁截面几何尺寸
中性层位置参考文献[12]中的方法确定,有下式成立:
(4)
式中:Ys为钢基底的杨氏模量。由式(4)可解得中性层距离PVDF层和钢基底层的距离:
(5)
悬臂梁复合弯曲刚度YI可表示为
(6)
式中:Is、Ip分别为钢基底层和PVDF层相对于中性层的惯性矩。
1.2 复合俘能器非线性动力学建模
将复合俘能器的末端磁铁看作质点,不考虑其转动惯量。压电-电磁复合俘能器的机电耦合模型如图3所示,其中,w为压电振子相对于基座的位移,ub为位移激励。

图3 压电-电磁复合俘能器的机电耦合模型
根据Hamilton原理,建立在外界激励下系统的多物理场耦合压电-电磁复合俘能器分布式参数模型:
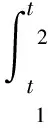
(7)
式中:δ代表变分符号,T为系统动能,U为系统弹性势能,We为系统电势能,Wm为电磁能,Um为磁力势能,δWnc为虚功的变分。
系统的动能包括悬臂梁和末端磁铁的平动动能,可表示为
(8)
式中:(·)代表函数对时间的导数;L为悬臂梁长度;m为单位长度悬臂梁的质量,m=ρsAs+ρpAp,其中ρs、ρp分别为钢基底和PVDF压电材料的密度,As、Ap分别为钢基底层和PVDF层的横截面积;Mt为末端磁铁质量。
系统的弹性势能包括压电悬臂梁内部与应变相关的势能,可表示为
(9)
式中:T1为悬臂梁的应变,S1为悬臂梁的应力,Vs为钢基底层体积,Vp为PVDF层体积。

(10)
压电-电磁复合俘能器的电磁机电耦合系数θe是一个关键参数。电磁感应原理如图4所示,其中标明了线圈与动磁铁的几何位置关系,根据文献[13]可得到电磁机电耦合系数θe:
(11)
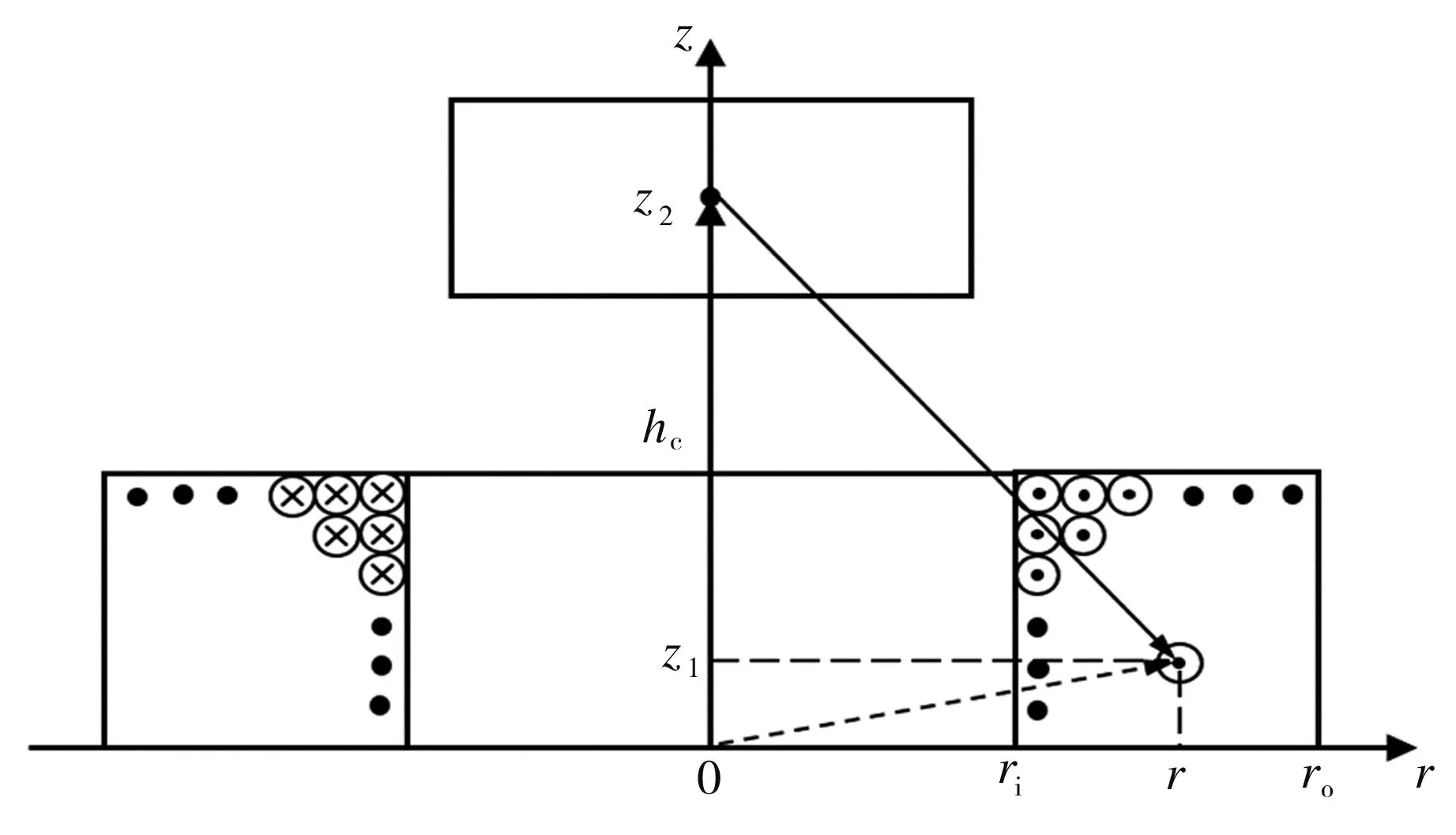
图4 电磁感应原理图

由式(11)可知电磁机电耦合系数与磁铁的位置有关。为了方便分析,通常取磁铁静止时的值作为恒定值进行研究,即θe=θe(z0)。
系统的电磁能为线圈自有的磁共能,可以表示为
(12)
式中:Lc为感应线圈的电感。线圈电感可利用Wheeler公式计算:
(13)
式中:ra为线圈的平均半径,ra=(ri+ro)/2。
在电荷输出和机械阻尼效应作用下,虚功的变分可以表示为
δWnc=-Qp(t)Up(t)-
(14)
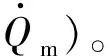
对于内、外半径分别为ri、ro,高为hc的空心螺线管,其电阻为
Rc=2πraNρc
(15)
式中:ρc为漆包线单位长度电阻值。
根据Galerkin法将横向位移函数w(x,t)分解成N个振形函数和N个模态坐标的乘积:

(16)
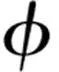
根据Euler-Bernoulli梁理论,振形函数可以设为
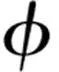
Cnsin(knx)+Dnsinh(knx)
(17)
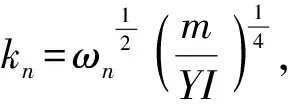
对于有末端质量块的悬臂梁,将质量块视为一个质点,则其边界条件和正交性可表示为
(18)
式中:δns代表Kronecker符号。
由于一阶振型对输出的影响最大,这里只考虑一阶振型,因此横向位移可以写为
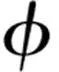
(19)
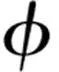
磁力势能由梁端部的运动磁铁A和外部静止磁铁B相互作用产生,其几何关系如图5所示。图中,mA=(-MAVAsinα,MAVAcosα),mB=(0,MBVB),其中MA、MB分别为磁铁A和磁铁B的磁化强度,VA、VB分别为磁铁A和磁铁B的体积。
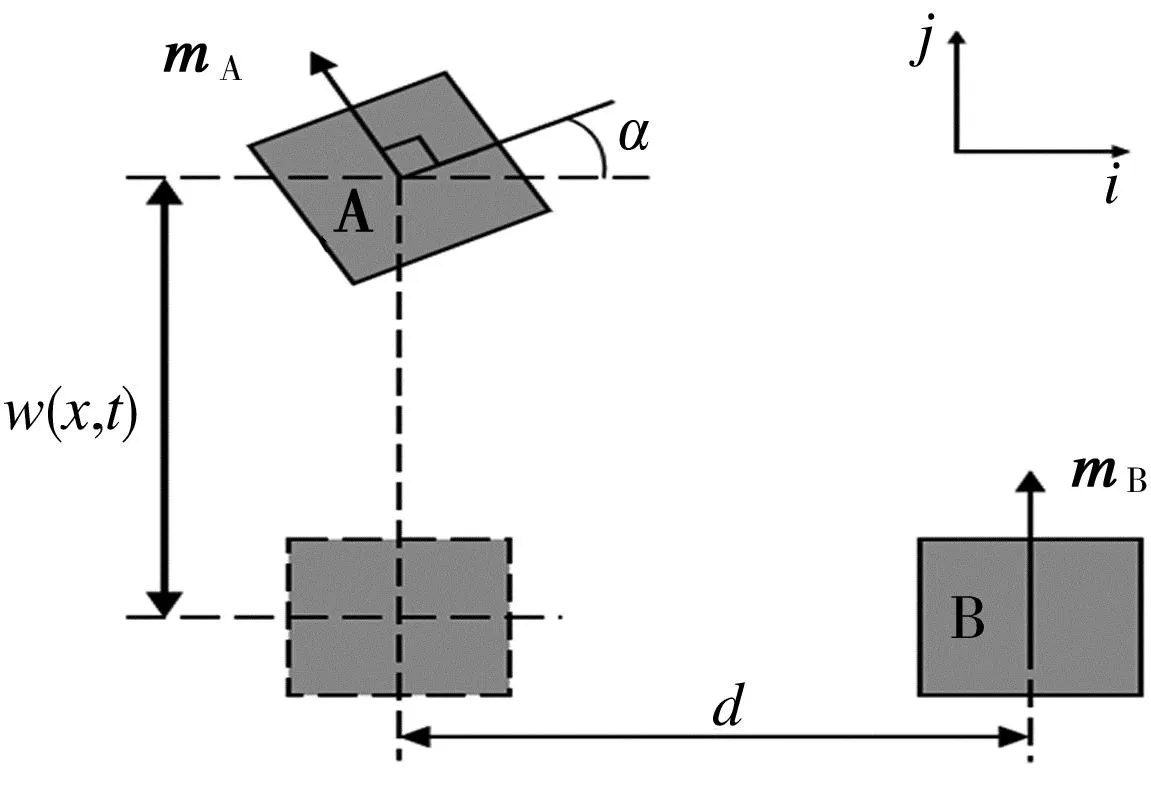
图5 磁场模型
根据磁偶极子模型可知磁场强度表达式为
(20)
式中:rBA=(-d,w)。
磁力势能可以表示为
(21)
其中,
(22)
(23)
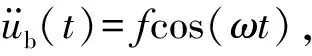
系统动能变分为
(24)
弹性势能变分为
(25)
电势能变分为

(26)
式中:Cp为等效电容。
电磁能变分为
(27)
虚功变分为
(28)
磁力势能变分为
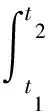
(29)
将上面各部分变分代入式(7),由于η(t)、Qm(t)、Qp(t)为独立变量,故可分离变量得到:
(30)
(31)
(32)
其中,
(33)
(34)
(35)
(36)
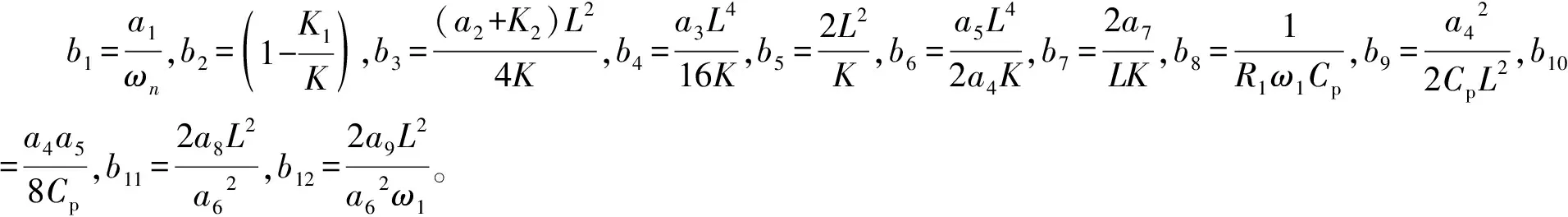
假设悬臂梁式压电-电磁复合俘能器的动力学解为
(37)
可以得到上式中各阶次和高次项的表达式:
(38)
式(38)中:H.O.H代表高次谐波项,在后续计算中将其忽略。
将式(37)和式(38)代入式(34)~式(36)中,平衡谐波项和常数项的系数,可以得到:
-b6S(A1A2+B1B2)=0
(39)
(40)
(41)
(42)
(43)
(44)
(45)
(46)

同样,式(42)~式(45)可以写为
(47)
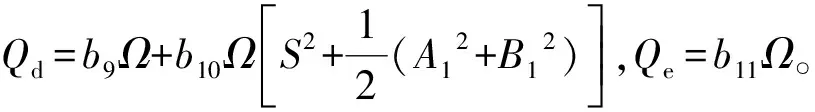
通过式(47)可以得到压电和电磁部分的稳态解析解为
(48)
将上述稳态解带入式(46),可以得到振幅方程的稳态解:
(49)

结合式(48)化简,可以得到无量纲化的压电电压、电磁感应电流和总功率表达式为
(50)
对式(39)进行整理可得:
(51)
由式(51)可以得到关于S的两个解。
1)当S=0时,系统处于阱间运动;
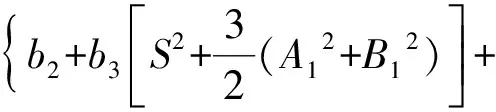
分别将S的两个取值代入运动方程中,可以得到关于振幅的隐函数,求解后可以分别得到阱内运动和阱间运动状态下的位移幅值。将式(48)代入式(50),可以求得压电电压、电磁感应电流和总功率的幅值。
1.3 复合俘能器稳定性判定
前面对振幅求解时可以得到多个解,其中可能包含不稳定解,因此需要对解的稳定性进行分析。

然后将式(39)~式(45)改写成为非自治系统的形式,可以得到:
(52)
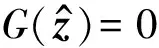
(53)
如果该矩阵所有特征值的实部均小于零,则可认为此平衡点是稳定的,否则便是不稳定的。
2 压电-电磁复合俘能器仿真分析
根据上节分析结果,本节运用MATLAB软件针对悬臂梁式压电-电磁复合俘能器的动力学模型进行输出性能仿真分析,探讨激励振幅、激励频率、磁铁间距和负载电阻对系统输出性能的影响。仿真中的材料参数见表1。

表1 压电-电磁复合俘能器材料参数
2.1 系统双稳态分析
为了研究动磁铁和静磁铁的间距d对系统双稳态的影响规律,利用数值计算方法得到d不同时系统无量纲刚度(b2,b3)和无量纲势能的变化曲线,如图6和图7所示。由图可知:

图6 系统无量纲刚度(b2,b3)与磁距d的关系曲线
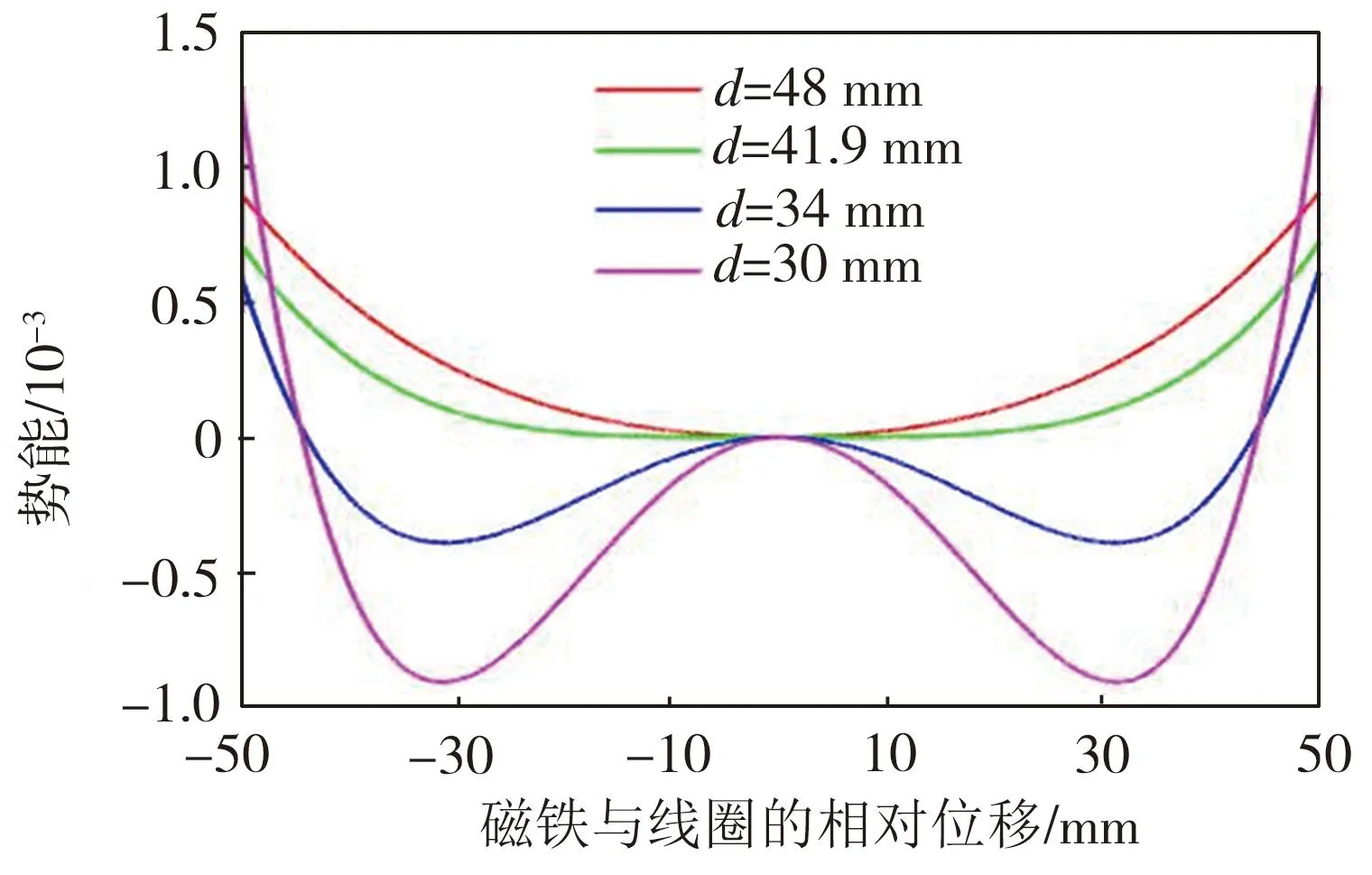
图7 不同磁距d时的系统势能变化曲线
1)当d=41.9 mm时,系统线性刚度为0,因此可以将d=41.9 mm看作判断系统是否呈现双稳态的分岔点:d<41.9 mm时,系统表现为双稳态;d>41.9 mm时,系统表现为单稳态渐硬特性。
2)随着磁距d的减小,势垒高度和两势阱间的幅度都在增大。这说明磁距越小,系统越过势垒所需要的能量就越大。
3)当磁距d合适时,系统有足够能量越过势垒,这时存在两个明显的势阱,系统表现出双稳态运动行为,系统的振动位移幅值得到提高。
2.2 激励幅值对俘能特性的影响
设置负载电阻为R1=16.5 MΩ、R2=600 Ω;通过改变激励加速度f来调节激励幅值,f分别取1、3、5、8 m/s2。4种激励下,压电电压输出幅值和电磁电流输出幅值随频率比Ω的变化如图8和图9所示,其中实线部分代表经Jacobi矩阵分析得到的稳定解,而虚线代表不稳定解。可以看出,随着激励频率的不断增加,阱间运动的压电输出电压和电磁输出电流的幅值在逐渐增大,直到激励频率超出频带宽度后,系统便落入势阱中开始做阱内运动。
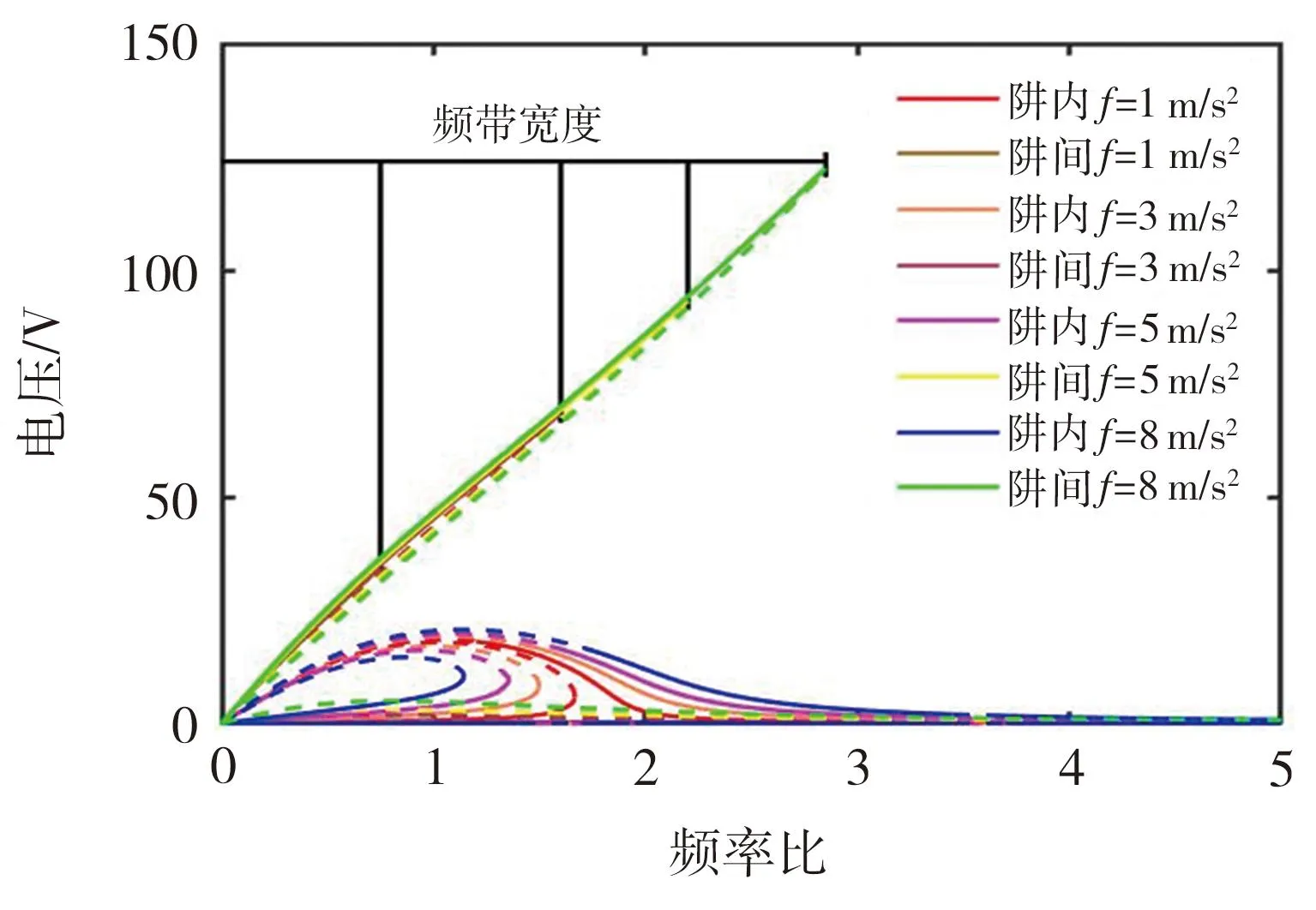
图8 不同激励加速度下的压电输出电压响应曲线

图9 不同激励加速度下的电磁输出电流响应曲线
由图8和图9还可以发现,激励加速度的增大明显拓宽了系统阱间运动的工作频带范围。激励加速度从1 m/s2增至8 m/s2,阱间运动带宽从0.75倍的固有频率增大到了2.85倍的固有频率,但是激励加速度的增大对阱内运动的频带范围影响很小。并且,同样的激励加速度增幅会明显提高阱间运动的压电输出电压和电磁输出电流,但对阱内运动的输出影响很小。
2.3 磁铁间距对俘能特性的影响
设置激励加速度为3 m/s2,负载电阻为R1=16.5 MΩ、R2=600 Ω,动磁铁和静磁铁间的初始距离分别取32、34、36、38 mm。分析磁铁间距对系统输出的影响,如图10和图11所示,图中实线和虚线同样分别代表稳定解和不稳定解。
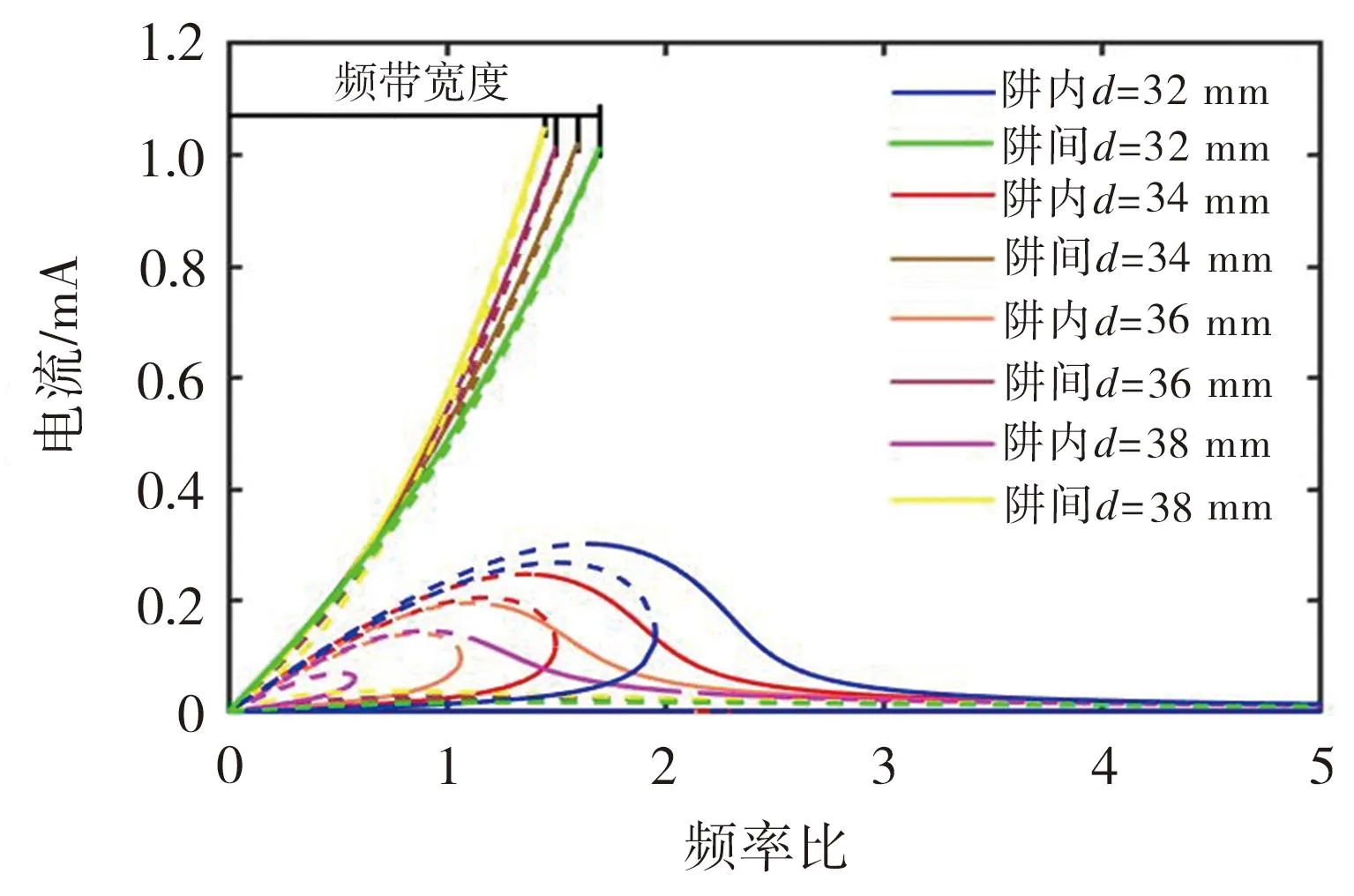
图11 不同磁铁间距下的电磁输出电流响应曲线
从图10可以看出,随着磁铁间距的增大,在阱内运动状态下,压电部分最大输出电压所对应的频率会逐渐减小,同时稳态解范围会扩大。对于阱间运动来说,随着磁铁间距的增大,频率带宽会有所减小,但系统的最大压电输出电压会有所提高。从图11可以看出,磁铁间距以相同幅度改变对电磁部分在阱间状态下的输出没有明显影响,但在阱内运动状态下,电磁部分最大输出电流所对应的频率会逐渐减小,同时稳态解范围会扩大。
2.4 负载电阻对俘能特性的影响
由上述分析可知,系统的最大输出是在阱间运动状态下出现的,所以本小节以阱间运动为对象进行研究。分别取压电电阻R1为1、5、10、16.5、30、50、70 MΩ,电磁电阻R2为50、100、400、600、1000、2000 Ω,相应的系统输出如图12~图15所示。
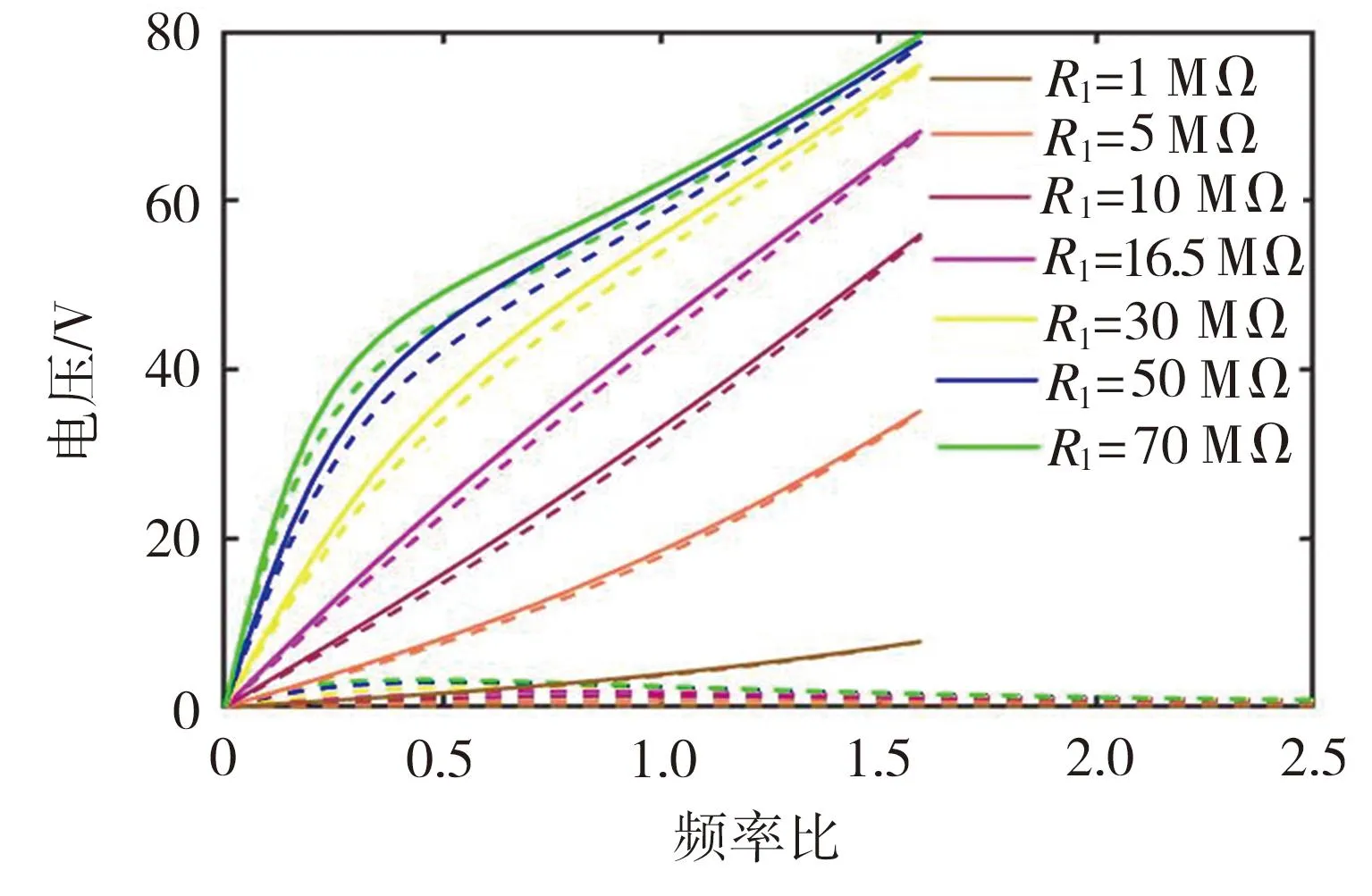
图12 不同压电负载下的压电输出电压响应曲线

图13 不同压电负载下的压电输出功率响应曲线

图14 不同电磁负载下的电磁输出电流响应曲线
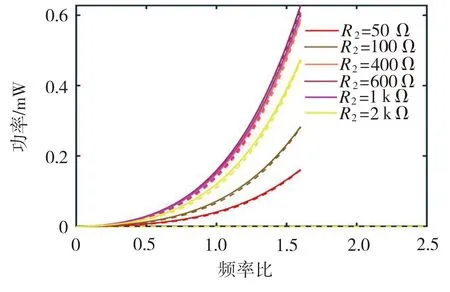
图15 不同电磁负载下的电磁输出功率响应曲线
从图12~图15可以看出:随着负载的增大,压电俘能部分和电磁俘能部分的输出功率都呈现出先增大后减小的变化规律;压电输出电压随着压电负载的增大而升高,电磁输出电流随着电磁负载的增大而降低。同时发现,不论是压电负载还是电磁负载发生变化时,阱间运动的频率带宽基本保持不变,均为1.6倍的固有频率。
系统总输出是压电俘能部分和电磁俘能部分的累计。由于阱间运动的带宽不会随着负载而改变,因此保持其他参数不变,取频率比为1.6,分析系统的最优负载。图16所示为俘能器在压电负载和电磁负载同时变化时的系统总输出功率P。可以看出:当压电负载一定、电磁负载从100 Ω增至1200 Ω时,总输出功率先逐渐增大然后略微减小;当电磁负载一定、压电负载电阻从0.01 MΩ增至1000 MΩ时,总输出功率呈现先增大后减小的变化趋势;总输出功率随压电负载的变化幅度比其随电磁负载的变化幅度要大得多。在压电负载为10 MΩ、电磁负载为680 Ω时,系统的总输出功率达到最大,为0.9449 mW。

图16 总输出功率随压电、电磁负载的变化
系统在阱间运动状态下、激励加速度为3 m/s2、频率比为最优值1.6时,压电部分输出电压/功率和电磁部分输出电流/功率随负载的变化情况分别如图17和图18所示。由图17可见,随着电阻R1的增大,压电部分输出电压逐渐增大,但R1>10 MΩ后,电压不再明显增长,同时压电部分输出功率的变化也在该负载值处出现拐点,呈现下降趋势。因此,系统的最优压电负载为10 MΩ,对应的最大压电输出功率为0.3145 mW。由图18可见,随着电阻R2的增大,电磁部分功率也呈现出先增大后减小的变化趋势,R2=680 Ω时出现拐点,对应的电磁部分最大输出功率为0.6304 mW。另外,电磁电流随负载的增大呈现出缓慢减小的变化趋势。

图17 压电输出电压/功率随压电负载的变化

图18 电磁输出电流/功率随电磁负载的变化
图19为系统在阱间运动状态下、电磁负载取最优值(680 Ω)时,压电输出功率和电磁输出功率的占比随压电负载的变化情况。可以看出,随着压电负载的增加,压电输出功率占比先增大后减小,当压电负载为10 MΩ时,压电输出功率占比达到最大(33.28%),此时电磁输出功率占比达到最小(66.72%)。

图19 输出功率占比随压电负载的变化
图20为系统在阱间运动状态下、压电负载取最优值(10 MΩ)时,压电输出功率和电磁输出功率的占比随电磁负载的变化情况。可以看出,随着电磁负载的增大,电磁输出功率占比先增大后减小,在电磁负载大于680 Ω后,电磁输出占比和压电输出占比的变化趋缓。与图19相对应,当电磁负载为680 Ω时,电磁输出功率占比达到最大(66.72%),压电输出功率占比最小(33.28%)。

图20 输出功率占比随电磁负载的变化
3 压电-电磁复合俘能器非线性动力学分析
本文研究的复合俘能器属于非线性系统。一般非线性系统具有多种复杂的运动,如混沌运动、倍周期运动等。本节运用MATLAB中的龙格-库塔法进行求解,分析激励改变对俘能器动力学行为的影响。
图21为悬臂梁式压电-电磁复合俘能器的系统分岔图。可以看到,随着激励加速度的增大,悬臂梁表现出丰富的非线性特性。可大致分为以下几个阶段:当激励加速度f在0~5.5 m/s2范围内时,悬臂梁振动处于周期运动状态;当f在5.5~7.6 m/s2范围内时,悬臂梁振动处于周期运动与混沌运动的交替变化中,且前面部分主要表现为混沌运动状态,后面部分主要表现为周期运动状态;当f在7.6~8.9 m/s2以及9.45~10 m/s2范围内时,悬臂梁处于混沌运动状态;当f在8.9~9.45 m/s2范围内时,悬臂梁处于周期运动状态。

图21 压电-电磁复合俘能器的系统分岔图
选取f为1、6.15、9.1、9.6 m/s2四种情况进行运动分析。图22~图25所示为不同激励条件下系统的动态响应。f为1 m/s2和9.1 m/s2时,悬臂梁均处于周期运动状态,压电输出和电磁输出均为周期性变化。其中,f=1 m/s2时,系统处于单周期运动;f=9.1 m/s2时,系统处于五倍周期运动;同时,随着激励增强,时域波形图的幅值也在增大。当f为6.15 m/s2和9.6 m/s2时,悬臂梁进入混沌运动状态,此时压电输出电压和电磁输出电流均不稳定。
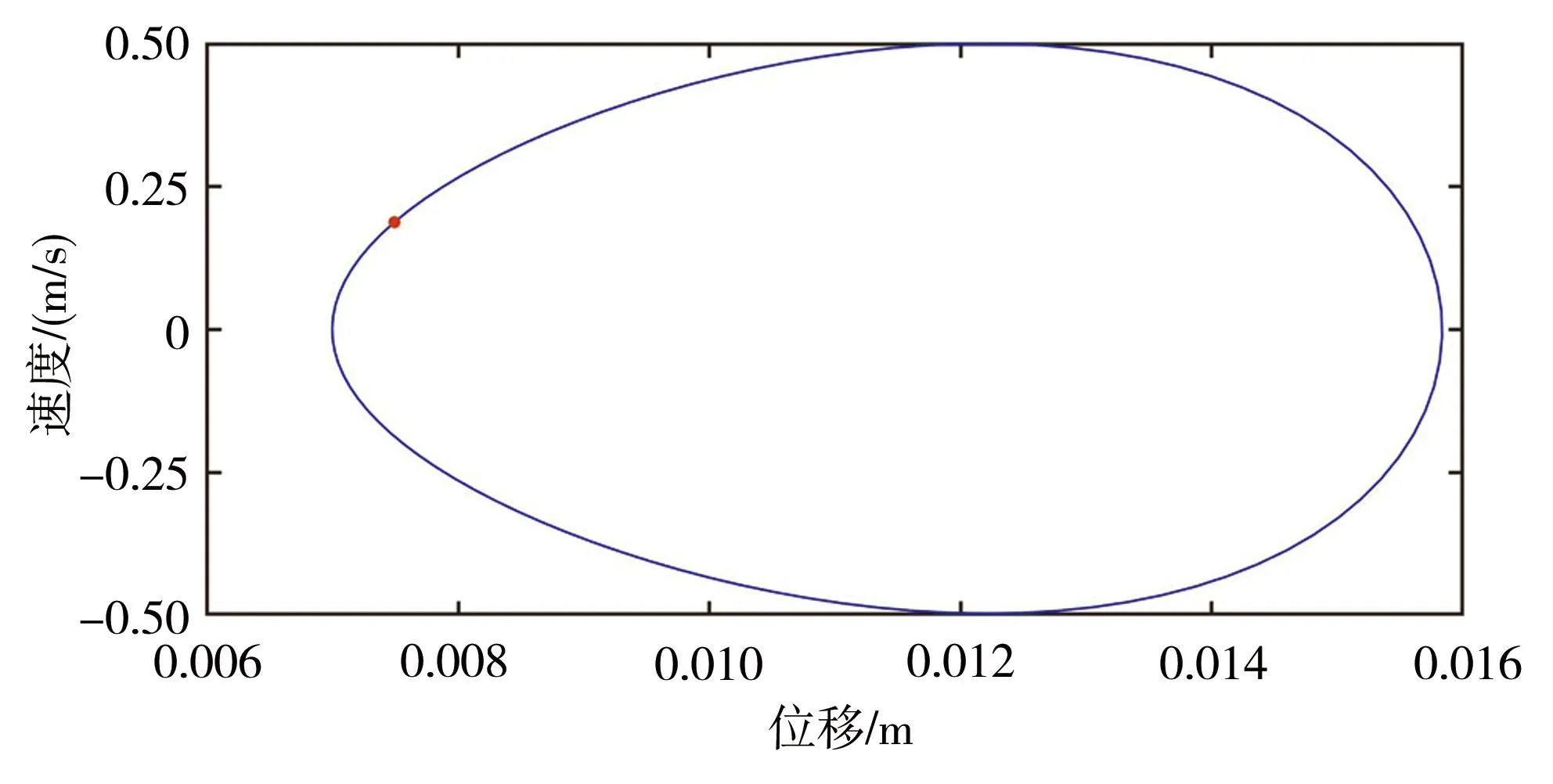
(a)位移-速度相图及庞加莱截面
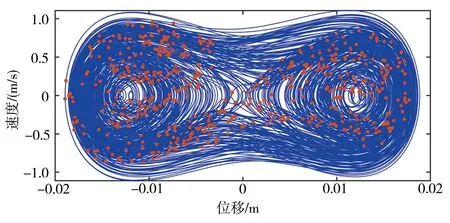
(a)位移-速度相图及庞加莱截面

(a)位移-速度相图及庞加莱截面
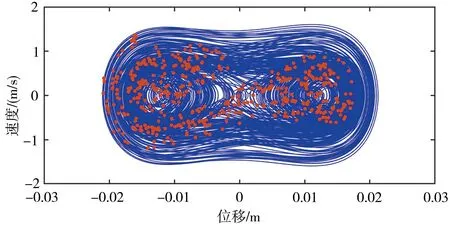
(a)位移-速度相图及庞加莱截面
从上面的分析可以得知,悬臂梁式压电-电磁复合俘能器系统在激励幅值不断增大时会产生周期运动和混沌运动的交替变化,并且压电输出电压和电磁输出电流具有相同的变化情况。也就是说,相图显示为周期运动时,压电输出和电磁输出均发生周期性变化,相图显示为混沌运动时,压电输出和电磁输出均处于不稳定的变化状态。
4 压电-电磁复合俘能器电路仿真分析
本节采用Multisim电路仿真软件对系统在上述不同激励条件下的输出进行整流滤波分析。首先建立压电部分和电磁部分的等效电路模型。通常前者等效为一个电流源、后者等效为一个电压源,分别如图26(a)和图27(a)所示。图26(b)和图27(b)分别为压电和电磁整流滤波电路。

(a)压电等效电路图 (b)压电整流滤波电路
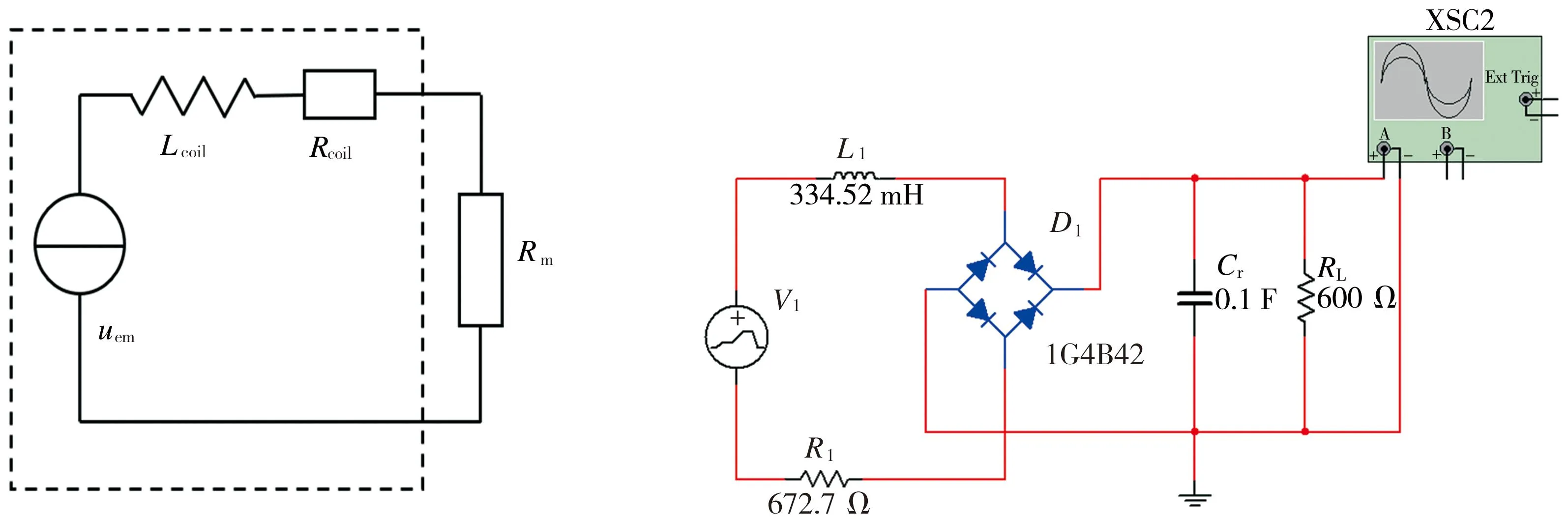
(a)电磁等效电路图 (b)电磁整流滤波电路
取激励加速度为1 m/s2和6.15 m/s2时的输出进行分析,结果见图28~图29。激励加速度为1 m/s2时,改变电路的滤波电容,压电和电磁整流滤波后的输出都可以达到稳定状态,并且电容越大,达到稳定状态所需时间越长,同时稳定状态时的波动越小。例如在图28中,当电容Cr=10 μF,系统大概在680 s时达到稳态;当电容Cr=15 μF,系统大概在850 s才能达到稳态。但是,激励加速度为6.15 m/s2时,采用同样大小的滤波电容,经过整流滤波后,压电和电磁输出仍然表现出大幅无规则波动。
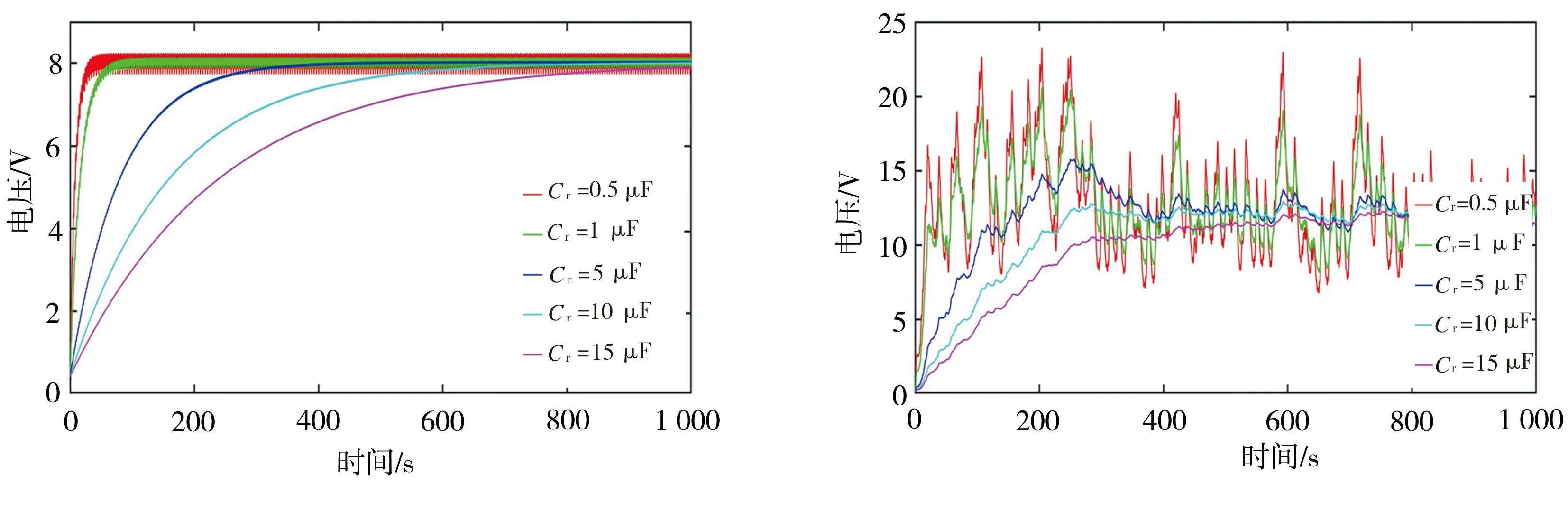
(a) f=1 m/s2 (b)f=6.15 m/s2
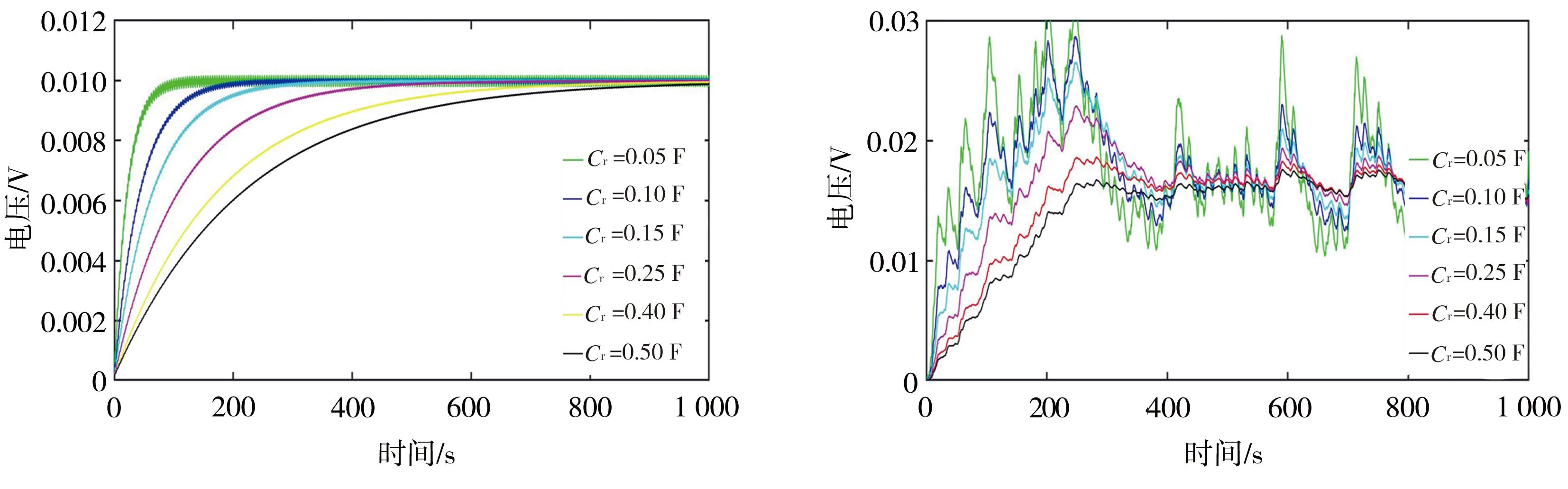
(a) f=1 m/s2 (b)f=6.15 m/s2
由以上分析可知,当悬臂梁系统处于周期运动时,不管是电磁输出还是压电输出,在经过整流滤波后都可以达到一个相对稳定的输出状态。只是滤波电容越大,稳定状态时的波动越小,但到达稳定所需的时间越长。系统处于混沌运动时,系统输出无法通过标准整流电路和滤波电容进行整流滤波而达到稳定状态。
5 结论
本文提出了一种双稳态悬臂梁压电-电磁复合俘能器结构,基于Euler-Bernoulli梁理论和Hamilton原理建立系统的非线性动力学模型,利用谐波平衡法进行求解;通过MATLAB仿真分析了激励幅值、激励频率、磁铁间距和负载电阻对俘能器输出性能的影响,然后运用龙格-库塔法进行系统非线性动力学分析;最后采用Multisim软件进行整流滤波分析。研究得到如下结论:
1)对于具有几何非线性结构的俘能器,随着激励幅值的增大,阱间运动的频率带宽增大。磁铁间距的改变对阱间运动的带宽影响不大。负载电阻的变化不会影响系统阱间运动的频率带宽。
2)通过电阻扫描可以知道,系统存在一组最优负载使得输出的总功率达到最大。本文系统的最优压电负载为10 MΩ,最优电磁负载为680 Ω。此时系统俘获的总功率达到最大值0.9449 mW。
3)随着激励的增强,系统在混沌运动状态和周期运动状态间相互转换。在周期运动状态时,可以利用标准整流滤波电路进行能量采集;在混沌运动状态时,标准整流滤波电路无法稳定收集系统能量输出。
