吹氩模式对钢包内多相流流动行为影响的数值模拟研究
2024-01-16秦绪锋王凤良程常桂
秦绪锋,王凤良,程常桂,李 阳,卫 卫,金 焱
(1.武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室,湖北 武汉,430081;2.武汉科技大学钢铁冶金新工艺湖北省重点实验室,湖北 武汉,430081;3.无锡巨力重工股份有限公司,江苏 无锡,214111)
炉外精炼是提升钢液质量和钢材品级的关键环节,钢包底吹氩作为其中应用最广泛的一种手段,其通过在钢包底部设置透气元件吹入氩气形成气泡羽流,对熔池内钢液进行搅拌,起到均匀钢液温度和成分、促进夹杂物上浮和钢渣界面反应的作用[1-4]。然而,吹氩形成的气泡羽流会降低熔池顶部渣层的稳定性,导致钢液卷渣和吸氧增氮[5-6],甚至会加速钢包内衬耐火材料熔损,影响钢包的使用安全性。
对底吹氩钢包内流体运动特性已有大量研究,通过调整吹氩点数目和位置、改变透气元件类型等方式来改善钢包内多相流的流动结构,提升搅拌和精炼效率[7-8]。Owusu等[9]采用粒子图像测速仪和图像处理技术,研究了不同类型透气元件对钢包冶金效果的影响,发现多孔透气砖产生的气泡羽流能提供更强烈的对流和湍动能,这与其产生尺寸均匀的小气泡有关。卢寅寅等[10]通过水力学模型分析了圆孔型透气砖与狭缝式透气砖的冶炼效果对比,结果表明,圆孔斜通透气砖在混匀时间、夹杂物去除率和渣眼面积控制方面表现更优。Ramasetti等[11]在考虑气泡间相互作用的基础上,通过数值模拟方式研究了单孔和双孔吹氩下钢包内钢渣流动行为,发现大容量钢包采用双孔吹氩可获得更好的搅拌效果。近期有研究发现,采用双孔差流量吹氩的方式更有利于钢液混匀和渣层裸露面积减少[12-14]。这些研究对于理解和改善底吹氩工艺和提高钢液洁净度具有重要意义,但其未能进一步分析熔池内流体结构对壁面的影响。
实际生产中,底吹氩所形成的气泡羽流在促进流体流动的同时,会加快钢渣对钢包内衬的化学腐蚀,并加剧流体对钢包耐材的流动侵蚀[15],导致钢包内衬损毁,并产生大量外源夹杂物,显著降低钢水纯净度和钢材的机械性能[16]。这与钢液流动引发的壁面剪应力和温度分布有关[17-18]。Huang等[19]研究发现,底吹氩条件下钢包内渣线位置的侵蚀率较高,随着吹氩流量增大,耐材侵蚀速度加快,但关于侵蚀位置与流动的相关性尚不明晰。Wang等[20]通过构建瞬态三维流固耦合模型,模拟钢包内氩气-钢液-保护渣的三相流动行为,发现靠近透气砖一侧的渣线位置侵蚀率明显超过其他部位,这与此处上升气泡羽流所产生的强烈剪切流有关。由此可见,虽然底吹氩在精炼过程中发挥着重要作用,但同时也会对钢包内耐火材料产生不利影响[21]。在提高钢铁产能、降低能耗比的背景下,通过优化底吹氩钢包流场,减缓耐材侵蚀损耗以减少耐材使用、提高钢包容积,对于实现钢包轻量化也具有重要意义。
基于此,本文通过耦合流体体积(VOF)方法与离散相模型(DPM),计算钢包内气泡运动和钢渣两相界面波动,模拟底吹氩钢包内的多相流流动,分析了不同底吹氩模式(单孔吹氩、双孔等流量吹氩和双孔差流量吹氩)对钢包内流场、钢渣界面行为和壁面剪应力分布的影响,以期为优化钢包底吹氩工艺和提升钢液质量提供理论依据。
1 数学模型
1.1 钢包几何结构
本文以某钢厂150 t钢包为研究对象,钢包的几何结构如图1所示。钢包高度、底部和顶部有效直径依次为3 635、2 733、3 488 mm。钢包采用弥散型透气砖吹氩,单孔吹氩和双孔吹氩的透气砖布置见图1(b)和1(c),透气砖顶面直径为80 mm,其距钢包中心点沿X轴和Y轴方向的距离分别为500、550 mm。钢包液位高度为2 600 mm,液渣层厚度为150 mm。
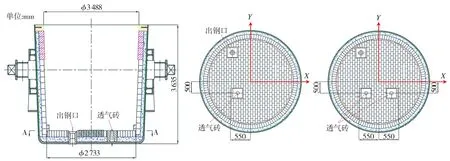
(a)主视图 (b)俯视图,单孔吹氩 (c)俯视图,双孔吹氩
1.2 基本假设
对所建模型作如下假设:①钢液和保护渣为牛顿不可压缩流体,其物性参数均为常数;②不考虑传热和化学反应对流体流动的影响;③不考虑空气层、粉渣层和烧结层对钢渣界面的影响;④气泡为球形,气泡尺寸符合Rosin-Rammler分布。
1.3 控制方程
在钢渣界面区域,采用VOF模型对非混多相流进行界面追踪。连续性方程和Navier-Stokes方程可表示为:
(1)
·(μl·v)+ρlg+Fσ+Fother
(2)
ρl=αρsteel+(1-α)ρslag
(3)
μl=αμsteel+(1-α)μslag
(4)
上述式中:ρl为流体密度,kg/m3;v为流体速度,m/s;t为时间,s;α为流体体积分数;p为静压力,Pa;μl为流体黏度,Pa·s;g为重力加速度,取9.8 m/s2;ρsteel、ρslag分别为钢液和液渣密度,kg/m3;μsteel、μslag分别为钢液和保护渣黏度,Pa·s;Fσ为钢渣两相界面张力,N/m;Fother表示单位质量气泡离散相对连续相所施加的作用力,N。
采用标准κ-ε湍流模型来求解钢包内气液两相流引起的湍流流动,湍动能κ和湍动能耗散率ε方程分别为:
(5)
(6)
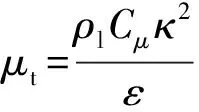
(7)
上述式中:G为由平均速度梯度所产生的湍动能,m2/s2;μt为湍流黏度,Pa·s;C1ε、C2ε、Cμ为经验常数,σκ、σε分别为κ、ε的湍流普朗特数,C1ε、C2ε、Cμ、σκ、σε取值依次为1.44、1.92、0.09、1.0、1.3。
将气泡视为离散相,利用DPM模型追踪气泡在钢渣连续相中的运动行为。气泡所受作用力的平衡方程见式(8),由此可求得气泡的运动轨迹和空间位置分布,即:
(8)
(9)
(10)
上述式中:vb,i为气泡速度,m/s;db,i为气泡直径,m;ρb为气泡密度,kg/m3;Cvm为虚拟质量系数,取0.5;Cd为曳力系数;α1、α2、α3为经验常数;Reb为气泡雷诺数。式(8)右侧分别为气泡受到的曳力、重力和浮力,以及压力梯度力和虚拟质量力之和。
为准确预测气泡特性对气液两相流流动影响,考虑了气泡间的斯托克斯碰撞聚合,采用O’Rourke算法对气泡间的碰撞进行随机估算,气泡间的碰撞概率Pc可表示为
(11)
式中:r1、r2分别为气泡半径,m;vrel为气泡间相对速度,m/s;Vcell为单元网格体积,m3;Δt为步长,s。
聚并气泡速度vB由下式确定:
(12)
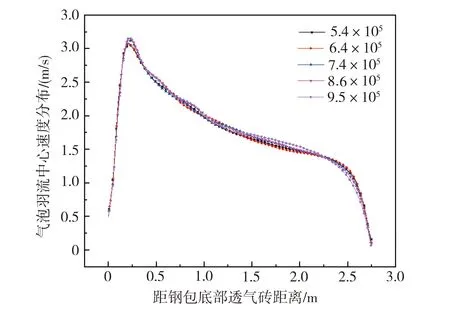
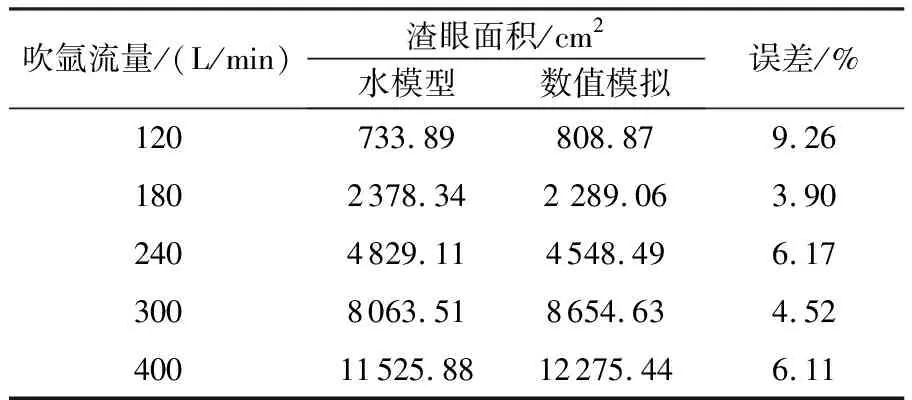
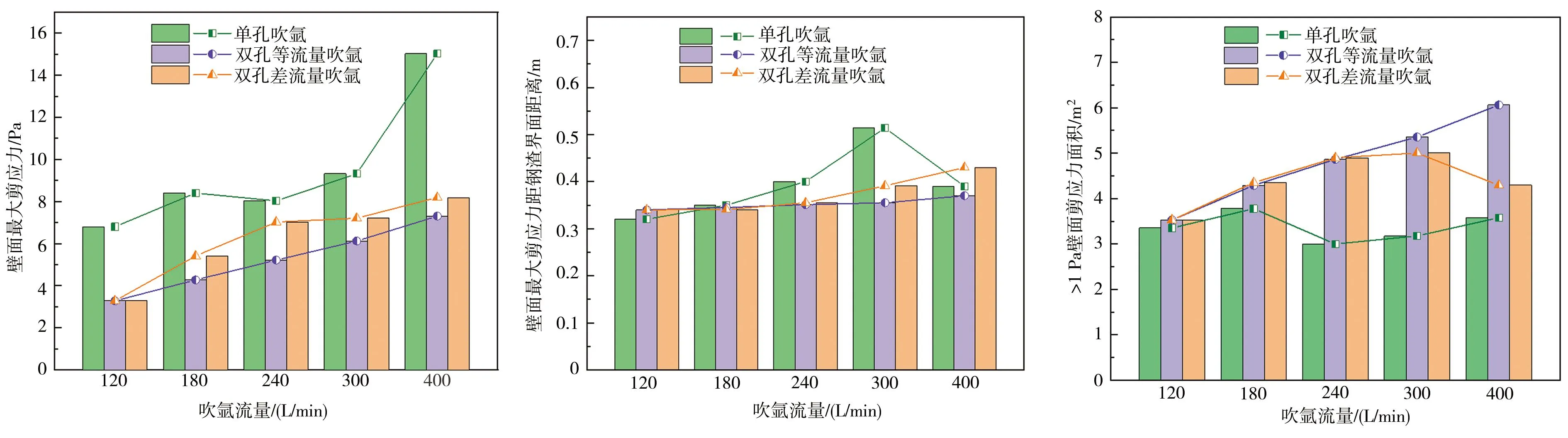
式中:m1、m2为合并前两气泡质量,kg;v1、v2为合并前两气泡速度,m/s;b、bcrit分别为单元格内碰撞气泡实际偏移量和临界偏移量,当b 钢包壁面区域采用标准壁面函数处理,采用无滑移边界条件,氩气泡壁面边界条件为反弹;钢包上表面设置为自由剪切壁面边界条件,氩气泡到达上表面将发生逃逸。求解过程中,采用耦合压力和速度项的Simplec算法和Geo-Reconstruct方法对钢渣界面进行插值并追踪计算,速度项采用二阶迎风格式。计算中,采用0.005 s的步长非稳态计算20 s,得到稳定流场,各参数收敛残差均小于1×10-4。采用ANSYS ICEM对钢包几何模型进行结构网格划分,对速度变化较大的吹氩区域和钢渣界面处进行网格加密处理,其中钢渣界面处初始网格尺寸为5 mm,网格增长率为1.5,网格数目约8.6×105。钢包几何模型和网格划分示意图见图2。数值模拟所用物性参数列于表1中,其中气泡初始尺寸范围为0.2~5.0 mm,气泡平均尺寸为2.5 mm[7]。单孔吹氩(G1)、双孔等流量吹氩(G2)和双孔差流量单孔吹氩(G3)的数值模拟方案如表2所示。 表1 数值模拟用物性参数 表2 实验方案 (a)钢包几何模型 (b)计算网格划分 1.5.1 网格无关性验证 为分析模拟结果与网格数目的相关性,在单孔吹氩、吹氩流量180 L/min条件下,对网格进行整体加密处理,网格数目分别取5.4×105、6.4×105、7.4×105、8.6×105、9.5×105时,计算得到透气砖中心上方沿钢包高度方向的速度分布如图3所示。由图3可知,随着距钢包底部透气砖距离的增加,透气砖上部流体速度呈先增大后减小的趋势,这与底吹氩所形成的气泡羽流分布有关。气体通过透气砖形成大量小气泡,透气砖上部附近的钢液在气泡群浮力作用下快速上浮,速度迅速增大;气泡进一步上浮过程中向四周扩散,单位体积内流体所受浮力作用减弱,上浮速度也随之降低;在靠近熔池液面位置,气泡羽流冲击液渣层后动量衰减并转为表面流动,速度进一步降低。不同网格数量下,流体速度分布计算结果基本一致,未显示出较大的差异性。为减少模型计算工作量,同时保证一定的计算精度,本文采用的网格数目为8.6×105。 图3 不同网格数目下透气砖中心处沿钢包高度方向的速度分布 1.5.2 水模型验证 为进一步验证该数学模型的可靠性,基于相似原理,采用1∶5比例的水模型研究单孔吹氩条件下钢渣界面波动行为。采用Image J软件对水模型实验得到的图片进行处理,利用像素法计算得到渣眼面积大小。当吹氩流量为180 L/min时,由水模型实验和数值模拟计算得到的典型渣眼形态如图4所示,不同吹氩流量下渣眼面积大小对比如表3所示。 表3 不同吹氩流量下数值模拟和水模型实验渣眼面积对比 (a)数值模拟 (b)水模型实验 由图4可知,在底吹氩形成气泡羽流的冲击作用下,熔池液面渣层被上升流股冲开,渣眼边缘的底部渣层增厚,并在涌动钢液的带动作用下向四周扩展,钢液裸露,形成圆形渣眼。结合表3可知,随着吹氩流量的增大,渣眼面积逐渐增加。对比不同吹氩流量下的渣眼面积大小可知,数值模拟结果与水模型实验结果基本一致,误差处在3.90%~9.26%之间,所建模型的可靠性和准确性得到验证。 图5为总吹氩流量为240 L/min,不同吹氩模式下钢包内典型的气泡分布、速度分布、钢渣界面波动和湍动能分布,截面位置为与X轴平行的过透气砖中心的XZ截面。 图5 不同吹氩模式下钢包内典型流场 由图5可知,底吹氩钢包内,气泡从透气砖表面逸出进入熔池后逐渐向四周扩散,形成倒锥状的气泡羽流区,带动周围钢液上浮。受气泡羽流区外侧低速钢液阻滞作用的影响,上升流速度从气泡羽流区中心向两侧逐渐降低,并在冲击液面渣层后推动渣层向四周扩展,形成鼓包区或渣眼,并在此处造成较大湍动能;随后上升流转变为水平流,并在钢渣界面底部形成以气泡羽流为中心的涡流区。涡流区不仅能促使随气泡上浮至液面的夹杂物被液渣捕获去除,还能加强钢渣界面传质,加快精炼反应。 对比不同吹氩模式下钢包内流场可知,单孔吹氩虽然能在钢包内形成局部大环流,但由于湍流耗散使得环流的远端速度较低,对此处钢液的搅拌带动作用较弱;相比于双孔吹氩,由于单孔吹氩位置和数目限制,渣层易被吹开,卷渣概率较大。双孔等流量吹氩模式下,钢包内钢液流动更活跃,钢液上升流股速度小,对渣层的冲击力弱,钢渣界面相对稳定;然而,双孔吹氩所形成的气泡羽流在钢包上部相互碰撞,耗散底吹氩的驱动能,使得两上升流股之间存在流动不活跃区。双孔差流量吹氩时,吹氩流量的差异使得钢包内形成一强一弱两个上升流股,强流股可用于搅拌钢液,弱流股则有利于夹杂物的上浮去除,两者功能相互补充;同时,两流股的动量差异会造成强流股吸引弱流股的现象,有助于减小双流股之间的流动不活跃区。 不同吹氩模式下,吹氩流量对钢液速度分布的影响如图6和图7所示,吹氩流量对钢液湍动能分布的影响如图8和图9所示,其中截面位置为与X轴平行过透气砖中心的XZ截面,曲线位置为截面内Z=2.0 m 高度位置处。 图6 不同吹氩模式下钢包内速度分布 (a)G1 (b)G2 (c)G3 图8 不同吹氩模式下钢包内湍动能分布 (a)G1 (b)G2 (c)G3 由图6和图7可知,受气泡羽流空间分布的影响,透气砖上方钢液速度呈现中间高两边低的正态分布规律。随着吹氩流量的增大,气泡羽流中气泡数目增多,在浮力驱动作用下钢液速度逐渐增大。不同吹氩模式下钢包内钢液速度分布呈现出较大差异性。吹氩流量相同时,单孔吹氩模式下钢液上浮速度最大,双孔差流量吹氩中强流股上浮速度其次,双孔等流量吹氩中上升流股钢液速度最低。吹氩流量为240 L/min时,单孔吹氩、双孔等流量吹氩和双孔差流量吹氩中钢液上升流股最大速度分别达到2.25、1.49、1.70 m/s,表明钢液上浮的动能与气泡浮力密切相关,大吹氩流量下形成更多气泡上浮做功,充分搅拌钢液。 由图8和图9可知,钢液湍动能分布与钢液速度分布存在较大的相关性,两者变化规律基本一致。从分布对称性上看,单孔吹氩模式下,低吹氩流量时流股两侧湍动能分布较为对称;随着吹氩流量的增大,流股中心右侧湍动能明显较大,这与气泡羽流的附壁效应有关。当钢液上升流股速度加快时,流股与壁面间的压力减小,使得气泡羽流向壁面靠近;大吹氩流量下气泡羽流中气泡数目增多,气泡扩散过程中受到的壁面阻滞作用增大;受壁面摩擦作用的影响,上升流股在靠近壁面一侧形成较大的湍动能。该气泡附壁效应不仅消耗底吹氩的搅拌驱动能,还会导致底吹气泡带动钢液冲刷壁面内衬,造成钢包局部应力集中,降低钢包的使用寿命和安全性。 底吹氩钢包中钢渣界面行为的合理性十分重要,弱搅拌下需确保钢渣界面稳定,抑制顶渣卷混、二次氧化,强搅拌下则要避免熔池液面渣层被大面积吹开。不同吹氩模式下,吹氩流量对钢渣界面速度分布和渣眼面积的影响分别如图10和图11所示。 图10 不同吹氩模式下钢渣界面速度分布 图11 不同吹氩模式下渣眼面积 由图10可知,3种吹氩模式下钢渣界面速度随吹氩流量的变化趋势基本一致,均随吹氩流量增大而逐渐加快;当吹氩流量相同时,单孔吹氩模式下钢渣界面速度和流动不活跃范围最大,可能导致渣眼远端低流速区渣层冷凝结壳,影响精炼效果;双孔等流量吹氩下规律则相反,钢渣界面最大速度位于渣眼边缘鼓包的底部区,说明此处易受钢液剪切,发生卷渣。 钢包底吹氩对钢渣界面传质的促进作用主要体现在两个方面:①底吹氩钢包内熔池循环流动加快,钢渣界面流动速度增大;②钢渣界面的活跃流动范围增大。对于单孔吹氩模式,低吹氩流量下钢渣界面速度较小,活跃流动范围较大,这对钢渣界面传质具有一定的促进作用;随着吹氩流量增大,熔池内循环流动加快,钢渣界面最大速度增加,而活跃流动范围减小。双孔等流量吹氩模式下,钢渣界面最大速度和活跃流动范围均随吹氩流量的增大而增加,此时大吹氩流量更有利于钢渣界面反应。而双孔差流量吹氩模式下,强流股能快速搅拌钢液,弱流股使得钢渣界面即便在大吹氩流量时也能保持一定范围的活跃流动。 由图11可知,吹氩流量在120~240 L/min范围,相同吹氩流量下,单孔吹氩所形成的渣眼面积最大。这是因为低吹氩流量下渣眼面积主要受上升流股冲击力的影响,吹氩流量越大,气泡羽流到达钢渣界面后推动渣层的作用力越强。当吹氩流量超过240 L/min,双孔等流量吹氩模式形成的渣眼面积最大,双孔差流量吹氩所形成的渣眼面积最小。这与透气砖位置、数目和吹氩流量大小有关。大吹氩流量下,单孔吹氩所形成的气泡羽流由于受壁面限制,对渣层的驱动力在壁面处大量耗散,使得渣眼面积增长速率减缓;而双孔吹氩模式下上升流股分布宽度较窄,受壁面影响相对较小。 不同吹氩模式下钢包壁面剪应力分布如图12所示。可以看出,同一吹氩模式下,钢包壁面剪应力随吹氩流量的增大而增大,壁面最大剪应力分布在与透气砖同侧壁面上部和渣层下方。双孔等流量吹氩模式下,壁面剪应力分布范围明显增大,壁面存在3处应力集中区;双孔差流量吹氩下壁面剪应力集中区减少,表明壁面剪应力分布与钢包内气泡羽流行为密切相关。一方面,由于透气砖布置在钢包底部偏心位置,底吹氩所形成的气泡羽流在上升过程中会逐渐向临近的同侧壁面方向扩散,带动周围钢液冲刷壁面;另一方面,底吹氩在钢包内形成的环流也会不断冲刷壁面,与渣眼距离越近,意味着环流对壁面的冲击作用力越强。 图12 不同吹氩模式下壁面剪应力分布 壁面最大剪应力决定了钢包内衬耐材的流动侵蚀速率,而剪应力位置和面积分布规律对钢包内衬耐材的安装和替换有重要参考意义。图13为不同吹氩模式下钢包壁面最大剪应力、壁面最大剪应力距钢渣界面距离以及壁面剪应力大于1 Pa的区域面积。 (a)钢包壁面最大剪应力 (b)壁面最大剪应力距钢渣界面距离 (c)壁面剪应力大于1 Pa的区域面积 由图13可知,整体上来看,不同吹氩模式下钢包壁面最大剪应力均随者吹氩流量的增加而增大;单孔吹氩模式下壁面剪应力最大,双孔等流量吹氩模式下剪应力最小,并且两种双孔吹氩模式下壁面最大剪应力大小相近,仅相差1 Pa左右。吹氩流量为120 L/min时,单孔吹氩形成的壁面最大剪应力位于距钢渣界面0.32 m深度处,随着吹氩流量增大,最大剪应力距钢渣界面距离增加,其中单孔吹氩下最大剪应力距钢渣界面距离增幅最大,双孔差流量吹氩下该距离变化幅度最小。当吹氩流量为400 L/min时,由于单孔吹氩形成的渣眼靠近壁面并形成大量卷渣,导致此处的钢液环流发现显著变化,使得最大剪应力距钢渣界面距离大幅降低。从壁面剪应力面积来看,不同吹氩流量下,单孔吹氩下壁面剪应力面积较小,双孔等流量吹氩下壁面剪应力区域面积较大;当吹氩流量大于240 L/min时,双孔差流量吹氩下壁面剪应力面积随吹氩流量的增加而减小。由此可见,在缩短混匀时间、提高精炼效果的前提下[14],双孔差流量吹氩模式对钢包内衬耐火材料的流动侵蚀作用更小。 1)单孔吹氩模式下,钢包内局部大环流远端流速低,距透气砖远端的钢渣界面流动不活跃,易导致此处渣层冷凝结壳。双孔等流量吹氩模式下,当吹氩流量较低时,钢渣界面流动活跃,随着吹氩流量增加,虽然钢渣界面流速增大,但其流动活跃性降低。双孔差流量吹氩模式下,由于弱流股的搅拌作用,使得钢渣界面即便在大吹氩流量时也能维持一定范围的活跃流动。 2)吹氩流量在120~240 L/min范围,当吹氩流量相同时,单孔吹氩所形成的渣眼面积要大于两种双孔吹氩模式。而当吹氩流量超过240 L/min,双孔等流量吹氩形成的渣眼面积最大,双孔差流量吹氩所形成的渣眼面积最小。 3)对于3种吹氩模式而言,最大壁面剪应力位于与透气砖同侧壁面上部和渣层下部。单孔吹氩模式下,壁面剪应力最大,而壁面剪应力面积较小,双孔等流量吹氩模式下的规律与之相反;两种双孔氩模式下壁面最大剪应力大小相近,相差仅在1 Pa左右。综合考虑各方面因素,双孔差流量吹氩模式可以在提高钢液精炼效率的同时,降低钢包内衬耐火材料的流动侵蚀。1.4 边界条件及参数设置


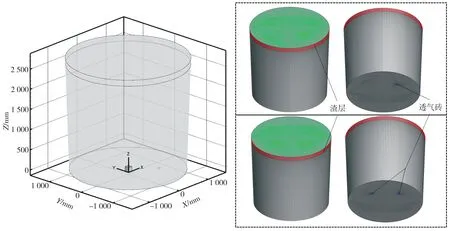
1.5 模型验证

2 结果与讨论
2.1 钢包内流场典型分布

2.2 钢包内速度和湍动能分布



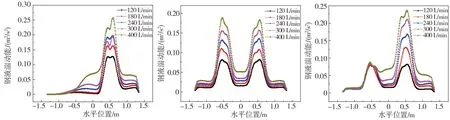
2.3 钢渣界面速度分布和渣眼面积

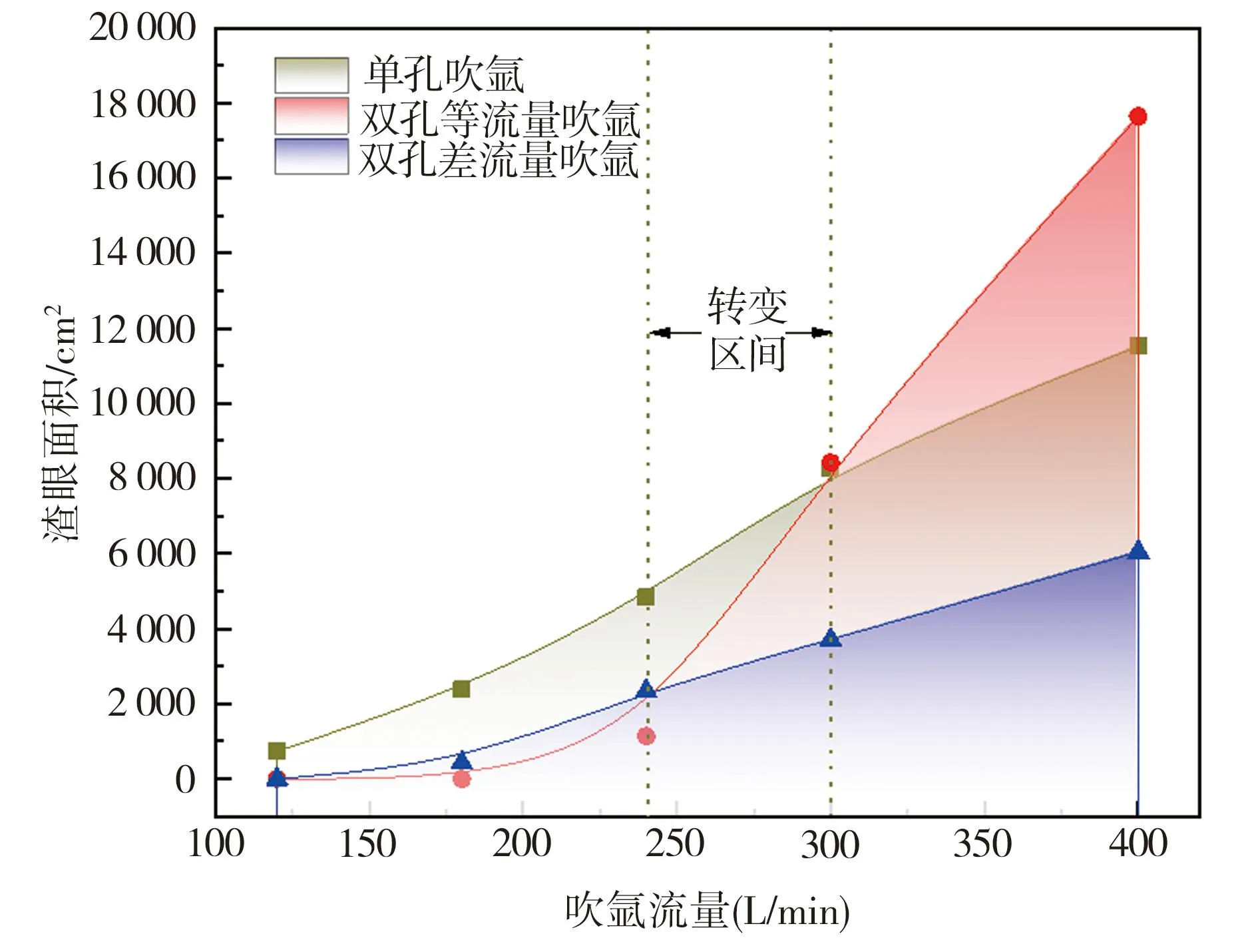
2.4 钢包壁面剪应力分布
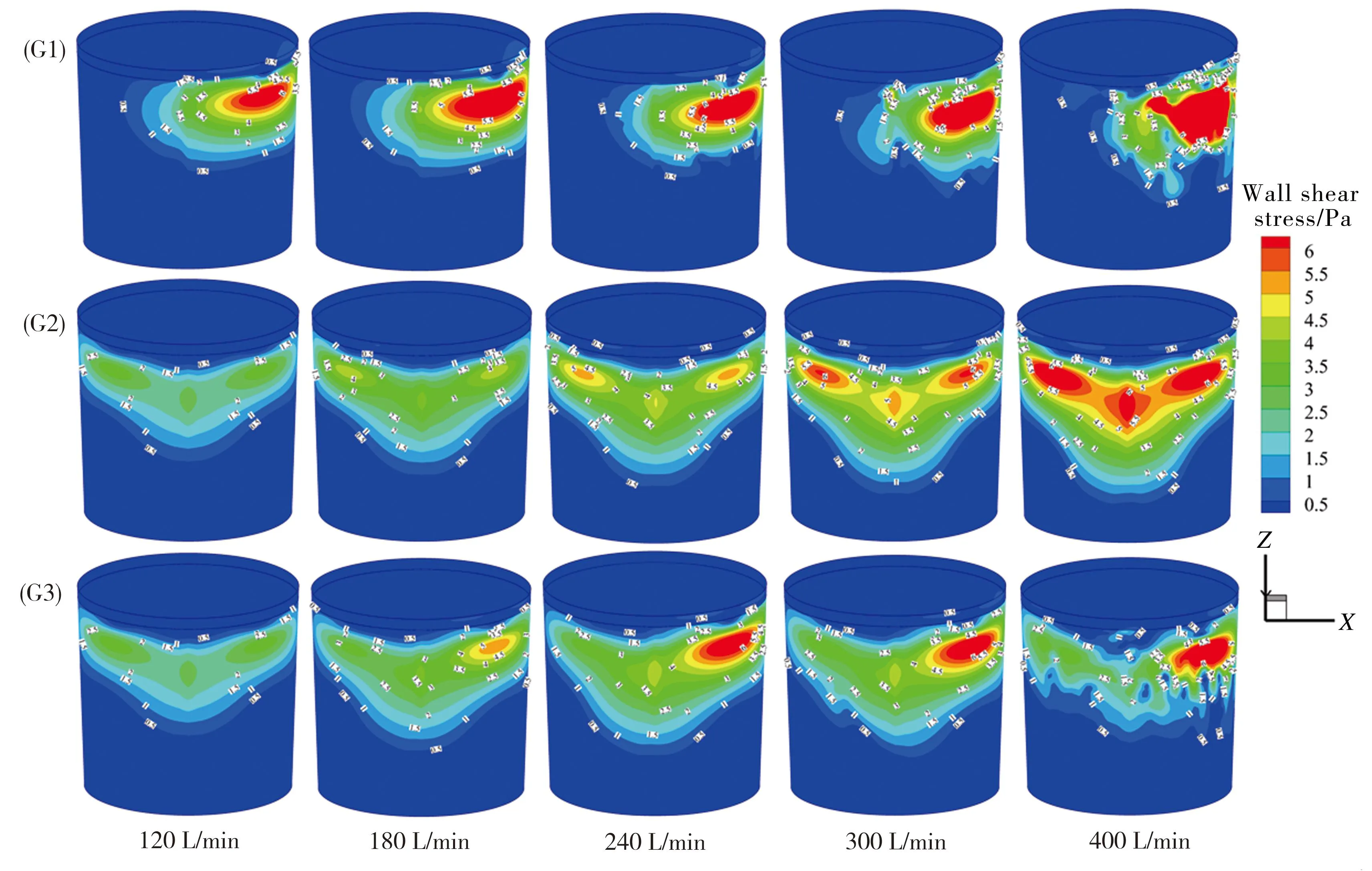
3 结论
