樽海鞘群算法基于动力学模型的改进

雷 灏, 赵品彰, 汪东华, 陈柏屹

(1. 江苏省计量科学研究院, 江苏 南京 210049; 2. 南京航空航天大学航天学院, 江苏 南京 210016)

0 引 言

随着社会发展和科技进步,各类工程问题的复杂度越来越高。在面对问题规模不断扩大的实际工程优化问题时,传统的基于梯度的数值优化算法难以有效求解。受自然中群体行为启发而提出的群智能优化算法[1-6]不依赖具体问题特征和梯度信息,具有简单高效的结构,受到越来越多学者的关注和研究[7]。常见的群智能优化算法包括灰狼优化(grey wolf optimizer, GWO)算法[8-11]、人工蜂群(artificial bee colony, ABC)算法[12-14]、鲸鱼优化算法(whale optimization algorithm, WOA)[15-22]等。为了进一步挖掘群智能算法的性能,不断有学者提出新的智能优化算法来求解复杂的全局优化问题[23]。

樽海鞘群算法(salp swarm algorithm, SSA)是Mirjalili等[24]在2017年新提出的基于种群的智能优化算法,该算法模拟了樽海鞘群以偏序运动链式的方法进行捕食的过程,具有参数少、结构简单的优点。然而也存在迭代后期种群多样性减少、易于陷入局部最优的不足,从而限制了算法的开发和探索能力。为了进一步提高SSA的性能,国内外学者对原始SSA做出了相应的改进。

在算法参数选择上,Qais等[25]在基准SSA的基础上,采用游走补偿随机化与跟随率随机化提出了一种加强SSA。改进后的算法具有更快的收敛速度,与SSA相比能够更有效地求解多目标函数。为了增强追随者位置更新的灵活性,王宗山等人[26]引入了一种非线性递减惯性权重来评价前一个个体对当前追随者的影响程度。黄小根等人提出一种多策略驱动的改进SSA[27]。在领导者位置更新公式中引入指数衰减因子,改善算法的全局收敛速度;在跟随者位置更新公式中引入随机惯性权重算子,以协调并增强算法的局部开采和全局勘探能力。陈忠云等人选择Schaffer测试函数,通过仿真分析确定漫游步长中的指数设置为2.5为最优[28]。

在算法结构上,陈忠云等人引入正弦余弦算法在算法执行后期代替SSA的链式机制[29]。王宗山等人提出一种基于正交设计的折射反向学习算法[26],有效增强了算法的全局勘探能力,同时减少函数的评价次数,改善了算法的整体性能。为了解决部分遮蔽条件下光伏系统最大功率跟踪问题,杨博等人[30]提出一种具有多链结构的改进SSA。采用多个樽海鞘链同时进行独立寻优,以提高算法全局搜索和局部搜索的能力;同时,通过群落中所有樽海鞘间的信息交流,重组产生新的樽海鞘链,以提高算法的收敛稳定性。3个算例结果表明所提算法能在部分遮蔽条件下快速、稳定地获取最大光能。

与基于梯度近似的群智能算法不同(比如粒子群优化(particle swarm optimization, PSO)算法、GWO、WOA等),SSA采用偏序主从运动链的形式,通过领导者在当前全局最优解处的随机游走实现对设计空间的探索,以偏序学习的机制形成运动链的惯性,进而提高领导者随机游走的遍历性,随着迭代过程的推进,领导者随机游走的强度逐渐衰减,完成算法收敛。根据以上讨论,SSA的改进大致可以归为三类:领导者选择机制的改进[31]、随机游走机制的改进[25,32]以及偏序跟随率的改进[25-26,28-29]。现有文献通过改进学习机制有效改善了算法的性能,但是对于算法性能提升的原因缺乏原理性的解释,无法在改进算法的同时保证算法的稳定性和收敛性。

从收敛性分析的角度出发,本文首先建立了SSA的动力学模型,并且从控制系统稳定性的角度推导了算法稳定的条件以及SSA收敛到全局最优点的条件。基于建立的动力学模型,对改进策略进行了总结,通过引入异质定常跟随率和多链结构,本文还提出了新的多链异质SSA,仿真结果表明改进算法的探索性和多样性有所改善。通过求解CEC2017测试函数,并与其他算法进行对比,验证了本文提出的改进策略的有效性和改进算法的优越性。

1 SSA动力学建模

受启发于海洋中樽海鞘的群体游动特性,Mirjalili等[24]提出了SSA。该算法采用偏序运动链的形式更新个体在设计空间中的位置,其中位于偏序位置首位的个体称为领导者,其他的个体均称为跟随者,该算法通过领导者的随机游走实现对设计空间的探索,利用偏序跟随者的延时运动发现更优位置,在算法执行后期,通过收缩领导者随机游走的范围,确保算法在全局最优解处收敛。

1.1 SSA的基本形式

在基准SSA中,定义第1个个体为领导者,其位置更新算法满足:

(1)

(2)

式中:T表示算法迭代最大次数;r2表示服从(0,1)均匀分布的随机变量。

领导者的位置更新机理可以理解为在全局最优点处的随机游走,游走尺度由控制参数c确定。算法中跟随者的更新机理表示为自身位置与前序位置的平均位置:

(3)

式中:i= 1,2,…,N,N表示种群规模。基准SSA由式(1)和式(3)组成,分别对领导者与跟随者的位置进行更新。

考虑到设计空间中各维数之间无相互影响,则可以将一个D维的离散系统转化为D个1维的离散系统,且各系统之间的稳定性具有一致性。因此,本文后续仅针对1维的离散系统进行讨论。

1.2 SSA的动力学模型

樽海鞘群基准算法的动力学模型可以通过构建群状态的差分方程实现,将式(1)中等号的右半部分可以表示为随机变量cr,j的形式:

(4)

定义离散系统的状态量为种群中所有个体第j维的取值:

Xj(k)=[x1,j(k),x2,j(k),…,xN,j(k)]T

则式(4)可以转化为N阶离散系统动力学的差分方程形式:

(5)

式(5)可以表示为矩阵形式:

Xj(k+1)=AXj(k)+Bbg,j(k)+Dcr,j(k)

(6)

式中:状态量Xj(k)的第一维表示领导者j维位置,其余维表示跟随者j维的位置;矩阵A为N维方阵,矩阵A、B、C决定了种群j维位置的更新方式。

由于基准SSA的算法模型可以转化为离散系统的差分方程组(6)的形式,则可以通过分析离散动力学模型(5)获得SSA的稳定性和收敛性,如果系统的状态空间模型(6)稳定收敛,则多次迭代后状态量收敛到唯一解,即种群j维的位置收敛到唯一值。式(6)中,系统的控制输入可以视为全局最优位置bg,j,而算法中的领导者随机游走行为等价为动力学系统的随机扰动。

与基于近似梯度的PSO算法、GWO算法等不同,SSA一般具有偏序运动链的特征。考虑到SSA的变种,可以进一步将SSA泛化表示为具有参量的形式为

Xj(k+1)=A(a,b)Xj(k)+B(c)bg,j(k)+D(d)

(7)

式中:

式中:a= {ai},b= {bi},i=2,3,…,n。将式(7)转化为常规形式:

(8)

式中:c表示领导者对全局最优解的学习因子;d表示领导者在全局最优解处的随机游走;bi表示跟随者i自身的惯性因子;ai表示跟随者i对于前序对象的学习因子,在基准算法中,各参数具有如下定义:ai=bi=1/2,c=1,d(k)=cr,j(k)。

2 SSA稳定性分析

2.1 稳定性分析

差分系统的稳定性由状态矩阵的极点分布确定,当系统的极点分布在z平面的单位圆之内系统稳定。根据离散系统的稳定性理论可知,系统具有全局渐进稳定性。

定理 1SSA收敛性定理。考虑具有与式(8)相同算法结构的SSA。当|bi|<1,i=2,3,…,n时,算法收敛。

证明算法结构式(8)与离散系统(7)等价,即算法(8)的收敛性与离散系统(7)的稳定性一致。离散系统(7)的稳定性由系统状态矩阵A(a,b)确定。根据矩阵论计算得到状态矩阵A(a,b)的极点为

zi={0,b2,b3,…,bn}

当|bi|<1,i=2,3,…,n时,根据离散系统稳定性原理,系统具有N-1个位于z平面单位圆内且在实轴上的极点,因此离散系统(6)稳定,即算法收敛。

证毕

2.2 终值平衡点分析

考虑迭代次数很大的情况下,以全局最优点作为驱动量,当系统满足稳定性条件时,系统收敛到一个平衡点。该平衡点与全局最优点之间的关系由如下定理确定。

定理 2SSA终值定理。当算法收敛的前提下,当k→∞,全局最优量bg,j恒定,且扰动d(k)→0时,算法最终状态收敛于平衡点:

(9)

证明考虑系统差分动力学模型(7),若系统扰动为0时,则系统收敛,且满足:

Xj(k+1)=Xj(k)=Xj(∞)

(10)

将式(10)代入式(7)可以推导得到:

Xj(∞)=(I-A)-1Bbg,j

(11)

将式(11)推导展开即可得到式(9)。

证毕

推论 1SSA全局最优收敛条件。考虑到具有偏序运动链的算法结构(8),需要满足如下4个条件才能确保系统收敛到最优点:

(ⅰ) ∀k>Tc,|bi(k)|<1,i=2,3,…,n

由于系统收敛,根据定理1可以得到条件(ⅰ),表示存在迭代次数Tc,当迭代次数k大于Tc时,动力学系统的惯性因子bi的模值要小于1;要求系统收敛到全局最优点,根据定理2以得到条件(ⅱ)～条件(ⅳ)。

3 基于动力学模型的算法改进

根据SSA的动力学模型可以从以下几个方面对算法进行改进:根据系统状态矩阵A的定义可以建立链运动的跟随律;根据系统的控制矩阵B的定义可以建立链首对驱动量的学习机制;根据系统的驱动量u的定义可以建立系统的驱动机制;根据系统扰动量d的定义可以建立系统的游走机制。关于SSA动力学差分方程中各参数与因式的物理解释可参考图1。

图1 跟随律基于动力学分析的代数解释Fig.1 Algebraic interpretation of the following law based on dynamic interpreter

通过动力学分析可知,学习律在一定程度上影响了算法的收敛性和搜索性,但是影响程度有限。从代数解析的角度分析,学习律过程的变化对于算法本身的收敛性没有影响,只需要保证当迭代次数增加时,学习率趋近于1即可。从几何的角度分析,学习律的变化影响的是领导者学习中心的变化,其决定了领导者当前迭代周期的游走中心,在一定程度上提高了系统搜索性。

此外,游走机制也可以通过增加系统的随机性来提高算法的搜索性,比如通过莱维飞行模式[33]、高斯变异[34]、混沌模型[35]等方式进行游走。本文具体讨论跟随律和驱动机制的改进思路。

3.1 跟随律改进

算法模型的跟随律指的是个体自身的惯性因子bi与偏序学习因子ai随迭代次数的变化规律。根据定理1可知,系统的收敛性仅与惯性因子bi有关。因此,根据收敛速率与系统极点的关系,可以直接确定系统收敛速率。

系统状态收敛速率的差异在一定程度上表征了算法对过程状态的遍历能力。在基准SSA中,惯性因子为常数0.5,种群中所有个体具有相同的收敛速率。因此,从提高算法遍历能力的角度出发,可以设计不同收敛速率的跟随率。

根据SSA机理可知,领导者承担了领域探索的角色,其前后迭代步长变化的随机性最大。跟随者的探索步长的大小可以视为对领导者探索区域的二次探索。若跟随者惯性因子越小,则迭代步长越大,收敛性越强。因此,可以根据跟随偏序集为每一个个体指定不同的惯性因子:前序个体惯性因子较小,以较快速度收敛于跟随者,确保对未知区域的快速探索;后序个体惯性因子较大,收敛性较慢,使得整个樽海鞘群的运动链具有“拖尾”效应,确保群体在领导者的探索包络内具有更细致的探索能力。

(12)

式中:bmin,bmax表示惯性因子变化范围,其中bmax<1,bmin>0。

此外,为了确保算法具有全局最优的收敛条件,根据推论1中的条件(ⅱ)可知,在满足式(12)的基础上,需要对偏序学习因子ai进行约束,才能确保算法满足全局最优的收敛性,ai表达式为

ai=1-bi,i=2,3,…,n

(13)

图2中给出了几何解释,其中空心圆表示当前个体位置,实心圆表示算法迭代后的更新位置,黄色五角星表示当前的全局最优解,黄色的圆圈表示当前迭代中算法所获得的全局最优位置。越接近于领导者的个体对前序位置跟踪的越快,从而强化了领导者游走的探索效果。

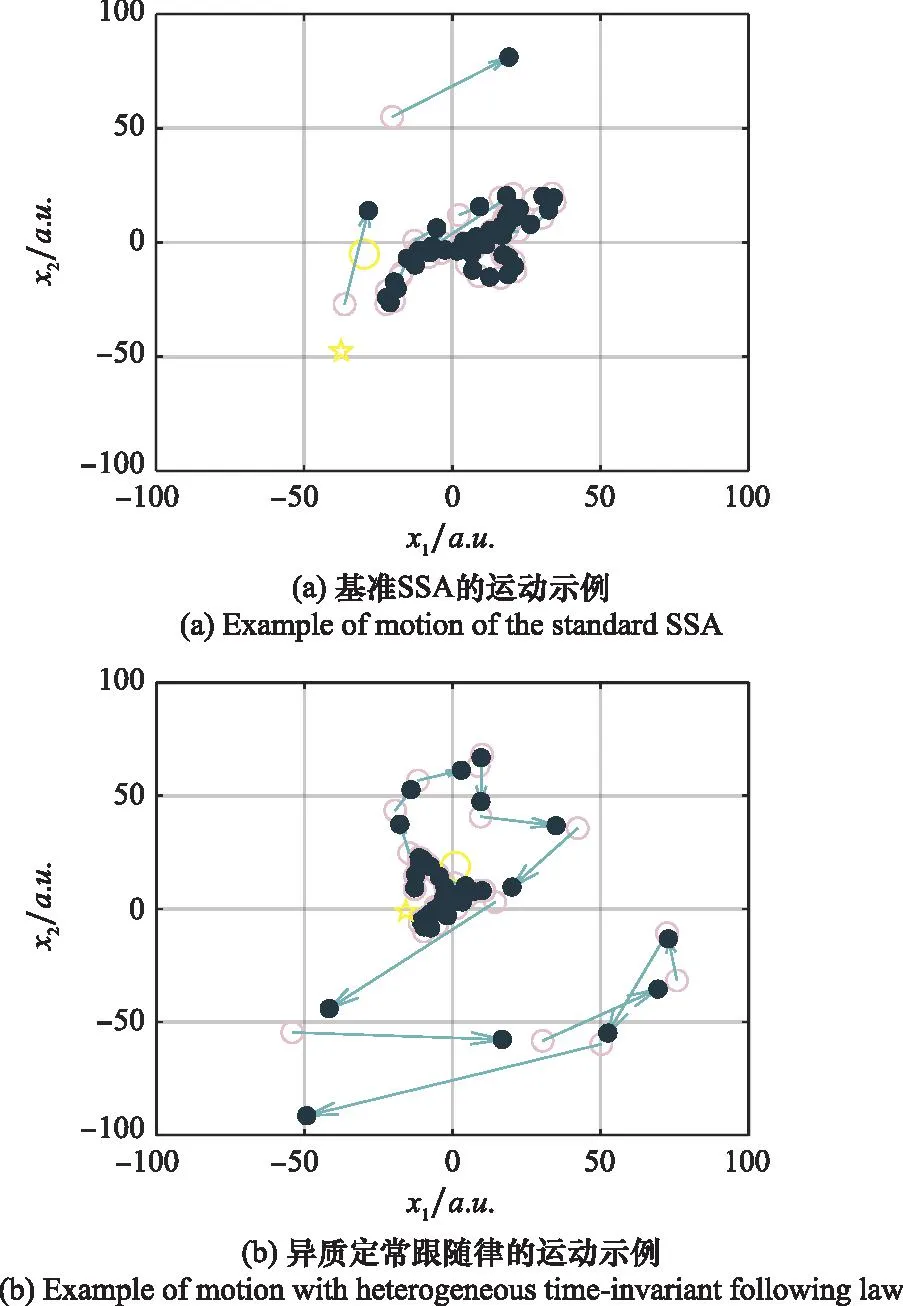
图2 跟随律基于动力学分析的几何解释Fig.2 Geometric interpretation of heterogeneous following law

3.2 驱动机制改进

SSA一般采用单链形式,即驱动量为迭代过程中所获得的全局最优解。根据动力学形式可知在搜索过程中可以通过调整驱动量,即学习对象来提高算法的搜索性。一般算法中学习对象可以是全局最优解、全局次优解、个体历史最优解、随机对象等。

因此,可以通过构建多运动链结构,同时指定多个学习对象提高算法的多样性。从算法结构上将种群个体分为确定的若干个子链,每一个子链确定偏序运动。

首先,将种群中的个体进行编号,种群规模为N,定义运动链的总数为Mc,则各个运动链中个体的数目为

第m个运动链中领导者及后续跟随者对应的编号为

式中:i=1表示领导者;i=2,3,…,Nm表示跟随者。

在将种群划分多链的基础上,驱动机制改进的核心在于对于每一个子链指定不同的学习对象。可以采用随机化个体或者偏序最优解。本文中采用的改进机制为偏序最优解,即每一个子链的领导者的学习中心分别指定为排序后的最优解位置。

以具有3个运动链的算法结构为例,则3个领导者的更新机理为

(14)

式中:上标1、2、3表示子链序号;br1=bg;br2表示仅次于bg的位置;br3次之。

3.3 基于动力学行为的算法改进

在基准SSA的基础上,采用以上两种改进策略,提出了多链异质SSA(multi-chain heterogeneous SSA, MHSSA)。

首先,设置运动链的个数,将种群中的个体按照运动链的从属关系进行分类,并在同一个运动链中以固定排序的形式建立偏序运动链。各运动链中,异质惯性因子根据偏序集定义为

b=linspace(bmin,bmax,Nl-1)

(15)

式中:bmin=0.1,bmax=0.9,运动链排序越靠前的个体惯性因子越小;Nl表示第l个子链的个体总数。

以上改进措施均在算法初始化的时候完成,后续算法执行过程中与基准SSA的流程相似,且计算量相当,未增加算法对算力的负荷。算法的执行流程如下。

步骤 1初始化:定义种群规模N,运动链个数Mc,偏序结构,根据式(15)定义各个个体的跟随率;

步骤 2适应度计算:根据种群位置计算适应度;

步骤 3更新最优序列:根据当前适应度对个体进行排序,并更新最优序列;

步骤 4迭代终止条件判断:判断是否满足终止条件。如果满足,则输出当前最优序列中的首项作为全局最优解;否则执行步骤5;

步骤 5多链领导者选择:选择当前最优序列中前Mc个个体位置分别作为不同运动链的驱动量;

步骤 6位置更新:根据式(7),更新种群位置信息,并跳转至步骤1。

算法流程图如图3所示,其中本文所提出的改进流程以粗体凸显。

图3 MHSSA的流程图Fig.3 Flowchart of MHSSA

4 仿真与验证

4.1 测试函数及仿真设置

本文的仿真对象选择CEC14中定义的16个简单函数(3个单谷函数、13个多谷函数),6个混合函数与8个组合函数共30个函数组成仿真测试集。单谷函数用于检验算法的收敛精度,多谷函数用于测试算法跳出局部最优的能力,混合函数和组合函数组成复杂,可用于测试算法解决现实世界复杂优化问题。其中,设计空间的搜索范围定义为[-100,100]D,其中D表示设计变量x的维数。

在每次的仿真测试过程中,需要对全局最优解进行随机化处理:全局最优随机偏移与设计空间的随机扭转。令o表示偏移后的全局最优解,在[-80,80]D范围内随机指定。令M表示为旋转矩阵,对所有的函数与基函数均进行设计空间的旋转。

本文中优化问题考虑的维数为D=30,种群规模设置为

单个问题仿真的次数为51次,考虑到算力的约束限制,本文中约定最大迭代次数为

仿真研究的算法主体为采用异质跟随及多链驱动改进的MHSSA,仿真对比以基准SSA、仅采用异质跟随率改进的异质SSA(heterogeneous, HSSA)、仅采用多链驱动改进的多链SSA(multi-chain SSA, MSSA)进行纵向对比;同时采用公开文献中其他的SSA改进算法进行横向对比,包括多子群的共生非均匀高斯变异SSA(multi-subpopulation based symbiosis and non-uniform Gaussian mutation SSA, MSNSSA)和基于正交设计的折射反向学习SSA(orthogonal opposition-based SSA, OOSSA)。为了说明SSA的适用范围,对比了PSO算法和GWO算法。

4.2 仿真结果

表1列出了30个测试函数下不同算法的统计学特征平均排名,Med、Var、Min、Max分别表示51次运行结果的中位数、标准差、最小值和最大值,包括本文提出的MHSSA在内的所有算法都能够收敛。

表1 算法统计学特征平均排名比较Table 1 Comparison of average rank for statistical characteristics of algorithms

从表1中可以看出本文提出的MHSSA在中位数、标准差、最小值、最大值上均名列第1,表明改进后的算法在寻优能力上有更好的表现,由于各算法在标准差上的差异不显著,不考虑标准差排名,MSSA在中位数、最大值、最小值上均排名第2,其余算法在中位数、标准差、最大值、最小值上的表现各有千秋。

为了避免算法对比中随机性所造成的性能差异,本文用p值检验来进行显著性验证,对比MHSSA与其他各个算法的差异性。显著性水平设置为0.05。验证结果如表2所示,其中,S表示MHSSA算法具有显著性差异,NS表示没有显著性差异;“+”表示MHSSA算法优于对比算法,“-”表示MHSSA次于对比算法。

表2 算法性能差异显著性比较Table 2 Significance testing of algorithms

从表2可以看出MHSSA在28个测试函数上显著优于SSA,在28个测试函数上显著优于HSSA,在12个测试函数上显著优于MSSA,在29个测试函数上显著优于MSNSSA,在20个测试函数上显著优于OOSSA,在24个测试函数上显著优于PSO,在19个测试函数上显著优于GWO。

为了更直观地表示算法性能差异显著性比较结果,图4对比较结果进行了统计,其中绿色部分表示MHSSA显著优于对比算法,白色部分表示对比结果不显著,无法排除结果是由于偶然性导致,蓝色部分表示MHSSA显著次于所对比的算法。

图4 MHSSA与其他算法的显著性对比Fig.4 Significance comparison between MHSSA and other algorithms

从图4中可以直观地看出,MHSSA与SSA和MSNSSA相比,在所有测试集函数中均有明显改善。整体而言,异质跟随率与多链驱动机制的结合要更优于采用单一改进机制的算法。此外,MHSSA在6个测试函数的结果中显著次于OOSSA。进一步分析可以发现,这些函数均具有周期性振荡小幅衰减的函数。可以认为针对这类型函数OOSSA有明显的优势,虽然本文改进的算法在以上6个函数上未收敛到最优解,但是距最优解的距离与其他算法相比更小。

根据图4中显著性分析结果,分别选择MSSA、OOSSA、PSO与GWO对比在不同测试函数优化结果中中位数的排名情况,如图5～图8所示。

图5 CEC14测试函数集MHSSA与MSSA的中位数排名对比Fig.5 Median rank of MSSA and MHSSA for CEC14 testsuite

从图5中可以看出,MHSSA由于新增了异质跟随律这一机制,在多谷类型的优化问题中显著提高优化性能;从图6中可以看出,多数情况下MHSSA的优化结果是优于OOSSA的,但是对于次优解分布密集且目标函数具有周期性振荡小幅衰减的情况下,OOSSA具有较好的表现;从图7和图8中可以看出,相较于PSO和GWO,本文提出的MHSSA在多数情况下也具有较好的性能表现,对于设计变量空间未经过旋转随机化的测试函数,比如F08和F10,PSO的优化结果更优。

图6 CEC14测试函数集MHSSA与OOSSA中位数排名对比Fig.6 Median rank of MSSA and OOSSA for CEC14 testsuite

图7 CEC14测试函数集MHSSA与PSO中位数排名对比Fig.7 Median rank of MSSA and PSO for CEC14 testsuite

图8 CEC14测试函数集MHSSA与GWO中位数排名对比Fig.8 Median rank of MSSA and GWO for CEC14 testsuite

为进一步说明不同算法在典型测试函数上的性能的优劣,根据各算法独立求解测试函数51次的结果绘制箱式图,选择了算法具有显著对比差异的部分函数,以多峰函数、混合函数和组合函数为分组依据,如图9～图12所示。

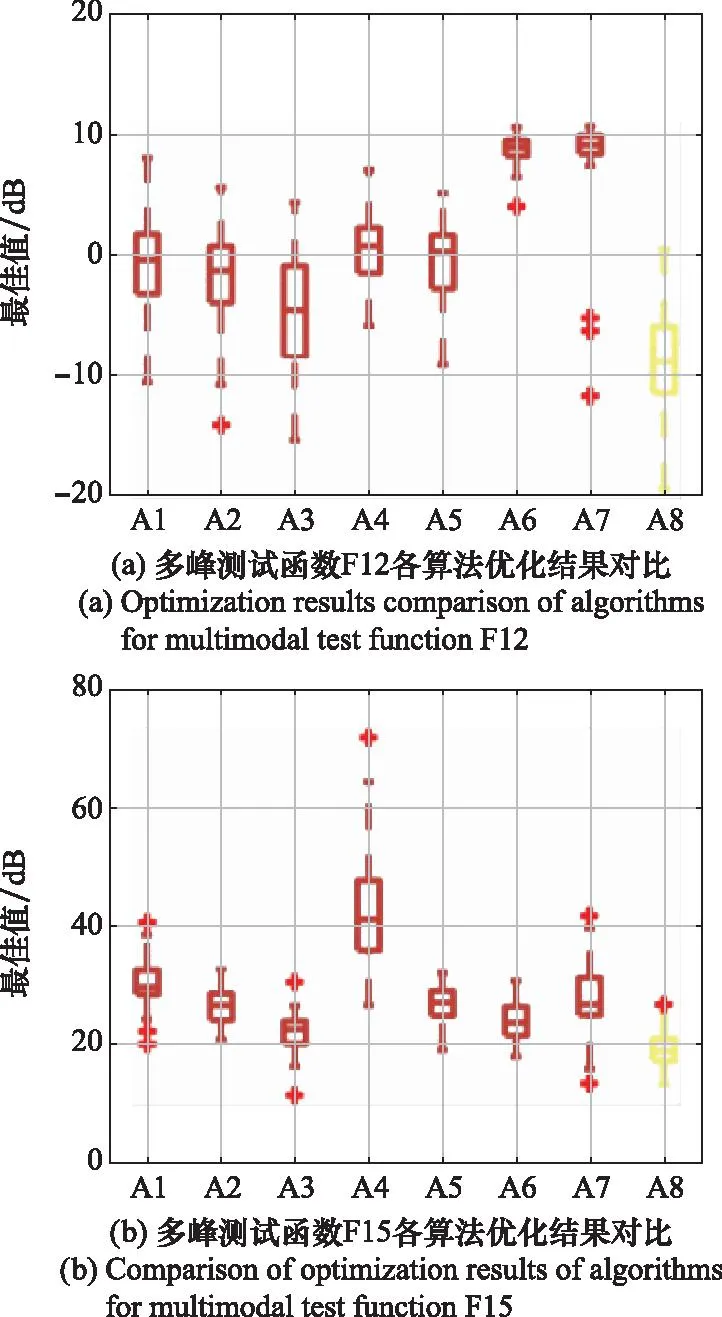
图9 多峰测试函数各算法优化结果对比Fig.9 Optimization results comparison of algorithms for multimodal test functions

图10 组合测试函数各算法优化结果对比Fig.10 Optimization results comparison of algorithms for combined test functions

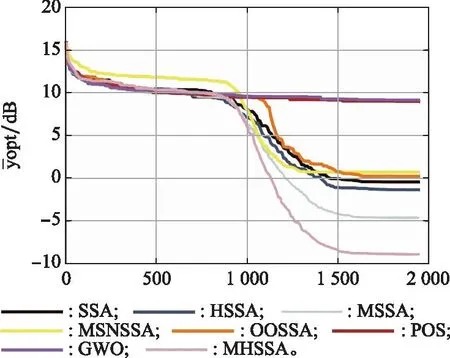
图11 多峰测试函数F12最优值中位数收敛曲线对比Fig.11 Median convergence trajectory comparison of optimal value for multimodal test functions F12

图12 组合测试函数F24最优值中位数收敛曲线对比Fig.12 Median convergence trajectory comparison of optimal value for combined test functions F24

其中A1表示SSA;A2表示HSSA;A3表示MSSA;A4表示MSNSSA;A5表示OOSSA;A6表示PSO;A7表示GWO;A8表示MHSSA。对比性能最优算法以黄色标识。

5 结 论

本文以SSA为研究对象,从动力学的角度出发,将算法更新机理解构为离散动力学方程,提出了算法稳定性的充分条件。根据SSA的动力学解释模型,归纳总结了该算法的四类改进措施:跟随律改进、学习律改进、驱动机制改进与游走机制改进。基于SSA收敛性条件,从跟随律与驱动机制两个方面提出了异质定常跟随律与多链驱动的算法改进措施。通过优化算法测试集的仿真结果,分别验证了两种改进的有效性,在不增加算法算力负荷的情况下,显著改善了SSA的算法性能。仿真对比表明,改进措施对测试集中绝大多数函数的优化结果均有显著改善;对于次优解分布密集且目标函数具有周期性振荡小幅衰减的情况,比如Rastrigin函数,采用正交策略可以获得更优的情况。