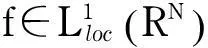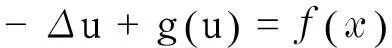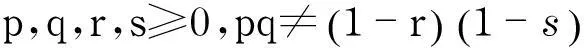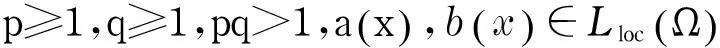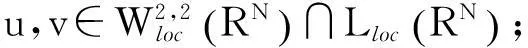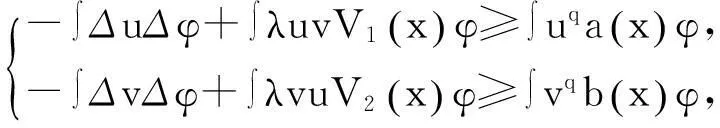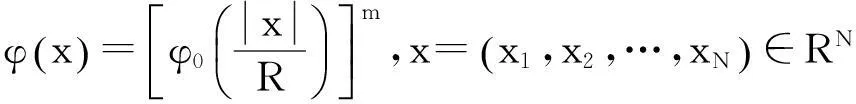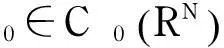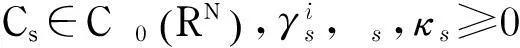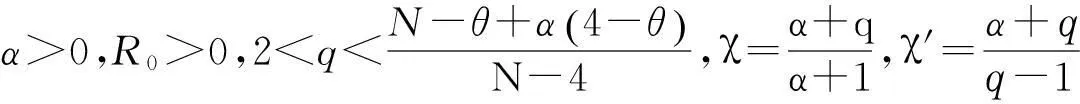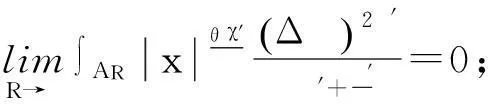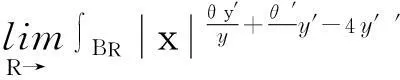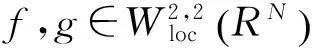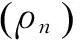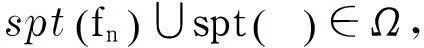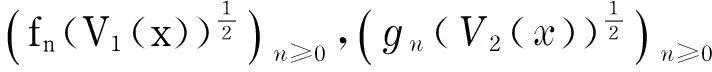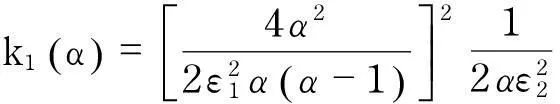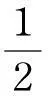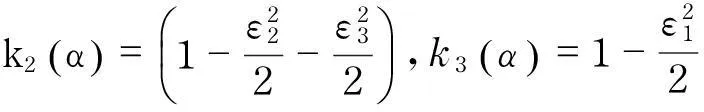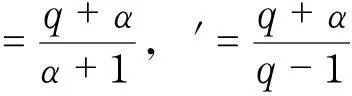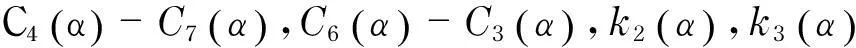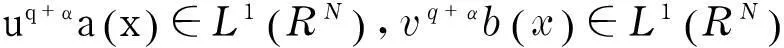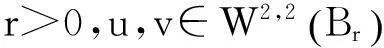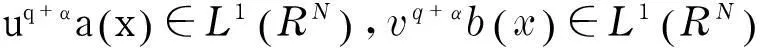带势函数的双调和不等式组的整体解的不存在性

蒋秋霞，　魏公明

(上海理工大学 理学院,上海　200093)



带势函数的双调和不等式组的整体解的不存在性

蒋秋霞，魏公明

(上海理工大学 理学院,上海200093)

摘要：研究了一类带势函数的双调和不等式组的整体解的不存在性.在一定条件下,通过选择合适的测试函数,利用Young不等式、Hölder不等式及Sobolev嵌入定理等,得到解的先验估计,并应用这一估计证明不等式组的整体解的不存在性.

关键词：双调和; 测试函数; 整体解

1问题的提出

研究不等式组

(1)

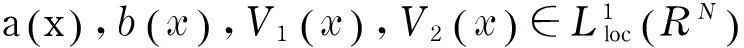
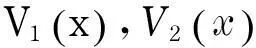
(3)

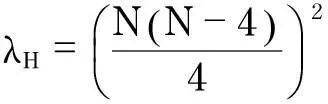
文献[1]给出了四阶Schrõdinger不等式

(4)

的先验估计.

Brezis[2]研究了下列问题：

令1

而且,如果在RN上，几乎处处有f≥0,则几乎处处有u≥0.

Quittner[3]研究了下列方程:

Yarur[4]研究了下列方程:

在Ω⊂RN上,

Mitidieri等[5]通过选取合适的测试函数，证明了拟线性椭圆方程正解的不存在性.

Gidas等[6-7]给出了刘维尔定理与各种半线性、拟线性椭圆方程的先验估计解之间的联系.有关拟线性算子的更一般的结论见文献[8-9].

受以上文献的启发,本文研究双调和不等式组(1),通过解的先验估计来证明不等式组的整体解的不存在性.给出一些辅助的引理,证明双调和不等式组的整体解的不存在性.

2预备知识和重要引理

定义1令N>4,称u,v是不等式组(1)的弱解,若它们满足下列条件:

(5)

(6)

而且,若d>0,有

(7)

其中,C与R无关.

证明参考文献[1],应用引理1中的式(7),对∀R>0,有

a.

(8)

b.

(9)

c. 运用球坐标换元,有

其中,常数C不依赖于R.

由于

所以

且

在式(8)～(10)中,指数为负,令R→,即a,b,c得证.

在Ω中,几乎处处有

(11)

由Hardy不等式(3),可知

(12)

应用柯西施瓦茨不等式

(13)

再次应用柯西施瓦茨不等式,有

(14)

(15)

因此,应用式(13)和式(14)，有

再应用Fatou引理,引理2得证.

将不等式组的右边第1项展开移项,有

(16)

(17)

(18)

(19)

将式(17)和式(18)代入式(16)，有

(20)

a.

b.

c.

将a,b,c代入式(20),有

其中

将式(21)与式(22)相加,有

因为,C与φ无关,所以,有

其中,常数C与r无关.

3主要结论

现证明定理1.

定理1令u,v是不等式组(1)的弱解,且满足定义1及在RN上,几乎处处有:u≥0,v≥0,Δu≥0,Δv≥0,则有,u=v≡0,即不等式组(1)不存在整体解.

证明取α>2,使得

易证uσ,vσ满足引理4的假设,∀r>0,有

因为,N>4>θ,所以,当r→时,有‖uσ‖L(Br)+‖vσ‖L(Br)≤0,则u=v≡0.

参考文献：

[1]Cárdenas G M.A priori estimates for nonlinear fourth order Schrödinger type equations[EB/OL].[2013-12-15].http:∥arXiv:1312.4168v1[math.AP].

[2]Brezis H.Semilinear equations inNwithout condition at infinity[J].Applied Mathematics and Optimization,1984,12(1):271-282.

[3]Quittner P.A priori estimates,existence and Liouville theorems for semilinear elliptic systems with power nonlinearities[J].Nonlinear Analysis,2014(102):144-158.

[4]Yarur C S.Nonexistence of positive singular solutions for a class of semilinear elliptic systems[J].Electronic Journal of Differential Equations,1996(8):1-22.

[5]Mitidieri E,Pokhozhaev S I.Non existence of positive solutions for quasilinear elliptic problems inN[J].Proceedings of the Steklov Institute of Mathematics,1999(227):192-222.

[6]Gidas B,Spruck J.Global and local behavior of positive solutions of nonlinear elliptic equations[J].Communications on Pure and Applied Mathematics,1981,34(4):525-598.

[7]Gidas B,Spruck J.A priori bounds for positive solutions of nonlinear elliptic equations[J].Communications in Partial Differential Equations,1981,8(6):883-901.

[8]D’Ambrosio L,Mitidieri E.A priori estimates,positivity results,and nonexistence theorems for quasilinear degenerate elliptic inequalities[J].Advances in Mathematics,2010,224(3):967-1020.

[9]Serrin J.Entire solutions of quasilinear elliptic equations[J].Journal of Mathematical Analysis and Applications,2009,352(1):3-14.

[10]Maly J,Ziemer P.Fine regularity of solutions of elliptic partial differential equations[M].Providence:American Mathematical Society,1997.

(编辑:石瑛)

Nonexistence of Global Solutions for a Class of Biharmonic Inequalities

JIANG Qiuxia,WEI Gongming

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：The nonexistence of golbal solutions for a class of biharmonic inequalities was studied.Under certain conditions,by choosing appropriate test functions and using the Young’s inequality,Hölder’s inequality,Sobolev type inequalities,a priori estimate for the solutions was obtained and the nonexistence of the golbal solutions for the systems was proven.

Keywords：biharmonic; test function; global solution

中图分类号：O 175.25

文献标志码：A

通信作者：魏公明(1974-),男,副教授.研究方向:偏微分方程.E-mail:gmweixy@163.com

基金项目：沪江基金资助项目(B14005)

收稿日期：2015-01-08

DOI：10.13255/j.cnki.jusst.2016.02.002

文章编号：1007-6735(2016)02-0109-06

第一作者： 蒋秋霞(1990-),女,硕士研究生.研究方向:偏微分方程.E-mail:qxjiangsx@126.com