非圆齿轮泵流量特性分析及脉动优化方法
2024-01-16张奕周凯红佘东
张奕,周凯红,佘东
(桂林理工大学机械与控制工程学院,广西桂林 541006)
0 前言
非圆齿轮泵是一种新型容积泵,兼具圆齿轮泵和凸轮泵的优势[1],具有大排量、高容积效率的特点,其排量比圆齿轮泵高出4倍,广泛应用于农林业[2]、石油化工[3]、汽车[4]、医疗[5]等领域。大排量的流体输送过程极易产生剧烈的瞬时流量脉动,导致输送不稳定,引起泵体与管道的振动和噪声[6],严重限制了非圆齿轮泵在工程实际中的应用。
刘大伟等[7-8]提出一种以非圆齿轮为驱动系统的椭圆齿轮泵,降低了流量脉动率。谭伟明[9]提出一种并联卵形齿轮泵平抑流量脉动,其平抑原理为流量补偿。曾庆敦等[10]实现了并联卵形齿轮泵的三维数值模拟仿真。CASTILLA等[11]进行外啮合齿轮泵流场仿真,结果表明提高重合度和使用卸荷槽可以有效减小流量脉动。此外,众多学者通过改变螺旋角、径向间隙、齿数等齿轮的主要参数来减小流量脉动[12]。目前,主要通过增加转子个数和优化转子重要几何参数的方法平抑流量脉动。但是,增加转子个数将导致泵体体积增大、内部结构复杂,制造难度增加;改变几何参数则降低了转子的互换性。
针对非圆齿轮泵大排量导致的流量脉动问题,本文作者提出一种将ADAMS-Simulink联合仿真与CFD(Computation Fluid Dynamics)数值模拟流场仿真相结合的优化方法,以卵形齿轮泵为例展示优化过程,为非圆齿轮泵的流量脉动平抑研究提供新思路。
1 高阶椭圆齿轮泵特性分析
1.1 转子传动特性分析
非圆齿轮泵以一对高阶椭圆齿轮为工作转子。齿轮副节曲线为高阶椭圆,具有封闭节曲线的齿轮副在啮合过程中获得周期性的变速比传动[13]。为设计、制造方便,采用2个相同的高阶椭圆齿轮作为一对共轭齿轮,齿轮副的传动比函数为
(1)
式中:ω1为主动轮的角速度,rad/s;ω2为从动轮的角速度,rad/s;r1、r2分别为主、从动轮的节曲线;k为主、从动轮的偏心率;n为主、从动轮的阶数;θ1为主动轮转角。
高阶椭圆齿轮转子的偏心率和阶数是影响齿轮副传动特性的主要因素。基于控制变量法,分别以同阶数不同偏心率、同偏心率不同阶数的高阶椭圆齿轮副为研究对象,分析传动比随时间的变化规律。图1所示为高阶椭圆齿轮泵转子的传动比曲线。
由图1(a)可知:取偏心率为0.1,当主动轮以恒定角速度转动时,阶数越大则传动比曲线周期越短,频率越快,幅值不变。由图1(b)可知:以二阶椭圆齿轮转子为观察对象,偏心率越大则传动比曲线振幅越大,周期不变。
由式(1)可得从动轮角速度为
(2)
可知:从动轮角速度ω2为主动轮角速度ω1与传动比i12的倒数之积。由于主动轮角速度ω1为定值,则传动比幅值越大,从动轮角速度曲线波动范围越大,传动时振动和冲击越强烈[14]。故在满足工况要求的前提下,为提高转子系统的传动平稳性,应尽量降低工作转子的阶数。
1.2 流量特性分析
以卵形齿轮副(n=2)为工作转子,卵形齿轮泵的工作原理及内部结构与圆齿轮泵相似。当转子按图2所示方向旋转时,上侧啮合的两齿轮相互脱离,形成低压区,下侧两齿轮相互靠拢,形成高压区。油液在大气压的作用下经进油口进入上侧泵腔内,由于两侧的压力差,油液随着齿轮的旋转被带至下侧出油口泵出。图2所示为卵形齿轮泵内部结构示意。
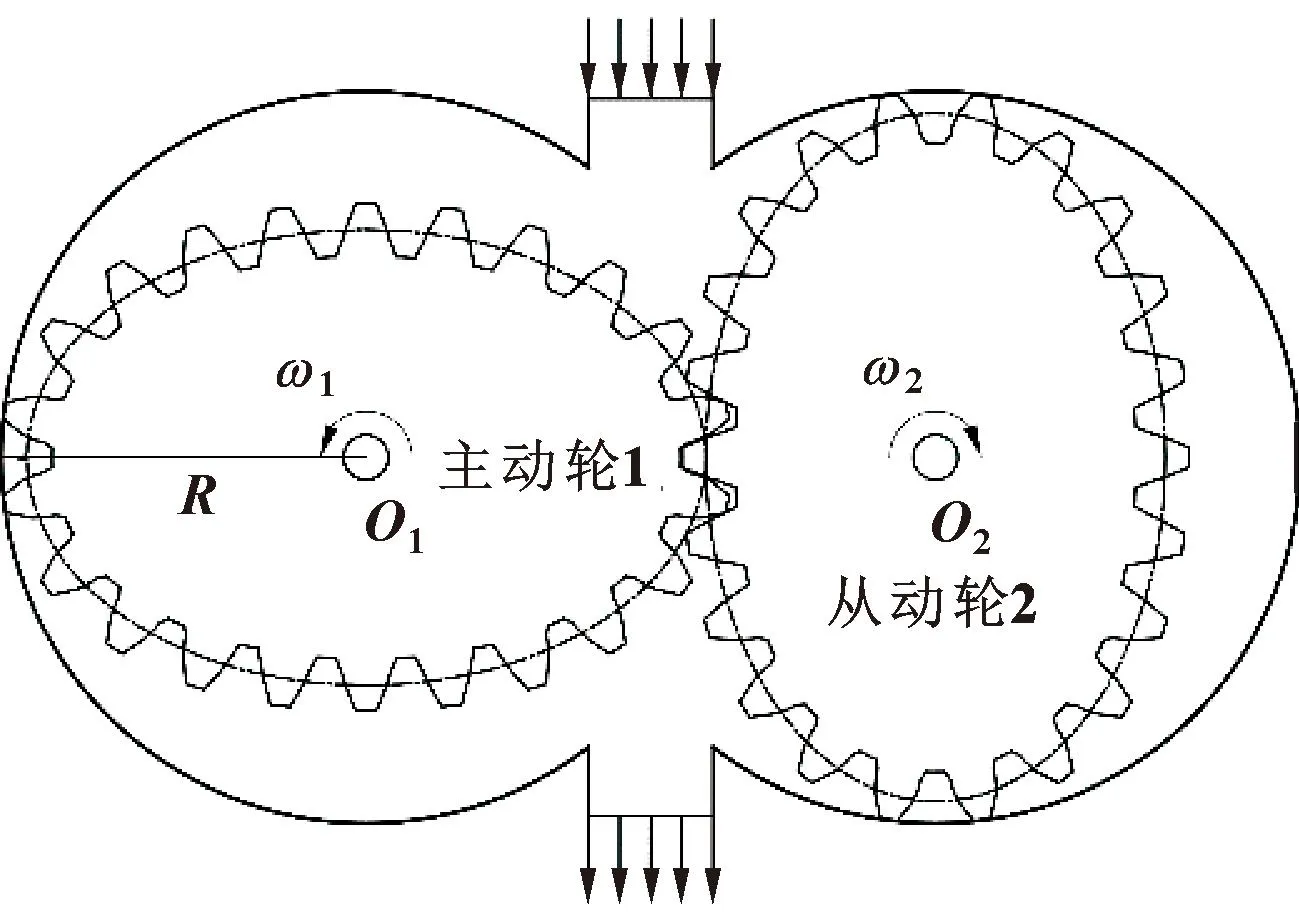
图2 卵形齿轮泵内部结构示意Fig.2 Ovoid gear pump internal structure
卵形齿轮泵的平均流量计算式[15]为
(3)
式中:B为齿宽,mm;a1为中心距O1O2的一半,mm;h为齿顶高,mm。
卵形齿轮泵的瞬时流量计算式为
(4)
卵形齿轮节曲线无内凹条件为:k≤1/3。当k分别为0.1、0.2、0.3时,图3所示为不同偏心率对应的卵形齿轮泵理论瞬时流量曲线。
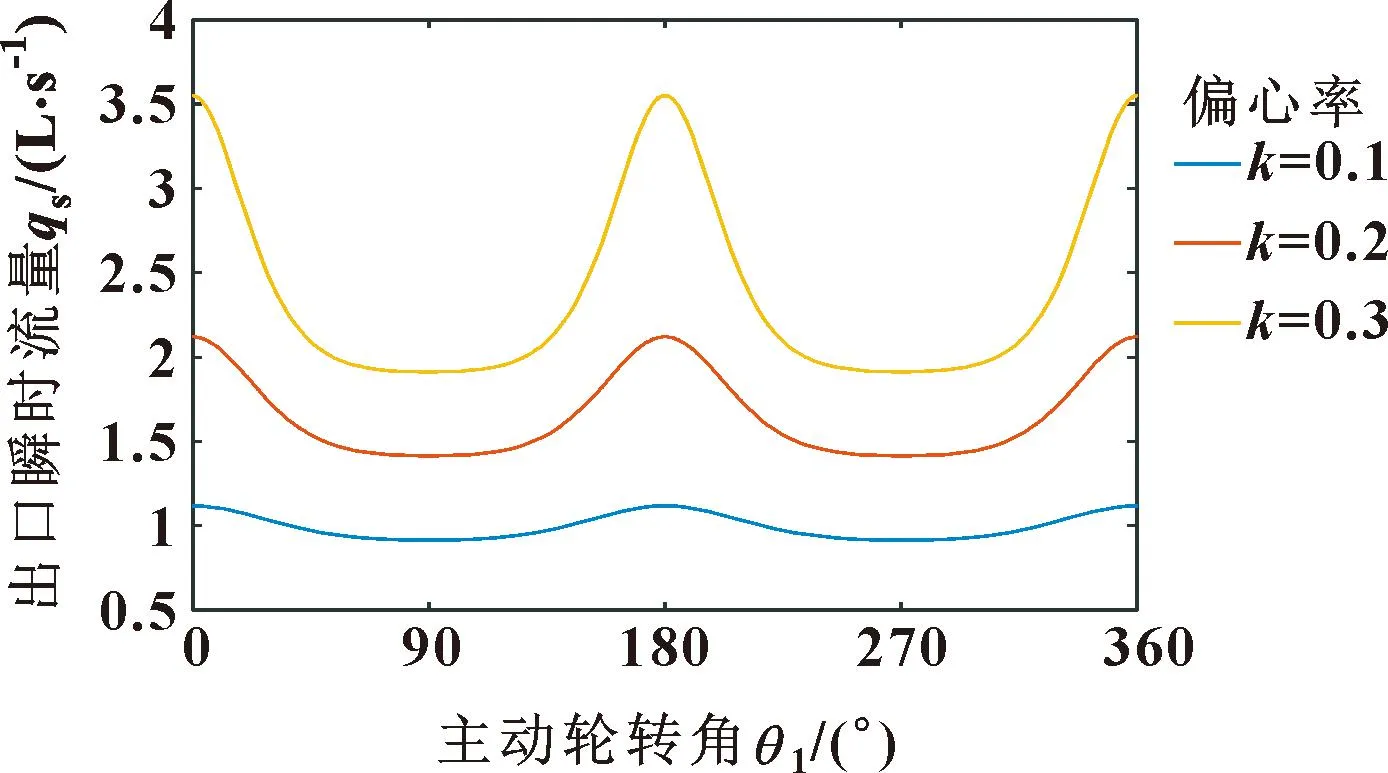
图3 卵形齿轮泵瞬时流量曲线Fig.3 Ovoid gear pump instantaneous flow curves
瞬时流量的不等导致了齿轮泵的流量脉动。由图3可知:转子偏心率越小,齿轮泵的流量脉动越稳定,但泵排量将受到限制。根据转子传动特性,从动轮角速度的幅值波动范围将影响传动的平稳性。偏心率越大,则角速度幅值越大,此时将加大泵的振动和冲击,一定程度上加剧流量脉动。
2 ADAMS与Simulink联合仿真
为兼顾泵的排量及转子传动平稳性,采用ADAMS与MATLAB/Simulink联合仿真技术,以从动轮角速度为观察对象,控制转子角速度变化规律,使传动更为平缓,从而在不改变转子结构的基础上降低流量脉动。
2.1 联合仿真模型
根据前述确定齿轮转子参数如表1所示,基于SolidWorks建立三维模型。

表1 卵形齿轮参数Tab.1 Parameters of ovoid gears
将卵形齿轮三维模型导入ADAMS/View软件模块完成动力学仿真实时调控。为使建立的虚拟样机模型具有与实际情况相近的物理性能,定义其材料、质量、转动惯量等重要属性,建立卵形齿轮副机械系统模型如图4所示。
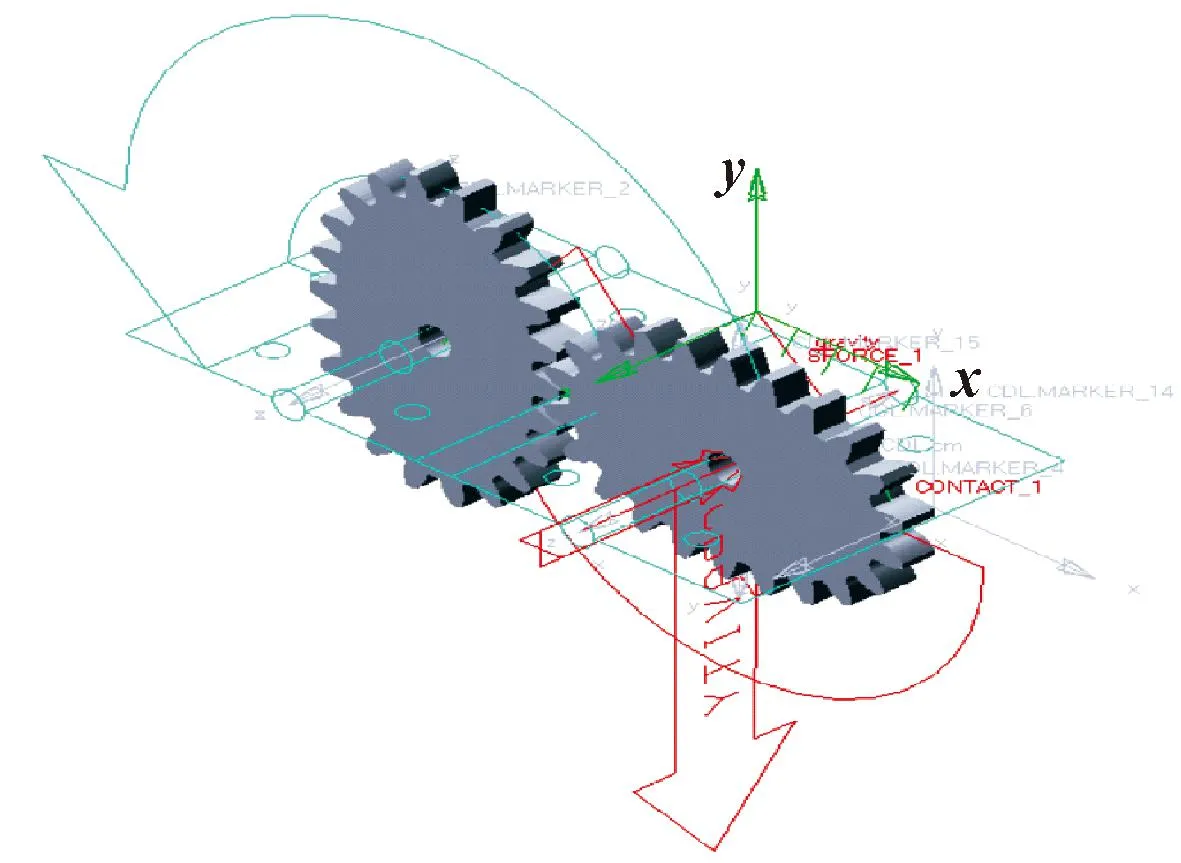
图4 ADAMS/View机械系统模型Fig.4 ADAMS/View mechanical system model
建立变量单元,在ADAMS/Control模块建立机械系统模型与控制系统模型之间的输入、输出接口,以实现数据的实时交互仿真。以主动轮角速度ω1为输入信号变量,从动轮角速度ω2、角加速度为输出信号变量。在Simulink中建立控制模块,并与adams_sub机械系统模型进行集成。随后对Simulink联合仿真控制参数进行设置,其中ADAMS动力学仿真模型为discrete(离散型),仿真方式为interactive(实时交互),可演示相应机械系统的实时仿真动画。联合仿真的交互时间间隔设置为0.001 s,固定步长为0.001 s,仿真计算时间设定为10 s。
2.2 联合仿真结果分析
PID是目前应用最为广泛的一种自动控制算法。其核心是通过整定PID控制器的比例、积分、微分参数以达到最优输出效果[16]。泵转子为卵形齿轮,其运动规律为变速比传动,要使传动过程更加平稳,则采用PID控制器实时控制调节主动轮转速,输入与从动轮的运动规律相反的速度信号。
PID角速度控制器的输出为
(5)
式中:e(t)为反馈偏差;Kp为比例系数;Ki为积分系数;Kd为微分系数。
首先不添加PID控制器,在联合仿真模型的Simulink模块输入主动轮角速度180°/s,启动实时仿真,得到从动轮角速度仿真曲线与理论曲线的对比如图5所示,可以看到联合仿真曲线整体运动规律与理论曲线基本吻合,因此该联合仿真结果具有可靠性。仿真曲线中存在少量脉冲,主要原因是在建模及装配的过程中,卵形齿轮副的2个啮合齿位之间存在一定间隙,使得在啮合传动过程中产生碰撞,导致脉冲。对卵形齿轮的运动学特性分析和脉动优化等方面可忽略此误差的影响。
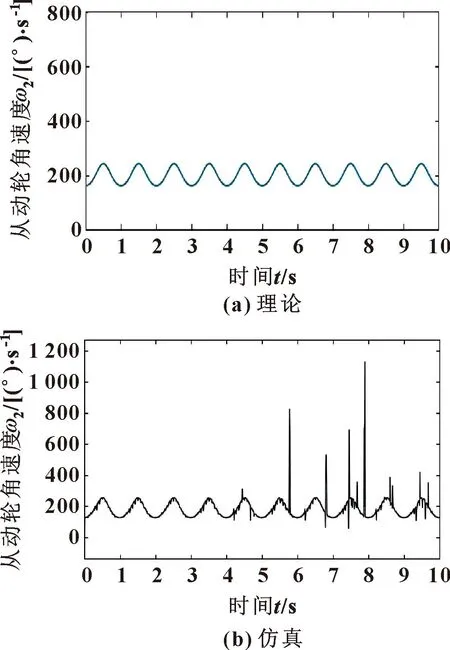
图5 从动轮角速度曲线Fig.5 Angular velocity curves of driven wheel:(a)theory; (b)simulation
添加控制模块,根据输出信号对比例、积分、微分系数不断地进行在线调整,整定出最优参数,从而得到合理的输出结果。联合仿真的控制系统模型如图6所示。
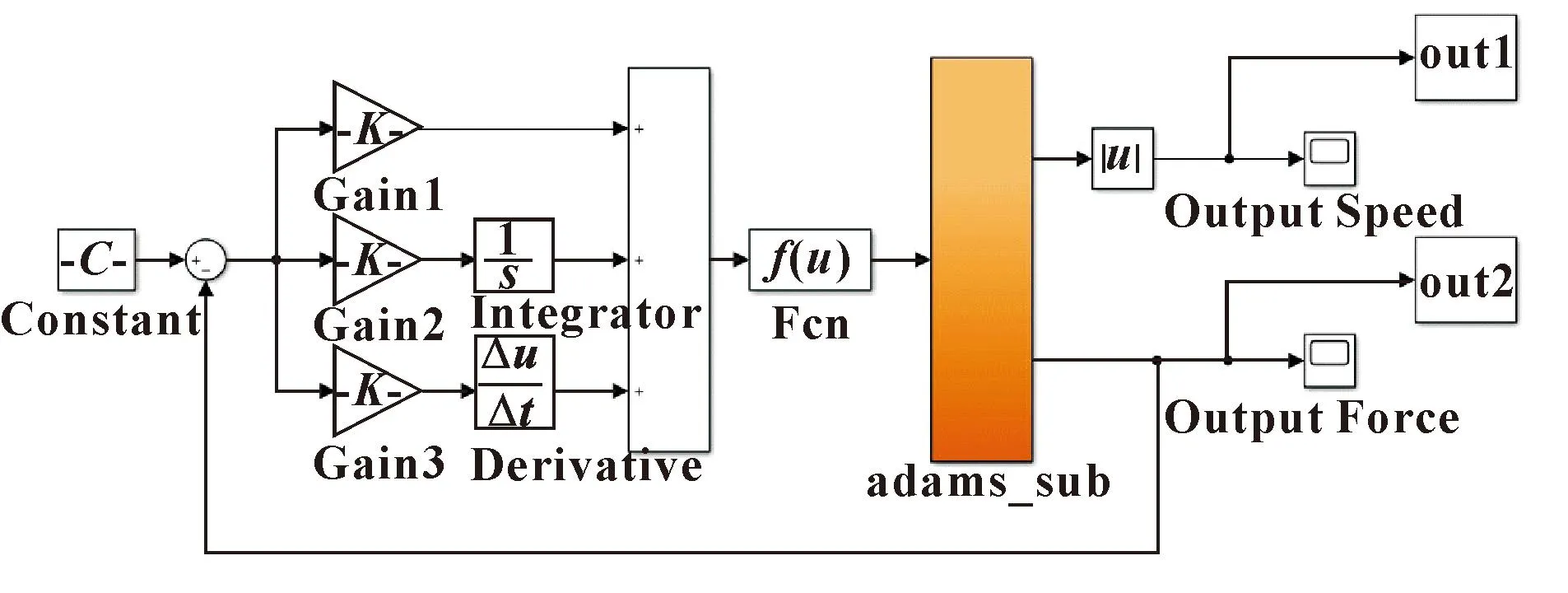
图6 ADAMS-Simulink联合仿真控制系统Fig.6 ADAMS-Simulink co-simulation control system
PID控制器实时调控输入信号,得到控制后的从动轮角速度曲线(如图7所示)仍呈余弦波形式,对比图5可以看到:添加PID控制后幅值波动范围明显减小,周期明显增大,角速度变化频率减小,传动更为平缓,可减轻转子系统的振动。同时,角速度平均值无明显改变,保证转子减振缓冲的同时卵形齿轮泵排量不变。
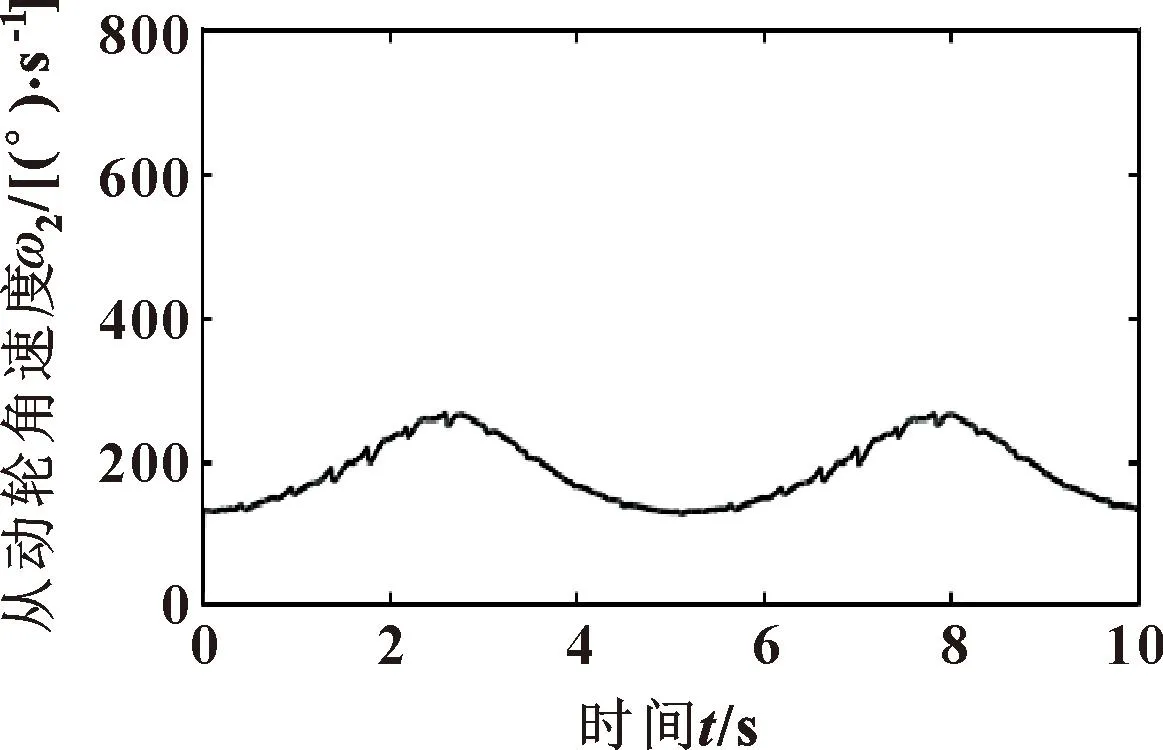
图7 添加PID控制后的从动轮角速度曲线Fig.7 PID controlled angular velocity curve of driven wheel
联合仿真曲线存在微小波动,后期在数据处理过程对曲线进行光滑处理,可忽略此处影响。
3 非圆齿轮泵的流场仿真
3.1 数值模型
对卵形齿轮泵进行CFD数值模拟,需要建立封闭的齿轮啮合流体域,即主从动齿轮的啮合流域形成完整的封闭连通体积[17]。在径向参数不影响仿真试验结果的情况下,采用二维流域模型。卵形齿轮泵网格模型如图8所示,采用非结构化网格划分,对齿顶径向间隙和啮合间隙进行局部网格加密。齿廓曲线啮合处最小间隙为0.03 mm,则视该流域为密封状态。

图8 非圆齿轮泵网格模型Fig.8 Mesh model of non-circular gear pump
采用Navier-Stokes(简称N-S)流动控制方程模拟计算流体流动现象。求解模型选用标准κ-ε湍流模型,压力-速度耦合方程采用Simple算法进行求解[18]。标准κ-ε模型是一种高雷诺数模型,在旋转类型的液压泵中,流体介质类型决定了质点的速度和压力,因此需要在高雷诺数下计算有效液体黏度的湍流模型。根据实际工况,齿轮泵计算域的进口边界条件为压力入口,设置为一个标准大气压;出口边界条件为压力出口,设置为2.5 MPa。齿轮泵内流动介质密度设置为880 kg/m3,黏性系数为1.008 7×10-3Pa·s。
由于复杂的边界条件难以直接输入给Fluent,因此需要通过用户自定义函数功能(User Define Function,UDF)扩展功能。定义各齿轮齿廓为运动边界,使用UDF函数设定,程序如下:
#include "udf.h"
DEFINE_CG_MOTION(gear1_motion,dt,vel,omega,time,dtime)
{omega[2]= 3.141592654;}
DEFINE_CG_MOTION(gear2_motion,dt,vel,omega,time,dtime)
{omega[2]=-3.141592654* (1-0.2*0.2)/(1+0.2*0.2-2*0.2*cos(2*3.141592654*time));}
转子旋转45°时卵形齿轮泵内部流速云图如图9所示。
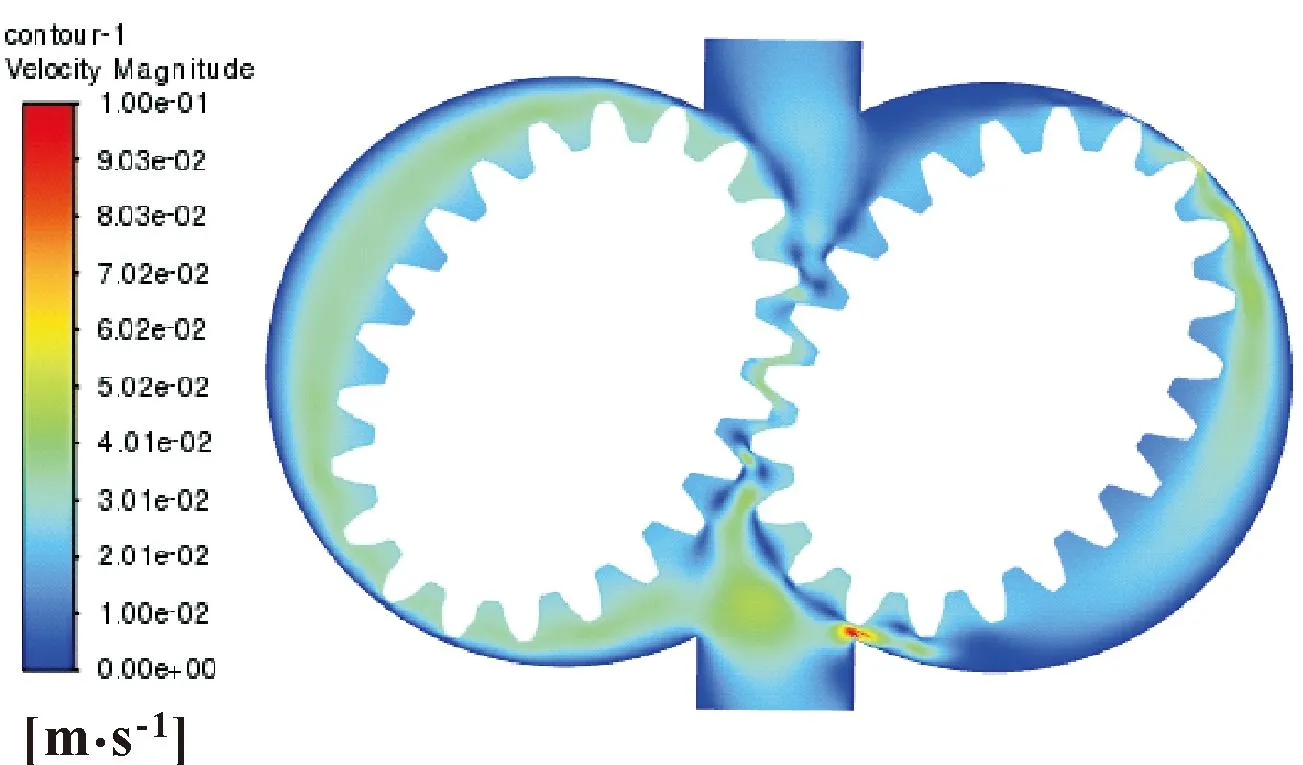
图9 转子旋转45°时卵形齿轮泵内部流速云图Fig.9 Internal flow velocity cloud map of ovoid gear pump with rotor rotation 45°
动网格模型重构方法采用弹性光顺法和局部网格重构法,添加出口流量监测,对流场仿真模型进行瞬态计算得到齿轮泵出口瞬时流量,与式(4)计算得到的理论瞬时流量曲线对比如图10所示,可以看到流量逐渐稳定后其变化规律基本一致。
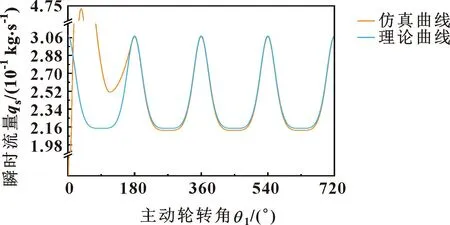
图10 仿真瞬时流量与理论瞬时流量曲线Fig.10 Simulation instantaneous flow rate and theoretical instantaneous flow rate curves
3.2 优化结果分析
由于Fluent与Simulink没有直接的数据交互接口,为精确模拟PID控制器控制后流场中的转子变速比传动关系,验证该方案的脉动平抑效果,将控制后的齿轮副角速度参数导出,使用Visual Studio平台进行C编译,作为瞬态模型的运动边界条件在Fluent中调用,实现Simulink与Fluent数据耦合。部分程序如下:
DEFINE_CG_MOTION(gear1_motion,dt,vel,omega,time,dtime)
{int ndelT,nT;
real ndel,v;
nT=time/T;
time=time-nT*T;
ndelT=time/delT;
ndel=ndelT*delT;
v=get_v_from_dat(ndel);
omega[2]=v*M_PI/180*(1+k*k-2*k*cos(2*phi))/(1-k*k);
phi+=v*M_PI/180*(1+k*k-2*k*cos(2*phi))/(1-k*k)*dtime;}
DEFINE_CG_MOTION(gear2_motion,dt,vel,omega,time,dtime)
{int ndelT,nT;
real ndel,v;
nT=time/T;
time=time-nT*T;
ndelT=time/delT;
ndel=ndelT*delT;
v=get_v_from_dat(ndel);
omega[2]=-v*M_PI/180;}
图11所示为平抑前后的瞬时流量曲线,可以看出:平抑后流量幅值明显降低,曲线脉动更为平稳,同时平均流量没有明显改变。
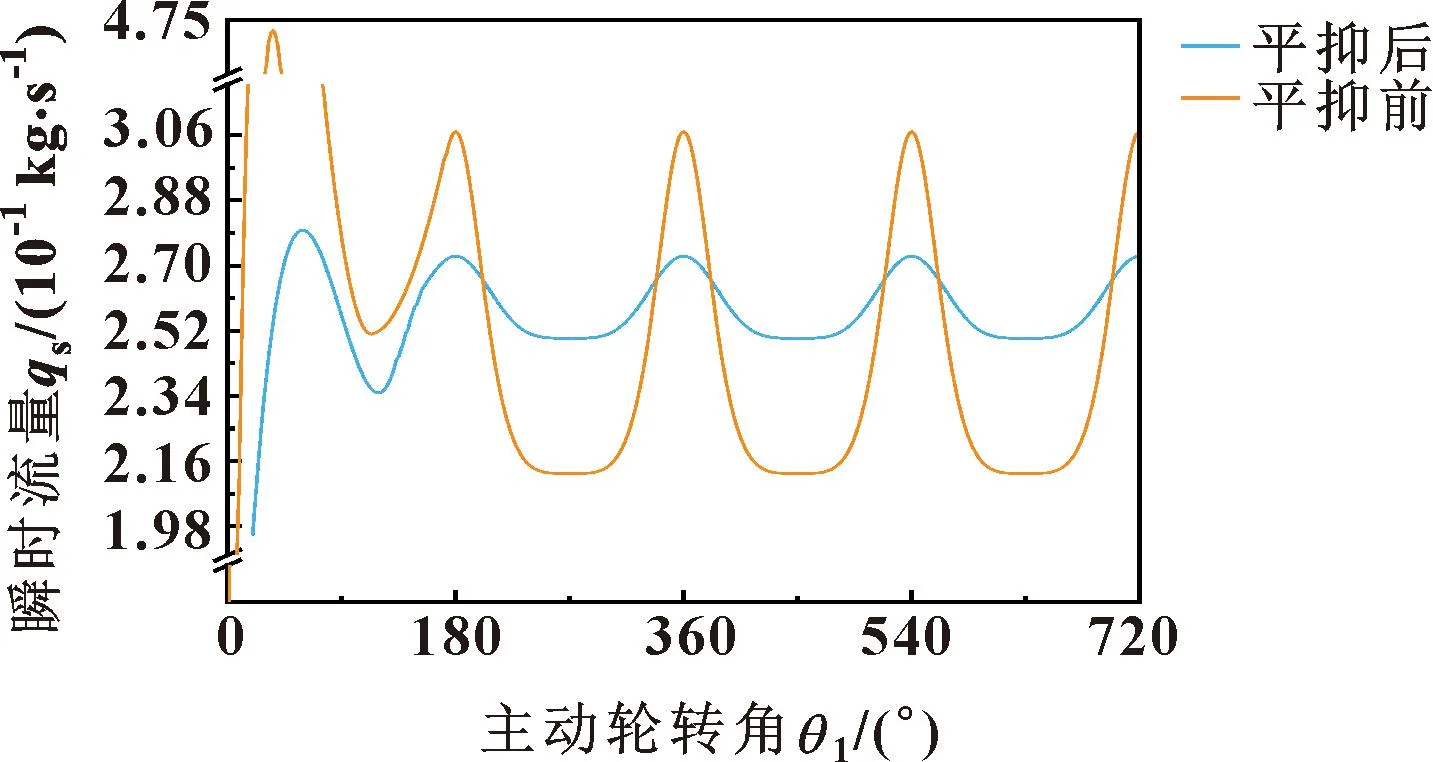
图11 平抑前后齿轮泵出口瞬时流量对比Fig.11 Comparison of instantaneous flow at the outlet of gear pump before and after flattening
引入流量脉动率σ作为流量脉动的评价指标:
(6)
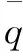
将图10瞬时流量曲线数值代入式(6)中,得到平抑前的流量脉动率为σ1=(3.069 92-2.126 07)/2.390 11=39.489 8%;平抑后的流量脉动率为σ2=(2.725 49-2.499 3)/2.579 76=8.767 9%,相较平抑前下降了约30.72%,流量波动得到明显的改善。
4 结论
(1)通过理论分析得出高阶椭圆齿轮泵转子的传动特性,影响转子传动平稳性的主要因素为偏心率及其阶数。
(2)以卵形齿轮泵为研究对象分析其流量特性,得出瞬时流量脉动与偏心率的关系;基于Fluent动网格技术实现数值模拟,验证了卵形齿轮泵的瞬时流量脉动规律与理论值相符合。
(3)提出一种基于ADAMS与Simulink联合仿真实现齿轮泵转子的平稳传动、缓冲减振,从而减小齿轮泵流量脉动的方法;联合仿真方法有效降低了齿轮转子传动时产生的振动和冲击。
(4)基于Visual Studio实现Simulink与Fluent 的数据耦合。Fluent数值模拟结果表明:卵形齿轮泵转子平稳传动后的流量脉动率下降了约30.72%,该方法可在不改变齿轮泵内部结构的情况下平抑流量脉动。
