冲击荷载下钢筋混凝土梁抗冲击性能研究进展
2024-01-12张晓燕杨涛春王银谢群陈文文
张晓燕 杨涛春 王银 谢群 陈文文


文章编号:1671-3559(2024)01-0037-11DOI:10.13349/j.cnki.jdxbn.20230524.001
摘要:针对冲击荷载下钢筋混凝土梁抗冲击性能研究广泛并取得许多有价值成果的研究现状,对国内外众多学者基于试验、数值与理论等方法开展的大量工作与研究成果进行综述,包括冲击荷载的研究、材料的应变率效应、钢筋混凝土梁的动态响应与破坏机制、设计评估方法;根据钢筋混凝土梁破坏规律与特点,对破坏模式进行归纳总结,并提出基于承载力的破坏模式判别准则;指出未来钢筋混凝土梁抗冲击研究重点应包括冲击荷载的计算、钢筋混凝土梁破坏判别与简化响应计算。
关键词:冲击荷载;破坏模式;动态响应;钢筋混凝土梁;评估方法
中图分类号:TU375.1
文献标志码:A
开放科学识别码(OSID码):
Research Review on Impact Resistance of
Reinforced Concrete Beams Under Impact Loads
ZHANG Xiaoyan1, YANG Taochun1, WANG Yin1, 2, XIE Qun1, CHEN Wenwen1
(1. School of Civil Engineering and Architecture, University of Jinan, Jinan 250022, Shandong, China;
2. State Key Laboratory of Disaster Prevention and Mitigation of Explosion and Impact,
Army Engineering University of Peoples Liberation Army of China, Nanjing 210007, Jiangsu, China)
Abstract: Aiming at the status of research on impact resistance of reinforced concrete beams under impact loads, extensive research and many valuable achievements having been made, a large amount of work and research results based on experimental, numerical, and theoretical methods carried out by many scholars at home and abroad were summarized, including the research on impact loads, strain rate effect of materials, as well as dynamic response, failure mechanism, and design assessment methods of reinforced concrete beams. According to the failure law and characteristics of reinforced concrete beams, the failure modes were summarized, and the criterion of failure mode discrimination based on bearing capacity was proposed. The future research emphasis for impact resistance of reinforced concrete beams was pointed out to be the calculation of impact loads, failure discrimination of reinforced concrete beams, and simplified response calculation.
Keywords: impact load; failure mode; dynamic response; reinforced concrete beam; assessment method
鋼筋混凝土(RC)结构在正常服役过程中可能遭受爆炸冲击、车辆撞击、船舶碰撞及海浪冲击等各类冲击作用,从而引起严重的结构损伤或破坏,甚至导致灾难性后果。作为RC结构中的最基本构件,RC梁的抗冲击性能至关重要,也是当前工程研究的热点与重点课题。
针对RC梁在冲击荷载下的抗冲击性能,研究人员通过大量试验[1-2]与数值模拟[3-5]发现,RC梁在
收稿日期:2022-09-25 网络首发时间:2023-05-25T15:20:05
基金项目:国家自然科学基金项目(52178515)
第一作者简介:张晓燕(1997—),女,山东滨州人。硕士研究生,研究方向为结构工程。E-mail: 1936665667@qq.com。
通信作者简介:杨涛春(1983—),男,山东青州人。副教授,博士,硕士生导师,研究方向为爆炸灾害分析评估。E-mail: yangtaochun@126.com。
网络首发地址:https://kns.cnki.net/kcms2/detail/37.1378.N.20230524.1632.002.html
冲击荷载、静载条件下的行为存在明显差异,跨中承受单点冲击的简支梁的峰值接触力远大于相应的静态承载能力,并且冲击荷载下裂缝的分布集中在加载点附近[6]。上述差异的原因主要归结于冲击荷载的瞬态特性[7-8]、钢筋与混凝土材料的应变率敏感性[9-12]、构件的惯性效应[13-15],以及混凝土材料的多相复合特性。
在冲击荷载下,RC梁包括2个响应阶段:1)冲击后的短时间内。在加载点处产生应力波,从而引起构件的局部响应。 2)后续的较长时间内。构件发生弹塑性变形,从而引起整体响应与破坏。目前,整体破坏研究是RC梁在冲击荷载下相关研究的主要课题,而局部破坏如侵彻、贯穿或冲切是RC板在冲击荷载下的主要破坏模式[16-18]。
在冲击荷载下, 随着变形的增大, RC梁损伤程度逐渐从无损伤、轻微损伤、中等损伤、严重损伤直至破坏, 因此很多学者通过研究建立了RC梁的最大变形与损伤程度的关系[19-20]。 除了变形以外, RC梁的抗弯、抗剪承载力也是研究RC梁破坏损伤与安全性的重要方向, 但是目前尚未得到充分研究[21]。
目前有关RC梁的抗冲击性能研究主要是通过试验研究、数值模拟与理论分析等方法,深入开展RC梁的冲击破坏机制、响应过程与破坏特征、设计评估方法等的广泛研究,并取得许多有价值的成果。本文中主要针对冲击荷载下RC梁性能的已有研究进行综述,分析RC梁抗冲击性能的相关研究进展,主要包括冲击荷载的研究、材料的应变率效应、RC梁的动态响应与破坏模式、设计评估方法等,并提出RC梁破坏模式的判别准则与流程。
1 冲击荷载
1.1 形式
冲击荷载峰高持续时间短, 在冲击试验中施加与控制较难, 同时, 受結构动力特性的影响, 冲击试验与静载试验存在很大区別, 目前常用液压试验机与落锤试验机作为动力加载装置。 在落锤冲击试验中, 在锤头位置或梁锤接触区域安装压力传感装置, 从而获取冲击力时程曲线。 不同冲击荷载下的冲击力时程曲线不同[22]:随着冲击高度的增加, 冲击力峰值增大, 并且达到峰值的时间逐渐缩短;不同冲击荷载下冲击力的振荡变化趋势相似, 但是冲击速度越大, 冲击振荡频率越高, 脉冲波持续时间越短,冲击力峰值越大。
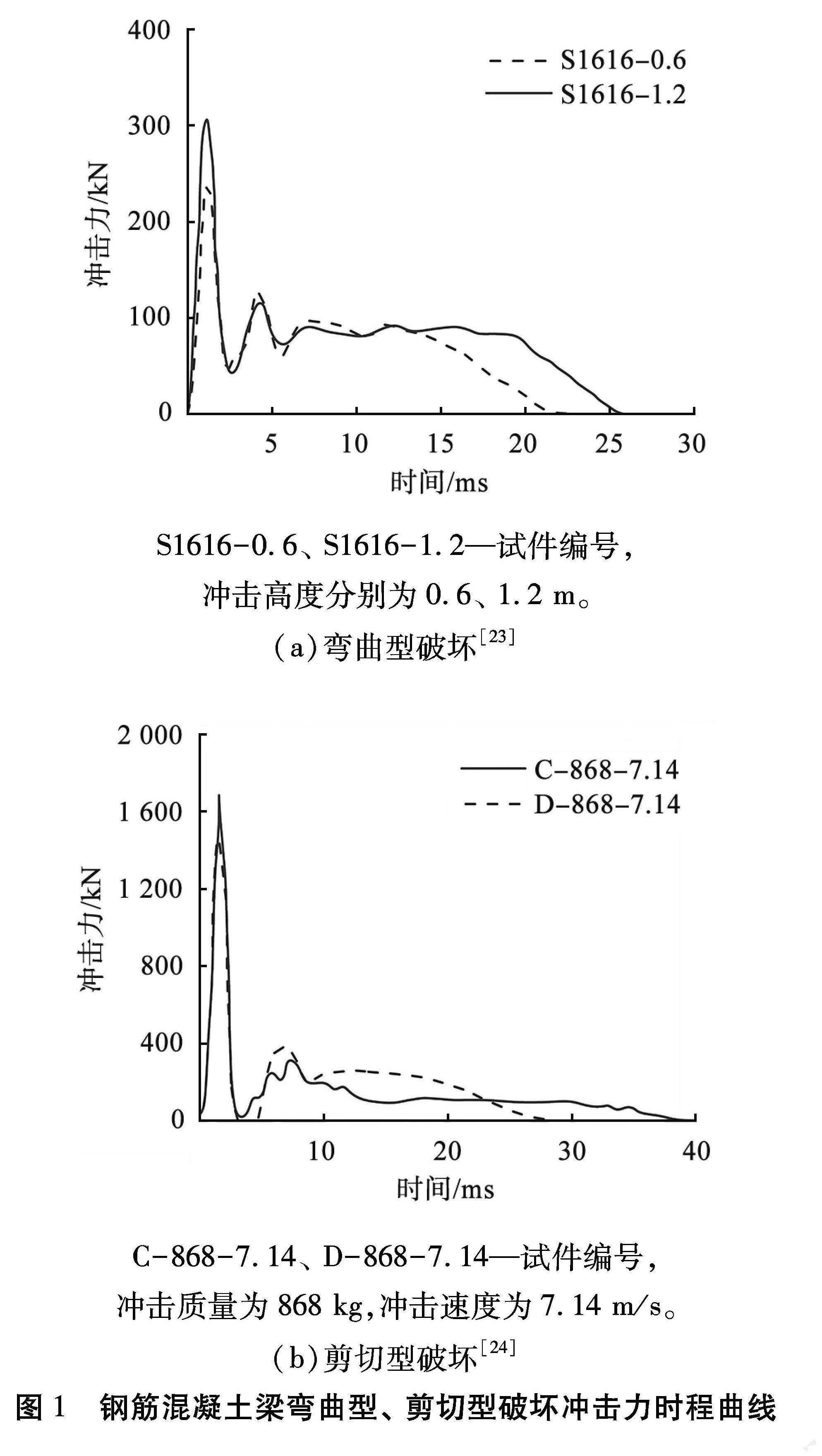
引起RC梁不同破坏模式的冲击力时程曲线也存在差异。 RC梁弯曲型破坏[23]、剪切型破坏[24]冲击力时程曲线如图1所示。 由图1(a)可知:产生弯曲破坏的RC梁的冲击力在初始阶段迅速增至峰值点, 冲击力时程曲线由2个正弦半波组成,即峰高持续时间短的峰值波、峰高持续时间长但峰值较小的主波。 经短暂振荡后冲击力逐渐趋于平稳, 并进入持续时间较长的平台期, 直至冲击体即落锤动能消耗完毕, 冲击力衰减至0, 冲击过程结束。 由图1(b)可知:产生剪切破坏的RC梁的冲击力在短时间内增至峰值, 然后迅速减小, 形成第1个波形, 峰值波和主波间可能出现次生峰值波。 经短暂振荡后, 直接出现较长的卸载段, 冲击体动能消耗完毕, 冲击力衰减至0, 冲击过程结束。 发生剪切破坏的梁冲击力时程曲线经历振荡后发生卸载而不经历稳定的平台期, 同时, 试验研究[24]表明, RC梁跨度越大则对振荡频率的影响越明显。
1.2 计算方法
通常采用等效静力法和动力分析方法[25]计算结构受到的冲击荷载。等效静力法通过对大量试验并结合工程实际经验进行分析,采用动态放大系数计算冲击荷载,因简便、实用而被欧洲建筑工程设计规范[26]采纳。
对于冲击重力为G、冲击高度为h的自由落体冲击[27],根据能量守恒,可得
G(h+Δ)=12kΔ2 ,(1)
式中:Δ为冲击过程中产生的最大位移;k为刚度。 被冲击物在静态负荷下的位移为Δst=G/k, 可以得到
Δ2-2ΔstΔ-2Δsth=0 ,(2)
解得Δ=Δst1+1+2h/Δst。对该解的左、右两边乘以刚度k,得到
Pd=G1+1+2h/Δst ,(3)
式中Pd=kΔ为冲击荷载。由此,动态放大系数Kd=1+1+2h/Δst,当h趋于0时,动态放大系数为欧洲建筑工程设计规范[26]中推荐的2。除此之外,也可以采用赫兹接触理论对冲击接触力进行预测[28],即
P=Kμ3/2 ,(4)
式中:P为接触力;K为接触系数;μ为接触变形。
等效静力法在一定程度上可以预测冲击荷载,但是得到的等效静载与动载相比可能存在较大误差,并且实际的冲击过程是一个复杂的非线性动力学过程,该方法忽略了结构自身的动态响应[29]。Abrate[30]认为,RC梁在承受冲击荷载时,接触区域局部变形相较于整体变形可忽略不计,提出最大冲击力F的预测公式,即
F=vc(kmc)1/2 ,(5)
式中:vc为冲击速度;mc为冲击质量。 相对于等效静力法, 式(5)考虑更充分, 但是相关研究较少, 无法直接服务于RC结构抗冲击设计, 有待进一步研究。
2 应变率效应
2.1 动力荷载下RC构件的应变率
静力、动力荷载下RC构件力学性能有较大区别,主要是由动力荷载作用下材料的应变率效应导致的,而混凝土和钢筋均属于应变率敏感性材料,混凝土与钢筋材料在冲击荷载下的动态强度均大于静态强度[31]。
受不同加载方式的影响,RC构件的应变率存在明显差异,不同荷载作用下RC构件应变率如表1[32]所示。
RC构件在不同的试验加载装置条件下可以获得不同的应变率。液压设备可以获得1 s-1量级的应变率[33],落锤装置可以获得10 s-1量级的应变率[34],霍普金森杆装置可以获得10~103 s-1量级的应变率[35]。部分研究者提出了应变率的估算公式,如Adhikary等[36]提出的应变率ε·计算公式为
ε·=1.25v0.82 ,(6)
式中v为加载速率。
2.2 钢筋的应变率效应
描述应变率效应对钢筋影响的典型模型包括Johnson-Cook模型[37]和Cowper-Symonds模型[38]。
Johnson-Cook模型为
σ=(A+Bεn)(1+Cln ε·*)(1-Tm) ,(7)
式中:σ为应力;ε为塑性应变;ε·*=ε·/ε·0为塑性应变率,准静态应变率ε·0=1.0 s-1;T为温度;A、B、C、n、m为材料常数。式(7)中不同的部分描述了不同的材料效应,其中1+Cln ε·*反映了应变率效应对钢筋行为的影响。
Cowper-Symonds模型适用于描述钢筋在低应变率时的力学性能,模型为
σd/σs=1+(ε·/D)1/p ,(8)
式中:σd、σs分别为材料在动力、静力荷载下的应力;D、p分别为与材料类型、应变强化相关的参数。
2.3 混凝土的应变率效应
动态强度增大系数(DIF)为动态、静态强度之比,被视为一种材料特性,用于考虑应变率效应的影响。考虑冲击荷载下应变率效应对混凝土材料的影响,欧洲混凝土协会(CEB)[39]推荐的混凝土受压DIF为
cDIF=fcd/fcs=(ε·/ε·cs)1.026η, ε·≤30 s-1 ,
λ(ε·/ε·cs)1/3,ε·>30 s-1 ,(9)
式中:fcd、fcs分别为动态、 静态抗压强度;参考抗压应变率ε·cs=3×10-5 s-1;lg λ=6.156η-2, η=(5+9fcs/fco)-1;参考抗压强度fco=10 MPa。混凝土受拉DIF为
tDIF=ftd/fts=(ε·/ε·ts)1.016χ, ε·≤30 s-1 ,
β(ε·/ε·ts)1/3,ε·>30 s-1 ,(10)
式中:ftd、fts分别为动态、静态抗拉强度;参考抗拉应变率ε·ts=3×10-6 s-1;lg β=7.11χ-2.33, χ=(10+6fcs/fco)-1。
尽管CEB推荐的DIF计算公式被广泛使用,但是计算结果与试验数据误差较大。Malvar等[40]基于大量试验数据对式(10)进行修正,修正的混凝土受拉DIF为
tDIF=ftd/fts=(ε·/ε·ts)χ, ε·≤1 s-1 ,
β(ε·/ε·ts)1/3,ε·>1 s-1 ,(11)
其中ε·ts=10-6 s-1, lg β=6 χ-2, χ=(1+8fcs/fco)-1。
Hao等[41]从CEB推荐的DIF关系式中去除结构效应中横向惯性效应对DIF的贡献,依据试验数据推导出了真实的混凝土材料应变率DIF,即
cDIF=fcd/fcs=0.041 9 lg ε·+1.2165, ε·≤30 s-1 ,
0.898 8 lg2 ε·-2.825 5 lg ε·+
3.490 7,ε·>30 s-1 ,(12)
tDIF=ftd/fts=0.26 lg ε·+2.06, ε·≤1 s-1 ,
2 lg ε·+2.06,1 s-1<ε·≤2 s-1 ,
1.443 31 lg ε·+2.227 6,
2 s-1<ε·≤150 s-1 。
(13)
3 冲击荷载下RC梁的动态响应
3.1 破坏特点及影响因素
RC梁在冲击荷载下的破坏模式分为3种:1)弯曲破坏。由梁内纵向受拉钢筋屈服控制,破坏时延性较好。 2)弯剪破坏。梁出现剪切破坏特征的同时弯曲裂缝发展显著,为2种不同破坏响应特征的耦合,破坏发生机制较复杂。 3)剪切破坏。由剪切斜裂缝控制的脆性破坏。
RC梁跨中冲击試验表明,冲击速度、冲击能量、纵筋配筋率与配箍率、混凝土强度、梁的截面尺寸、剪跨比等因素均会影响RC梁的承载能力和破坏模式[42-46],其中冲击速度是影响RC梁破坏模式的关键因素[47-48]。随着冲击速度的增大,RC梁由弯曲破坏向剪切破坏转变。高速冲击下发生剪切破坏的RC梁纵向受拉钢筋未能充分发挥作用[49],而箍筋作用明显,合适配箍的梁裂缝分布更均匀,箍筋影响了RC梁的裂缝形态[50]。低速冲击下发生弯曲破坏的RC梁提高受拉钢筋的配筋率能够增强梁的承载能力[51-52],但是相对于高配筋率的RC梁,除了整体的变形与破坏外,梁锤接触区域还出现明显的局部破坏[23]。
在快速加载条件下, RC梁的极限强度增大, 但是延性劣化, 加载速率的增大导致构件破坏模式改变[53]。 原因是在高应变率条件下, 混凝土强度增大, 同时, 混凝土与钢筋黏结性能改善, 由于截面上存在较大的应力分布梯度, 因此钢筋承受了过多的集中应力, 使钢筋过早失效, 劣化了构件的延性[54]。 随着冲击速度的增大, RC梁破坏模式变化, 并且破坏向冲击点附近集中。 在不同的冲击速度条件下, 存在不同的机制控制RC梁的响应:微裂缝的末端局部惯性效应在冲击速度较小时控制梁的响应, 而结构的惯性效应在冲击速度较大时控制梁的响应[49]。 综上, 受应变率效应和惯性效应的共同影响, RC梁在冲击荷载下的响应十分复杂。
RC梁在冲击荷载下的破坏与RC梁在静载下的行为也有密切联系。静载下发生弯曲破坏的梁在不同冲击荷载下发生破坏模式转变,而静载下发生剪切破坏的梁在冲击荷载下未发生破坏模式变化[55-57]。剪切效应在局部响应阶段较显著[58],冲击后很短时间内,冲击荷载作用区域产生局部应力峰值,此时应力波尚未在整个结构传播,梁所承受的剪力集中于冲击作用区域,从而引起剪切斜裂缝的出现,局部阶段的响应对RC梁破坏模式的改变影响显著;随后应力波在整个结构分布均匀,RC梁发生整体响应与变形。局部响应与整体响应的竞争性影响使得在静载下发生弯曲破坏的RC梁在冲击荷载下可能发生弯曲破坏向剪切破坏的转变,在静载下发生剪切破坏的RC梁在冲击荷载下仍发生剪切破坏[59]。
3.2 抗弯与抗剪性能
RC梁在满足强度设计要求的前提下,延性弯曲破坏为破坏形式的首选。在静载作用下,现有设计理论和方法对RC构件的性能把握较充分,能很好地实现梁的延性破坏,但是对于冲击荷载下RC构件抗弯与抗剪性能,还需要进一步研究。
无论在静载下还是在动载下,RC梁的弯曲损伤破坏都与RC梁的最大变形响应存在直接关系。岸德光等[60]定义弯曲破坏的极限状态为残余变形大于净跨的1.1%。考虑弯曲破坏时,最大塑性变形通常出现在跨中,Krauthammer[19]采用跨中挠度与半跨的比值作为弯曲破坏的界限,并认为随着变形的增大,RC梁损伤程度从无损伤、轻微损伤、中等损伤、严重损伤直至破坏。除变形之外,RC梁的抗冲击承载力也是研究其破坏损伤的重要方向。目前,冲击荷载下构件的承载力通常采用冲击力最大值或支座反力最大值进行表述。试验[14]表明,冲击力在达到最大值时基本上被惯性力所抵抗,RC梁整体变形很小,没有造成局部破坏以外的较大损伤,因此采用最大冲击力表述梁的抗冲击承载力并不合适。Soleimani[61]与Kishi等[62]开展了RC梁落锤冲击试验,通过对比分析认为,相较于冲击力最大值,支座反力最大值可以更合理地评估梁的抗冲击承载能力;但仍有部分研究者对此提出质疑[43],因此最大支座反力能否真实反应梁的抗冲击性能有待进一步论证。
静载时RC梁的抗剪性能通常通过无腹筋与配箍RC梁分别进行研究。曾翔等[6]、许斌等[43]为了研究RC梁在冲击荷载下的抗剪性能,分别完成了无腹筋与配箍RC梁的冲击试验,发现合适的配箍率能抑制剪跨内裂缝的发展,随着冲击荷载的增大,RC梁斜裂缝数量减少并呈向跨中集中的趋势,冲击点两侧的斜裂缝最终成为主要的剪切破坏面。研究[44,63]表明,RC梁在冲击荷载下易发生剪切破坏,并且无论RC梁最终发生弯曲破坏还是剪切破坏,跨中区域都会有对角剪切裂缝产生。静载下满足抗弯设计的梁在冲击试验中也出现严重的剪切斜裂缝[64],在冲击点下形成剪切楔,因此可以证明剪切破坏机制在结构响应中发挥重要作用。
虽然各国学者对冲击荷载下RC梁剪切破坏的机制认识尚不充分,但是已有试验[65]表明,RC构件在冲击响应初期就发生了直剪型破坏,即构件在发生弯曲响应之前就发生了直剪破坏;也可以认为发生弯曲破坏的构件在冲击响应初期经历了直剪响应,但是未达到极限状态而造成直剪破坏。阎石[66]、师燕超等[67]通过数值模拟对RC构件直剪破坏动力响应进行了研究,发现增加配箍率可以增强构件的抗冲击能力。目前关于冲击荷载下RC梁抗弯与抗剪性能的研究尚不能达到延性设计的要求,相关研究仍需要继续深入开展。
4 冲击荷载下RC梁的破坏模式
4.1 破坏模式分类
RC梁在冲击荷载下随着冲击速度的增大会发生破坏模式转变。根据已有RC梁的跨中冲击试验研究,RC梁在冲击荷载下的裂缝发展规律及破坏形态特征如下。
4.1.1 弯曲破坏
当冲击速度较小时,RC梁跨中部位存在若干条垂直弯曲裂缝,斜裂缝数量较少,梁内纵向受拉钢筋屈服,梁体变形达到弯曲极限破坏限值,RC梁发生弯曲破坏[24]。
在冲击初始阶段,梁体在跨中冲击点区域出现倾角为45°的斜裂缝,起始于梁底面的垂直弯曲裂缝也随之出现,垂直裂缝的出现时间一般稍晚于斜裂缝的。随后在跨中与支座间的剪跨区出现斜裂缝,同时弯曲裂缝沿梁的高度方向垂直扩展。随着时间的推移,梁跨中弯曲裂缝宽度明显增大,数目增多,已有斜裂缝发展不明显,不再有新的斜裂缝出现。随着梁体变形的增大,垂直裂缝成为主要破坏裂缝,RC梁发生弯曲破坏。冲击荷载下RC梁的弯曲破坏模式如图2[24]所示。
4.1.2 弯剪破坏
随着冲击速度的增大,RC梁跨中与剪跨区斜裂缝发展,出现剪切破坏特征,同时垂直弯曲裂缝发展明显,梁体整体延性较好,发生弯剪破坏[68]。相对于弯曲破坏,弯剪破坏中弯曲变形的比例减少,而剪切响应比例增加。
在落锤冲击荷载下,RC梁跨中弯曲裂缝发展,冲击点两侧也有明显斜裂缝出现,裂缝从冲击点位置向下沿对角线扩展到梁底面位置。此后,弯曲裂缝集中于跨中区域;而斜裂缝在跨中与支座附近均有分布,除了跨中区域从梁顶至梁底产生的2条对角斜裂缝,同时存在从支座处向跨中方向延伸的对称裂缝,如图3[68]所示。从图中可以看出,整个试件的剪切斜裂缝与弯曲裂缝均发展明显,梁体分布较多微裂紋,箍筋作用明显,RC梁呈现弯剪破坏形态。
4.1.3 剪切破坏
静载弯曲破坏的RC梁在高速冲击下的剪切裂缝发展为主要破坏裂缝,RC梁发生剪切破坏。
当冲击速度较小时,冲击点位置两侧对角斜裂缝发展明显,成为主要裂缝,剪跨区有斜裂缝分布并呈向跨中集中趋势, 跨中部分弯曲裂缝贯穿梁截面, 如图4(a)[68]所示,
破坏进一步发展,跨中斜裂缝从梁顶贯穿到梁底发展成剪切破坏面。当冲击速度较大时,跨中区域斜裂缝从冲击点直接向下发展,形成最终的剪切破坏面[23],如图4(b)[24]所示,此时剪跨区及支座处斜裂缝不再发展。
静载剪切破坏的RC梁在低速冲击下未发生破坏时存在典型的弯曲响应,在高速冲击下直接发生剪切破坏[69]。
在低速冲击下, RC梁跨中自底面形成多条弯曲裂缝, 剪跨区斜裂缝对称发展, 分布较均匀, 如图5(a)[69]所示。从图中可以看出,冲击结束后,RC梁的残余挠度微小,未发生破坏。高速冲击下的梁在跨中冲击点区域形成明显的楔形斜裂缝,在冲击速度达到一定值后,冲击点两侧的斜裂缝形成最终剪切破坏面,如图5(b)[69]所示。
4.2 破坏模式判别方法
在冲击荷载下,RC梁可能会出现多种破坏模式,正确评估冲击荷载下构件的变形与破坏模式是构件抗冲击设计的关键。刘廷权等[8]采用分别考虑弯曲与剪切响应的单自由度系统,从结构失效概率角度研究冲击荷载下RC梁的动力特性, 通过计算初步判别RC梁在冲击荷载下的破坏模式。师燕超等[70]提出RC梁抗爆分析的改进等效单自由度方法,基于位移评估爆炸荷载下RC梁的破坏模式。唐泓等[71]利用临界剪切理论,探索判断RC梁冲剪破坏的分析方法。对于冲击荷载下RC梁破坏模式的判别,本文中基于前期研究,提出基于承载力的判别准则。该判别准则包括2个方面:1)计算RC梁承受的动弯矩M与动剪力V;2)计算动载下RC梁的弯曲极限承载力Mu与剪切极限承载力Vu,考虑材料的应变率效应,在极限承载力的计算中引入动力增大因子。然后将受力与极限承载力的比值作为RC梁破坏模式判别的依据:γM=M/Mu,γM大于1时RC梁发生弯曲破坏,否则不发生弯曲破坏;γV=V/Vu, γV大于1时RC梁发生剪切破坏,否则不发生剪切破坏。
相对于弯曲与剪切破坏,弯剪破坏模式存在2种不同破坏特征的耦合作用,难以从破坏機制方面解释RC梁弯剪破坏的发生条件。图6所示为冲击荷载下RC梁的破坏模式判别准则示意图。准则界定0.75γM-0.50γV曲线相互作用区为弯剪破坏区,破坏模式判别准则示意图可以划分为剪切破坏区、弯剪破坏区和弯曲破坏区。破坏点的位置决定了RC梁的破坏模式,曲线1预测RC梁发生弯曲破坏,曲线2预测RC梁发生弯剪破坏,曲线3预测RC梁发生剪切破坏。
5 冲击荷载下RC梁抗冲击评估方法
RC梁的抗冲击设计方法大致分为2类:1)基于弹塑性理论的极限分析方法,采用理论分析或数值方法计算冲击荷载下RC梁的响应;2)基于试验数据统计的经验方法。
Feldman等[72]最早提出的等效单自由度(SDOF)方法用于分析计算冲击荷载下梁的弯曲响应。SDOF方法计算简便,可以给出工程设计中所需的梁挠度及支座反力,但是进行冲击响应计算时,SDOF方法需要获知冲击力时程曲线,而该曲线无法直接预判或获取,需要对其进行估计。该工作较复杂,尚没有被广泛接受的模型,并且冲击荷载下的结构响应复杂,SDOF方法假定的简单挠曲线方程可能存在与实际变形不符的情况,影响响应计算的精度和适用范围。
针对SDOF方法存在的冲击力时程曲线获取较难的问题,Fujikake等[23]假定冲击过程中动量守恒,采用如图7[23]所示的双自由度弹簧阻尼器系统避免了该问题。该方法可以直接计算冲击过程中的能量损耗,得到估算RC梁在冲击荷载下的最大挠度δmax公式,即
m2v2c2-Er+(m1+m2)gδmax=∫δmax0P(δ)dδ ,(14)
式中:m1为梁的等效单自由度质量;m2为落锤质量;g为重力加速度;δ为跨中挠度;P(δ)为RC梁刚度的荷载-位移关系;Er为能量损耗,满足
Er=m1m22(m1+m2)v2c 。(15)
在RC梁仅出现整体弯曲破坏时,式(14)与试验跨中挠度吻合良好,但是该方法只能获得梁的跨中挠度,对于实际设计给出的信息较少。
Krauthammer等[73]定义了一个多段剪切抗力函数模型,将单自由度体系推广到考虑RC梁剪切破坏响应的阶段。Yi等[74]利用双质点系统,将冲击过程分为局部响应和整体响应2个阶段,基于修正压力场理论的动态破坏准则,提出了能够评估RC梁动态力矩和剪切需求的模型。王明洋等[75]以弯曲理论为基础,建立梁在准弹性阶段和塑性阶段的简化模型,提出了RC梁低速冲击响应的计算方法。除了等效简化模型,Bernoulli-Euler梁理论和经典Timoshenko梁理论也常用于计算RC梁在冲击荷载下的动力响应[76-77]。
随着计算机技术和计算力学的迅速发展,冲击过程高精度数值模拟成为可能,因此许多评估方法基于数值仿真展开。Cotsovos[78]利用ANSYS软件数值模拟研究发现,高速率加载时应力波传播效应导致RC梁有效长度减小,通过将RC梁有效长度梁段等效为承受静载的梁,使用静力设计公式计算RC梁的抗弯和抗剪承载能力。周泽平等[79]采用离散体模型模拟冲击体与梁整体和局部的相互作用,推导了RC梁在不同阶段的变形刚度和弹塑性阶段的运动方程。孟一[80]在优化混凝土本构关系的基础上,使用非线性有限元软件LS-DYNA完成两端铰支RC梁的数值模拟分析,通过大量数值计算,提出了RC梁在冲击下的简化计算方法。需要说明的是,数值模拟结果能否反映梁的实际性能仍值得商榷,研究者需要进一步研究能准确反映冲击荷载下结构材料真实特性的本构关系。
在RC梁的抗冲击设计方法中,因构件的大变形而导致冲击能量耗散被认为是一种较合理的计算方法,公式为
δ=αEkd/Fusd ,(16)
式中:Ekd为输入能量;Fusd为静力承载力;α为拟合系数。
Kishi等[62]通过分析冲击试验数据,假设冲击下RC梁最大支座反力Rud为静弯曲承载力Pusd的2倍,吸收能量Ea为输入能量Ekd的70%,得到经验公式
δrd=0.35Ekd/Pusd
,(17)
式中δrd为残余挠度。Kishi等[57]基于试验结果提出无腹筋梁在冲击荷载下的抗剪计算公式,即
δrd=0.8Ekd/Vusd ,(18)
式中Vusd为静剪切承载力。Tachibana等[81]给出估算冲击荷载下RC梁跨中最大挠度的经验公式为
δmax=0.552Ekd/Pusd 。(19)
在经验公式(17)、(19)中,梁的静弯曲承载力可以通过冲击能量与冲击中需要控制的跨中挠度进行确定。Kishi等[82]未改变抗冲击经验公式的形式,在试验基础上拟合得到系数α=0.63。在冲击能量与跨中挠度相同时,通过系数0.63计算得到的静弯曲承载力为Tachibana等[81]提出公式计算值的1.2倍,因此采用系数0.63相对安全。
Kishi等[82]提出的考虑能量与变形的经验公式虽然合理,但是过于简化,没有考虑冲击质量、速度等重要参数对冲击性能的影响。赵德博等[83]通过对已有试验数据进行对比发现,在利用式(19)计算所得承载力和能量相同的条件下,RC梁的变形随冲击质量的增大而增大,因此采用固定的系数α并不妥当。赵德博等[83]利用双质点模型,将落锤冲击RC梁的过程简化为撞击过程,改进了估算冲击过程中梁体最大挠度的经验公式,即
δmax=Ekd/Pusda2/(a0+a1b) ,(20)
式中:a0=0.838 4;a1=-0.021 73;a2=0.825 9;b=m2/m1。 虽然式(20)考虑了冲击质量的影响,准确度也大幅提高,但是仍然是基于试验结果统计得到的,并且没有取得一致认识,还不足以达到精确结构设计的需求,相关研究仍然需要继续深入开展。
6 结论
本文中对冲击荷载、材料的应变率效应、RC梁的動态响应与破坏模式、设计评估方法等进行综述,分析RC梁抗冲击性能的相关研究进展,得到以下主要结论:
1)冲击荷载下RC梁性能的影响因素复杂,主要有冲击速度、梁的刚度及抗弯与抗剪强度,已有研究较明确地给出了这些因素的影响规律,为进一步深入分析与设计RC梁抗冲击性能奠定了基础。
2)冲击荷载下RC梁的破坏过程与破坏模式已基本掌握,但是对破坏机制与破坏模式判别准则的研究有所欠缺。
3)关于冲击荷载下RC梁的抗冲击评估方法虽然较多,但是差异较大,考虑因素不全,仍然需要在充分的试验数据和精确模型分析结果基础上进行进一步研究。
参考文献:
[1]CHEN Y, MAY I M. Reinforced concrete members under drop-weight impacts[J]. Structures and Buildings, 2009, 162(1): 45.
[2]付应乾, 董新龙. 落锤冲击下钢筋混凝土梁响应及破坏的实验研究[J]. 中国科学:技术科学, 2016, 46(4): 400.
[3]姜华, 贺拴海, 王君杰. 钢筋混凝土梁冲击试验数值模拟研究[J]. 振动与冲击, 2012, 31(15): 140.
[4]刘飞, 罗旗帜, 蒋志刚. 低速冲击下RC梁的动态响应和破坏机理研究[J]. 工程力学, 2015, 32(5): 155.
[5]赵武超, 钱江, 张文娜. 冲击荷载下钢筋混凝土梁的性能及损伤评估[J]. 爆炸与冲击, 2019, 39(1): 015102.
[6]曾翔, 许斌. 无腹筋钢筋混凝土梁抗冲击行为试验研究[J]. 土木工程学报, 2012, 45(9): 65.
[7]窦国钦, 杜修力, 李亮. 冲击荷载作用下钢纤维混凝土配筋梁性能试验[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(10): 864.
[8]刘廷权, 王兴国, 葛楠. 钢筋混凝土柱在侧向撞击作用下破坏模式研究[J]. 武汉理工大学学报, 2010, 32(9): 188.
[9]李宏男, 张宇, 刘跃伟, 等. 钢筋混凝土构件动力加载试验数据库[J]. 建筑结构学报, 2016, 37(9): 78.
[10]MALVAR L J, ROSS C A. Review of strain rate effects for concrete in tension[J]. ACI Materials Journal, 1998, 95(6): 735.
[11]MALVAR L J. Review of static and dynamic properties of steel reinforcing bars[J]. ACI Materials Journal, 1998, 95(5): 609.
[12]李敏, 李宏男. 建筑钢筋动态试验及本构模型[J]. 土木工程学报, 2010, 43(4): 70.
[13]BENTUR A, MINDESS S, BANTHIA N P. The behaviour of concrete under impact loading: experimental procedures and method of analysis[J]. Materials and Structures, 1986, 19(5): 371.
[14]SOLEIMANI S M, BANTHIA N, MINDESS S. Behavior of RC beams under impact loading: some new findings[C]//Proceedings of the 6th International Conference on Fracture Mechanics of Concrete and Concrete Structures, June 17-22, 2007, Catania, Italy. London: Taylor and Francis, 2007: 867.
[15]COTSOVOS D M, STATHOPOULOS N D, ZERIS C A. Beha-vior of RC beams subjected to high rates of concentrated loading[J]. Journal of Structural Engineering, 2008, 134(12): 1839.
[16]DANCYGIER A N, YANKELEVSKY D Z, JAEGERMANN C. Response of high performance concrete plates to impact of non-deforming projectiles[J]. International Journal of Impact Engineering, 2007, 34(11): 1768.
[17]LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile[J]. International Journal of Impact Engineering, 2003, 28(1): 93.
[18]ZHANG M H, SHIM V P W, LU G, et al. Resistance of high-strength concrete to projectile impact[J]. International Journal of Impact Engineering, 2005, 31(7): 825.
[19]KRAUTHAMMER T. Blast mitigation technologies: developments and numerical considerations for behavior assessment and design[C]//Proceedings of International Conference on Structure under Shock and Impact, June 24-26, 1998, Thessaloniki, Greece. Southampton: WIT Press, 1998: 3.
[20]FUJIKAKE K, SENGA T, UEDA N, et al. Study on impact response of reactive powder concrete beam and its analytical model[J]. Journal of Advanced Concrete Technology, 2006, 4(1): 99.
[21]BIGGS J M. Introduction to structural dynamics[M]. New York: McGraw-Hill, 1964.
[22]宋敏. 沖击加载下钢筋混凝土梁的结构响应与数值模拟[D]. 太原: 太原理工大学, 2018: 19.
[23]FUJIKAKE K, LI B, SOEUN S. Impact response of reinforced concrete beam and its analytical evaluation[J]. Journal of Structural Engineering, 2009, 135(8): 939-947.
[24]赵德博. 冲击荷载作用下钢筋混凝土梁响应特征及设计方法研究[D]. 长沙: 湖南大学, 2017: 76-81.
[25]CEB-FIP. FIB model code for concrete structures 2010[S]. Lausanne Switzerland: Thomas Thetford, 2010.
[26]BSI. Eurocode 1: actions on structures: parts 1-6: general action: action during execution: EN 1991-1-6: 2005[S]. London: British Standards Institution, 2005.
[27]孙训方, 方孝淑, 关来泰. 材料力学: Ⅱ[M]. 北京: 高等教育出版社, 2009.
[28]ABRATE S. Modeling of impacts on composite structures[J]. Composite Structures, 2001, 51(2): 130.
[29]PHAM T M, HAO H. Prediction of the impact force on reinforced concrete beams from a drop weight[J]. Advances in Structural Engineering, 2016, 19(11): 1713.
[30]ABRATE S. Impact on composite structures[M]. Cambridge: Cambridge University Press, 2005: 75.
[31]孙建运, 李国强. 动力荷载作用下固体材料本构模型研究的进展[J]. 四川建筑科学研究, 2006, 32(5): 144-145.
[32]BINDIGANAVILE V S. Dynamic fracture toughness of fiber-reinforced concrete[D]. Canada: The University of British Columbia, 2003: 9.
[33]TAKEDAJ,TACHIKAWAH.Themechanicalpropertiesofseveralkinds of concrete at compressive, tensile, and flexural tests in high rates of loading[J]. Transactions of the Architectural Institute of Japan, 1962, 77: 1-6.
[34]HUGHES B P, GREGORY R. Concrete subjected to high rates of loading in compression[J]. Magazine of Concrete Research, 1972, 24(78): 25-36.
[35]ROSS C A, TEDESCO J W, KUENNEN S T. Effects of strain-rate on concrete strength[J]. ACI Material Journal, 1995, 92(1): 37-47.
[36]ADHIKARY S D, BING L, FUJIKAKE K. Dynamic behavior of reinforced concrete beams under varying rates of concentrated loading[J]. International Journal of Impact Engineering, 2012, 47: 29.
[37]JOHNSONGR,COOKWH.Aconstitutive model and data for metals subjected to large strains high strain rates and high temperatures[C]//Proceeding of the 7th International Symposium on Ballistics, September 21-23, 1983, Hague, Netherlands. Hague: International Ballistics Society, 1983: 543.
[38]COWPER G R, SYMONDS P S. Strain hardening and strain rate effects in the impact loading of cantilever beams[R]. Providence: Brown University, 1958: 5-8.
[39]CEB. CEB-FIP model code 1990[S]. Wiltshire, UK: Redwood Books, 1993: 49-50.
[40]MALVAR L J, CRAWFORD J E. Dynamic increase factors for concrete[C]//Proceedings of the 28th DDESB Seminar, August 15-17, 1998, Orlando, USA. Orlando: ANSI, 1998: 8.
[41]HAO Y F, HAO H. Influence of the concrete DIF model on the numerical predictions of RC wall responses to blast loadings[J]. Engineering Structures, 2014, 73(15): 26.
[42]OHNUMA H, ITO C, NOMACHI S G. Dynamic response and local rupture of reinforced concrete beam and slab under impact loading[C]//Transactions of the 8th International Conference on Structural Mechanics in Reactor Technology, July 22-24, 1985, Amsterdam, Brussels. Belgium: North-Holland Physics Publishing, 1985: 179.
[43]許斌, 曾翔. 冲击荷载作用下钢筋混凝土梁性能试验研究[J]. 土木工程学报, 2014, 47(2): 41.
[44]窦国钦, 杜修力, 李亮. 冲击荷载作用下高强钢筋混凝土梁性能试验[J]. 天津大学学报(自然科学与工程技术版), 2014, 47(12): 1072.
[45]耿佳. 冲击荷载作用下钢筋混凝土梁的尺寸效应研究[D]. 济南: 济南大学, 2020.
[46]方秦, 吴平安. 爆炸荷载作用下影响RC梁破坏形态的主要因素分析[J]. 计算力学学报, 2003, 20(1): 39.
[47]梅福林, 董新龙, 俞鑫炉. 不同落锤速度冲击下混凝土和RC梁破坏研究[J]. 宁波大学学报(理工版), 2017,30(5): 86.
[48]霍静思, 胡开赢. RC梁冲击破坏机理试验研究与残余变形预测方法探讨[J]. 湖南大学学报(自然科学版), 2017, 44(1): 114.
[49]TRAVAS V, OZBOLT J, KOZAR I. Failure of plain concrete beam at impact load: 3D finite element analysis[J]. International Journal of Fracture, 2009, 160(1): 40.
[50]OZBOLT J, SHARMA A. Numerical simulation of reinforced concrete beams with different shear reinforcements under dynamic impact loads[J]. International Journal of Impact Engineering, 2011, 38(12): 949.
[51]MYLREA T D. Effect of impact on reinforced concrete beams[J]. Highway Research Board Proceedings, 1940, 36(6): 137.
[52]李猛深, 李杰, 李宏, 等. 爆炸荷载下钢筋混凝土梁的变形和破坏[J]. 爆炸与冲击, 2015, 35(2): 179.
[53]LAN C, SHAH S P. Effect of loading rate on anchorage bond and beam-column joints[J]. ACI Structural Journal, 1989, 86(2): 141.
[54]FU H C, ERKI M A, SECKIN M. Review of effects of loading rate on reinforced concrete[J]. Journal of Structural Engineering, 1991, 117(12): 3678.
[55]王子琪, 柳锦春. 爆炸荷载作用下钢筋混凝土梁变形指标限值研究[J]. 防护工程, 2018, 40(3): 26.
[56]MA G W, SHI H J, SHU D W. P-I diagram method for combined failure modes of rigid-plastic beams[J]. International Journal of Impact Engineering, 2007, 34(6): 1085.
[57]KISHI N, MIKAMI H, MATSUOKA K G, et al. Impact behavior of shear-failure-type RC beams without shear rebar[J]. Inter-national Journal of Impact Engineering, 2002, 27(9): 958-959, 966.
[58]趙武超, 钱江. 冲击荷载下钢筋混凝土梁局部响应特征研究[J]. 湖南大学学报(自然科学版), 2019, 46(3): 31.
[59]ROSSI P. Dynamic behavior of concretes: from the material to the structure[J]. Materials and Structures, 1994, 27(6): 322.
[60]岸徳光, 三上浩, 松岡健一, など. 静載荷時に曲げ破壊が卓越するRC梁の耐衝撃設計法に関する一提案[C]//土木学会. 土木学会論文集: 647. 東京: 土木学会, 2000: 189.
[61]SOLEIMANI S M. Sprayed glass fiber reinforced polymers in shear strengthening and enhancement of impact resistance of reinforced concrete beams[D]. Vancouver: The University of British Columbia, 2006.
[62]KISHI N, NAKANO O, MATSUOKA K G, et al. Experimental study on ultimate strength of flexural-failure-type RC beams under impact loading[C]//Transactions of the 16th International Concrete on Structural Mechanics in Reactor Technology. August 12-17, 2001, Washington, USA. Washington D C: IASMiRT, 2001: 3, 7.
[63]SAATCI S, VECCHIO F J. Effects of shear mechanisms on impact behavior of reinforced concrete beams[J]. ACI Structural Journal, 2009, 106(1): 82.
[64]KISHI N, BHATTI A Q. An equivalent fracture energy concept for nonlinear dynamic response analysis of prototype RC girders subjected to falling-weight impact loading[J]. International Journal of Impact Engineering, 2010, 37(1): 104-105.
[65]KRAUTHAMMER T, SHAHRIAR S, SHANAA H M. Response of reinforced concrete elements to severe impulsive loads[J]. Journal of Structural Engineering, 1990, 116(4): 1072.
[66]阎石, 张亮, 王丹. 钢筋混凝土板在爆炸荷载作用下的破坏模式分析[J]. 沈阳建筑大学学报(自然科学版), 2005, 21(3): 177.
[67]师燕超, 李忠献. 爆炸荷载作用下钢筋混凝土柱的动力响应与破坏模式[J]. 建筑结构学报, 2008, 29(4): 112.
[68]SAATCI S. Behaviour and modelling of reinforced concrete structures subjected to impact loads[D]. Canada: University of Toronto, 2007: 203, 285.
[69]曾翔. 冲击和快速加载作用下钢筋混凝土梁柱构件性能试验与数值模拟研究[D]. 长沙: 湖南大学, 2014: 135.
[70]师燕超, 张浩, 李忠献. 钢筋混凝土梁式构件抗爆分析的改进等效单自由度方法[J]. 建筑结构学报, 2019, 40(10): 8.
[71]唐泓, 苏健军, 翟红波, 等. 近场爆炸作用下简支钢筋混凝土梁冲剪破坏的预测方法[J]. 兵器装备工程学报, 2022, 43(2): 117.
[72]FELDMAN A, SIESS C P. Investigation of resistance and behavior of reinforced concrete members subjected to dynamic loading: part Ⅱ[R]. Illinois: University of Illinois at Urbana-Champaign, 1958.
[73]KRAUTHAMMER T, BAZEOS N, HOLMQUIST T J. Modified SDOF analysis of RC box-type structures[J]. Journal of Structural Engineering, 1986, 112(4): 726.
[74]YI W J, ZHAO D B, KUNNATH S K. Simplified approach for assessing shear resistance of reinforced concrete beams under impact loads[J]. ACI Structural Journal, 2016, 113(4): 747.
[75]王明洋, 王德榮, 宋春明. 钢筋混凝土梁在低速冲击下的计算方法[J]. 兵工学报, 2006, 27(3): 399.
[76]MAGNUSSON J, HALLGREN M, ANSELL A. Shear in concrete structures subjected to dynamic loads[J]. Structural Concrete, 2014, 15(1): 55.
[77]方秦, 郭东, 张亚栋, 等. 梁的剪力动力系数的确定[J]. 工程力学, 2005, 22(5): 181.
[78]COTSOVOS D M. A simplified approach for assessing the load-carrying capacity of reinforced concrete beams under concentrated load applied at high rates[J]. International Journal of Impact Engineering, 2010, 37(8): 907.
[79]周泽平, 王明洋, 冯淑芳, 等. 钢筋混凝土梁在低速冲击下的变形与破坏研究[J]. 振动与冲击, 2007, 26(5): 99.
[80]孟一. 冲击荷载作用下钢筋混凝土梁的试验及数值模拟研究[D]. 长沙: 湖南大学, 2012.
[81]TACHIBANA S, MASUYA H, NAKAMURA S. Performance based design of reinforced concrete beams under impact[J]. Natural Hazards and Earth System Sciences, 2010, 10(6): 1075.
[82]KISHI N, MIKAMI H. Empirical formulas for designing reinforced concrete beams under impact loading[J]. ACI Structural Journal, 2012, 109(4): 517.
[83]赵德博, 易伟建. 钢筋混凝土梁抗冲击性能和设计方法研究[J]. 振动与冲击, 2015, 34(11): 144.
(责任编辑:王 耘)
