基于传递矩阵法的足式机器人四连杆腿部机构正向与逆向动力学分析
2024-01-12赵鑫宇宋延松朱晓蕙刚宪约柴汇
赵鑫宇 宋延松 朱晓蕙 刚宪约 柴汇


文章编号:1671-3559(2024)01-0115-08DOI:10.13349/j.cnki.jdxbn.20231223.001
摘要:为了保证足式机器人腿部机构的控制准确性与实时性,利用向量代数方法,对足式机器人四连杆腿部机构进行几何运动学分析;根据有限元形函数理论,建立足式机器人四连杆腿部机构典型构件的质量离散方法;在几何运动学分析的基础上,基于力矩平衡原理,分别进行正向与逆向动力学分析;利用线性变换原理并结合传递矩阵法,建立足式机器人四连杆腿部机构正-逆向动力学统一模型,并利用Adams软件建立足式机器人四连杆腿部机构虚拟样机模型,进行正向与逆向动力学仿真实例分析。结果表明,所建立的足式机器人四连杆腿部机构正-逆向动力学统一模型与虚拟样机模型3个油缸力与3个方向足底力的误差分别小于1%与3%,验证了所建立的足式机器人四连杆腿部机构正-逆向动力学统一模型能够精确地求解油缸力与足底力。
关键词:足式机器人;腿部机构;动力学分析;传递矩阵法
中图分类号:TP242.3
文献标志码:A
开放科学识别码(OSID码):
Forward and Reverse Dynamics Analyses on Four-bar Linkage
Leg Mechanism of Legged Robots Based on Transfer Matrix Method
ZHAO Xinyu1, SONG Yansong1, ZHU Xiaohui1, GANG Xianyue1, CHAI Hui2
(1. School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255000, Shandong, China;
2. Center for Robotics, Shandong University, Jinan 250061, Shandong, China)
Abstract: To ensure control accuracy and instantaneity of leg mechanism for legged robots, geometric kinematic analysis on four-bar linkage leg mechanism of legged robots was carried out by using vector algebra method. A mass dispersion method for typical bars of four-bar linkage leg mechanism of legged robots was established according to finite element form function theory. On the basis of geometric kinematic analysis and principle of moment balance, forward and reverse dynamic analyses were carried out respectively. A unified forward-reverse dynamics model for four-bar linkage leg mechanism of legged robots was established by using principle of linear transformation and combining transfer matrix method. A virtual prototype model for four-bar linkage leg mechanism of legged robots was established by using Adams software for example analysis of forward and reverse dynamics simulation. The results show that errors of three cylinder forces and plantar forces in three directional between the established unified forward-reverse dynamics model and the virtual prototype model for four-bar linkage leg mechanism of legged robots are less than 1% and 3% , which verifies that the established unified forward-reverse dynamics model for four-bar linkage leg mechanism of legged robots can accurately solve cylinder force and plantar force.
Keywords: legged robot; leg mechanism; dynamics analysis; transfer matrix method
收稿日期:2022-09-25 網络首发时间:2023-12-25T10:35:24
基金项目:国家自然科学基金项目(62073191);山东省重大科技创新工程项目(2019JZZY020317);山东省自然科学基金项目(ZR2020ME140)
第一作者简介:赵鑫宇(1998—), 男, 山东淄博人。 硕士研究生, 研究方向为动力学分析仿真、结构优化。E-mail: zhaoxinyu7419@163.com。
通信作者简介:刚宪约(1977—),男,山东济南人。教授,博士,硕士生导师,研究方向为结构优化、车辆系统动力学。E-mail: gangxianyue@
sdut.edu.cn。
网络首发地址:https://link.cnki.net/urlid/37.1378.N.20231223.1236.002
足式机器人着地点是离散的,可以在地面上选择最优位置,并且能够跨越障碍,几乎可以适应各种复杂地形,因此在制造业、服务业、军事、航天、核工业等领域具有非常广阔的应用前景[1]。机器人动力学主要研究机器人末端位置所受载荷与各关节所需驱动力之间的关系,动力学分析可以准确地判断机器人在工作时腿部机构的受力,为后期优化和高效稳定控制奠定基础。
为了对机器人进行实时控制与结构设计, 改善运动性能, 许多学者利用不同方法对机器人进行动力学建模。 崔敏其[2]利用拉格朗日公式对SCARA型机器人的动力学模型进行了详细推导;刘芳华等[3]利用虚功原理对机器人进行动力学建模, 研究关节驱动力矩与结构尺寸、位置等之间的关系;张铁等[4]基于牛顿-欧拉方法对机器人建立动力学方程, 得出机器人运动时的关节力矩, 为动力学控制提供了基础计算公式;Wu等[5]利用拉格朗日公式和能量法建立動力学模型, 并利用Adams软件仿真验证动力学模型的准确性。 正向动力学分析是指以腿部机构各油缸的力和位移为输入, 预测足端输出的力和位移;逆向动力学分析是指依据期望得到的足端输出力和位移, 反求各油缸应施加的输入力和位移。
已有研究中正向与逆向动力学分析需要2种完全不同的数学方程,计算过程复杂,影响控制的准确性和实时性。本文中基于力矩平衡原理,对四连杆腿部机构进行正向与逆向动力学分析,利用线性变换原理并结合传递矩阵法,将正向与逆向动力学分析合二为一,建立足式机器人四连杆腿部机构(简称腿部机构)正-逆向动力学统一模型。
1 腿部机构几何运动学分析
对足式机器人的腿部机构进行几何运动学分析,研究腿部机构在运动过程中几何参数与运动参数之间的关系,为动力学分析提供理论支持[6]。
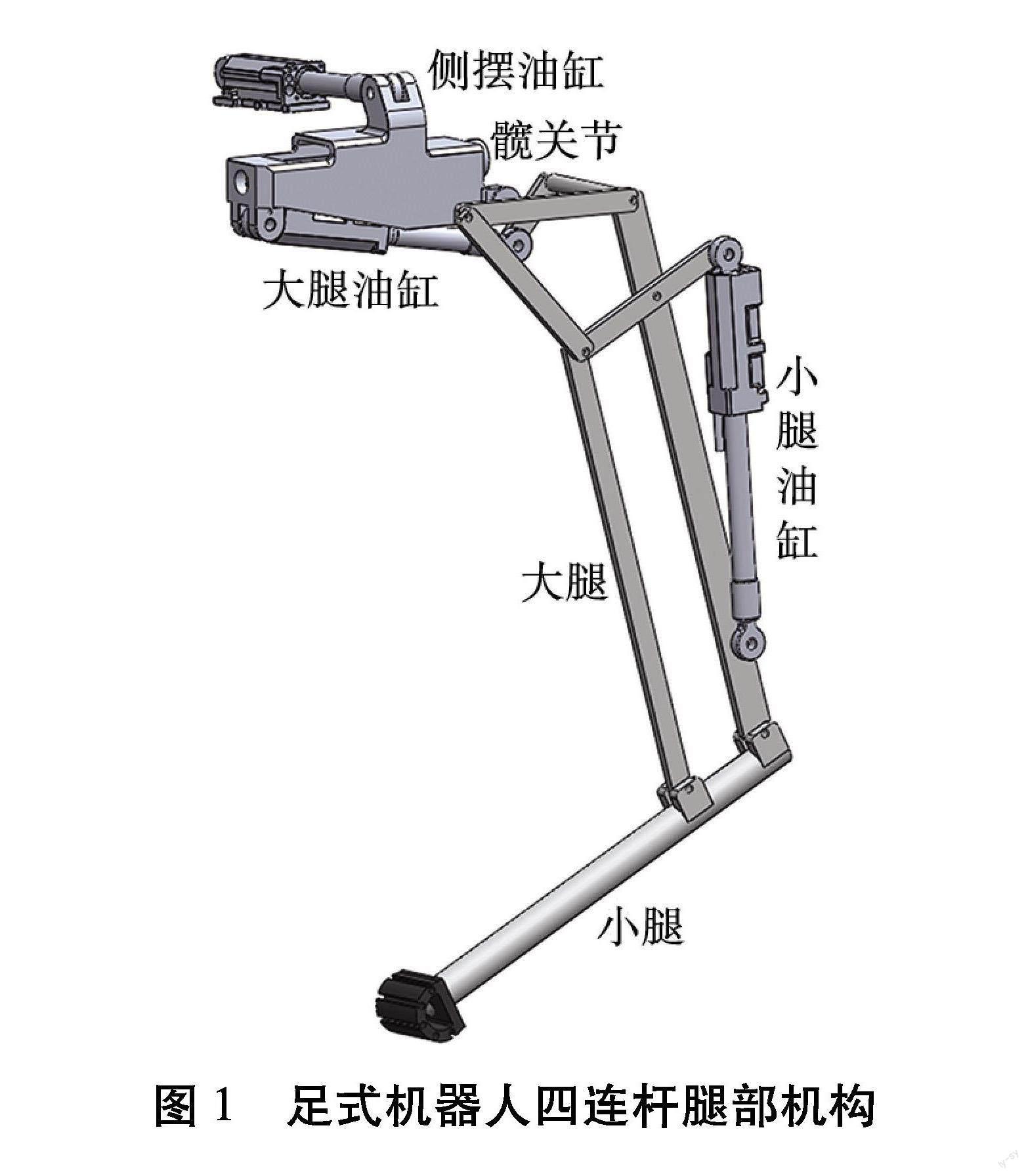
足式机器人的腿部机构包括侧摆油缸、髋关节、大腿与小腿, 如图1所示。 侧摆油缸控制腿部机构绕髋关节侧向摆动, 左端与机架铰接, 右端与髋关节铰接, 髋关节铰接在机架上。 大腿和小腿也分别由2个油缸通过连杆机构实现在腿部机构平面内的纵向摆动。 由于腿部髋关节的侧摆和腿部机构的纵摆的控制相互独立, 因此可将几何运动学分析分2步进行:首先在腿部纵摆平面内进行几何运动学分析,只考虑在腿部机构的纵向摆动自由度, 根据机构杆件长度、油缸工作行程和关节转角计算腿部机构各关节点在腿部随体坐标系的位置姿态[7];然后在腿部侧摆平面内根据髋关节侧摆角度利用坐标变换, 计算整个腿部机构铰接点在全局坐标系中的位置。
1.1 腿部机构坐标系建立
对足式机器人整机和腿部机构分别建立坐标系,如图2所示。
整机全局坐标系XgloYgloZglo以髋关节侧向摆动支点O为坐标原点,竖直向上为Zglo轴正方向,水平向右为Yglo轴正方向, Xglo轴满足右手螺旋定则。其中,大腿与小腿所在的平面为腿部机构纵向摆动平面,垂直于纸面的投影为BK,O1N为侧摆油缸,控制整个腿部机构绕Xglo轴进行侧摆运动。由于腿部机构平面存在绕髋关节侧向摆动支点O的侧向摆动,因此腿部随体坐标系会绕Xglo轴旋转。
腿部随体坐标系XlegYlegZleg以腿部纵向摆动支点B为坐标原点,Xleg轴水平向右为正方向,Yleg轴垂直于腿部平面向外为正方向,Zleg轴竖直向上为正方向。其中杆件BI为大腿,杆件IK为小腿,AC为大腿油缸,推动大腿实现绕Yleg轴的纵向摆动;QH为小腿油缸,控制小腿进行纵向摆动。
1.2 纵向摆动平面几何运动学分析
首先对腿部纵向摆动平面进行几何运动学分析,计算腿部机构各关节铰接点及连杆质心在腿部随体坐标系中的位置。在图2(b)中,A、B点分别固定在机架上,已知A、B点坐标,机构杆件长度、油缸长度及关节角计算其他铰接点位置以及足端K的坐标。
R点坐标可由腿部随体坐标系中B点位置、杆件BR长度lBR和关节转角θ1求得,即
RXleg
RYleg
RZleg=BXleg
BYleg
BZleg+lBRcos θ1
0
sin θ1 ,(1)
式中(RXleg, RYleg, RZleg
)、(BXleg, BYleg, BZleg)分别为腿部随体坐标系XlegYlegZleg中R、B点的坐标。
同理,可分别求得H、I点在腿部随体坐标系中的坐标。
根据I点坐标、杆件IJK各段长度以及转角θ2可求得J点坐标,即
JXleg
JYleg
JZleg=IXleg
IYleg
IZleg+lIJcos θ2
0
sin θ2 ,(2)
式中:(JXleg, JYleg, JZleg)、(
IXleg, IYleg, IZleg)为腿部随体坐标系中J、I点坐标;lIJ为杆件IJ长度。
K点求解方法同理。利用余弦定理,根据点A、B坐标与杆件AC、BC的长度lAC、lBC,计算C点腿部随体坐标系中的坐标(CXleg, CYleg, CZleg)。
同理,根据R、H点坐标,以及油缸QH、杆件RQ的长度,计算Q点腿部随体坐标系中的坐标(QXleg, QYleg, QZleg)。
由DB逆时针转动到CB的转角φ2, lBC, 杆件BD长度lBD,以及B、C点坐标,可求得由B点指向C点的单位向量
(nBC,Xleg, nBC,Yleg, nBC,Zleg),最终可得D点坐标为
DXlegDYlegDZleg=
BXlegBYlegBZleg
+lBD
cosφ2sinφ200-sinφ2cosφ2
nBC,Xleg0nBC,Zleg。(3)
由R、Q点坐标以及杆件ER长度lER、向量RQ的单位向量(nRQ,Xleg, nRQ,Yleg, nRQ,Zleg),可得E点坐标为
EXlegEYlegEZleg=
RXlegRYlegRZleg
-lER
nRQ,XlegnRQ,YlegnRQ,Zleg 。(4)
杆件质心位置需要利用杆件局部坐标系计算。以杆件AB为例,建立杆件局部坐标系XlocYlocZloc,选择铰接点A为杆件局部坐标系的原点,Xloc轴正方向沿着杆件指向另一个铰接点B,逆时针旋转90°为Yloc轴正方向,根据右手螺旋定则确定Zloc轴正方向,如图3所示。
两节点线性杆件AB的局部坐标系
根据各杆件质心在杆件局部坐标系中的位置,通过坐标变换求出杆件质心Cm在腿部随体坐标系中的坐标为
Cm,Xleg
Cm,Yleg
Cm,Zleg=
AXleg
AYleg
AZleg+
nAB,Xleg-nAB,Zleg
00
nAB,ZlegnAB,Xleg
Cm,Xloc
Cm,Yloc
Cm,Zloc,(5)
其中nAB,Xleg
nAB,Yleg
nAB,Zleg=1lAB
BXleg-AXleg
BYleg-AYleg
BZleg-AZleg ,(6)
式中:(Cm,Xloc, Cm,Yloc, Cm,Zloc)
为杆件质心Cm在杆件局部坐标系中的坐标;(nAB,Xleg, nAB,Yleg, nAB,Zleg)为杆件AB在腿部随体坐标系中的单位矢量;lAB为杆件AB长度;(AXleg, AYleg, AZleg)为铰接点A在腿部随体坐标系中的坐标。
1.3 侧向摆动坐标变换
由于腿部机构纵摆平面在侧摆油缸的作用下绕髋关节进行侧向摆动,则各点的全局坐标可利用坐标转换公式和侧摆角θ3计算。
以K点在全局坐标系中的位置为例,即
KXglo
KYgloKZglo=
OXgloOYglo
OZglo+
10
0cosθ3-sinθ3
0sinθ3cosθ3
KXleg
KYleg
KZleg,(7)
式中:(OXglo, OZglo, OZglo)为侧摆支点O在全局坐标系中的坐标;(KXleg, KYleg, KZleg)为K點在腿部随体坐标系中的坐标。
2 杆件质量离散方法
在进行力学分析时,腿部机构的自身重力是不可忽略的重要参数[8]。为了更方便地求解各关节的受力情况,利用有限元方法,将腿部机构各杆件的质量近似离散到相关铰接点[9]。
足式机器人腿部机构杆件主要有两节点线性杆件、三节点三角形杆件和多节点线性杆件3种形式。3种杆件的质量离散方法分别为线性插值法、面积坐标插值法、等质量矩分配法。
2.1 两节点线性杆件
将图3所示的杆件AB视作两节点线性有限单元,杆件质量离散到铰接点A的质量为
mA=mABlBCmlAB ,(8)
式中:mAB为杆件AB的质量;lBCm为B点与杆件质心Cm的距离。
杆件质量离散到铰接点B的质量为
mB=mABlACmlAB ,(9)
式中lACm为A点与杆件质心Cm的距离。
2.2 三节点三角形杆件
借鉴有限元分析中三节点三角形单元的位移场表达方式即形函数理论[10],对三节点三角形杆件进行质量离散。以三节点三角形杆件BCD为例,如图4所示,利用杆件铰接点坐标,采用面积坐标插值法,将质量离散到3个铰接点上。同理,此方法适用于三节点三角形杆件ERQ、IJK。
将三节点三角形杆件质量等效为在质心处的集中质量,进而离散成在节点上的质量,则节点B、C、D的等效节点质量为
mBmCmD=mBCDNBNCND ,(10)
其中NC=12S(aC+bCCXleg+cCCYleg) ,
aC=DXlegDYleg
BXlegBYleg=DXlegBYleg-BXlegDYleg ,
bC=-1DYleg
1BYleg=DYleg-BYleg ,
cC=1DXleg
1BXleg=BXleg-DXleg ,
(11)
式中:mBCD为三节点三角形杆件BCD的质量;S为BCD的面积。
类似地,将式(11)中B、C、D下标轮换,如将下标C与D以及C与D的坐标互换后进行计算,即可求得NB、ND。
将式(11)计算得出的(NB, NC, ND)代入式(10),即可得到三节点三角形杆件质量离散到3个铰接点的等效质量。
2.3 多节点线性杆件
图5所示为腿部机构的多节点线性杆件结构。例如BRHI杆件,可采用等质量矩分配法。
由力矩平衡原理可知, 杆件左、右两侧铰接点对质心Cm的总质量矩相等,假设单侧质量与距离成反比,求解线性方程组可以得到左、右侧总质量矩Mleft、Mright,即
∑1∑1bj
nleft-nright
Mleft
Mright=m0,(12)
式中:aj(i=1,2)、bj(j=1,2,3)分别为左、右侧各铰接点到质心Cm的距离;nleft、nright分别为质心的左、右侧节点个数;m为杆件质量。
左侧各节点的等效质量为
mi=Mleftai ,(13)
右侧各节点的等效质量为
mj=Mrightbj 。(14)
3 腿部机构正向与逆向动力学分析
由于足式机器人腿部运动过程中结构件加速度远小于重力加速度,产生的惯性力显著小于结构件重力,因此可以忽略惯性力作用。
3.1 腿部机构逆向动力学分析
为了简化计算, 首先利用力矩平衡原理对腿部机构进行逆向动力学分析。 将大腿机构、膝关节、小腿机构看作一个串联机构, 基于各铰接点的力矩平衡, 在以足底力为输入的情况下, 对各杆件分别进行力学分析, 计算大腿、小腿和侧摆油缸的受力情况。 图6所示为腿部机构整体、杆件ERQ、侧摆油缸的受力分析。 假设重力加速度g的方向为竖直向下。
3.1.1 大腿油缸的受力计算
将除了大腿油缸AC外的其余杆件整体作为研究对象。利用各点坐标及各杆件的长度,求解B点在腿部纵摆平面内对Yleg轴的力矩之和MB,Yleg,根据力矩平衡条件,求解大腿油缸AC的受力大小F1。在腿部随体坐标系中,B点所受力矩为
MB=BC×F1+BK×FK+∑9i=1(BPi×GPi) ,(15)
令MB,Yleg=0 ,(16)
式中:BC、BK为由B点指向C、K点的矢量;FK为足底力矢量;BPi为由B指向腿部随体坐标系中各铰接点Pi的矢量,共9个铰接点;GPi为腿部机构各铰接点处的重力矢量;下标Yleg代表取向量在腿部随体坐标系中的Yleg分量,以此类推。式(15)中假定由A点指向C点的方向为F1的正方向,除了F1大小未知,其余量均已知。
3.1.2 小腿油缸的受力计算
以杆件BCD为研究对象,求解B点在腿部纵摆平面内的力矩之和MB,BCD,Yleg,根据力矩平衡原理,求解杆件ERQ受杆件DE的力的大小FDE。此时B点所受力矩为
MB,BCD=BC×F1+BD×FDE+BD×GD+BC×GC
,(17)
令MB,BCD,Yleg=0 ,(18)
式中:BD为由B点指向D点的矢量;GC、GD分别为腿部机构杆件重力离散到关节铰接点C、D上的等效矢量。
以杆件IJK为研究对象,求解I点在腿部纵摆平面内的力矩之和MI,Yleg,根据力矩平衡原理,求解杆件IJK受到杆件JE的力的大小FJE。I点所受力矩为
MI=IK×FK+IJ×FJE+IK×GK+IJ×GJ ,(19)
令MI,Yleg=0 ,(20)
式中:IK、IJ為由I点指向K、J点的矢量;GK、GJ分别为腿部机构杆件重力离散到关节铰接点K、J上的等效矢量。
以杆件ERQ为研究对象。由受力分析可知R点在腿部纵摆平面内的力矩之和MR,Yleg,根据力矩平衡原理,求解小腿油缸QH的受力大小F2。R点所受力矩为
MR=RE×FDE+RE×FJE+RE×GE+
RQ×F2+RQ×GQ ,(21)
令MR,Yleg=0 ,(22)
式中:RE、RQ为由R点指向E、Q点的矢量;GE、GQ分别为腿部机构杆件重力离散到关节铰接点E、Q上的等效矢量。
3.1.3 侧摆油缸的受力计算
在全局坐标系中,以整个腿部为研究对象,求解髋关节侧摆支点O的力矩之和MO,Xglo,根据侧摆油缸力与足底力和腿部机构重力的力矩平衡原理,求解侧摆油缸O1N的受力大小F3。O点所受力矩为
MO=ON×F3+OK×FK+∑12i=1(OPi×GPi) ,(23)
令MO,Xglo=0 ,(24)
式中, ON、OK、OC为由O点指向N、K、C点的矢量;OPi为由O指向全局坐标系中各铰接点Pi的矢量,共12个铰接点。
3.2 腿部机构正向动力学分析
与逆向动力学分析相似,基于力矩平衡原理,对腿部机构进行正向动力学分析,即利用铰接点坐标、各杆件的重力和油缸力计算足底力[11]。分别将不同杆件作为研究对象进行力矩平衡分析,具体过程不再赘述,经分析得到求解足底力FK的方程为
-(K-I)Zglo(K-I)Xglo
-(K-B)Zglo(K-B)Xglo
0-(K-B)Zglo(K-O)Yglo
FKX
FKY
FKZ=
-
(J-I)XgloFJE,Zglo-(J-I)ZgloFJE,Xglo+(J-I)XgloGJ,Zglo+(K-I)XgloGK,Zglo
-(C-B)XgloFCA,Zglo-(C-B)ZgloFCA,Xglo+(C-B)XgloFC,Zglo+…+(K-B)XgloGK,Zglo
(N-O)Yglo F3,Zglo-(N-O)ZgloF3,Yglo+(C-O)YgloGC,Zglo+…+(K-O)YgloGK,Zglo。(25)
4 线性变换方程
虽然正向与逆向动力学分析皆基于力矩平衡原理,但是逆向动力学分析的数学方程简洁、直观,适合采用程序求解。与之相反,正向动力学分析过程复杂;而且根据分析思路,正向与逆向动力学分析需要采用不同的数学方程,编程时也需要2个完全不同的程序,不利于维护和调试。
传递矩阵法广泛应用于静力学与动力学分析,具有建模简单、使用灵活、计算效率高的优势,可以大幅度减小计算规模。由于本文中对腿部机构的正向与逆向动力学分析的数学方程可以视为线性方程组,因此借助传递矩阵法能够将腿部机构整体动力学分析离散为多个子单元的力学传递问题,推导油缸力与足底力的传递矩阵,利用矩阵相乘对腿部机构进行动力学分析,最终建立腿部机构的正-逆向动力学统一模型。
由力平衡方程可知,基于足底力、重力与油缸力的线性关系,求出足底力传递矩阵T,
T=a11a13
a21a23
a31a33 ,(26)
TFK,Xglo
FK,Yglo
FK,Zglo+
F1,g
F2,g
F3,g=F1
F2
F3
,(27)
式中:ai1、ai2、ai3(i=1,2,3)分别为在FK,Xglo、FK,Yglo、FK,Zglo作用下引起的油缸力变化的参数;(FK,Xglo, FK,Yglo, FK,Zglo)为在整机全局坐标系中的足底接触力向量;(F1,g, F2,g, F3,g)为只有重力作用下引起的油缸力变化的参数。
无论是正向动力学分析还是逆向动力学分析,都可以用方程(22)进行求解。具体求解过程如下:
步骤1 确定重力等效贡献量(F1,g, F2,g, F3,g)
和足底力传递矩阵T。
1)取(FK,Xglo, FK,Yglo, FK,Zglo)=(0,0,0),即只考虑重力作用,利用逆向动力学分析式(15)—(24)求解油缸力大小F1、F2、F3,再根据方程(27)得到重力等效贡献量(F1,g, F2,g, F3,g)。
2)分别取(FK,Xglo, FK,Yglo, FK,Zglo)=(1,0,0), (0,1,0), (0,0,1),此时不考虑重力作用,利用逆向动力学分析式(15)、(16)、…、(24)求解油缸力大小F1、F2、F3,再代入方程(27),得到由FK,Xglo、FK,Yglo、FK,Zglo引起的油缸力变化参数,即足底力传递矩阵的第1、2、3列的ai1、ai2、ai3。
步骤2 逆向动力学分析计算油缸力。将求得的足底力传递矩阵T和重力等效贡献量(F1,g, F2,g, F3,g)代入方程(27),即可求得任意重力和足底力情况时的油缸力。
步骤3 正向动力学分析求解计算足底力。将方程(27)通过变换可以得到
FK,XgloFK,YgloFK,Zglo=T-1
F1F2F3-F1,g
F2,gF3,g
。(28)
将油缸力代入线性方程(28),即可求得该状态下的足底力FK。
5 仿真实例分析
由于仅验证本文中建立的足式机器人腿部机构正-逆向动力学统一模型的有效性和可行性, 因此简化虚拟样机建模过程, 省略腿部机构各杆件的具体结构造型, 仅对杆件长度、运动副连接、驱动、质量参数等进行设置, 根据杆件长度与液压缸初始长度, 计算得出各铰接点的初始坐标, 利用Adams软件建立虚拟样机模型, 将足底力FK=(20.0, 50.0, 500.0)与初始长度分别为油缸AC长度l1=270 mm、油缸QH长度l2=310 mm、油缸MN长度l3=260 mm的3个液压缸长度作为输入量, 油缸力作为输出量, 针对油缸无作动与3个油缸分别作动一定量的4种情况进行仿真。 腿部机构虚拟样机模型如图7所示。
由于虚拟样机模型将杆件质量等效在杆件几何中心,为了减小正-逆向动力学统一模型分析计算与仿真结果的误差,需将实际质心坐标赋予虚拟样机模型。
逆向动力学仿真结果如表1所示。由表可知,正-逆向动力学统一模型与虚拟样机模型计算得到的3个油缸力的误差均小于1%,验证了本文中腿部机构逆向动力学分析的有效性。
将表1中正-逆向动力学统一模型计算得出的4种情况下的油缸力与油缸长度作为输入量, 在虚拟样机模型中将油缸力施加于油缸两端铰接点处, 足底力作为输出量, 仿真得到足底力, 结果如表2所示。 由表可知, 正-逆向动力学统一模型与虚拟样机模型计算得到的3个方向足底力的误差均小于3%, 验证了本文中腿部机构正向动力学分析的有效性。
6 结论
本文中探讨了足式机器人腿部机构的工作原理,基于力矩平衡原理,研究了腿部机构的油缸力与足底力间的数学关系,得到以下主要结论:
1)利用有限元方法建立了杆件质量离散方法,在动力学分析时有效考虑腿部机构自重,提高了动力学分析的准确性。
2)克服了机器人正向与逆向动力学分析求解过程臃肿的问题, 基于线性变换原理并结合传遞矩阵法, 融合正向与逆向动力学分析过程, 有效地简化了求解过程, 为机器人的实时控制提供了理论基础。
3)利用Adams软件建立了虚拟样机模型,对比理论方法与虚拟样机模型的输出量,验证了本文建立的足式机器人四连杆腿部机构正-逆向动力学统一模型的有效性。
参考文献:
[1]FOCCHI M, PUCCI D, PRETE A D. Editorial: bridging the gap between the lab and the real world: future perspectives for legged robots[J]. Frontiers in Robotics and AI, 2020, 7: 629002.
[2]崔敏其. SCARA机器人的拉格朗日动力学建模[J]. 机械设计与制造, 2013(12): 76.
[3]刘芳华, 马凡凡, 孙威. 三自由度并联机器人运动学和动力学建模与仿真[J]. 机床与液压, 2020, 48(23): 23.
[4]张铁, 梁骁翃, 覃彬彬, 等. 基于牛顿-欧拉法的SCARA机器人动力学参数辨识[J]. 华南理工大学学报(自然科学版), 2017, 45(10): 129.
[5]WU Y, YANG Z, FU Z, et al. Kinematics and dynamics analysis of a novel five-degrees-of-freedom hybrid robot[J]. International Journal of Advanced Robotic Systems, 2017, 14(3): 12.
[6]王超, 张文辉, 江洁, 等. 基于Matlab/Adams的工业焊接机器人运动学分析与控制联合仿真[J]. 中国工程机械学报, 2020, 18(6): 504.
[7]LUAN Y Z, GUO J M, LIU H Y. Structural dynamics simulation analysis of industrial robot arm based on Kane method[J]. Journal of Physics: Conference Series, 2021, 1871(1): 012155.
[8]AMARE Z, ZI B, QIAN S, et al. Dynamic analysis of electrohydrauliccable-drivenparallel robots[J].ProceedingsoftheInstitution of Mechanical Engineers: Part C: Journal of Mechanical Engineering Science, 2019, 233(10): 3400.
[9]王勖成, 邵敏. 有限单元法基本原理和数值方法[M]. 2版. 北京: 清华大学出版社, 1997.
[10]曾攀. 有限元分析及應用[M]. 北京: 清华大学出版社, 2004: 144-147.
[11]CHEN G,YUAN J.Nonlineardynamics analysis of shift mani-pulator for robot driver considering multiple revolute clearance joints and variable load[J]. Mechanics Based Design of Structures and Machines, 2020, 49(4): 596.
(责任编辑:王 耘)
