基于改进最小二乘支持向量机组合模型的深基坑沉降变形预测
2024-01-12刘清龙吕颖慧秦磊赵鹏
刘清龙 吕颖慧 秦磊 赵鹏


文章编号:1671-3559(2024)01-0008-07DOI:10.13349/j.cnki.jdxbn.20230320.002
摘要:为了提高深基坑沉降变形预测精度,及时为深基坑支护施工提供指导,提出一种改进最小二乘支持向量机组合模型;通过引入自适应噪声完备集合经验模态分解方法分解原始深基坑沉降变形数据,并结合粒子群优化算法和遗传算法对最小二乘支持向量机进行参数寻优,对分解的数据分别训练、预测后再叠加,得到最终预测结果;应用所提出模型对济南市某深基坑的累积沉降量进行预测,同时与其他模型对比,验证所提出模型的实用性和优越性。结果表明:所提出模型预测深基坑累积沉降量的平均相对误差为0.035%,均方误差为0.080 9 mm2,均方根误差为0.283 8 mm,所提出模型的准确性远优于其他模型的;自适应噪声完备集合经验模态分解方法的引入更有利于在深基坑沉降变形预测方面发挥最小二乘支持向量机的优势。
关键词:深基坑沉降变形;最小二乘支持向量机;经验模态分解;粒子群优化算法;遗传算法
中图分类号:TU433
文献标志码:A
开放科学识别码(OSID码):
Deep Foundation Pit Settlement Deformation Prediction Based on
Improved Least Square Support Vector Machine Combined Model
LIU Qinglong, LYU Yinghui, QIN Lei, ZHAO Peng
(School of Civil Engineering and Architecture, University of Jinan, Jinan 250022, Shandong, China)
Abstract: To improve prediction accuracy of deep foundation pit settlement deformation and provide timely guidance for deep foundation pit supporting construction, an improved least square support vector machine combined model was proposed. Complete ensemble empirical mode decomposition with adaptive noise was introduced to decompose original deep foundation pit settlement deformation data. Particle swarm optimization algorithm and genetic algorithm were combined to optimize parameters of least square support vector machine. The decomposed data were trained, predicted, and then superposed to obtain final prediction results. The proposed model was used to predict the cumulative settlement of a deep foundation pit in Jinan city, and was compared with other models to verify practicability and superiority of the proposed model. The results show that the mean relative error, mean square error, and root-mean-square error of the proposed model for predicting the cumulative settlement are 0.035%, 0.080 9 mm2, and 0.283 8 mm. The accuracy of the proposed model is far better than that of other models. The introduction of complete ensemble empirical mode decomposition with adaptive noise is more conducive to take advantage of least square support vector machine in deep foundation pit settlement deformation prediction.
Keywords: deep foundation pit settlement deformation; least square support vector machine; empirical mode decomposition; particle swarm optimization; genetic algorithm
收稿日期:2022-10-09 網络首发时间:2023-03-21T15:04:30
基金项目:国家自然科学基金项目(52108214)
第一作者简介:刘清龙(1998—),男,山东德州人。硕士研究生,研究方向为防灾减灾工程及防护工程。E-mail: 1521755399@qq.com。
通信作者简介:秦磊(1974—),男,山东济南人。教授,博士, 博士生导师, 研究方向为防灾减灾工程及防护工程。 E-mail: cea_qinl@
ujn.edu.cn。
网络首发地址:https://kns.cnki.net/kcms/detail/37.1378.N.20230320.1617.004.html
随着我国经济的高速发展,城市中的高楼大厦拔地而起,建造高层建筑时所挖的基坑也越来越深。对深基坑进行有效监测,从而为深基坑的安全提供保障和预警成为目前广泛关注的问题。
近年来,大量先进理论和技术被成功引入基坑变形预测领域[1-2],如人工神经网络[3-4]、灰色系统理论[5]、时间序列分析[6-7]和支持向量机(SVM)[8-9]等单一模型或其组合模型,但是这些预测方法要么缺少对监测数据趋势项和随机项的考虑和分析,要么适用条件特定,存在对原始数据信息挖掘不充分、预测精度有待提高以及预测效果不稳定等缺点,再加上基坑变形影响因素的复杂多样、基坑监测过程中测量误差以及其他偶然因素的存在,导致基坑监测得到的时间序列监测数据突变多,规律性较差,更加大了模型预测的难度。
为了解决已有预测方法存在的问题,提高深基坑沉降变形预测精度,本文中基于自适应噪声完备集合经验模态分解(CEEMDAN),结合粒子群优化算法(PSO)和遗传算法(GA)优化最小二乘支持向量机(LSSVM),提出改進LSSVM组合模型(简称CEEMDAN-PSO-GA-LSSVM),对济南市某深基坑的累积沉降量进行预测,并与其他预测模型进行对比,探讨所提出CEEMDAN-PSO-GA-LSSVM在实际工程中的实用性和优越性。
1 基本原理
1.1 CEEMDAN原理
CEEMDAN理论继承和发展了已有理论的优势,改进了辅助噪声加入方式,即在信号分解前添加正、负成对高斯白噪声,在每次信号分解后都对残差(RES)进行辅助噪声添加;同时,改进了分解流程,即算术平均计算的时机由CEEMDAN的全部信号分解完成后,转移到信号的每个分解阶段。这些改进保证了CEEMDAN的每个本征模态函数(IMF)含有较小的噪声幅值,重构误差也维持在较小的范围[10-12]。
设S(t)为待处理时间序列信号,t为时间;利用CEEMDAN所得的第k个IMF分量为fIMF,k;定义操作符Ek(·),对于给定的信号,可以用经验模态分解(EMD)得到给定信号的第k个IMF分量;ωi为服从标准正态分布N(0,1)的高斯白噪声, εi为添加高斯白噪声的标准差,i=1,2,…,I, I为添加高斯白噪声的总次数,则CEEMDAN算法步骤[13]如下:
步骤1 利用集合经验模态分解(EEMD)得到第1个IMF分量为
fIMF,1(t)=1i=1 f(i)IMF,1 (t) 。(1)
步骤2 在k=1时的第1个阶段计算第1个余量
R1(t)=S(t)-fIMF,1(t) 。(2)
步骤3 分解R1(t)+ε1E1(ωi )(i=1,2,…,I),到第1个IMF分量,则第2个IMF分量为
fIMF,2(t)=1i=1E1[R1(t)+ε1E1(ωi )] 。(3)
步骤4 对于k=2,3,…,M(M为分解的总次数),计算k次分解后的第k个余量
Rk(t)=Rk-1(t)-fIMF,k(t) 。(4)
步骤5 分解Rk(t)=εkE1(ωi )(i=1,2,…,I)到第k个IMF分量,则第k+1个IMF分量为
fIMF,k+1(t)=1i=1Ek[Rk(t)+εkEk(ωi )]。(5)
步骤6 将k+1返回步骤4, 重复步骤4、5、6, 直到当残余分量不能再分解时停止分解, 最终的余量为
R(t)=S(t)-∑Mk=1 fIMF,k ,(6)
此时待处理信号为
S(t)=R(t)+∑Mk=1 fIMF,k 。(7)
1.2 LSSVM原理
LSSVM是SVM的变形和改进。LSSVM在SVM的基础上,将复杂的二次规划问题转为求解线性方程组的问题,大幅提高了求解效率,同时也提高了预测精度[14-15]。主要改进体现在将经验风险由1次方变为2次方,用等式约束代替不等式约束,设样本x=(x1,x2,…,xJ), y=(y1,y2,…,yJ), J为样本个数,并考虑到可能存在预测误差,引入非负的松弛因子ξ=(ξ1,ξ2,…,ξJ),则LSSVM优化问题的最小化函数[16]为
minΦ(ω,ξ)=12ω2+γj=1ξ2j ,(8)
约束条件为
yj-ωTφ(xj )=b+ξj, j=1,2,…,J ,(9)
式中:ω为权向量;φ(·)为非线性映射函数,可将输入样本映射到高维特征空间;b、γ分别为待定参数、惩罚系数,取值均大于0;·为欧氏范数运算符。
根据式(8)、(9)建立拉格朗日方程式求解,并定义核函数K(xg, xh )=φ(xg )φ(xh ),(g,h=1,2,…,J),得到LSSVM回归函数模型为
y(x)=∑Jj=1ajK(xj, x)+b ,(10)
式中:aj为拉格朗日乘子;较常用的核函数是高斯径向基函数K(xg, xh )=exp-xg-xh22σ2,其中σ为核参数。
惩罚系数γ和核参数σ是LSSVM的2个重要参数。γ又称为成本参数,取值过大会使LSSVM对数据过拟合,取值过小又会导致欠拟合;σ决定了支持向量的个数,而支持向量的个数又影响LSSVM训练和预测速度,因此如何选取合适的模型参数使LSSVM实现高效准确预测是一直被关注的问题。
1.3 PSO与GA
PSO是一种源于鸟类群体觅食行为特征研究而演化出的全局优化算法。PSO将待优化问题的每种解简化为粒子,每个粒子的位置即为问题的一种可能解,通过每次迭代,最优粒子共享信息,促使所有粒子均向最佳位置移动,最终获得最优解[17]。
GA是通过模拟自然界中种群的优胜劣汰和变异进化的演化模式而提出的一种优化算法。GA将待解决的问题按一定的规则编码成由若干基因组成的染色体,众多染色体组成算法的种群,在不断迭代的过程中模仿自然遗传原理,通过对染色体的选择、交叉和变异等操作,使种群得到进化,进而达到逼近最优解的目的[18-20]。
2 模型建立
2.1 数据预处理
为了最大限度地减少原始数据中随机因素的影响,同时避免原始数据中有效信息的丢失,本文中利用CEEMDAN方法将原始数据分解为有限个IMF分量和1个残差余量。每个IMF分量为独立且富有规律的周期信号,反映了数据的随机特征,残差余量为光滑趋势明显的低频信号,反映了信号的趋势特征,经过处理的信号更有利于LSSVM进行预测。
2.2 PSO-GA参数寻优
利用LSSVM预测由CEEMDAN分解得到的IMF分量和残差余量。LSSVM的预测精度受惩罚系数γ和核参数σ的影响很大,需要借助优化算法为LSSVM选取参数。
PSO作为常用的优化算法,结构简单,运行效率高且具有记忆能力,但是在寻优时易导致局部最优解。在GA中,经过选择、交叉和变异等操作可以提高种群的多样性,保证了算法的全局寻优能力,但是相对于PSO,GA收敛较慢[21]。为了综合PSO与GA的优势,弥补双方的不足,本文中将二者结合,建立PSO-GA,对LSSVM进行参数选取,步骤如下:
步骤1 初始化种群。先随机生成种群与速度的实数序列,每个个体有2个参数,即惩罚系数γ与核参数σ,计算种群的适应度。采用3折交叉验证下均方误差(MSE)的均值作为PSO-GA寻优过程中的适应度函数,这样的修改比只采用MSE更能兼顾LSSVM的训练和预测水平。
步骤2 种群编码。原始的GA编码方式是利用MATLAB工具箱中的GA函数,先随机生成二进制串,然后将二进制串一一对应到实值,以保证种群的随机性,但缺点是只能实现二进制串向实值的单向转换,不能实现双向操作且精度不能控制。本文中根据浮点编码的要求,重新编写一组能控制数据精度编码与解码函数,有效解决了PSO-GA中PSO与GA在种群形式上的接续问题。
步骤3 接入GA对种群进行选择、交叉、变异操作。
1)选择操作。选择操作采用优胜劣汰策略。首先将种群个体按适应度从小到大的顺序进行排列,前10%(可自行设定)的种群个体直接复制到下一代,然后再利用select(·)函数,在全体种群中根据预定比例,随机选出对应个数的种群个体进行交叉操作。选择过程中适应度越大的个体越容易被选中,并且有被重复选中的可能。
2)交叉操作。交叉算子采用单点交叉的操作,即在染色体上随机选择1个交叉点,将2条染色体交叉点后的部分进行交换。为了避免后期优秀个体因交叉操作而被破坏,设置自适应交叉因子,即随着迭代次数的增加,按照本代在总体迭代次数的位置,选择合适的交叉概率,迭代次数越接近终止迭代次数,交叉概率越小。交叉操作公式[22]为
p=pmin+(pmax-pmin)1-qqmax ,(11)
式中:p為当前交叉概率;pmin 、pmax分别为交叉概率的最小值、最大值;q为迭代次数当前值;qmax为迭代次数目标值。
3)变异操作。由于在GA中采用的编码方式是浮点编码,即用二进制串表示种群个体,因此变异操作完全模仿自然基因的变异方式,通过随机地将某个体的某基因由0突变为1或由1突变为0实现变异操作。
步骤4 将GA处理的种群按照PSO粒子更新公式进行速度和位置更新,然后再进行一次适应度计算。
步骤5 迭代寻优。重复步骤3、4,通过将每个粒子的适应度与个体最优Pbest和全局最优Gbest进行比较,寻找更优秀的个体,同时更新Pbest和Gbest。当迭代次数或解的精度达到要求后终止循环,输出最优解。
2.3 预测结果输出
将LSSVM对IMF分量与残差余量的预测结果反归一化处理后进行叠加,得到深基坑监测数据的最终预测结果。
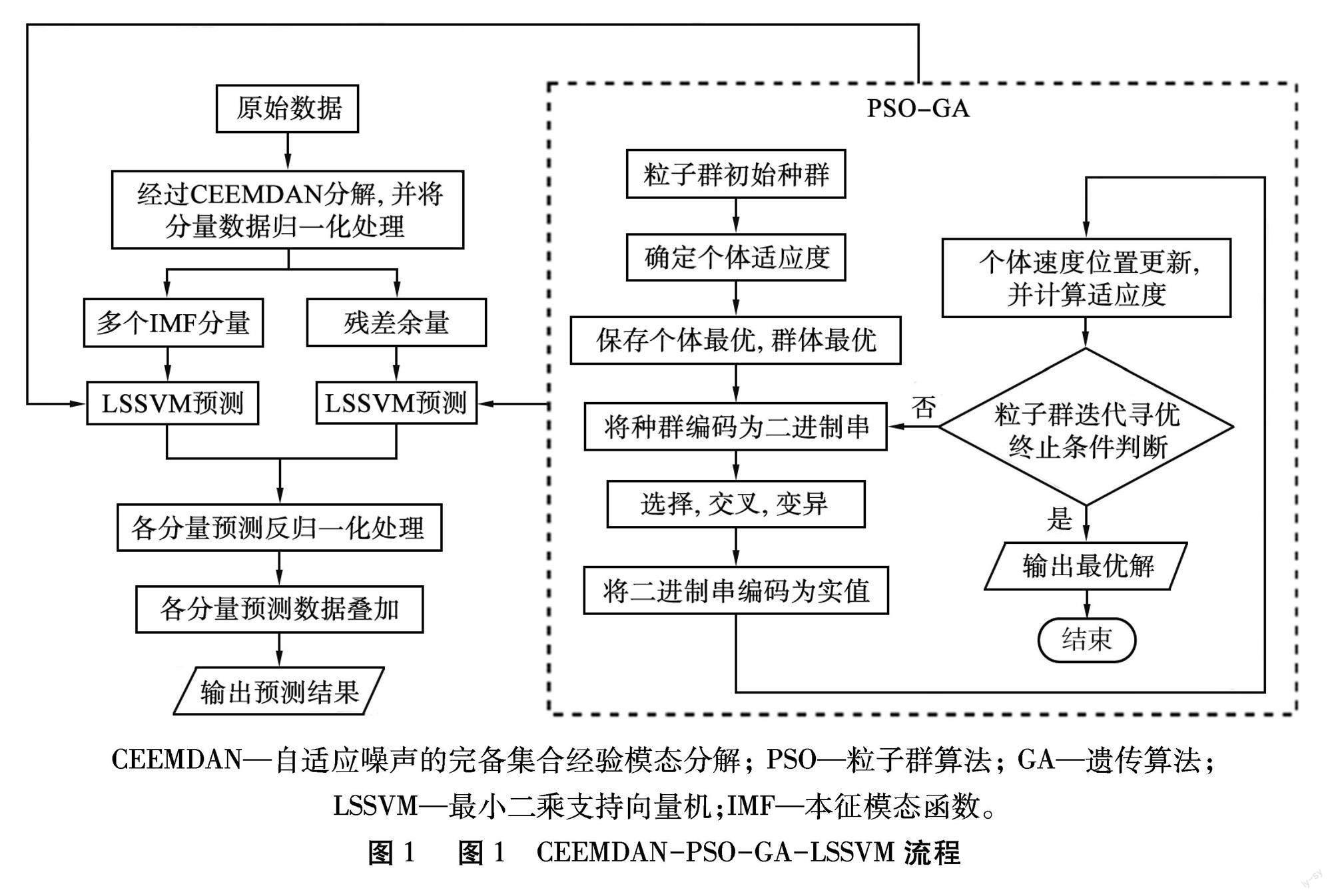
综上,经过数据预处理、PSO-GA参数寻优及最终结果输出,建立CEEMDAN-PSO-GA-LSSVM,流程如图1所示。
3 实例分析
3.1 工程概况
利用本文中提出的CEEMDAN-PSO-GA-LSSVM,对济南市某深基坑监测点Y7的累积沉降量进行预测。该监测点所在基坑剖面采用格构式锚杆挡墙支护形式,深度为18.15 m。
以监测点Y7前28 d数据作为训练样本, 剩余5 d数据作为预测样本。 监测点Y7的累积沉降量如图2所示。从图中可以看出,监测点Y7的累积沉降量呈现递增的趋势,最大累积沉降量为27 mm,略小于该基坑剖面预警值30 mm,说明对深基坑进行沉降变形预测非常必要。
3.2 数据处理
CEEMDAN对监测点Y7的累积沉降量分解结果如图3所示。 从图中可以看出:CEEMDAN将原始数据分解为1个IMF分量和1个残差余量。 fIMF,1波动变化较大,属于高频分量;残差变化稳定, 线条光滑,属于低频分量。
3.3 PSO-GA参数寻优与LSSVM预测
利用PSO-GA优化的LSSVM对IMF1和残差进行预测。PSO-GA的初始参数设置如下:最大迭代次数为200, 种群个数为20, 交叉概率范围为[0.1,fIMF,1—利用CEEMDAN所得的
第1个本征模态函数(IMF)分量。
0.9],惩罚系数γ范围为[0.001, 100],核参数σ范围为[0.1, 5 000],局部搜索能力为1.5, 全局搜索能力为1.7。
在基于fIMF,1和残差参数的寻优过程中, 得到LSSVM相应的最优参数为γ1=2 517.522 5, σ1=12.468 2;γ2=3 141.954 6, σ2=0.233 64。经PSO-GA优化的LSSVM对fIMF,1和残差的拟合与预测结果如图4所示。将fIMF,1和残差的拟合与预测数据反归一化处理后再叠加,得到最终预测结果。CEEMDAN-PSO-GA-LSSVM对监测点Y7的累积沉降量拟合与预测结果如图5所示。
从图4中可看出:fIMF,1变化波动较大,不易拟合,但变化范围很小。拟合MSE为0.060 90 mm2,预测MSE为0.017 1 mm2,整体误差在许可范围之内。相比之下,残差的拟合与预测曲线与原始数据相差较小,误差也保持在一定精度范围内。由图5可得,CEEMDAN-PSO-GA-LSSVM累积沉降量预测最大误差为0.43 mm,最小误差为0.03 mm,均在许可范围之内,说明本文中所提出的模型在深基坑沉降变形预测方面具有实用性。
3.4 模型分析
为了验证本文中所提出CEEMDAN-PSO-GA-LSSVM的优越性,在与3.3节中参数设置相同的条件下,用PSO、GA和本文中所建立的PSO-GA这3种优化算法对LSSVM进行参数选取,得到PSO-LSSVM、GA-LSSVM和PSO-GA-LSSVM这3种模型, 并利用它们直接对监测点Y7的累积沉降量进行预测, 同时与本文中所提出的CEEMDAN-PSO-GA-LSSVM的预测效果对比。
(a)fIMF,1
(b)残差
fIMF,1—利用自适应噪声完备集合经验模态分解所得的第1个本征模态函数(IMF)分量。
3.4.1 PSO-GA优化效果
PSO、GA和本文中所建立的PSO-GA这3种算法在相同参数条件下优化LSSVM的适应度曲线如图6所示。由图可知:PSO在寻优过程中适应度曲线下降波动很大,很快得到一个适应度较小的解,表明计算效率很高,但是在第40代后趋于平稳而不再变化,陷入局部最優;GA在寻优过程中转折点较多, 表明具有较强的全局搜索能力, 在第1~40代时表现出较强种群多样性, 在之后的种群迭代过程中, 种群多样性明显减弱;PSO-GA的适应度曲线呈多阶梯状下降, 适应度最终值为0.093 5, 在3种优化算法中适应度最小, 表明PSO-GA在跳脱局部极值、挖掘新优解等方面具有优异的性能。
3.4.2 CEEMDAN-PSO-GA-LSSVM预测效果
4种模型对监测点Y7累积沉降量的预测结果如图7所示。 以平均相对误差(MRE)、均方根误差(RMSE)和MSE作为模型的预测精度评价指标, 结果如表1所示。 从图7中可以看出, 相对于其他3种预测模型, CEEMDAN-PSO-GA-LSSVM的累积沉降量预测曲线更贴近于真实数据。 由表1可得, CEEMDAN-PSO-GA-LSSVM预测累积沉降量的MRE为0.035%, MSE为0.080 9 mm2, RMSE为0.283 8 mm, 精度高于其他预测模型的。 由此可知:本文中提出的CEEMDAN-PSO-GA-LSSVM预测精度更高, 整体效果优于其他3种模型的, 经过CEEMDAN处理的数据, 更便于LSSVM模型在训练阶段寻找规律,拟合曲线;同时也最大限度地避免了有用信息的丢失,从而得到更优的预测效果,因此CEEMDAN-PSO-GA-LSSVM在深基坑沉降变形预测方面具有一定的优越性。
PSO—粒子群优化算法;LSSVM—最小二乘支持向量机;
GA—遗传算法;CEEMDAN—自适应噪声
完备集合经验模态分解。
4 结论
本文中提出一种改进LSSVM组合模型进行深基坑沉降变形预测。通过CEEMDAN分解监测点数据,再利用PSO-GA优化的LSSVM对分解得到的IMF分量和残差余量进行预测,将预测结果叠加,得到最终的预测结果。通过不同模型的对比得出以下主要结论:
1)将深基坑累积沉降量通过CEEMDAN处理后能得到相对平稳的残差曲线,更有利于LSSVM对数据规律的学习,进而提高了预测精度;同时,对其他IMF分量的预测也减少了原始深基坑沉降变形数据中有用信息的丢失,从而达到更综合、有说服力的预测效果。
2)本文中所提出的CEEMDAN-PSO-GA-LSSVM对监测点Y7的累积沉降量预测结果在MRE、MSE、RMSE指标方面明显优于其他3种模型的。由此可见,本文中对GA遗传因子的改进以及对PSO、GA算法结合方式的优化大幅增强了算法的全局寻优能力,同时也改善了算法寻优的稳定性。
3)本文中对深基坑沉降变形的预测仅针对现场的沉降监测数据,并未考虑工况、土体参数、支护形式等因素的影响。要得到更精确、可靠的预测结果,应尽可能多地综合考虑各种影响因素,这将是深基坑沉降变形预测研究的必由之路。
参考文献:
[1]管志勇, 田永军, 戚蓝. 综合模拟和预测方法在工程沉降中的应用[J]. 合肥工业大学学报(自然科学版), 2007, 30(6): 765.
[2]王兴科, 王娟. 基于优化支持向量机-混沌BP神经网络的基坑变形预测研究[J].隧道建设, 2017, 37(9): 1105.
[3]赵贞. 基于BP神经网络的基坑变形预测应用研究[J]. 山西建筑, 2022, 48(8): 160.
[4]梁磊. 基于BP神经网络及其改进算法的地铁基坑变形预测研究[D]. 西安:长安大学, 2021.
[5]卢彬, 冯现大, 鲁瑞. 基于灰色组合模型预测隧道围岩收敛变形[J]. 济南大学学报(自然科学版) , 2022, 36(6): 689.
[6]金路, 姜谙男, 赵文.基于差异进化支持向量机的基坑变形时间序列预测[J]. 岩土工程学报, 2008, 30(增刊1): 216.
[7]阿丽米拉·艾力. 基坑变形监测数据处理及预测模型研究[D]. 乌鲁木齐: 新疆大学, 2021.
[8]徐洪钟, 杨磊. 基于最小二乘支持向量机回归的基坑变形预测[J]. 南京工业大学学报(自然科学版) , 2008, 30(2): 51.
[9]王鹏程. 基于LSSVM的地铁车站基坑周边建筑物的沉降规律与预测研究[D]. 阜新: 辽宁工程技术大学, 2016.
[10]MANDIC D P, REHMAN N U, WU Z H, et al. Empirical mode decomposition-based time-frequency analysis of multivariate signals: the power of adaptive data analysis[J]. IEEE Signal Process Magazine, 2013, 30(6): 74.
[11]任子晖, 成江洋, 邢强, 等. 基于CEEMDAN与Teager能量算子的谐波检测方法[J]. 电力系统保护与控制, 2017, 45(9): 56.
[12]宋启航. 基于模态分解技术的地震信号去噪方法研究[D]. 大庆: 东北石油大学, 2020.
[13]胡勇平. 基于CEEMDAN-PSO-LSSVM模型的基坑變形预测研究[D]. 呼和浩特: 内蒙古农业大学, 2018: 42.
[14]HUANG X L, SHI L, SUYKENS J A K. Asymmetric least squares support vector machine classifiers[J]. Computational Statistics & Data Analysis, 2014, 70: 395.
[15]SUYKENS J A K, VANDEWALLE J, DE MOOR B. Optimal control by least squares support vector machines[J]. Neural Networks, 2001, 14(1): 23.
[16]林楠, 李伟东, 张文春, 等. 最小二乘支持向量机在深基坑变形预测中的应用[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(11): 1472.
[17]BLACKWELL T, KENNEDY J. Impact of communication topology in particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(4): 689.
[18]闻新超, 周琳霞, 牛凯. 一种基于混合编码的遗传算法[J]. 电子技术, 2003(1): 60.
[19]BOOKER L B, GOLDERG D E, HOLLAND J H. Classifier systems and genetic algorithms[J]. Artificial Intelligence, 1989, 40(1/2/3): 235.
[20]倪全贵. 粒子群遗传混合算法及其在函数优化上的应用[D]. 广州: 华南理工大学, 2014.
[21]孙洁, 崔婷婷, 刘晓悦, 等. PSO-GA优化ELM的高炉铁水硅含量预测[J]. 机械设计与制造, 2022(3): 228.
[22]刘家奇, 余朝刚, 朱文良. 基于改进PSO-GA算法的轨道精调优化研究[J]. 智能计算机与应用, 2021, 11(12): 80.
(责任编辑:王 耘)
