非冷链商品配送路径优化研究——以京东配送为例

梁力军，袁苗苗，孙玉璇 LIANG Lijun, YUAN Miaomiao, SUN Yuxuan

（北京信息科技大学 信息管理学院，北京 100192）

0 引 言

物流车辆路径研究中，带时间窗的车辆路径问题是当前学界的关注重心；同时，关于车辆路径优化的算法方面也受到学界的重点关注。首先，带时间窗的车辆路径问题基于单纯的车辆路径问题（VRP） 外，补充顾客满意的服务访问时间窗口，拓展了VRP 的研究。另外，据此合理规划路线是提高物流服务质量和提升经济效益的重要手段。具有顾客限定的服务时间窗口早在20 世纪80 年代末就已经被引入到车辆路径问题研究中，如Solomon 在研究中考虑了顾客要求的时间窗口，以解决车辆的配送问题，同时为路径分析拓展了新的研究思路[1]。现实生活中，由于部分商品自身具有强时效性，如生鲜农产品等，因此，考虑到带时间窗口因素约束的研究也逐渐增多，如刘炎宝等[2]、范厚明等[3]、葛显龙等[4]、酒艳妮等[5]均围绕具有时效性要求的生鲜产品及外卖配送路径最优化展开了相关探究。

遗传算法和变邻域搜索算法在解决路径优化问题上的应用较为成熟。Holland 最早提出遗传算法，该算法以达尔文的物种演化原理为基础，利用选择、交叉、变异等方法，模拟自然界中的遗传机理，寻求最优，是一种具有全局随机寻优能力的仿生生物的自然演化模型[6]；然而，经过王芳等[7]、成冲等人[8]在配送路径相关研究中证实，遗传算法得出的结果时常陷入局部最优，未能寻到最优的结果。由Ghosh 和Shan[9]提出的变邻域搜索算法是一种局部搜索方法，具有通过变换邻域位置不断提高局部搜索能力，从而不会过早陷入局部优化。学术界内诸多学者都在不断尝试探索寻找最优的算法求解车辆路径问题，从相关研究来看，改进后的变邻域搜索算法与遗传算法要比传统算法呈现出的结果更优。如李丹莲等[10]、张铎等人[11]提出多色体遗传算法、多准则决策遗传算法等解决路径优化问题，最终结果验证了优化后算法的。Renata[12]提出了一种基于NSGAt 的变邻域多目标遗传算法，结果表明，所提出的VN-MGA 算法优于纯VNS 算法；宋强等[13]在解决多行程车辆路径问题上采用了多种算法，其中改进的变邻域搜索算法与包括传统变邻域搜索等其他算法相比，其结果更优；王伟权等[14]基于改进变邻域搜索算法中由启发式算法构造出初始解，进而进行变邻域搜索的算法求解，验证出用该算法解决车辆配送路径问题比其他算法能大幅降低物流成本。

综上所述，学者用不同的算法围绕服务时间窗口和商品的配送进行了相关研究，但存在一定的局限性。一是，相关研究对象主要集中于具有时效性要求的冷链生鲜产品、医药产品、外卖配送等展开，而面向非时效性的研究较为匮乏。二是，在车辆路径问题中，改进后的算法与传统遗传算法和变邻域搜索算法相比，呈现出的结果更优。

1 本文物流配送路径问题描述及建模

本文将研究对象转向非冷链生鲜产品，即将变邻域搜索算法与遗传算法进行融合，构建起一种新型变邻域遗传搜索算法，将配送总成本、顾客缺货惩罚成本等纳入目标函数模型，探究新模型能否有效解决遗传算法结果陷入局部最优的问题，以试图解决车辆路径的最优选择问题。具体步骤如下：

1.1 问题描述与假设

研究以单点配送中心向周边多个客户需求点配送商品为例，来研究配送服务车辆路径选择问题。当配送中心收到客户需求点的线上需求订单后，对订单进行快速响应，并根据需求点的时限要求和配送车辆、配送路径等因素，部署相关配送服务行为。本文相关假设如下：

假设1：单点物流配送中心和各客户需求点地理位置已知。

假设2：客户的需求量、期望的配送服务时间以及迟到惩罚成本已知。

假设3：实施配送任务的车辆车型相同，每辆配送车的最大承载能力已知，每辆配送车所服务的客户需求总量之和不超过车辆的最大承载能力。

假设4：配送车辆的行程速度均衡且为定值，暂不考虑配送道路中车流量及路况的限制。

假设5：每个客户需求点由一辆配送车实施配送，而每辆车可向多个客户需求点实施配送。

假设6：每辆配送车辆配备一名配送人员，人员成本为定值。

1.2 模型相关参数设定

本文所构建的配送路径优化模型的参数变量如表1 所示，并以成本作为评估配送路径优化模型效果的指标。

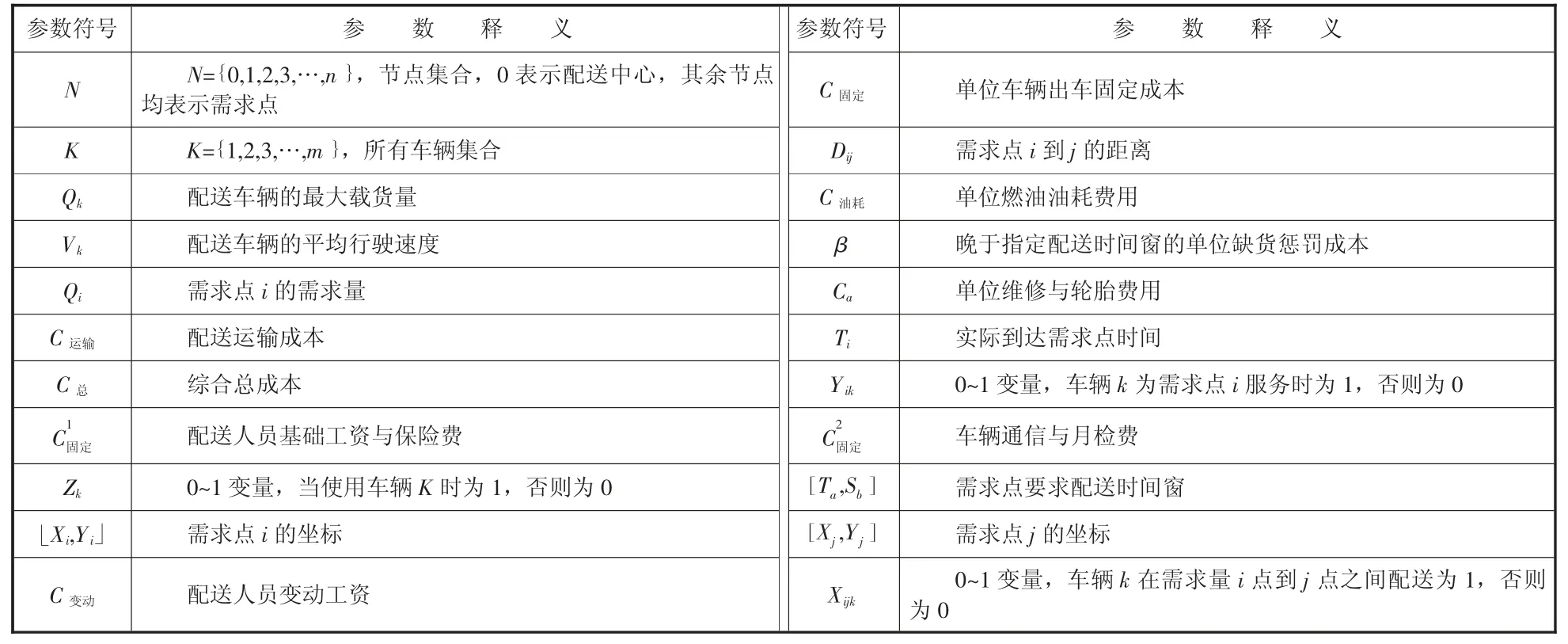
表1 模型参数设定与释义

由表1 可知，物流配送模型的变量主要包括运输总成本C总、配送运输成本C运输、配送人员变动成本C变动等。其中运输总成本由固定成本C固定、配送运输成本C运输和缺货惩罚成本W 三大部分构成。配送运输成本C运输与运输路程紧密关联，不同的运输路径造成配送运输成本C运输的变动；配送人员变动成本C变动和车辆行驶路程有关，单位距离变动成本固定，行驶里程根据不同的行驶路线来决定。

1.3 相关成本分析

本文将配送路径优化模型的成本分为三个部分：一是配送车辆的出车固定成本；二是配送车辆的配送运输成本；三是缺货惩罚成本，即因配送未满足时限要求而导致客户需求点发生缺货所产生的损失。

（1） 车辆出车固定成本。单车固定成本主要包括车辆通讯费、月检费、驾驶员基本工资和保险费等。固定成本总费用与驾驶人员及配送车辆的数量相关，计算公式如式（1） 所示。

（2） 配送运输成本。为便于研究，假设配送网络中两个位置之间的距离是根据欧几里德线性距离计算所得，Dij定义为从位置i 到位置j 的线性距离，如式（2） 所示，车辆配送运输总成本计算公式如式（3） 所示。

（3） 缺货惩罚成本。假设客户需求点的配送限定时间为[Ta,Sb]，Ta代表需求点能接受的最早配送时间，Sb代表需求点能接受的最晚服务时间。如在限定时间内完成配送，则不发生惩罚成本；反之则产生惩罚成本，且惩罚成本由配送不及时给需求点实际造成的缺货损失决定。

客观而言，配送时间的提前或延迟均会对客户需求点产生负向影响，但研究对象主要针对非生鲜产品，故忽略配送时间提前而产生的惩罚成本。惩罚成本计算公式如式（4） 所示。

1.4 物流配送路径模型构建

在分析相关成本后，总配送成本的计算公式如式（5） 所示。

式（5） 表示的配送总成本，包括配送车辆的使用成本、运输成本、超出规定服务时间窗的惩罚成本。

相关约束条件如下：

式（6） 表示车辆k 的最大限制容量能满足服务对象需求点的需求量；式（7） 表示对服务每个需求点的车辆进行了限制，一个服务需求点只能安排一辆车进行服务操作；式（8） 表示车辆从配送中心启动并最终返回配送中心。

Ti>Sb时：

式（9） 表示超出顾客规定服务时间窗口的惩罚成本。

否则：

式（10） 表示送货到达时间若早于规定的服务时间窗口，则惩罚成本为0，即不会产生惩罚成本；式（11） 表示车辆k 在行驶过程中到达服务需求点j 的时间等于车辆到达服务需求点i 的时间加上在i 点服务的时间g 再加上从i 点行驶到j 点消耗的时间；式（12） 表示到达各个服务需求点的车有且仅有一辆。

2 变邻域遗传搜索算法求解

本文所运用的变邻域遗传搜索算法在车辆调度应用[15]、车辆路径分析[16]、货架分配方法[17]、车间物流调度[18-19]等方面的研究中已较为成熟，能够解决区域配送路径的相关问题，且在算法上效率更高，求解的质量更优。另外，相关学者已将该算法用于生鲜冷链配送路径的研究[20]。

因此，本文将其应用于物流车辆的配送领域，针对附带时间窗的配送路径优化问题，运用MATLAB 软件和优化后的变邻域遗传搜索算法来实现求解，从而实现车辆配送路径的优化。变邻域遗传搜索算法的实现流程如图1 所示。

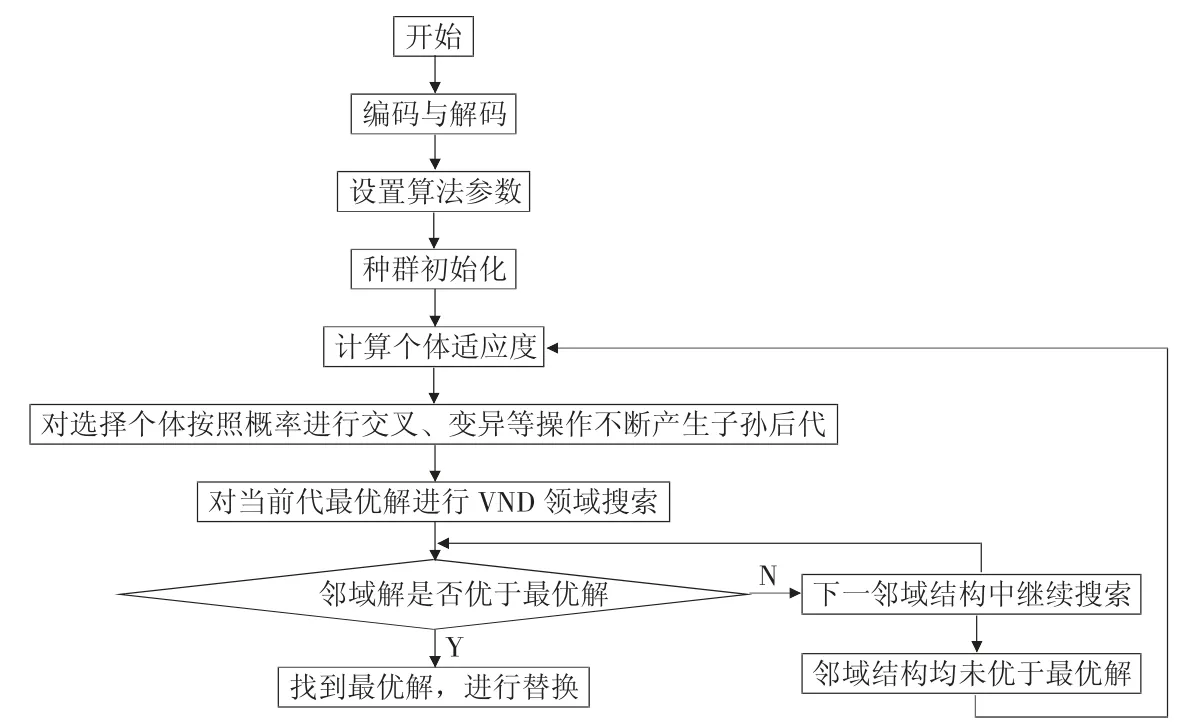
图1 变邻域遗传搜索实现流程

2.1 编码与解码

（1） 编码与解码。路径优化问题有两种主编码方法：路径表示法和邻接表示法。为直观表达，研究采用路径表示法。假设共有7 个便利店需求点（用数值1~7 表示），1 个配送中心（用0 数值表示），外加3 辆配送车辆，整个配送过程中的配送路径从配送中心0 开始出发，最终再返回到配送中心0 结束。例如：若最终生成的编码为：0,1,3,0,5,7,2,0,4,6,0。则该编码主要构成三条不同的配送路径，分别为：0→1→3→0；0→5→7→2→0；0→4→6→0。

（2） 种群初始化及适应度函数。为了确保个体的多样性，通过随机生成的方式生成原始种群。若将原始种群的规模大小设定为N，则原始种群的第一代种群由N 个个体构成，N 个个体分别对应表示有N 个初始解，且在未进行遗传演化之前，原始种群内的个体适应性是比较低的。群体的个体品质通常是以适应度值来衡量，如果一个染色体对应的路径选择成本较低，那么相应的解决方案就会有更高的适应度，并且随着相应方案成本的减少，其适应度也会随之增加。该方法以物流总成本和便利店缺货损失成本为目标函数，并以此进行优化。

2.2 遗传算子

遗传算子主要包括选择、交叉、变异三个部分。

（1） 选择算子。通过选择轮盘赌的形式选择出算子，通过这种形式可以更大的概率选择质量较高的个体。思路如下：

首先，将种群中的个体纳入适应度函数，分别计算适应值fi和整体适应值F 值。

其次，计算出从种群整体中选择出个体i 的概率pi，计算公式为：

再次，计算选择累计的概率Pi, 计算公式为：

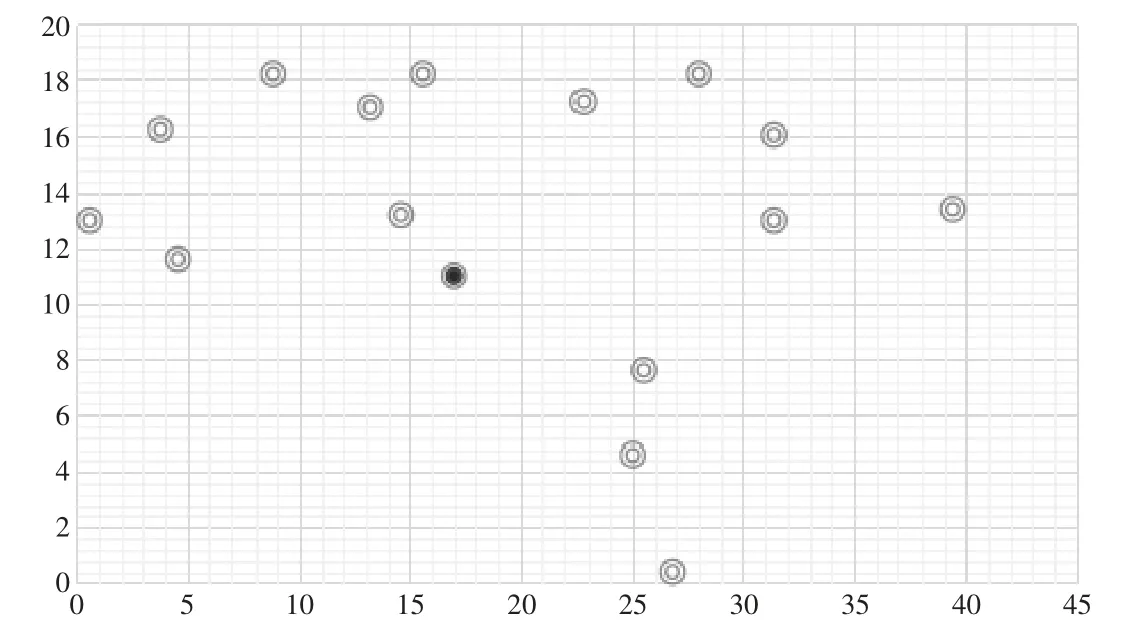
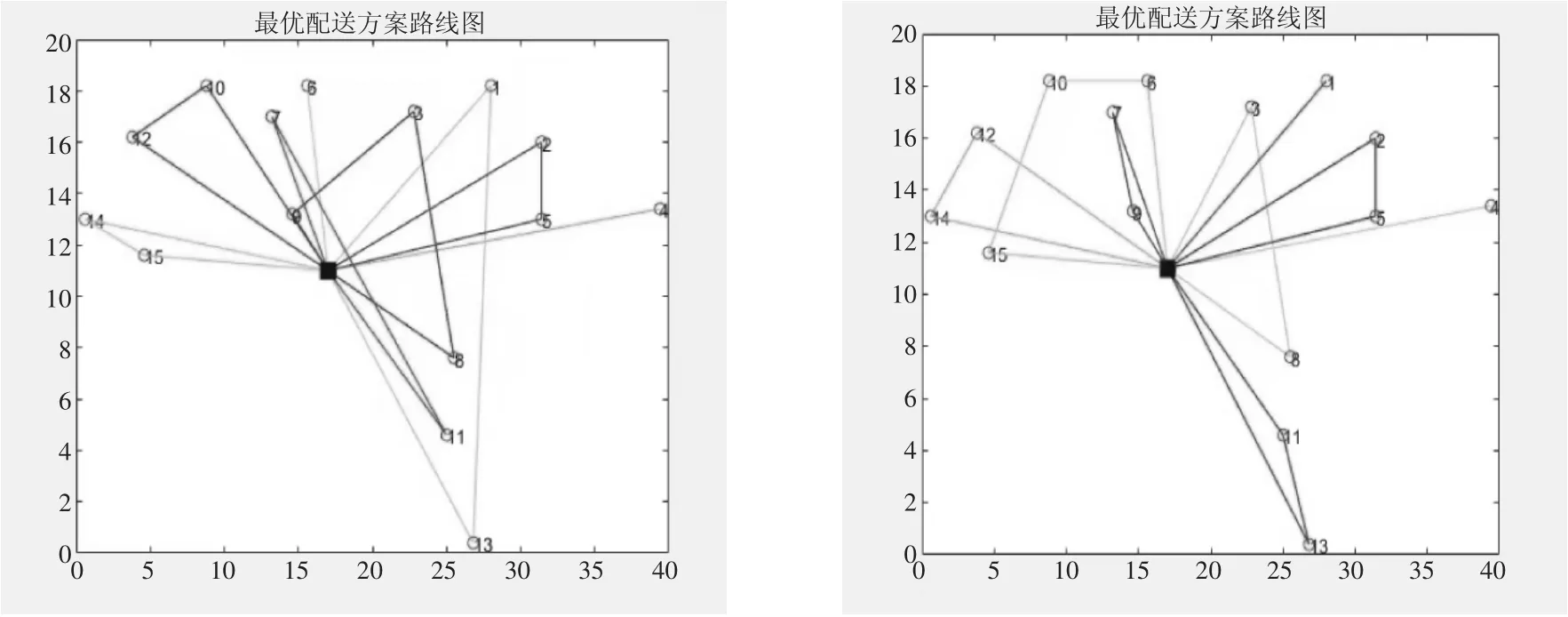
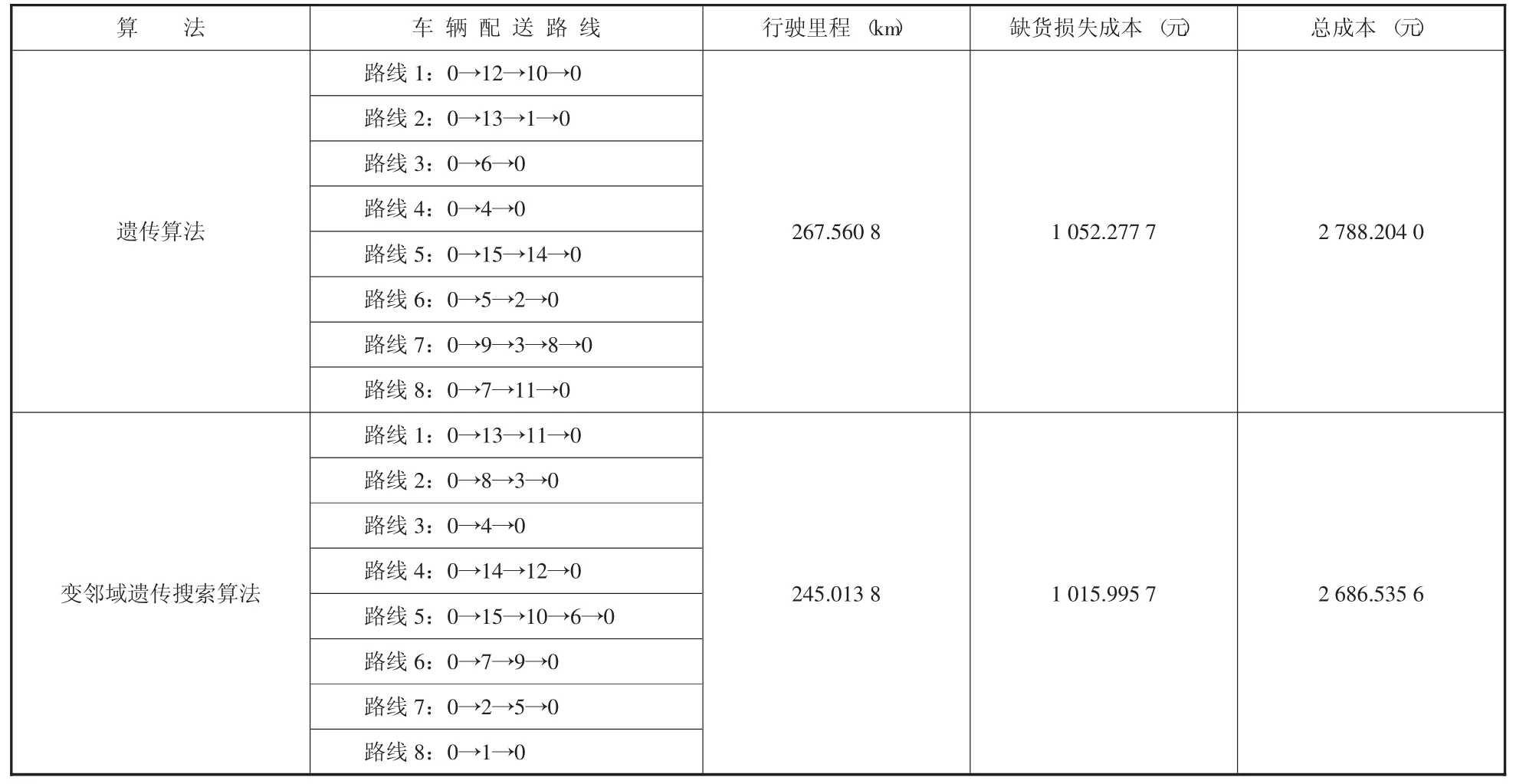
下一步，生成随机数n，n 存在于0~1 之间，当随机数n

最后，不断进行群体大小的次轮盘赌，以产生下一代群体。

（2） 交叉算子。交叉操作能够保持父代个体的中优良特性的同时提高全局搜索的能力，为了防止交叉过程中出现重复的个体，提出了交叉算子，即先生成两段交叉区间的端点，然后把交换后的基因序列交叉到另一条染色体的前端，把原来的基因序列中的重复的基因剔除掉，从而形成新的后代。其过程示例如图2 所示。

图2 交叉算子过程示意图

（3） 变异算子。变异操作可以弥补交叉操作过早收敛，陷入局部优化的缺陷。本文选择Swap 算子作为变异算子，在群体中随机选择个体，并随机选择两个突变的基因进行交换操作以形成新的个体。例如：变异前：2 6 4 1 3 5 8 7 1 5，变异后：2 6 4 8 3 5 1 7 1 5，可发现基因1 与基因8 进行了位置互换。

2.3 邻域结构

本文主要采用逆序变化和互换变化两种邻域结构进行搜索，两种邻域结构的变化如图3 所示。

图3 邻域结构变化示意图

2.4 终止条件设定

当迭代进化数达到预先设定的最大进化代数时，算法停止循环运行，最终拥有最大适应度值的个体作为最优解输出。

3 算例分析

本文参考京东北京K 配送中心为周边便利店配送便利商品需求的历史数据[21]，设产生合理的便利店配送需求为Qi，且单个便利店的需求量不超过京东配送中心车辆的最大载重量；该配送中心使用车型为江淮帅铃H 载货车来向周边便利店需求点进行配送服务，且其自有6 辆配送车辆，车速Vk一般为40~80km/h，最大运载量Qk为1 吨，单位燃油油耗费用C油耗为1.5 元/公里，单位维修与轮胎费用Ca为0.8 元/公里，配送人员基础工资为100 元/每辆/每天，车辆的通信及月检费为20 元/每辆/每天，车辆配送人员的可变工资为C变动为0.6 元/公里。

假设单位缺货惩罚成本为2 元/min，配送车辆每天早上7 时出发，每个便利店服务停留时间不超过半小时。K 京东配送中心由于向周边服务的门店较多，数据分析比较困难，因此本文选定了周边固定区域的15 家便利店作为研究样本，算法中相关参数经过不断调试最终设置如表2 所示。

表2 算法相关参数设置

通过整理坐标、各个便利店需求点的需求量及所要求的配送服务时间窗，得到所有需求节点的相关信息如表3 所示，为了获得更清晰直观的路线图，给定便利店需求点的序号为1~15，京东配送中心点的序号用0 表示。

表3 配送中心、便利店需求点相关数据

为了便于计算众多需求点及配送中心点之间的空间距离，将配送中心与便利店需求点的实际具体位置映射到平面上，形成横纵（X, Y ）坐标点分布如图4 所示，其中红色实心点为配送中心。

图4 配送中心和需求点坐标的位置

本文利用MATLAB R2018a 软件，结合上述实例数据，分别用传统的遗传算法和变邻域遗传搜索算法进行了求解，并给出两种算法的最优路线图分别如图5 所示，最优车辆配送路线、综合总成本如表4 所示。

图5 传统遗传算法（左） 和变邻域遗传算法（右） 最优路径图

表4 车辆配送最优路径图

由结果可以看出，变邻域遗传搜索算法要优于传统遗传算法，行驶里程、缺货损失成本以及变动成本都呈现不同程度的下降，表明变邻域遗传搜索算法可以更好地服务于客户，同时有利于配送中心的长期发展，也验证了该算法在解决车辆配送路径中的可行性和有效性。通过该算法的验证，非冷链商品的配送路径选择时应关注以下要点：一是，面向不同服务对象的地理位置信息及各项服务需求信息时，物流企业若追求利益的最大化，应对模型中的参数不断进行调试，寻找出最优的配送路线；二是，将变邻域遗传算法应用于非冷链运输时要保证一定数量的服务对象，服务对象数量较少时呈现的结果与传统算法相比效果不明显，只有选定较多的服务对象时，效果才能愈加显著。因此，当需求点数量较多时可选择该算法进行研究，既能降低成本也能提高求解速度。

4 结论与展望

本文基于相关文献研究，面向非冷链商品，考虑顾客缺货损失成本，构建了带有顾客服务时间窗口，并以总成本最低为目标的车辆配送路径模型。研究中，将传统遗传算法和变邻域搜索算法相结合形成变邻域遗传搜索算法，能实现利用不同动作构成的邻域结构进行交替搜索操作，在平衡了疏散性与集中性的基础上，形成局部最优解，并将局部最优解进一步作为遗传算子进行交叉变异搜索操作来求取全局最优解。经研究得出如下结论：一是，在面向非冷链商品车辆配送路径的研究中，充分考虑需求点的服务需求与商品的特性，建立起合理有效的优化模型并运行后，结果表明将研究提出的变邻域遗传搜索算法用于非冷链商品配送路径优化，能够有效实现各项成本的最低化；二是，从模型应用视角，本文应用的变邻域遗传搜索算法充分结合了变邻域算法的全局搜索特点及变邻域搜索算法高效的局部搜索能力，该算法较传统遗传算法和变邻域算法而言，既提高了求解精度又提升了求解速度，同时验证了该算法的可行性。

本文探究了面向非冷链商品，以综合成本最小为目标的车辆配送新方法后，考虑到研究对象与研究目标的局限性，认为可继续向具有一定时效性的冷链商品进一步探索，验证变邻域遗传搜索算法的适用性。除此之外，后续还可开展以最短配送时间、最短配送路径等为目标的研究，进一步验证其可行性，为物流行业的发展添砖加瓦。