深度解析以折纸为背景的中考题

冯志贤

(江苏省常熟市白茆中学,江苏 常熟 215532)

例1 已知矩形纸片ABCD,AB=2,AD=1, 将纸片折叠, 使顶点A与边CD上的点E重合.

(2) 如果折痕FG分别与CD、AB交于点F、G,AED的外接圆与直线BC相切, 求折痕FG的长, 如图1[1].

图1 例1题图

折叠方法解析本题的折纸操作方法可以用以下 4 个步骤描述:

操作1 将AD与BC重合对折, 折痕为MN, 如图2所示;

图2 操作1图

操作2 将AD与MN重合对折, 折痕为RS, 如图3所示;

图3 操作2图

操作3 过S、M两点折叠, 折痕为MS, 折叠以后BS与AD的交点为F, 如图 4所示;

再生水是指废污水经适当处理后，达到一定的水质标准，满足某种使用要求，可以进行有益使用的水。本文主要梳理了美国、以色列、新加坡等国（以美国为主）及相关国际组织在再生水利用方面的诸多经验，以期对我国再生水利用提供借鉴。

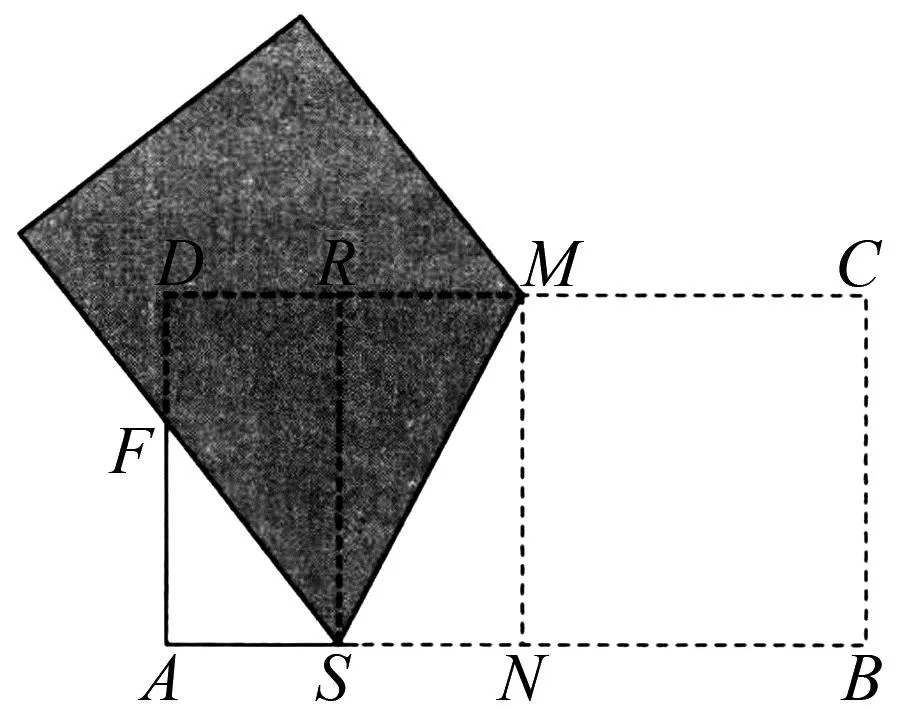
图4 操作3图

操作4 过点F将点A折到CD上, 折痕为FG, 点A的对应点为E, 如图5所示.

图5 操作4图

(2)折叠的关键是要确定点E的位置,我们先假设已经折出来了,如图6所示,然后再计算CE的长度,从而确定点E的位置.

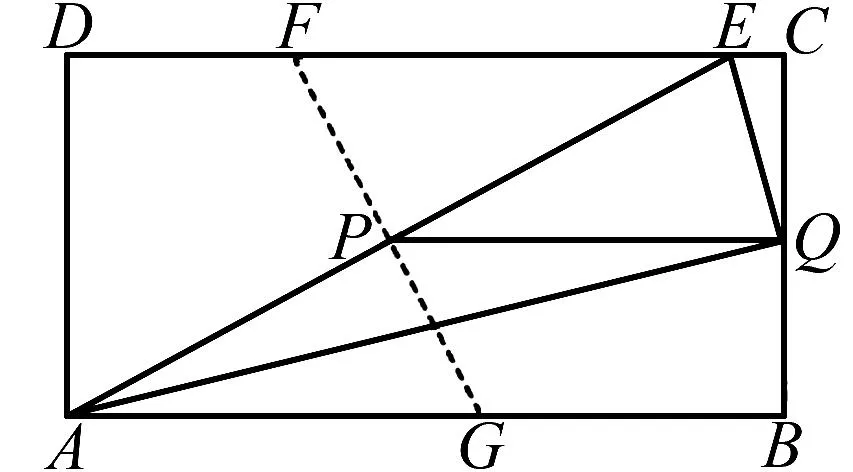
图6 确定E的位置

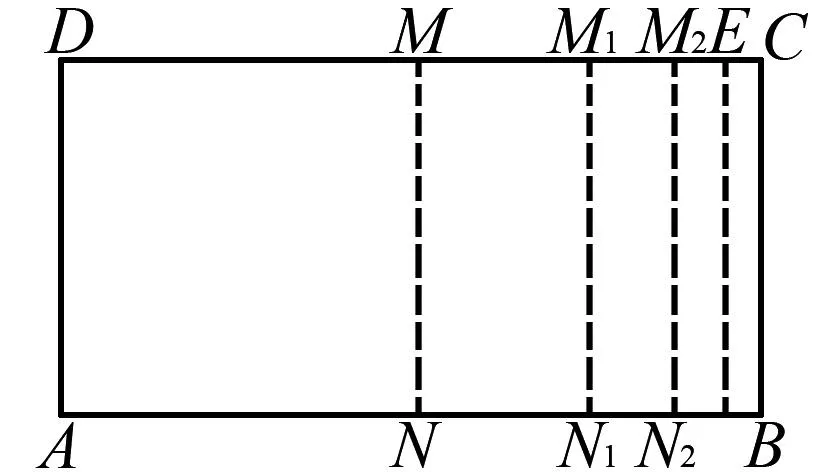
图7 操作5图

操作6将A、E两点重合对折, 折痕为FG, 如图8所示.

图8 操作6图

求折痕FG的长度.

在图8中, 由操作6知GF⊥AE, 所以∠AGP+∠GAP=90°, 而∠GAP+∠DAE=90°, 所以∠AGP=∠DAE.

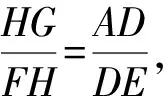
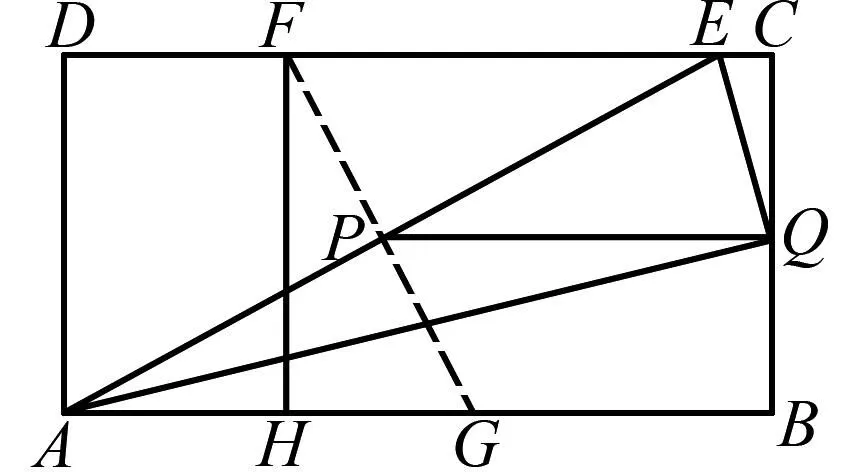
图9 计算FG的长

例2 如图10,在梯形ABCD中,AD∥BC,AB=DC=3,沿对角线BD翻折梯形ABCD,若点A恰好落在下底BC的中点E处,则梯形的周长为____.

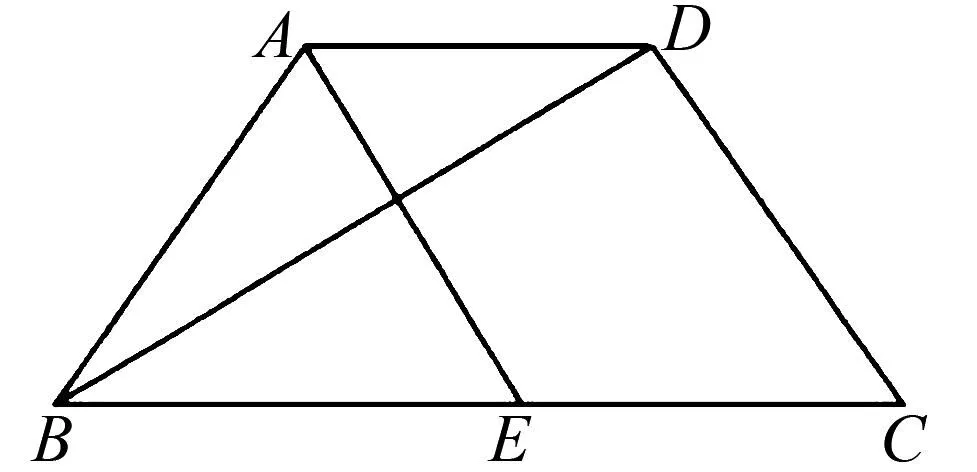
图10 例2题图

折叠方法解析“沿对角线BD翻折梯形ABCD”,实际上是过B、D两点折叠;“若点A恰好落在BC的中点E处”这必须是非常特殊的梯形才能办到.那么这是怎样的一个梯形呢?

如图11所示,因为点A关于折痕BD的对应点为E, 所以△ABD≅△BDE, 即AB=BE,AD=DE,∠ADB=∠EDB.因为AD∥BC,有∠ADB=∠DBE,所以∠DBE=∠EDB,即BE=DE,因此四边形ABED是菱形.又因为E是BC的中点,而AB=CD,所以△CDE是等边三角形.

图11 折叠解析

问题解答由上述讨论可知, 梯形ABCD是底角为60°的等腰梯形,周长等于5倍腰的长度,即等于15.

例3 矩形纸片ABCD的边长AB=4,AD=2, 将矩形纸片沿EF折叠, 点A与点C重合, 折叠后在其一面着色 (如图12), 则着色部分的面积为( )[2].

折叠方法解析“将矩形纸片沿EF折叠,点A与点C重合”,实际上,将两点重合对折的折痕是唯一的, 所以先给出折痕,然后再将两点重合对折这种描述方式不够严谨,本题的操作过程可以描述为:将矩形ABCD的两顶点A与C重合对折,折痕为EF,点D的对应点为G,如图13所示.

图12 折叠解析

问题解答求梯形CEFG的面积.

因为点A关于折痕EF的对称点为C,点D关于折痕EF的对应点为G,所以四边形ADFE与四边形CEFG全等,所以AD=CG,又因为折痕垂直平分两对应点的连线,即EF垂直平分AC,有CF=CE,所以梯形CEFG的上底FG加下底CE正好等于CD,于是梯形CEFG的面积等于4.

例4 如图14,矩形ABCD沿AE折叠,使点D落在边BC上的点F处,如果∠BAF=60°, 那么∠DAE=( )[3].

A.15° B.30° C.45° D.60°

图13 例3题图

折叠方法解析可以将“矩形ABCD沿AE折叠,使点D落在边BC上的点F处”描述: 过点A将点D折到BC上,折痕为AE,D的对应点为F, 如图14所示.

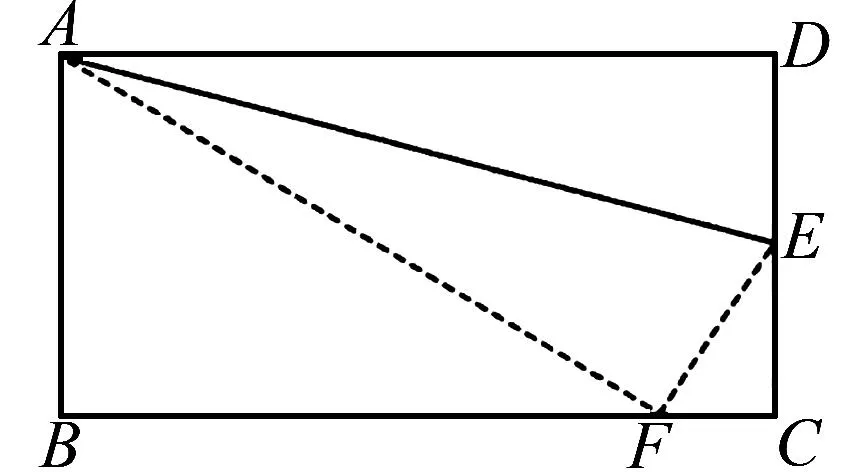
图14 折叠解析

问题解答从条件∠BAF=60°可知, 且∠DAE=∠FAE, 即∠DAE=15°.

纵观以上的考题,我们发现很多的中考题都是以折纸为背景来考查的,这就要求一线教师在日常教学中要渗透折纸艺术、关注学生的动手操作能力.同时,也在教学中启示了一线教师:折纸可以进入中小学数学课堂,通过折纸操作活动,引导学生观察折痕所形成的边角关系,帮助学生建立折纸操作与数学内容的联系,培养其动手能力、观察能力、想象能力和创造性思维能力.还要注意科学性与操作性相结合、趣味性与严谨性相结合、启发性与示范性相结合的原则.