猜想归纳方法在初中数学学习中的应用策略
2024-01-11王海珠
王海珠
(民乐县初级实验中学,甘肃 张掖 734500)
猜想归纳法是在初中数学学习中常用的方法,它可以帮助学生从单个例子中得出普遍规律[1].通过猜想归纳法,学生可以从具体的实例中获取信息,并推断出潜在的数学规律,这样,他们就能够逐步地建立数学概念和知识.在数学学习中,掌握猜想归纳法是非常重要的,因为它可以培养学生的逻辑思维和分析能力,帮助他们更好地理解数学概念,提高解决问题的能力.本文旨在介绍如何在初中数学教学中有效地应用猜想归纳法,以便帮助学生掌握这一重要的数学思维工具.
1 数式规律中的猜想与归纳
数式规律的猜想归纳方法是数学学习中的重要思维方式.一般来讲,数式规律的猜想和归纳分为3个步骤:观察给定数字或运算式子的特点与规律;做出猜想,并通过若干个例子进行验证;通过对现象的归纳总结,描述规律的特征或者写出表达式.
通过观察和猜想,学生可以主动探索数学规律,培养他们的逻辑思维和问题解决能力.通过多个例子进行验证,并通过归纳总结,学生可以形成准确的规律描述,提高他们对数学概念的理解和运用能力.这种积极主动的学习方式,有助于学生自信地面对数学问题,并培养他们的数学兴趣.
例1 观察下面各式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
(x-1)(x4+x3+x2+x+1)=x5-1,…;
据此规律, 求 22 023+22 022+22021+…22+2+1 的个位数字是 ( ).
A. 1 B. 3 C. 5 D. 7
解析首先,观察题目中的规律可知: (2-1)(22 023+22 022+22 021+…22+2+1)=22 024-1,接着,进行猜想,2n是由n个2相乘得到,因此,其个位数字可能有一定的规律,然后进行举例验证,得到:21=2,22=4,23=8,24=16,25=32,26=64,…,因此验证得到其个位数字按照每4个进行1次循环.因为2 024÷4=506,所以22 024的个位数字是6,22 024-1的个位数字是5.
点评本题中,根据题目的设问,进行大胆猜想是解题的关键.按照3个步骤严格执行,可以大大提升解题正确率.由于22 024是一个极大的数字,因此一定有规律可循,所以在第2步的猜想中,常规步骤为先猜想后验证,但若无思路,可先举例再总结,也不失为一种巧妙的方式.可见在数学学习中,不能“眼高手低”,多动笔多尝试才是正确的解题方式.
2 图形变换中的猜想与归纳
图形变换规律可以帮助学生培养观察、思考和解决问题的能力.在图形规律的学习过程中,学生需要通过观察给定的图形,发现其中的规律和特点;尝试自己添加辅助线,通过不断尝试探索出规律;最终,学生需要用数学符号和语言来准确地阐述图形规律,并通过实例来验证.
图形变换规律的学习可以培养学生的创新思维和问题解决能力.通过观察和猜想,学生可以自主探索图形规律,并提出自己的策略和想法,进一步提高他们的抽象思维能力.此外,图形规律的学习也有利于学生了解和掌握各种数学概念和方法,为他们日后的学习打下坚实的基础.
例2 如图1所示,矩形ABCD的面积为20 cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1,以AB,AO1为邻边作平行四边形AO1C2B……依此类推,则平行四边形AO2 022C2 023B的面积为( ).

图1 图形变换规律
解析因为四边形ABCD是矩形,所以AO=CO,BO=DO,DC∥AB,DC=AB,所以:
…………

点评本题的解题关键在于找到图形每次“变换”后的规律.这道题的规律和特点较为明显,即每次得到的平行四边形,都是从上一个平行四边形的“中心”引平行线,因此,在底边长度不变的情况下,每次得到的平行四边形面积都为上一个平行四边形面积的一半.如直接观察不易察觉,则可自行添加一个平行四边形的辅助线进行规律的“体验”.
3 周长面积中的猜想与归纳
在学习周长面积规律时,学生需要关注图形的数量、形状和组合方式等特征,进而发现并做出周长或面积相关规律的猜想.最终,通过归纳和总结,学生能够得到周长或面积之间的关系,并编写公式以便计算.周长面积规律的学习有助于学生理解图形的属性,通过观察和实践,学生能够深入理解图形周长或面积的规律,同时也能够应用所学的知识进行问题解决和计算.
例3 如图2所示,在△ABC中,点E是AB边上的点,且AE:EB=2:3,点D是BC边上的点,且BD:DC=1:2,AD与CE相交于点F,若四边形BDFE的面积是16,则△ABC的面积为( ).

图2 三角形内部分割
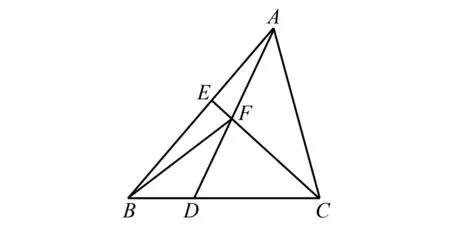
图3 添加辅助线
解析连接FB, 如图3所示:

点评本题以面积的规律为例,通过三角形“等高”时,面积比等于底边长度比,得到面积的一般规律,进而将其转化为代数式进行求解.该类猜想归纳与前述找规律类的猜想归纳有些差异,该类猜想归纳是围绕“特定条件或者性质”进行的推理,并将推理所得的表达式进行求和或者变形.其中,推理是猜想,求和或变形是归纳,在数学学习中,该类猜想归纳的技巧需要掌握.
4 点的坐标规律中的猜想与归纳
在学习点的坐标规律时,学生需要观察图形上点的坐标变化规律,特别是注意横纵坐标之间的关系,进而做出猜想并通过实例进行验证.比如,移动图形、增加点数量、改变图形形状等.最终,通过归纳和总结,学生能够得到点的坐标规律,并编写公式以便进行计算.点的坐标规律的学习有助于培养学生的观察力.通过观察和实践,学生能够发现和理解点在平面上的位置变化规律,并通过归纳总结建立起数学模型.掌握点的坐标规律,不仅对于几何学和代数学的学习具有重要作用[2],还可以应用于实际问题的解决,如地理测量、航空航天等领域.
例4 如图4所示,在平面直角坐标系中,四边形ABCD是平行四边形,A(-1,3)、B(1,1)、C(5,1).规定“把平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2 023次变换后,平行四边形ABCD的顶点D2 023的坐标变为( ).
A.(-2 019,-3) B.(-2 019,3)
C.(-2 020,3) D.(-2 020,-3).
解析由于四边形ABCD是平行四边形,A(-1,3)、B(1,1)、C(5,1),所以D(3,3),把平行四边形ABCD先沿x轴翻折,再向左平移1个单位后,得到D1(2,-3),观察,发现规律:D0(3,3),D1(2,-3),D2(1,3),D3(0,-3),D4(-1,3),所以对于横坐标,每次变换减1,对于纵坐标,奇数次变换为-3,偶数次变换为3,经过2 023次变换后,D2 023(-2 020,-3).

图4 平行四边形
点评本题考查翻折变换、点坐标的规律性.先利用平行四边形的性质求出点D的坐标,再将前几次变换后Di(i=1,2,3,…)点的坐标求出来,观察规律即可求解.解题的关键是先求出D的坐标,再利用变换的规律求解,在求解的过程中,列举实例依然是最佳的找规律的手段,由此可见,数学的学习过程并不是仅靠天赋,更多还是要依靠勤于动笔.