一道2021年奥林匹克竞赛试题的多解探究与推广

贵州师范大学数学科学学院 (550025) 徐凤旺 成 敏 尹正波

1 试题呈现

这是2021年摩尔多瓦奥林匹克竞赛试题的一道求函数最小值问题,可以看出该试题的条件式子和结论结构对称,具有数学的美感.本文拟对该试题的求解方法、变式及推广做进一步的探究,与大家一起分享.

2 试题解析

评注:此解法通过构造函数f(x),结合函数的凹凸性与琴生不等式,求得该函数的最小值.

评注:此解法通过构造函数,利用函数切线的性质,求得该函数的最小值.

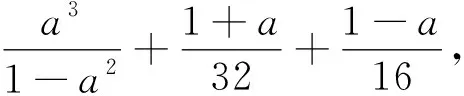
3 试题变式

分析:此变式是通过改变未知数的“幂”得到,将分子和分母的未知数的幂从“3”和“2”变为“2”和“3”.

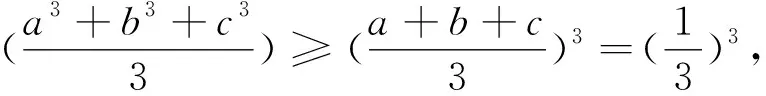
分析:此变式是2022年马其顿的数学奥林匹克竞赛试题,将2021年摩尔多瓦奥林匹克竞赛试题条件式子中的“1”变为“3”,每一项分母的未知数的系数“-1”变为“+1”得到.

分析:此变式是通过把每一项分子的未知数的幂从“3”变为“2”得到的.

分析:此变式是通过改变每一项分母的结构得到的,将分母的项数从“2”项变到“3”项.

4 试题推广

分析:此推广是在变式1的基础上将每一项分母的系数“1,-1”推广到“λ,-μ”,未知数的个数从“3”元推广到“n”元.

分析:此推广是在变式2的基础上将每一项分母的系数“1,1”推广到“λ,μ”,未知数的个数从“3”元推广到“n”元.

分析:此推广是在变式3的基础上将每一项分母的系数“1,-1”推广到“λ,-μ”,未知数的个数从“3”元推广到“n”元.

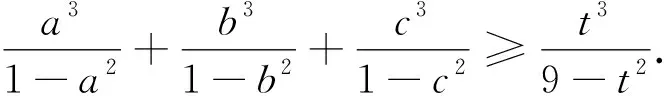
分析:此推广是将试题中条件式子的结果从“1”推广到“t”.

分析:此推广是在推广4的基础上将每一项中分母所含的常数项“1”推广到“λ”.

分析:此推广是在推广5的基础上将每一项分母所含的未知数的系数“1”推广到“μ”.

分析:此推广是在推广6的基础上将未知数的个数从“3”元推广到“4”元.

分析:此推广是在推广7的基础上将未知数的个数从“4”元推广到“n”元.

分析:此推广是在推广8的基础上将每一项分母和分子的未知数的幂从“2,3”推广到“2k,2k+1”.

上述推广1到推广3的证明过程与对应的变式1到变式3的证明思路是类似的,推广4到推广8均是推广9的特例,证明思路也是类似的,这里给出推广9的证明,其余推广的证明不再叙述.