另解一道调研测试压轴题
2024-01-09湖北省武汉市第二中学430010
中学数学研究(江西) 2024年1期
湖北省武汉市第二中学 (430010) 张 鹄
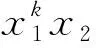
试题以考生熟悉的含参的函数方程零点问题为情境进行设计.第一问主要考查已知函数零点个数求参数a的取值范围;第二问以题干中两个零点组合表达式存在具体最值为条件求解参数k的值.两问由易到难,层层递进,能较好的考查学生的函数与导数等方面的数学核心素养与关键能力.为了有效发掘试题内涵,积极引导后期复习备考,本文给出我们的若干方法,不当之处,恳请指正.
第(1)问采用分类讨论的方法,解法较为基础,方法如下:

以下重点讨论第(2)问的解法.

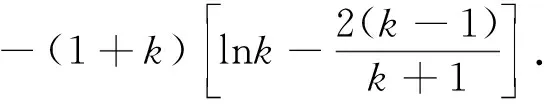
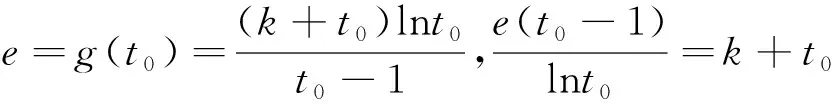
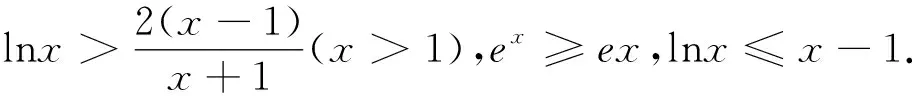

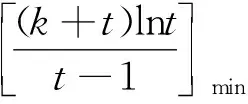
以上三种解法中,方法1运用分类讨论方法,对含参数的函数存在最值展开研究,不断地对问题进行转化,构造多个函数模型进行分析;方法2抓住函数取极值点处的函数性态并结合极值存在的必要条件与充分条件入手做出分析;方法3灵活运用分离参数方法将原问题转化为不等式恒成立问题且存在取等临界情形.通过对试题解法的深入分析,一方面加深了考生对此类函数与导数问题的理解,另一方面也明确了后期数学复习备考的方向.
