探究三类用量词表述的参数范围问题
2024-01-09安徽省天长中学239300叶士儒
安徽省天长中学 (239300) 叶士儒
在数学用语中所称的量词就是“存在量词”与“全称量词”两种形式,如果在一个数学问题中含有存在与任意的字眼,我们必须对此种命题有正确的理解,并需要及时的将此类数学问题转化为我们熟悉的题目类型,这样才能迅速地切入问题的实质,为能成功解题铺垫好坚实的基础.导数法是解决函数中若干问题的重要方法,尤其在解决有关参数范围问题中效果非常突出.本文通过举例分析和点评,介绍导数题中三类常见的用量词表述的参数范围问题的求解策略,以探求解题思路、揭示解题要点为目的,希望能给朋友们带来一些启发.
一、同种形式量词的不等问题
在一个题中含有两个存在量词或两个全称量词,他们所表示含义是不一样的,需要正确理解其实质,将其转化为我们熟悉的代数问题.

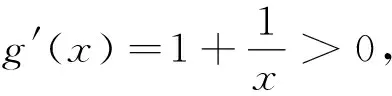
点评:题中含有两个存在量词,即若存在x1,x2∈[1,e],使得f(x1) 点评:本题是含有两个所有量词类型题目,它的实质是恒成立问题,通过将问题转化变成一个恒不等式,然后再进行分离参数处理,转化为求另外一个新函数的求最值问题,这就是我们熟悉的题型了. 在一个问题中若含有两类量词的表述,常规是有两个变量,其中一个受到另一个的影响,一般都是可以转化为求两个同类最值问题. 点评:在本题中出现的是先任意,后存在的两种量词,由于用“≤”连接,则可转化两个最大值的不等关系,通过求最大值再解不等式就使问题获解. 点评:本题与例3的条件类似,只是给出的不等式是用“≥”连接,但是意义也不同,此处是转化为两个函数求最小值,然后利用不等关系解决问题. 对于两个函数中,可能出现其函数值相等的情况,而用不同量词表述的其实质也是有区别的,解题时需要认真分辨,理解清楚. 点评:此题是存在两个函数值相同问题,所以只需分别求出两个函数的值域,再找出让这两个值域有交集时,满足条件的参数取值范围就出来了. 点评:此题是两个函数值等式恒成立问题,可翻译成其中一个函数的值域是另一个函数值域的子集,也就将问题转化为求两个函数值域问题.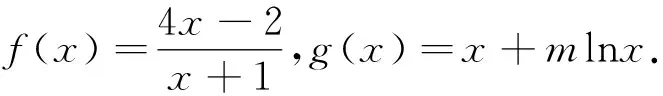
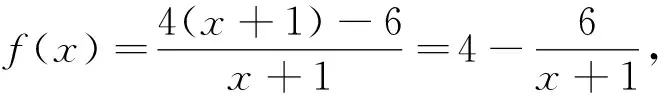
二 不同形式量词的不等问题
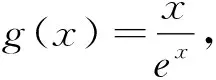
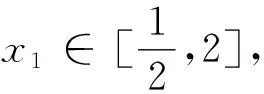


三 两个量词的相等问题