一道IMO选拔赛不等式题的推广
2024-01-09浙江省江山中学324100
中学数学研究(江西) 2024年1期
浙江省江山中学 (324100) 王 芳
题目(2022年印度尼西亚IMO选拔赛)已知正数a,b,c满足abc=1,求证:(a+b+c)(ab+bc+ca)+3≥4(a+b+c).(1)
不等式(1)的两边都含有相同的因式(a+b+c),只要将不同的因式(ab+bc+ca)进行放缩,即可获证.
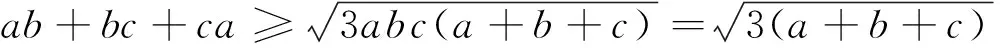
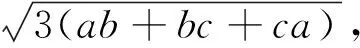
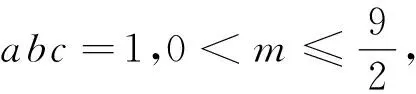

有了推广1,我们考虑在不等式(3)中相同的因式(a+b+c)之中进行添项处理,结果得到如下:
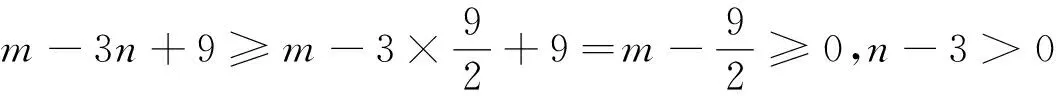
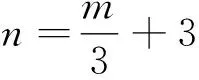
推广3已知正数a,b,c满足abc=1,求证:
(1)当k≥1时,(a+kb)(b+kc)(c+ka)≥4k(a+b+c)+k3+3k2-9k+1;(9)
(2)当0 证明:由于(a+kb)(b+kc)(c+ka)=k3+1+k(a2b+b2c+c2a)+k2(ab2+bc2+ca2),因此,当k≥1时,(a+kb)(b+kc)(c+ka)=k3+1+k(a2b+b2c+c2a+ab2+bc2+ca2)+k(k-1)(ab2+bc2+ca2)≥k3+1+k[(a+b+c)(ab+bc+ca)-3]+3k(k-1)≥k3+1+k[4(a+b+c)-3-3]+3k(k-1)=4k(a+b+c)+k3+3k2-9k+1,即不等式(9)成立.当0
