解三角形中取值范围问题的解法探究与思考

福建省福清融城中学 (350300) 王 强

解三角形问题一直是高考的高频考点,在解三角形的背景下,若已知的方程个数比未知的边角元素个数少,就会变成不确定三角形,对于不确定三角形,我们常研究最值及范围问题,这类问题注重与函数、不等式和几何等知识的交汇融合,涉及的知识面广,灵活性大,综合性强.本文结合典型例题,对解三角形中的取值范围与最值问题的破解策略与路径做一梳理与归纳,与同仁交流.

1 试题再现

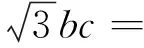
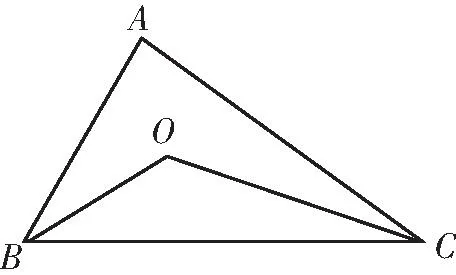
图1

2 问题剖析

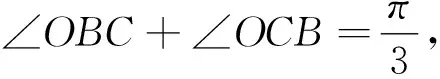
3 解法探究

3.1 统一解析

为了叙述方便,对所用主要知识做统一解析:

3.2 多解探究

探究1遵循函数思想,利用正弦定理,化边为角,转化为三角函数的值域问题.

探究2借助图形观察分析,利用数形结合思想,找临界位置,此时△ABC为直角三角形.

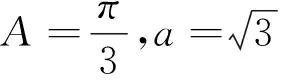
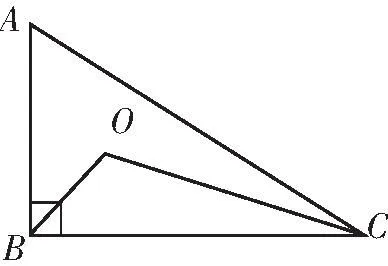
图2

4 策略剖析

解法一更具一般意义,是解决此类问题的通法. 本题是解三角形中的有关最值(取值范围)问题,当条件不够时,需引入一个新的变量,构造出待求最值关于这个变量的函数．这样,由于变量的引入,使得我们具备了运用通法“知三求三”解决问题的条件,进而用通法将问题予以解决．其中“函数思想”就发挥了重要作用,用运动变化的观点,分析问题中的数量关系来建立函数,可以以边为变量,也可以以角为变量．

剖解法特征,探破解策略.此类问题的解题路径为:

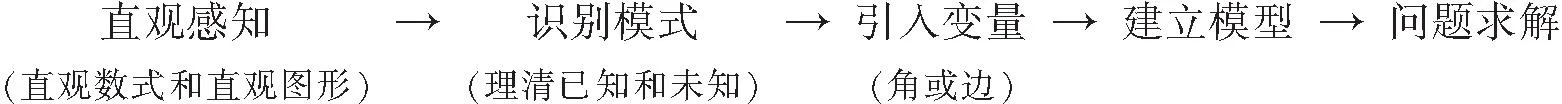
5 应用赏析

以上两个不同角度的探究,从基础知识入手,运用代数方法和几何方法,通过合理转化,选择恰当的方法,找到解决此类问题的一般方法,显然函数思想更具一般性与普适性.

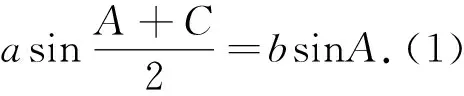
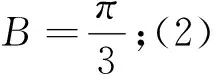
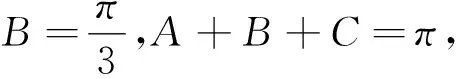
分析:本题仅知一边及其对角,显然这是一类不确定三角形的求解问题,注意到本题是最值问题,若能立意与函数思想,则自然就能运用通法将问题解决;当然若能基于不等式思想,结合余弦定理,寻找和、积、平方和、倒数和这些结构之间的关系,也是求解三角形最值的重要方法之一.

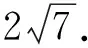
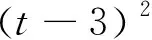
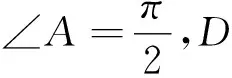
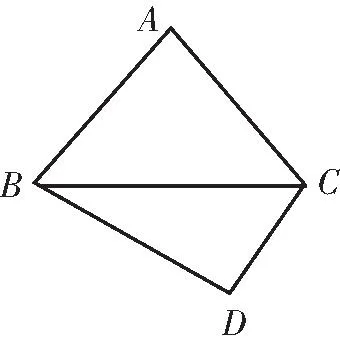
图3

6.解后反思

我们常说,教学应以学生为主体,那么如何在解三角形的教学中体现学生的主体地位?笔者认为教师最基本应该做到,引导学生会用数学眼光去观察问题,即数学抽象,由数量关系或图形去识别解三角模式,抽象出一般规律和结构,巧妙转化,掌握化归转化思想,培养数学抽象和直观想象素养;同时还要引导学生会用数学思维去思考问题,即逻辑推理,合理引入变量,建立函数模型,求得正确的运算结果,掌握函数方程思想,培养逻辑推理和数学运算素养．