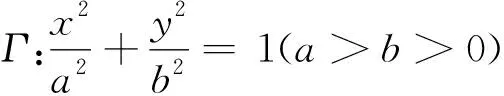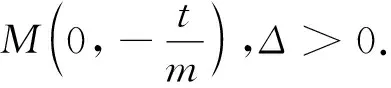一道“非对称性”问题的解法优化与拓展
2024-01-09安徽省合肥市合肥一六八中学230601吴志勇
中学数学研究(江西) 2024年1期
安徽省合肥市合肥一六八中学 (230601) 张 倩 吴志勇
圆锥曲线中极点和极线的理论为我们求有关定点、定值部分问题提供了大的方向,而韦达定理的使用往往使方向的正确性得到了严谨的证明.但在实际的解题中我们经常会遇到仅仅套用韦达定理不能一次性解决的“非对称性”问题.本文以对一道试题解法进行优化处理为例,借此来谈谈对解决有关圆锥曲线中“非对称性”问题的想法.
1 原题及求解
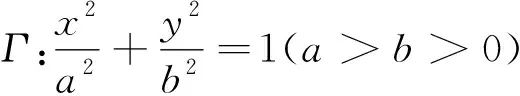
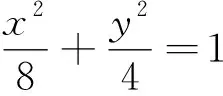
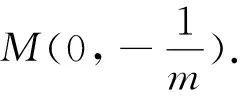
2 思路探求
探求一:利用椭圆第二定义将“非对称性”转化为“对称性”

探求二:利用韦达定理部分消元
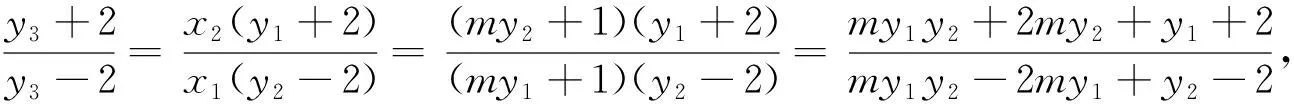
探求三:和积转换代入化简
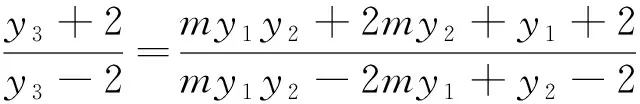
3 方法与应用
综合原题的解法和笔者的探求,可以将解决韦达定理应用中与“非对称性”有关的方法总结为以下四种:⑴分析结构,平方消元;⑵利用圆锥曲线第二定义将“非对称性”问题转化为“对称性”问题;⑶利用韦达定理部分消元;⑷和积转换代入化简.以下笔者分别用方法四解决一道与双曲线有关的问题来弥补“探究三”的不完整性和方法二来证明一个一般性结论作为本文的收尾.
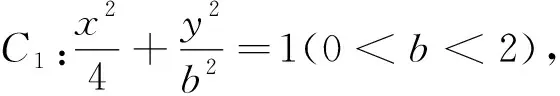

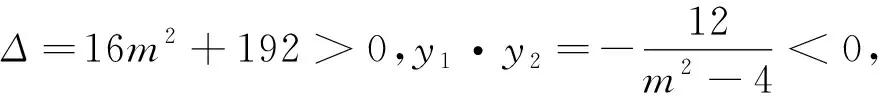
本题也可以采用其他的三种方法得出结论,但相对于本题的情况采用和积转化法相对来说是比较简洁的.故我们在平时的教学中,要引导学生熟练掌握四种不同的方法,根据具体的情况,灵活运用.最后我们来运用方法二证明一个一般性结论.