变式练习在初中数学教学中的应用策略研究
2024-01-08莫兴展
莫兴展
【摘要】变式练习是一种常规的数学教学方法,在素质教育背景下被广泛应用,它通过指导学生参与变式练习的方式组织初中数学教学活动,能帮助学生在解题过程中探寻知识规律,发展思维能力,逐渐构建完善的知识体系.为了更好地实现理想化的教育目标,文章在分析变式练习在初中数学教学中的应用意义的基础上,提出教师可以通过精心设计变式题组、构建生活情境、指导合作学习、引导全员参与等方式组织变式练习,为学生创设开放、自主的学习环境,促进学生的全面发展.
【关键词】变式练习;初中数学;应用策略
目前,部分学生在初中数学学习阶段经常出现理解某一问题,但对此类题型缺乏系统性理解的现象.产生这种现象的原因是学生并未理解知识的精髓与本质,从而导致无法灵活运用.为解决这一问题,发展学生的思维能力,教师需要积极探寻变式练习在初中数学教学中的意义,然后根據学生的实际学习情况与教学主题为学生提供丰富的练习资源,指导学生通过已有知识经验发散数学思维,提高核心素养,从而推动初中数学教育改革的发展.
一、变式练习在初中数学教学中的应用意义
变式练习就是从不同的角度改变已有的数学素材或问题的呈现方式,进而突出知识的本质特征.变式既是一种思想方法,也是创新的重要途径.变式练习包含解法变式和题目变式,将其运用于初中数学教学具有重要意义.第一,采用变式练习的方式,教师可以根据习题中蕴含的数学知识为学生提供与之相关的平行训练,鼓励学生从不同视角对问题进行分析,再利用所学知识解决问题.久而久之,学生会对知识产生更加全面的理解,并通过层层递进的变式推动思维的螺旋上升.第二,新课改倡导培育学生的核心素养,而在变式练习中,学生能逐渐摆脱对教师的依赖,结合教师提出的问题探究其中蕴含的本质特征,逐渐构建知识框架,发展自身思维能力,最终实现核心素养的发展,在深度学习中增进思维的灵活性与创新性.第三,借助变式练习,教师可以围绕教学目标与教学难点设计巩固练习,在题目训练中发现学生存在的普遍问题,从而深化对变式理论依据的理解,更好地掌握数学教学的基本方法,促进自身专业能力与专业素养的提高.
二、变式练习在初中数学教学中的应用要点
在组织变式练习的过程中,教师不能直接提供变式题目让学生进行练习,而需要从多角度出发考虑变式练习的适用性,这样才能保障教学活动得以顺利进行.为此,笔者对变式练习中需要关注的要点进行了总结:第一,变式练习的合理使用能帮助学生更好地掌握学科知识,发展核心素养,但任何事物都具有两面性,如果应用不当则可能影响学生的学习积极性,导致学生产生严重的心理负担.因此,在变式练习的内容设计方面,教师需要兼顾学生学习能力,把握好变式的“量”和“度”,确保变式练习内容与学生最近发展区相吻合,难度适中,不会给学生造成较大的心理负担.第二,营造积极民主的课堂活动氛围很关键.教师需要充分发挥自身引导作用,结合学生的实际学习情况,巧妙运用语言引导的方式积极与学生进行沟通、交流,拉近师生之间的距离,消除学生对教师的恐惧感,使得学生在和谐平等的课堂中增强情感体验,愿意参与教师设计的变式练习.第三,变式练习的形式多种多样,教师在设计的过程中需要结合知识点以及题型进行综合考虑,以服务本节课教学目标为目的,注重数学思想与数学方法的渗透,避免变式练习出现功利趋向,确保学生能在思考中了解开展变式练习的真正目的.
三、变式练习在初中数学教学中的应用策略
变式练习是一项长期工作,教师需要做好“打持久战”的准备,充分发挥变式练习的潜在价值,激发学生的潜能.下面笔者将对变式练习的具体应用策略进行总结,以供广大教师参考借鉴.
(一)围绕核心素养,精心设计变式题组
核心素养是教育改革背景下的重点培育目标.在变式练习设计中,教师不仅要兼顾本课重点知识,而且要以核心素养为目标,借助变式练习发展学生的核心素养.因此,在课前准备阶段,教师应深入研读教材,基于核心素养设计变式题组,为后续教学活动的顺利进行奠定基础.
以“整式的乘法”一课为例,本课教学目标是使学生经历探索整式乘法运算法则的过程,掌握乘法运算的算理,发展运算能力,并体会乘法分配律的作用与转化思想.在本课中,教师可以“抽象能力”“推理意识”这两点展开设计练习.首先,围绕学生的数学抽象素养,教师可以借助生动的直观感知为学生提供理解的起点,引导学生思考:如图1是一个长和宽分别为m,n的长方形纸片,如果它的长和宽分别增加a,b,则所得长方形(如图2)的面积应该如何表示?教师可指导学生利用整式乘法与因式分解知识分析问题,引导学生类比数的运算,以运算律为基础得到整式乘法运算与因式分解之间的关系.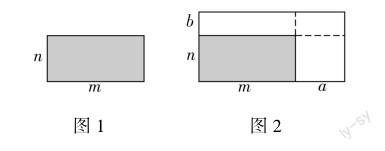
在此基础上,教师可以设计与之相关的变式练习:为了扩大小区的绿地面积,现将其中一块长xm、宽ym的长方形绿地的长和宽分别增加am和bm,你能用几种方法表示扩大后绿地的面积?不同的表示方法之间又有什么关系?
教师借助变式练习的方式帮助学生从单项式乘单项式迁移到多项式乘多项式问题中,发展了学生的抽象能力与推理意识,使得学生能更好地掌握整式乘法知识.
设计说明:教师借助图形问题设计整式乘法计算问题能培养学生的数形结合思想,帮助学生在解决问题中生成核心素养,有效的变式题组设计还可以提升教学质量,确保学生能积极参与其中,并获得深层次发展.
(二)构建生活情境,激发学生练习热情
对学生而言,枯燥的学习方式难以激起其学习积极性,因此,教师需要以培养学生学习兴趣为目的设计变式练习.为确保学生顺利达成知识的迁移与运用目标,教师可以建立学科知识与生活的联系,借助情境创设的方式将数学变式练习转化为与生活息息相关的内容,帮助学生在练习中体会数学的重要价值,提高对数学学习的重视程度.
以“求解一元一次方程”一课为例,在学生已经掌握一元一次方程的基本内涵后,教师需要指导学生利用所学知识解决实际问题,发展学生的运算能力,帮助学生了解一元一次方程在具体事件中的使用方法.结合本课重点内容,教师可为学生设计以下练习题目.
练习1 某服装店搞促销活动,已知老板将一件冲锋衣按照成本价格提高40%后标价,又以八折的优惠方式卖出,经过计算,这种售卖方式仍能保障每件衣服获利15元,请计算每件冲锋衣的成本价格是多少元.
变式1 小明在某公园售票处工作.一天结束后,他共售出了1000张票,已知公园的成人票价与学生票价分别为8元和5元,总票款为6950元,请帮助小明计算今日所售出的成人票与学生票各有多少张.
变式2 小刚家距离学校1000m,小刚以80m/min的速度前进,5min后,妹妹以180m/min的速度骑车追赶小刚,并且在中途追上了他.求妹妹追上小刚花费了多长时间,以及在追上小刚后距离学校还有多远.
(三)指导合作学习,培养学生发散思维
合作学习是教育改革背景下大力倡导的一种新型学习方法.教师通过指导学生参与合作学习能帮助学生通过集中讨论的方式解决问题,同时培养良好的合作能力.因此,在指导学生参与变式练习的过程中,教师同样可以沿用合作学习的方式,为学生提供变式练习,并鼓励其在交流中给出不同的解决方法,从而积累学习经验,形成一题多解的能力.
一题多解就是教师启发、引导学生对同一个数学问题从不同的角度、不同的解题思路、用不同的数学方法去解答.以“三角形的中位线”一课为例,结合本课重点内容,教师可基于学生学习表现合理划分小组,并为学生提供这样一个问题:如图4,在△ABC,△ADE中,∠BCA=∠DEA=90°,A,C,E在一条直线上,且BC=DE,连接BD,M,N分别为AB,CE的中点,连接MN.求证:AD=2MN.
根据教师提供的内容,各组成员积极参与讨论,利用所学知识解决问题.在学生讨论中,教师要有意识地指导学生从多种解法中找到适合自己的方法,然后在班级中进行分享,交流解法.
(四)引导全员参与,提升学生创新能力
变式练习的目的是帮助学生在以不变应万变的过程中掌握数学知识,牢记基础理论.因此,为提高学生的参与度,教师可以在为学生提供变式练习的基础上,指导学生根据理论知识自主改变题目中的表述方法,设计变式练习,在班级中分享自己的题目并邀请其他同学回答.这样既能有效增强学生的情感体验,又能帮助学生更好地发展创新能力,掌握变式的精髓,逐步提高学习能力.
以“用配方法求解一元二次方程”一课为例,在本课教学中,教师可带领学生整理解一元二次方程时应先将方程转化为(x+m)2=n的形式,再将两边同时开方转化为求解一元一次方程.在基础教学结束后,教师为学生设计问题“解方程x2+8x-9=0”,指导学生利用配方法解决问题.接下来,为培养学生的创新能力,教师邀请学生尝试围绕配方法的基本法则自主设计问题并在班级中分享,由此深化学生对配方法解一元二次方程的了解.如下为学生自主设计的变式练习.
变式1 解方程:x2-10x+25=7.
變式2 健美操队伍有8行12列,后增加了69人,使得队伍增加的行、列数相同,求增加了多少行和多少列.
变式3 一群猴子分两队,高高兴兴玩游戏,八分之一再平方,蹦蹦跳跳树林里,其余十二叽喳喳,伶俐活泼又调皮,两队猴子在一起,总数共多少只?
设计说明:指导学生尝试自主设计变式练习的方式可以充分调动学生参与学习的积极性,在分析、实践中深化对理论知识的理解,最终养成良好的学习习惯,为后续参与高中阶段数学学习奠定坚实的基础.
结 语
综上所述,在教育改革背景下,优化初中数学教学方法、发展学生核心素养已经成为广大教师关心的焦点问题.在具体教学中,教师可以利用变式练习的方式指导学生学习数学知识.在更具自主性的课堂中,学生能完全地沉浸其中,感受数学的魅力,逐渐掌握基本的学习方法与解决问题的技巧,最终达成理想化的学习目标,形成完整的知识体系.
【参考文献】
[1]周新娣.精彩变换放飞思想:浅谈初中数学变式练习[J].现代中学生(初中版),2022(16):31-32.
[2]张兰.初中数学变式练习的设计策略[J].数理天地(初中版),2022(10):36-38.
[3]晏南飞.初中生提升数学运算能力的策略分析[J].现代中学生(初中版),2022(4):13-14.
[4]简相国.初中数学问题导向型微课的设计与开发[J].新课程研究,2021(23):45-46.
