逆向思维在初中数学解题教学中的应用探究

2024-01-07陈若冰

数学学习与研究 2023年23期

陈若冰

【摘要】初中数学教师在解题教学过程中开展逆向思维培养活动，引导学生运用逆向思维解答各类数学问题，不仅可以开拓其数学解题的思路，提升他们问题解答的效率，还能借此使学生掌握正向解题、逆向解题两种方式，使其能够快速简化问题的解析难度，进而提高其自主解答数学问题的能力.对此，为了使逆向思维解题教学发挥出更好的效果，文章从思维培养视角出发，阐述教师通过开展逆向引导、逆向推论、逆向求解等解题活动，提高学生思维应用能力的具体策略.

【关键词】初中数学；逆向思维；解题教学

引言

在数学核心素养背景下，教师不仅要让学生扎实掌握学科理论知识和数学解题技能，还要培养他们会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界的能力.基于此，在数学解题课程中，教师若想进一步提高学生的解题能力，需要拓展他们的解题思路，通过有效的教学手段启发他们的逆向思维，引导他们运用逆向思维方式理解数学问题，获得新的解题思路，找到有别于以往模式化解题方法的问题解决办法，从而提升其问题解决的效率，提高学生的逆向思维能力.

一、逆向思维的概述

（一）逆向思維的概念

逆向思维是相对于正向思维而言的，是对正向思维进行反方向拓展，也被称之为求异思维，具体指的是从反方向角度出发思考问题、研究问题和解决问题的一种逆向思维方式.学生在使用逆向思维时，能够突破传统思维的束缚，从与众不同的角度出发，对问题进行反方向探究，从而总结出区别于以往模式化解决方法的全新方案.在数学课程中，逆向思维通常应用于解题教学之中，学生需要从数学求解问题反推回已知条件，通过反方向思考数学知识，使问题变得更加简单化，从而快速得出数学问题的答案.

（二）逆向思维的特征

逆向思维具有普遍性、新颖性、批判性三个主要特征.普遍性指的是在数学解题过程中，学生需要对问题进行多角度、多方面、全方位的分析与审视，要从常规思维的反向视角出发，推导数学知识的理论和原理，从而简化问题理解的难度，提高问题解决的效率.新颖性指的是学生运用逆向思维解答数学问题时，要摒弃传统的循规蹈矩式问题分析方法，突破固化思维的束缚，可以采用更为灵活的反向思考方式，对相关知识进行多方面的深入研究，进而厘清问题解答的思路，找到更出人意料的数学解题方法.批判性指的是学生在运用逆向思维解题时，需要克服思维定式，打破以往的问题解析模式，摒弃传统的常规化解题途径，自觉找寻与众不同的正确解题方法.

二、初中数学解题教学培养学生逆向思维的具体措施

（一）引导逆向思维应用，培养逆向思维解题意识

数学教师若想提高学生运用逆向思维解答数学问题的能力，就要先培养他们应用逆向思维解题的意识，使其掌握正确高效的逆向思维运用方法，体会到逆向思维应用的作用和意义，进而更加自觉地训练他们灵活运用逆向思维的能力.

首先，数学教师需要结合教材知识，引导学生探究逆向思维的内涵，感悟逆向思维的应用意义.例如，在教授华师大版初中数学七年级上册第二单元“绝对值”知识时，教师需要引导学生从正、反两方面视角出发，对绝对值的概念、性质进行深入研究.比如，学生通过分析教材中的案例，能够知道正数的绝对值是它本身，而负数的绝对值则是这个数的相反数，这里初步涉及逆向思维.对此，教师可以结合绝对值的定义设计逆向思考问题，如“已知|m|=-m，则m的取值范围是什么？”在解答上述问题时，学生需要根据绝对值的定义，运用逆向思维思考-m与m之间的关系，通过反向推导，得到m的取值范围.学生通过解答这一问题，能够初步领悟逆向思维的内涵，了解逆向思维的应用场景.

其次，教师再借助案例习题教授学生逆向思维的正确运用方法，让他们更加直观地感受逆向思维解题的优势，进而逐渐形成较强的逆向思维应用意识.以华师大版九年级上册第二十一单元“二次根式”课程为例，教师可以围绕此部分知识设计数学习题，引导学生运用逆向思维推理问题答案.比如“某一数学方程的根为-2和3，求这个方程.”针对这个问题，教师需要引导学生了解二次根式和一元二次方程相关的知识有哪些，同时，运用因式分解法探究此问题的解决方法.比如，学生可以先根据题目内容设一个方程，如a（x+2）（x-3）=0，然后，他们再对a进行取值代入（不含0），通过多次反向推理运算，得出最终答案.在此过程中，学生能够对已知条件和未知结果进行互逆推导，用反方向探究的方式快速得出问题结果，同时，初步掌握逆向思维的运用方法，形成良好的逆向解题意识.

（二）开展逆向思维训练，提高逆向思维解题能力

教师为了更加高效地提升学生逆向思维运用能力，提高他们数学解题的效率，需要开展有效的逆向思维训练活动.教师可以围绕各单元知识点开展数学专题训练活动，为学生提供更多逆向思维应用的机会，引导他们从反向角度出发，探究数学问题的逆向解法，借此提升其将复杂问题简化的水平，使其更加扎实地掌握逆向思维应用方法，从而提升其逆向解题的能力.

1.逆向判定数学理论

判定数学定理、判断数学理论是最常出现，也是最为基本的一个数学问题类型，这对于加深学生对抽象数学概念和理论的理解具有重要意义，同时，这也是锻炼他们逆向思维能力较为基础的一类题型.基于此，教师需要培养学生的逆向思维，使其能够从反向角度出发，以逆向推断或判定的方式探究问题结论，使其更加快速地找到数学本质，从而提升解答判定类数学问题的效率.

以华师大版七年级数学上册第五单元“平行线的判定”课程为例.在巩固平行线的性质和判定知识时，教师可以设计如下习题：图1中∠1=∠3，∠2=∠4，∠6=∠8，其中能够判定直线a与直线b平行的条件有哪些？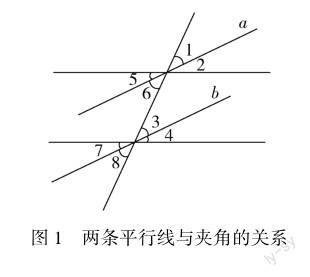

此题的目的是考查学生是否掌握平行线的判定方法.对此，学生需要运用逆向思维，结合图中信息，从多个角度出发判定直线a与直线b平行，同时推断各角之间的关系，然后再从问题中选出符合要求的条件.在解题过程中，学生通过探究各项信息之间的内在关系，找到更为灵活、更为高效的问题解答途径，通过反向推导，快速得出问题答案，从而提升数学解题的效率.

2.逆向解析数学题目

分析和理解数学题目是解答数学问题的第一个步骤，也是实现高效解题的关键环节，学生若能透彻理解题目的意思，了解出题者的意图，同时知道题目所考查的相关知识，则可以更加快速地厘清解题思路，找到更为精准的解题路径，从而提升问题解答的效率与质量.在这里需要注意的是，学生若是只依靠常规的正向解题思维研究数学问题，则很容易陷入出题者所设下的“陷阱”之中.因此，教师需要教授他们逆向检测方法，使其能够运用逆向思维检查习题结果的准确性，以此来避开“隐秘的陷阱”，提高解答数学问题的准确率.

在数学问题逆向解析过程中，教师可以先引导学生逆向分析题目内容，探寻问题中的数学本质，然后再提炼其中的关键信息，同时根据已知条件，结合相关数学知识对其进行合理运算.之后，学生再运用逆向思维检查习题结果，确保习题解答的正确性.以华师大版七年级数学下册第六单元“解一元一次方程”课程为例.教师可以设计如下问题：李雷今年的年龄是8岁，他祖父的年龄是62岁，问多少年后，祖父的年龄是李雷年龄的4倍.在解题过程中，教师需要带领学生先深入研究习题题目，探寻出题者的考核意图.比如，此题考查的是一元一次方程知识，其关键点不仅是“多少年后”，还包括“4倍”，所以，学生不能简单地计算李雷和祖父的年龄值，而是要围绕4倍年龄差进行年限计算.对此，学生可以先把“多少年”设置为未知数x，然后再根据题目中的提示信息列出一元一次方程，即8+x和62+x，之后再结合4倍年龄差对方程式进行求解，最终得出“10年后”这一结果.之后，学生需要将10代入原题之中，再一次确认10年之后祖父的年龄为李雷年龄的4倍，用逆向思维检查结论的准确性.学生通过深入解析数学题目，逆向验证问题结果，既可以躲避问题“陷阱”，提高解题的准确率，又能形成良好的逆向验证意识，提高逆向思维能力.

3.逆向证明数学定理

数学教师教授学生数学定理的逆向证明方法，是提高他们的逆向思维能力，使其更加透彻地理解数学概念性、理论性知识，提高学习质量的一种有效授课方法.逆向证明指的是从数学问题的结论出发，对其进行反方向推导，由果反向推理出问题的因，然后再根据因果关系，得出问题的最终答案.学生运用逆向证明法解答数学问题，能够更加快速地解答一些难以用正向推导法解决的复杂性问题，进而提升解题的效率与能力.逆向思维证明法包括反证法、逆证法和分析法.比如，学生若想证明数学不等式，可以从习题结果出发，逆向求出问题的初始条件，从而找到新的解题途径.

以华师大版八年级上册第十三章“等腰三角形的判定”课程为例.学生通过学习此单元知识，能够知道“等腰三角形的两个底角不能是钝角，也不能是直角，只能是锐角，而此图形的顶角则可以是钝角，也可以是直角”这一定理.在逆向思维训练活动中，教师可以围绕此定理设计证明习题.例如，针对图2中的等腰三角形，证明此图形的两个底角必为锐角.

對此，在逆向证明过程中，学生需要先做出假设，即假设∠B和∠C同为直角或钝角，然后计算三角形三个内角之和，而这两种角的内角之和均大于180°，这与三角形的内角和为180°定理相悖，由此便可推断出等腰三角形的两个底角既不能是钝角，也不能是直角.而根据这一结果进行反向推理，便可证明等腰三角形的两个底角必为锐角.学生运用逆向证明方法证明数学定理的正确性，既可以突破定势思维的束缚，提高逆向思维的运用能力，又能降低证明题的错误率，提高反向证明的质量.

4.逆向运用数学法则

初中数学教材中所包含的数学公式或运算法则，有一部分是具有双向性特点的，相互之间可以进行合理逆转.对此，教师可以利用这部分知识点的特征开展逆向思维的培养活动，引导学生运用数学公式相互逆转的方法解答习题，以此来提高他们运用逆向思维解题的水平.比如，针对某个算式习题，教师可以引导学生运用公式的逆向使用方法，或者采用排除法对其进行运算和解答，从而快速得出算式结果.数学公式或法则的逆向运用不仅可以拓宽学生的运算思路，还能借此培养他们另辟蹊径的解题意识，同时，提高其一题多解、逆向解题的能力.