基于APOS理论的集合概念教学设计

田丽娜

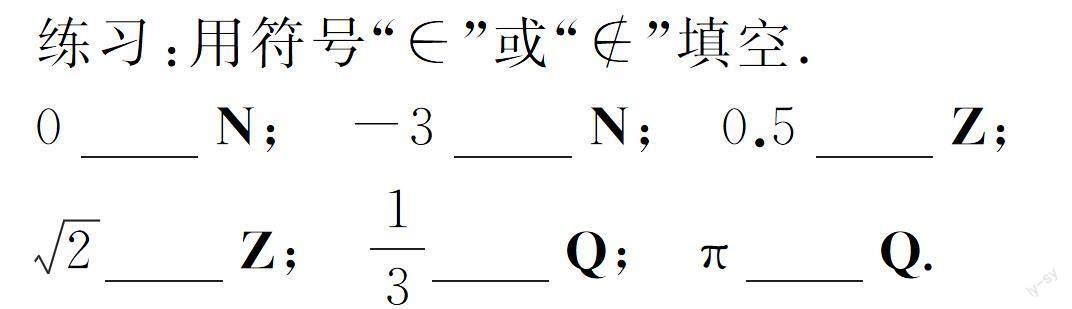
摘要：集合是高中数学学习的基础，也是高中数学学习的工具.对于刚从初中升到高一的学生而言，面对集合这一抽象的概念，往往理解不透.APOS理论是一种建构主义学习理论，它认为学生学习数学概念的过程是一个建构的过程，分为操作、过程、对象、图式这四个阶段.在APOS理论的指导下，以“集合”为例，进行四个阶段的教学设计.

关键词：APOS理论；数学概念；集合；概念教学

集合是高中阶段数学课程引入的第一个概念，是整个高中数学课程内容的基础，对后续内容的学习非常有帮助，在整个高中阶段数学内容中有着举足轻重的地位.可见，学好集合至关重要.然而，不少学生对集合概念的理解却存在着误区，在做题时出现了很多问题.美国学者EdDubinsky等人提出的APOS理论对数学概念的教学具有指导作用.本文中要解决的问题就是如何运用APOS理论指导集合概念的教学.

1 APOS理论概述

APOS理论由美国数学教育家杜宾斯基提出＼.APOS是由action（操作）、process（过程）、object（对象）、schema（图式）这几个英文的首字母组合而成的.这个理论认为，在数学的学习中，如果教师能引导学生经历操作、过程以及对象这几个阶段，那么一般情况下，学生就能够在建构、反思的基础上把它们组成图式，从而厘清问题的情境，顺利解决问题＼.该理论是一种建构主义学习理论，它认为学生学习数学概念的过程是一个建构的过程，建构的四个阶段应该是循序渐进的，一般来说，不可逾越，因此教师可以把APOS理论作为经验，指导学生学习数学概念.

2 概念教学概述

数学概念的学习是学生学习其他数学知识的基石，还可以培养学生的数学能力.概念教学是数学教学的重要组成部分.教学中教师要展示数学概念的形成过程，使学生能够主动建构学习过程，从而更加深刻理解这个数学概念＼.

3 基于APOS理论的“集合”教学设计

3.1 活动阶段

在小学和初中阶段，我们就已经接触过了一些集合.比如在初中阶段，在代数方面，学过自然数集合、有理数集合以及实数集合；在几何方面，学过点的集合等.观察下面的例子：

（1）1～10之间的所有偶数；

（2）黑龙江省克东县一中的全体高二学生；

（3）所有的正方形；

（4）到直线l的距离等于定长d的所有点；

（5）方程x2－3x+2=0的所有实数根；

（6）地球上的四大洋.

在例（1）中，把1到10之间的每一个偶数都作为元素，那么这些元素的全体就可以组成一个集合；在例（2）中，把黑龙江省克东县一中的每一位高二学生作为元素，这些元素的全体也可以组成一个集合.

思考：上述的例（3）到例（6）中的元素分别是什么？它们可以组成集合吗？

集合：一般地，我们把研究对象统称为元素，通常用小写拉丁字母a，b，c，……表示，把一些元素组成的总体叫做集合（简称为集），通常用大写拉丁字母A，B，C，……表示.

追问：高中学生中的跑步能手的全体是否能组成集合？

分析：高中学生中的跑步能手这一定义并不明确，很难判断某个人是否满足跑步能手这样子的说法，无法确定一个标准，所以，这样的说法表示的对象无法组成一个集合.

确定性：对于一个给定的集合，集合中的元素必须是确定的，一个元素要么是这个集合中的元素，要么不是这个集合中的元素.

互异性：一个给定集合中的元素是互不相同的.

无序性：集合中元素的位置是可以变换的，只要构成两个集合的元素是相同的，那么这两个集合就是相等的.

设计意图：根据学生已经有的认知结构，再从学生熟悉的各种具体的集合引入，重要的是将这些具体的事例进行抽象，从而得到集合的概念.教学中共讲解六个例子，从中总结集合的概念，让学生充分体会集合的含义，并用准确的语言表达集合的特征.另外，讲解一个反例，帮助学生理解集合的概念.这个阶段是操作阶段，应多提供一些感性材料启发学生进行思考.

3.2 过程阶段

如果a是集合A中的元素，那么a属于集合A，记作a∈A；如果a不是集合A中的元素，那么a不属于集合A，记作aA.

练习：用符号“∈”或“”填空.

0N；

-3N；

0.5Z；

2Z；

13Q；πQ.

设计意图：此阶段讲述元素与集合的关系，通过练习题加深学生对此概念的理解，这也是自然语言转化为符号语言的关键.符号语言的教学是整个高中数学教学的一个重点，所以要特别注意学生的符号使用是否规范，为以后的学习打下基础.这个阶段是过程阶段，要注意引导学生进行抽象概括，要求学生严谨地使用符号语言.

3.3 对象阶段

列举法：把集合中的所有元素一一列举出来，并且用花括号“{}”括起来表示集合的方法叫做列举法.

除了一些特殊集合外，还可以用什么方式表示集合呢？

例1用列举法表示下列集合：

（1）1到11之间的所有奇数组成的集合；

（2）A={x|x2=5x}.

提问：对于不等式x－7<3，你可以用列举法表示它的解集吗？

描述法：一般地，设A是一个集合，我们把集合A中所有具有共同特征P（x）的元素x所组成的集合表示为{x∈A|P（x）}，這种表示集合的方法称为描述法.

例2用描述法表示下列集合：

（1）正偶数集；

（2）被3除余2的正整数的集合；

（3）函数y=3x+5与函数y=x－4的图象的交点组成的集合.

例3请同时使用描述法和列举法表示下列集合：

（1）大于15并且小于25的所有整数组成的集合A；

（2）方程x2－10=0的所有实数根组成的集合B.

设计意图：通过几道例题，学生充分体会什么情况下使用列举法好，什么情况下使用描述法好，因为有一些题目既可以使用列举法又可以使用描述法，此时的教学也渗透给学生最优化的数学思想.经过前面两个阶段的学习后，学生已经基本掌握了集合的特征，这时学生学习集合的表示法，能够准确地使用符号语言表示集合，能够把集合看成是一个整体，从而达到对象阶段.

3.4 图式阶段

运用集合元素的性质和表示法解决实际问题.

例4若x2∈x，1，0，则x=_____________.

解析：由题意可知，x2=x或x2=1或x2=0.

①当x2=x时，x=0或x=1.当x=0时，集合的三个元素为0，0，1，不满足集合中元素的互异性；当x=1时，集合的三个元素为1，1，0，不满足集合中元素的互异性.

②当x2=1时，x=－1或x=1（舍去），集合的三個元素为-1，1，0，满足集合中元素的互异性.

③当x2=0时，x=0，不满足集合中元素的互异性.

综上可知，x=－1.

设计意图：在学习了集合的含义、集合的特征、元素与集合之间的关系、集合的表示法之后，给出几道练习题，让学生运用这些知识来解决问题，从而形成集合概念的图式.学生是否掌握了图式的连贯性可以通过一个方法来确定，即学生有没有用它来解决特定的数学问题的能力＼.在没有学习这节课之前学生关于集合概念的图式都是具体的、零散的，而新的图式是抽象的、整体的.

4 教学反思及建议

APOS理论本质上讨论的是数学学习的心理结构和心理机制的问题.心理机制可以解释个体的数学知识是如何建构的，基于这个功能，APOS理论可以作为一个理论基础，对数学概念教学进行指导＼.实践表明，基于APOS理论下的数学概念的教学能够激发学生的学习兴趣，加深学生对概念的理解.所以，在操作阶段教师可以多提供一些感性材料，启发学生进行思考；在过程阶段教师应注重引导学生进行抽象概括，将集合的自然语言转化为符号语言；在对象阶段，学生已经基本掌握了概念的形式＼，教师应引导并帮助学生理解概念的实质；通过前面三个阶段的学习，教师可以利用练习题来判断学生是否达到第四阶段，形成一个新的整体的图式.APOS理论中的四个阶段是紧密联系的，不可以把它们割裂来看.APOS理论是一种建构主义学习理论，强调学生学习的主动性，强调学生应是主动建构知识而不是被动接受，所以，教师除了要发挥自己的主导作用，还要以学生为中心，充分发挥学生的主体作用.

参考文献：

［1］濮安山，史宁中.从APOS理论看高中生对函数概念的理解[J].数学教育学报，2007（2）：48-50.

［2］乔连全.APOS：一种建构主义的数学学习理论[J].全球教育展望，2001（3）：16-18.

［3］李莉.学生学习数学概念的层次分析[J].数学教育学报，2002（3）：12-15.

［4］江春莲，胡玲.基于APOS理论和RMI原则的二次函数图象平移教学实验研究[J].数学教育学报，2020，29（6）：32-39.

［5］马晓丹.APOS理论探索的反思与超越[J].教学与管理，2020（33）：74-77.

［6］程华.APOS理论的内涵及其对中学数学概念教学的启示[J].教学与管理，2010（24）：65-66.