基于改进3D-NDT 机器人自定位算法

许振权，徐红伟

（中国计量大学机电工程学院，浙江 杭州 310000）

0 引 言

近几年，多数学者提出了一种以激光点云数据进行机器人自定位的方法，通过机载激光雷达与点云地图进行匹配来获取机器人精确的定位信息，并且这种方法是可行的[1]。在该项定位技术中，点云匹配是其关键技术，目前有的方法包括SVD（奇异值分解）、ICP 以及PCA（主成分分析）[2-5]。其中：对于SVD 和PCA 算法而言，它们的计算效率较高[6-7]，但其对输入点云的剔除异常值要求较高，并且存在误差大的缺点；而ICP 算法相对而言，误差较小，并且较为稳定。但是，对于ICP 算法，其又存在计算效率低下，计算量较大，而且对于输入点云的初始姿态有着苛刻的要求，如果没有很好地提供初始姿态，误差也会出现大偏差。在3D-NDT 算法中，其采用计算正态分布的方式作为点云配准的方法，就不同于ICP 算法，需要大量时间来计算得出配准结果，适用于机器人定位方法中[8-9]。但其在计算过程中，在没有提供输入点云的初始姿态下，匹配结果还是会存在较大误差，而且要消耗大量时间。针对该缺陷，本文提出基于ISS 特征点的改进3D-NDT 算法，来进行机器人的定位。

1 3D-NDT 算法

3D-NDT 算法是把一个三维体素内的点云数据集转换成一个连续可微的概率分布函数来进行点云匹配的算法[8-9]。它将输入点云划格分开，形成均匀规则固定大小的三维单元格，在各个单元格内就形成了一个个的点云集，通过对各个单元格内的点云集进行正态概率分布，两幅点云数据进行相互计算，不断反复，最终得到匹配的结果。在整个算法流程中，网格内的正态分布概率密度只需要计算一次，不用对每个点都进行相对应的计算和匹配操作，因此，该算法计算量不大，计算效率也较高。

3D-NDT 算法的输入参数是两幅点云数据S1、S2，输出是两幅点云变换的参数R、T。在机器人自定位中，两幅分别为机器人在当前位置扫描出来的点云图以及机器人在当前大致位置的点云地图，通过输出的R、T就可以明确知道机器人在当前点云地图中的确切位置。

3D-NDT 算法具体步骤为：

1）将输入点云进行空间划分，分开为大小固定的各个小的空间，也叫体素，其中体素大小决定了两幅点云配准之间的精度，体素的尺寸越大，点云配准的误差越大，反之，则越小。对于时间来说，体素尺寸越大，时间反而越小。

2）把输入的参考点云投影到各个体素上。

3）计算每个体素的正态分布概率密度函数参数：

式中：yk,k= 1,2,…,m表示体素内的各个点；Σ描述各个体素内的协方差。

4）将第二幅点云按照初始输入R、T进行变换。

5）第二幅点云落于各个体素，计算其相应的概率分布函数PDF。

6）使用最大似然函数得到最终结果。

2 改进的3D-NDT 算法

2.1 算法原理

改进的3D-NDT 算法在于为3D-NDT 算法提供一个初始姿态估计，先对输入点云进行ISS 特征点提取，然后计算这些特征点的特征直方图（FPFH），根据这些FPFH 进行对应点匹配[10]，用RANSAC 去除错误对应关系，得到初始姿态估计结果。改进后的3D-NDT 算法如图1 所示。

图1 改进的3D-NDT 流程图

2.2 算法实现

2.2.1 ISS 特征点

想要获取两幅点云的变换关系，提取特征点是其中的关键所在[11]。ISS 特征点是一种通过与邻域信息建立联系，并利用特征值之间的关系来表示点特征程度的方法。

ISS 特征点提取步骤为：

1）对输入的每个查询点设定一个搜索半径。

2）计算查询点与邻域内各个点的欧氏距离，并设定相关的权值大小。

3）计算每个查询点与邻域内所有点的协方差矩阵。

4）计算协方差矩阵的所有特征值，并将其排序，采用从大到小的排序方式。

5）设置阈值，满足阈值条件的即为ISS 特征点。

ISS 特征点示意图如图2 所示。

图2 ISS 特征点示意图

2.2.2 FPFH 特征

FPFH 特征可以描述点的特征，是点特征的描述子，是基于PFH 做的，提高了计算效率。使用FPFH 特征提取，可以在一定程度上提高对点云的认知，实现点云的高层次认知。

FPFH 特征的计算方法如下：

1）对于点云模型中所有点先以半径r邻域计算三个特征算子，在此基础上，统计邻域内所有区间的点数量所占百分比得出简化点特征直方图SPFH。

2）对于每个点都需要另外包含2r半径内的其他一些点。对于新包含进来的这些点在第一步计算中得到的SPSH 进行加权并与点p本身的SPFH 求和，最终得到点p的FPFH，其中，FPFH 的计算公式如下：

2.2.3 RANSAC 去除错误对应关系

得到点云中每个点的FPFH 之后，应用直接对应估计算法得到两个点云中的对应关系。而在对应匹配的计算中，由于点云中操作异常噪声点会带来匹配结果存在很大的误差，从而导致配准失败，因此，消除错误对应关系是关键。

采用RANSAC 的方法剔除错误的点对关系，其主要用于解决样本中的外点问题，它能有效地剔除一些不符合最优参数模型的点，例如噪声、无效点等[12]。RANSAC 算法步骤如下：

1）在样本中随机采样K个点；

2）对K个点进行模型拟合；

3）计算其他点到该拟合模型的距离，并设置阈值，如果大于阈值，则为外点，并删除，小于阈值则保留；

4）采取内点最多的模型重新估计模型并进行改进。

在剔除错误的点对关系后，就可以根据剩余的点云关系进行匹配，得到一个比较正确的初始姿态估计，当作3D-NDT 算法的初始姿态估计。

3 实验结果与分析

本文在机器人上搭建三维扫描平台进行相关实验数据获取，水平采用360°方位扫描，垂直采用180°上下扫描，水平垂直的扫描角度都为0.5°，因此，可以得到点云数为260 642 的点云数据。再经过体素降采样与离群点去除来减少计算量以及去除异常点对配准结果的影响[13]。室外两幅场景点云数量为15 241 和15 452，室内两副场景点云数量为17 231 和17 624。实验测试数据如图3 所示。

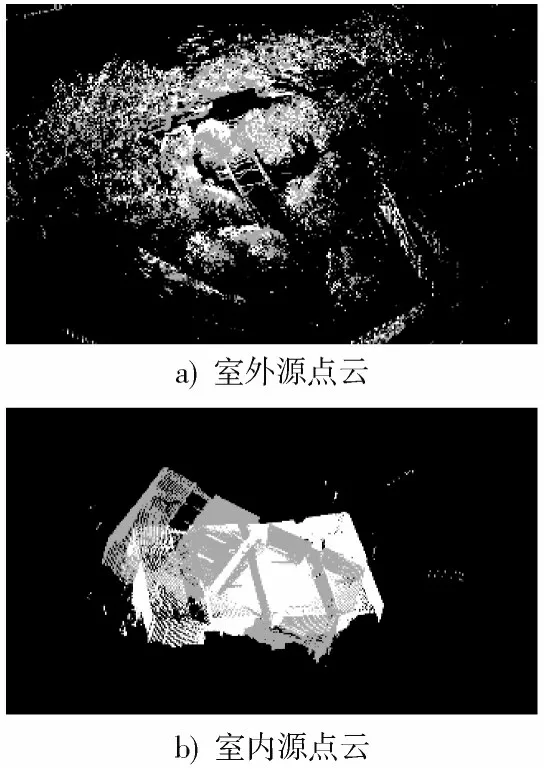
图3 室内外测试点云图

对点云先进行ISS 特征点提取，如图4 所示。在经过ISS 特征点提取后，室外一幅场景点云ISS 特征点数据为841个，室内一幅场景点云ISS特征点数据为865 个，可以看到，在ISS 特征点提取后在保留源点云一些特征的条件下，大大降低了点云数量，从而也让点云的初始匹配速度得到了一定的提高。

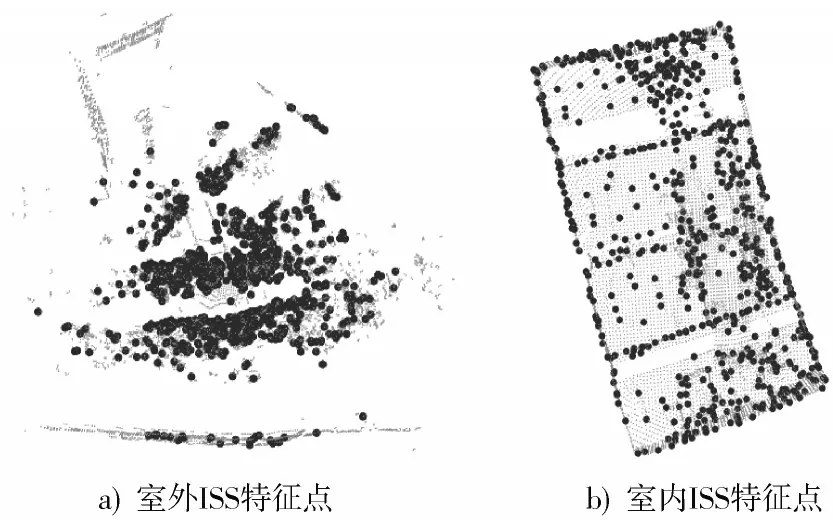
图4 ISS 特征点提取图

采用均方根误差（RMSE）和时间作为性能评价指标，其中，RMSE 可以描述匹配结果的好与坏，RMSE 数值越小，描述两幅点云匹配之后差距越小，匹配结果更好，反之，则越差。时间是指在计算机输入两幅需要配准的源点云后，到计算机输出结果R、T数值之间所需要的时间长短。实验对比结果如表1 所示。

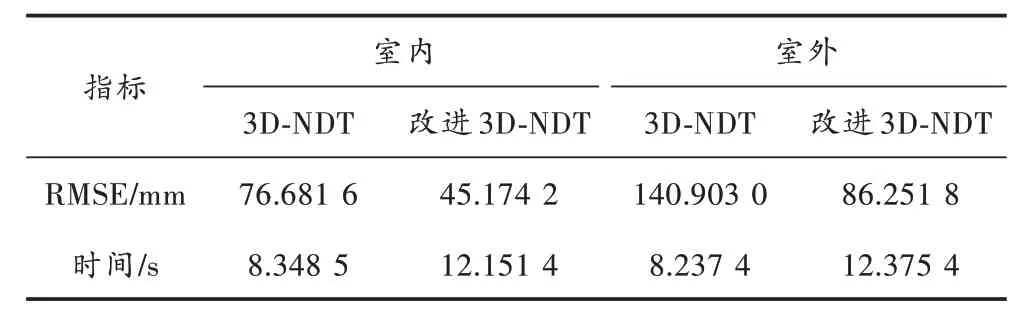
表1 实验结果对比

改进3D-NDT 算法在精度上得到了一定的提升，在室外场景定位中RMSE 提高了54.651 2 mm，室内场景定位中RMSE 提高了31.507 4 mm，改进的3D-NDT 算法配准效果也比较理想。点云配准实验结果如图5 所示。

图5 实验结果对比图

4 结 语

本文提出的改进3D-NDT 的配准算法相比传统的3D-NDT 算法，对源点云进行了基于ISS 特征点提取获取初始姿态估计，提高了其3D-NDT 配准的精度，为机器人自定位提供了更加准确的定位结果。