基于检测残差消除的CP-OTFS 系统信号检测算法

明映成，常 俊，2，唐红刚，杨 川，潘润勇

（1.云南大学信息学院，云南 昆明 650500；2.云南省高校物联网技术及应用重点实验室，云南 昆明 650000）

0 引 言

为面对未来社会万物互联、泛在智能的需求以及不同场景下的极其可靠通信，第六代移动通信技术（6G）的研究逐渐成为当下科研热点。IMT-2030（6G）推进组在6G 网络架构愿景中指出，未来6G 网络需要支持高移动性环境下的超可靠通信，以满足地球低轨卫星、高速列车、无人机等通信应用场景[1]。然而，当前移动通信系统中采用的是正交频分复用（Orthogonal Frequency Division Multiplexing, OFDM）技术，其会因高移动性环境下导致的高多普勒频移造成子载波间干扰，在终端移动速度大于500 km/h 的高多普勒信道环境下，OFDM 通信系统的性能是完全崩溃的[2]。

正交时频空（Orthogonal Time Frequency Space,OTFS）调制是一种能够面对高速移动通信特性的先进调制技术。OTFS 通过将发送数据经预处理和星座调整后映射到时延-多普勒（Delay-Doppler, DD）域，并经过一系列的二维变换使得同一个发送OTFS 帧内的信号捕获到DD 域等效信道的稀疏性，都经历了与时间选择无关的慢衰落，从而获得信道时间和频率的全分集增益以及更优越的抗干扰性能[3]。OTFS 系统作为一种搭载新型调制方式的通信系统，在信号传输的过程中不可避免地会因多径效应而引起码间干扰[4]。同OFDM系统一样，可以加入循环前缀（Cyclic Prefix,CP），接收端可以通过将干扰符号的循环前缀与相应干扰符号的主要部分相消来减轻这些干扰[5]。CP-OTFS 系统中CP 的添加方式与OFDM 系统相同，因此CP-OTFS 系统可以通过向OFDM 系统添加预处理和后处理块来实现[2]。CP-OTFS 与现有的OFDM 系统更加兼容，对OTFS 调制在实际应用研究中具有重大意义。

在通信系统中，信号检测主要是为了均衡信道的影响以及消除信号接收端可能遇到的误差和失真。由于OTFS 系统中通过ISFFT 变换操作将每个调制符号扩展到整个时频资源网格，等效信道矩阵维数大于OFDM 系统，这显著增加了信号检测的复杂度。此外，在OTFS 系统中信息符号在时变信道传输过程中的变化与其DD域的索引有关，且接收DD 域信号存在额外相位项，这不利于OTFS 系统的信号检测算法设计[6]。因此，研究低复杂度CP-OTFS 信号检测算法成为学者们广泛关注的方向。CP-OTFS 系统信号检测算法主要分为两类：线性检测算法和迭代检测算法。线性检测算法主要是线性最小均方差（Linear Minimum Mean Square Error,LMMSE）算法、迫零（Zero - Forcing, ZF）算法[7-10]。LMMSE、ZF 算法结构简单、易于实现，在传统通信系统中也被广泛使用。但在OTFS 系统中，等效信道的建模采用的矩阵维度远远大于传统通信系统，在涉及到计算逆矩阵时会造成极高的计算复杂度。迭代检测算法结合接收信号的相关性质，通过迭代更新检测值，最终得到最优解。当前得到最广泛研究的是文献[11]中提出的消息传递（Message Passing, MP）算法及其改进算法[12-14]。MP 算法的计算复杂度依赖于信道矩阵的稀疏性，在复杂的多径信道中不易收敛，迭代次数增加，带来了较高的计算复杂度。

针对当前CP-OTFS 系统信号检测算法复杂度高的问题，本文通过分析CP-OTFS 系统时延-时间域的输入-输出关系，在低复杂度的初始检测后，提出一种基于检测残差消除的CP-OTFS 信号检测算法，并在500 km/h的高移动场景中对该算法进行了仿真分析。

1 CP-OTFS 系统模型

CP-OTFS 系统信号处理流程图如图1 所示。

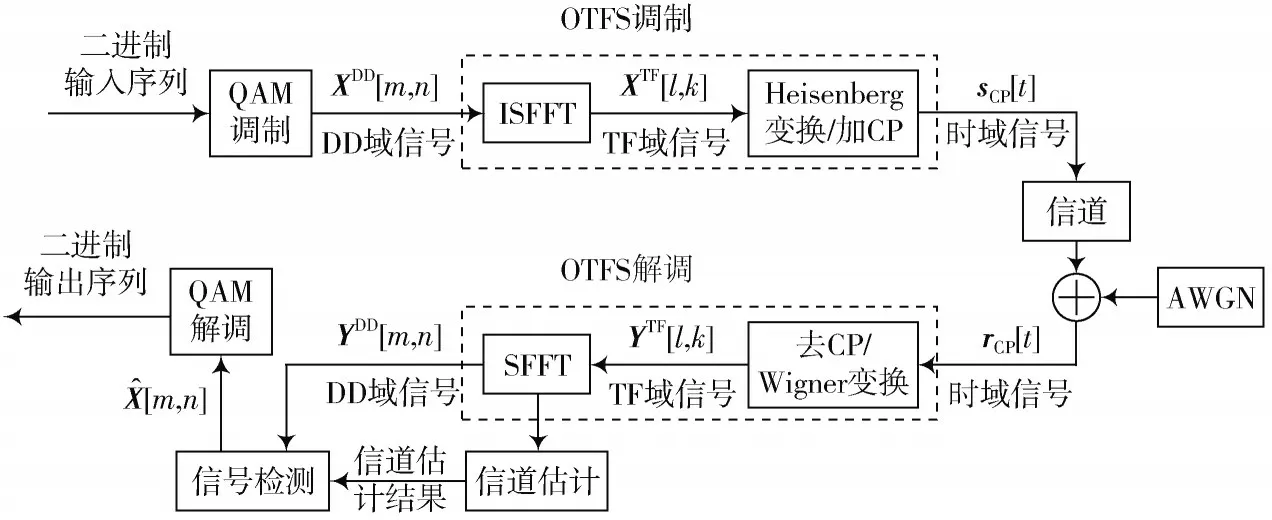
图1 CP-OTFS 系统框图

1.1 发送端

在OTFS 系统中二进制输入序列经过QAM 调制后，将发送数据符号映射到维度为M×N(M,N∈N+)的二维DD 域平面，得到DD 域信号XDD[m,n](0 ≤m≤M-1,0 ≤n≤N- 1)。其中：M是沿时延方向的资源单元维度，表示OTFS 系统中的子载波数；N是沿多普勒方向的资源单元维度，表示时隙数。子载波间隔为Δf，单个时隙长度为，DD 域资源网格时延分辨率为τ0=，多普勒分辨率为。XDD[m,n]通过逆辛快速傅里叶变换（Inverse Symplectic Fast Fourier Transform, ISFFT）映射到时频网格上的时频（Time-Frequency, TF）域信号XTF[l,k](0 ≤l≤M- 1,0 ≤k≤N- 1)，矩阵化表示为：

式中：FM、表示M点傅里叶变换和N点傅里叶反变换；(·)H表示共轭转置。

随后时频调制器将二维符号XTF[l,k]通过海森堡变换（Heisenberg Transform）转换为时域信号s[t]：

式中vec(·)表示矩阵的向量化[2]。这一步对标OFDM 系统中的IFFT 操作，也即将一个时频域调制的信号变换为一个实际发送的时域信号模型。

CP-OTFS 系统中，向量s分块添加入CP 后得到：

式中：IN表示单位矩阵；⊗为克罗内积；ACP=被称为CP 增加矩阵，，等价于IM最后Lmax行，帧结构如图2 所示。离散时间信号sCP[t]在通过脉冲整形后（本文采用矩形脉冲整形）得到sCP(t)，通过发射天线将调制信号发送到高速移动场景信道中。

图2 CP-OTFS 时域帧结构

1.2 接收端

在接收端，接收天线在接收到信号后通过匹配滤波和时域采样得到离散时间信号rCP[t]，并去除CP 得到：

YTF[l,k]通过辛快速傅里叶变换（Symplectic Fast Fourier Transform, SFFT）映射回DD 域：

1.3 信 道

本节中考虑具有P条传播路径的信道模型，对于第i条路径，i= 1,2,…,P，路径复增益为gi，延迟和多普勒频移分别为τi和νi。在DD 域中，归一化的延迟和多普勒频移分别为ℓi=MΔfτi和κi=NTνi。设归一化延迟集合为，每个ℓi对应路径的归一化多普勒频移集合为，延时为ℓ时的多普勒响应表示为：

式中：νl(κ)表示信道增益的变化：表示多普勒频移；表示信道的时变性。时域的输入-输出关系可以写成：

式中w为信道噪声[15]。

为了表示的简洁性，本文后续部分将忽略噪声的影响，去除CP 后接收信号表示为：

式中[·]M表示取余运算，这是由加CP 后的循环特性决定的。由于加入了CP，接收信号r无码间干扰，时域信道矩阵G∈CMN×MN的建模如图3 所示。

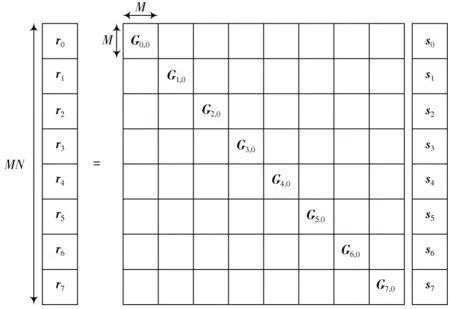
图3 时域信道矩阵

将s和r分块表示，，r=。分块矩阵的输入-输出关系表示为：

式中：rn、sn∈CM×1是s和r的子向量；Gn,0∈CM×M是G的对角子矩阵：

2 时延-时间域输入-输出关系分析

结合1.3 节分析，可以得到分块的时域输入-输出关系为：

对s和r进行并行表示，得到其时延-时间（Delay-Time, DT）域的表示形式：

其子向量间的关系可表示为：

XDT和YDT向量化表示为：

DT 域输入-输出关系写成：

式中：HDT=PT·G·P∈CMN×MN，PT·P=IMN为DT 域信道矩阵。子向量形式输入-输出关系写成：

由式（18）可知，在DT 域中CP-OTFS 系统的输入-输出关系可表示为向量间逐元素的乘积而非矩阵运算，利用此式进行信号检测复杂度是较低的。

3 低复杂度信号检测算法

3.1 初始检测

在CP-OTFS 系统中，由于每一个时域块都加入了CP，在信号检测时可以根据块形式同步进行，即将信道矩阵分块，这将大大降低检测的复杂度。TF 域的输入-输出关系可以写成：

结合最小均方误差（MMSE）算法，初始检测信号的TF 域形式为：

式中：(·)*表示共轭；表示噪声方差。

DT 域形式写为：

3.2 检测残差消除的信号检测算法

基于DT 域输入-输出关系分析，本文提出了一种DT 域检测残差消除的信号检测算法。将初始检测值代入系统输入-输出关系式，得到以检测信号为发送信号的系统输出信号，计算检测输出信号与实际接收信号间的残差值，然后将残差值回代输入端更新检测信号，迭代计算以逐步消除残差，信号检测流程如图4所示。

图4 信号检测算法流程图

具体步骤如下：

1）以DT 域的初始检测值为系统输入代入式（18），定义初始检测残差为：

2）进入迭代计算过程。以此残差为反馈，回代DT域输入-输出关系式得到反馈值：

3）结合反馈值得到DT 域的残差消除信号：

4）由于最终输出的二进制比特流是由加载在DD域的QAM 符号解映射而来，需在DD 域结合QAM 字母表A={a1,a2,…,aQ}进行逐符号的最大似然（Maximum Likelihood, ML）检测：

5）以前后两次迭代检测值的差值更新检测残差值：

3.3 计算复杂度分析

本节中，通过统计信号检测过程中乘法的运算次数作为评判算法计算复杂度的指标，用O(·)表示计算复杂度。初始检测算法中，计算的乘法计算次数分别为2MNlog2M、MNlog2M、3MN、MNlog2M，因此初始检测算法计算复杂度为。检测残差消除检测算法中，计算的乘法次数为MNL，式中L为归一化延迟集合的维度，表示信道各径参数中非重复时延索引数。在每一次迭代中计算以及更新的乘法次数分别为MN(2L+ 1)、2MNlog2N、MNL。设最大迭代次数为I，算法整体计算复杂度为。由于算法在时即输出结果，实际迭代次数会小于I，此处计算的是最大计算复杂度。表1 给出了LMMSE 算法[7]、MP 算法[11]和本文提出算法的计算复杂度，S为观测节点数，Q为QAM 调制阶数。

表1 算法计算复杂度

4 仿真结果与分析

为验证基于检测残差消除的CP-OTFS 系统信号检测算法在高移动场景下的检测性能，本节对未编码的CP-OTFS 系统进行性能仿真，并在相同条件下对比了LMMSE 和MP 算法。仿真信道采用3GPP 标准中的扩展车辆A（EVA）信道模型，模拟9 条路径，每条路径的多普勒频移遵循Jakes 频谱，即，其中umax表示终端移动速度，取500 km/h，θi在[-π,π ]均匀分布。使用4QAM 调制方式，取子载波数M= 64，时隙数N=16，载波频率fc= 4 GHz，子载波间隔Δf= 15 kHz，CP 长度LCP=lmax，采用理想信道估计。

图5 给出了本文算法在不同信噪比下收敛时与MP算法平均迭代次数的对比，由算法步骤中的停止准则决定。随着信噪比的增加，算法收敛加快，由图5 可知，本文所提出算法收敛速度快于MP 算法。

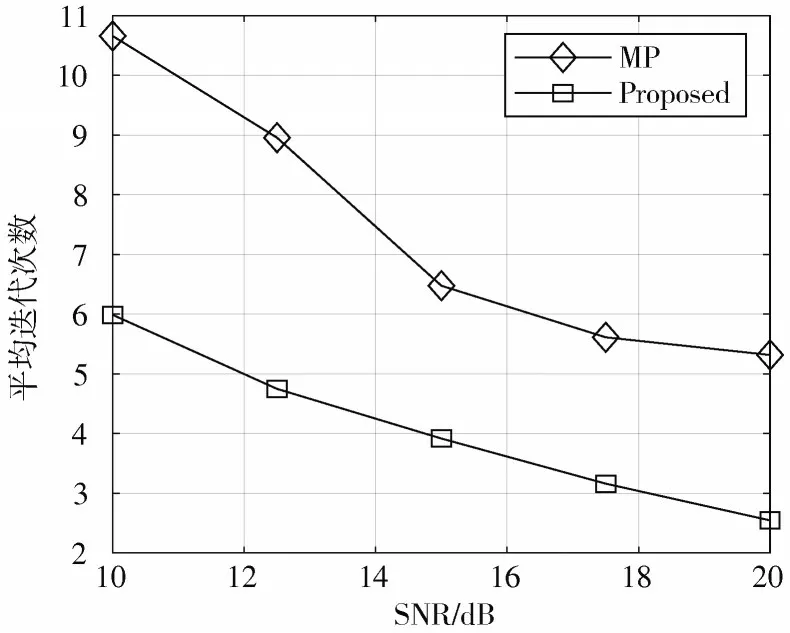
图5 算法收敛所需迭代次数

初始检测算法与三种不同的信号检测算法的误码性能如图6 所示。由图6 可知，初始检测算法在经过检测残差消除后，误码性能有显著提升。此外，由于检测残差消除算法在迭代消除检测残差的过程中，亦消除了部分因噪声和多径效应带来的干扰，因此在低信噪比时表现出了比其他算法更优越的误码性能。本文所提算法在实验仿真条件下，信噪比为15 dB 时，误码性能比LMMSE 算法提升了2.79 dB，比MP 算法提升了1.76 dB。由于本文所提算法误码性能与初始检测算法相关，在信噪比大于20 dB 时误码性能略逊于其他算法。

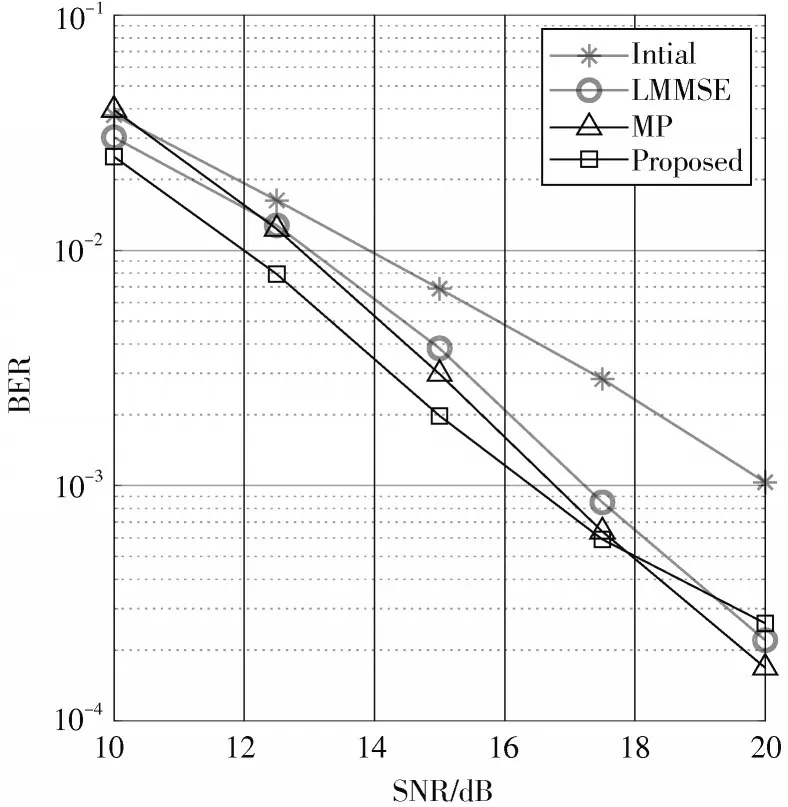
图6 不同检测算法误码性能比较

图7 给出了M= 64 时三种信号检测算法计算复杂度比较曲线。

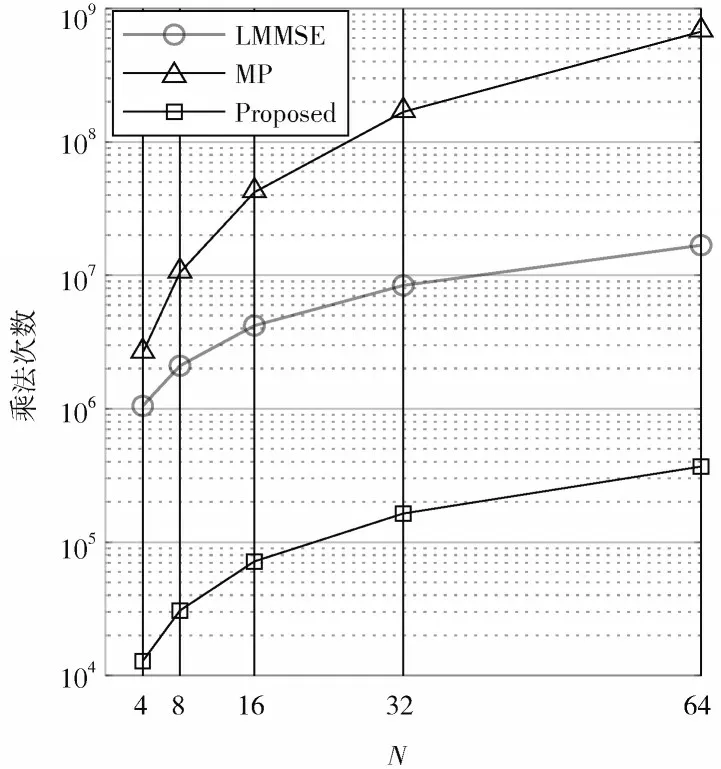
图7 不同检测算法计算复杂度比较

本文所提出算法在实现过程中不涉及矩阵求逆运算，不同域信号变换时利用FFT 算法加速运算，降低了计算复杂度。由图7 可知，本文提出算法在计算复杂度上具有更大优势。

5 结 语

在高移动性场景下的通信中，CP-OTFS 系统有着更显著的抗码间干扰能力和与当前通信系统的兼容性。本文针对当前CP-OTFS 系统信号检测算法复杂度较高的问题，提出了一种在低复杂度初始检测后基于检测残差消除的信号检测算法。结合DT 域CP-OTFS 系统的输入-输出关系式，迭代计算消除检测残差，达到全局最优。仿真结果表明，本文提出的检测算法在低信噪比下误码性能优于LMMSE 和MP 算法，并且收敛更快。此外，该算法对比其他检测算法具有更低的计算复杂度。