基于干扰观测器的倒立摆抗干扰反步控制研究
2024-01-03李艳芳王成华魏明鉴
李 珺, 李艳芳, 王成华, 魏明鉴
(潍坊工程职业学院机电工程学院, 山东 潍坊 262500)
倒立摆系统是一个非线性、欠驱动、不稳定的机械系统,控制过程中,由于其特殊的结构可有效反映出控制系统鲁棒性和抗干扰性能的优劣。因此,在控制领域中,倒立摆系统是检验新的控制策略和算法的经典控制系统[1-3],倒立摆为机器人系统中的许多模块提供了大量模型[4-5],有时也被用作实际控制问题的代表性模型,如机器人的手臂运动或火箭的发射[6-7]等。为了解决单级直线倒立摆系统的镇定控制和轨迹控制问题,线性自抗扰控制[8-9]、自适应神经网络[10-12]、最优控制[13-14]和预测控制[15]等各类算法相继应用于研究中。在已有的研究中,多数算法都依赖于精准的动力学建模[16-17]与线性化过程[18-19],从而导致控制算法在鲁棒性和抗干扰能力方面的不足, 难以适用于实际工程环境。为了解决上述问题,本文提出了一种基于干扰观测器的倒立摆抗干扰反步控制方法。将单级直线倒立摆的数学模型改为受干扰时的形式,设计非线性干扰观测器对干扰进行实时估计,并基于干扰的估计值和反步控制方法,采用 Lyapunov 稳定性理论设计控制器,得到基于干扰观测器的单级直线倒立摆抗干扰反步控制器,实现对干扰的抑制。仿真结果表明,该算法能够有效抑制干扰对单级直线倒立摆控制效果的影响。该研究对以倒立摆为模型的实际控制系统的抗干扰性能提供了改善方法。
1 单级直线倒立摆系统的数学模型
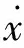

图1 单级直线倒立摆系统
由牛顿第二定律,可得小车水平方向为
(1)
摆杆水平方向受到的力为Fx,竖直方向受到的力为Fy,因此在摆杆水平方向受力为
(2)
摆杆竖直方向为
(3)
摆杆力矩平衡为
(4)
将式(2)代入式(1),将式(2)和式(3)代入式(4),可得
(5)
(6)
式(5)和式(6)为单级直线倒立摆数学模型,可见单级直线倒立摆系统是一个不稳定、非线性、欠驱动的机械系统。在实际环境中,单级直线倒立摆易受到不确定的干扰,因此将单级直线倒立摆在受到干扰时的数学模型改写为
(7)
(8)
式中,d为不确定干扰。下面将依据此数学模型,设计单级直线倒立摆非线性干扰观测器。
2 单级直线倒立摆非线性干扰观测器设计
设计非线性干扰观测器为
(9)
其中
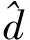
非线性干扰观测器的增益n定义为
(10)
干扰观测器的观测误差定义为
(11)
(12)
其中
(13)
若使微分方程的解指数收敛,则
(14)
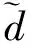
(15)
3 基于干扰观测器的单级直线倒立摆抗干扰反步控制器设计
基于干扰观测器的单级直线倒立摆抗干扰反步控制原理框图如图2所示。
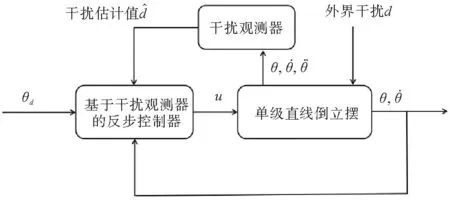
图2 倒立摆系统的抗干扰控制原理框图
第1步 定义子系统的误差变量
e1=θ-θd
(16)
取e1导数,得
(17)
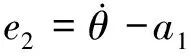
构造Lyapunov函数为
(18)
并取其导数,即
(19)
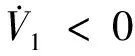
a1=-c1e1
(20)
其中,ci(i=1,2)>0为控制增益。
(21)
(22)
第2步 对虚拟误差变量e2取导,得
(23)
构造Lyapunov函数为
(24)
取其导数为
(25)
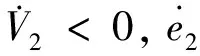
(26)
得到
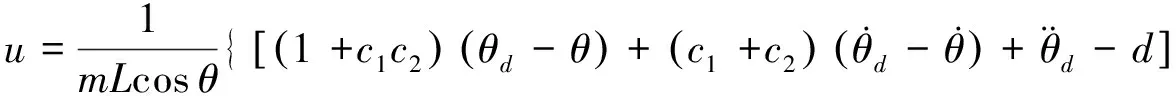
(27)
由式(15),得

(28)
小车运动最终位置由基于干扰观测器的单级直线倒立摆的抗干扰反步控制器u联立式(5)运算得到。
4 仿真分析
为验证本文算法的有效性,采用文献[20]中单级直线倒立摆的具体参数进行仿真,搭建Matlab/simulink仿真平台,单机直线倒立摆参数如表1所示。

表1 单级直线倒立摆参数
(29)
4.1 单级直线倒立摆受到连续干扰信号时的控制效果
在受到连续正弦信号干扰时,连续正弦干扰信号d=1.5sin0.5t,干扰及干扰观测器估计值如图3所示。由图3可以看出,干扰观测器能够稳定估计连续正弦干扰信号,估计值准确且有效。
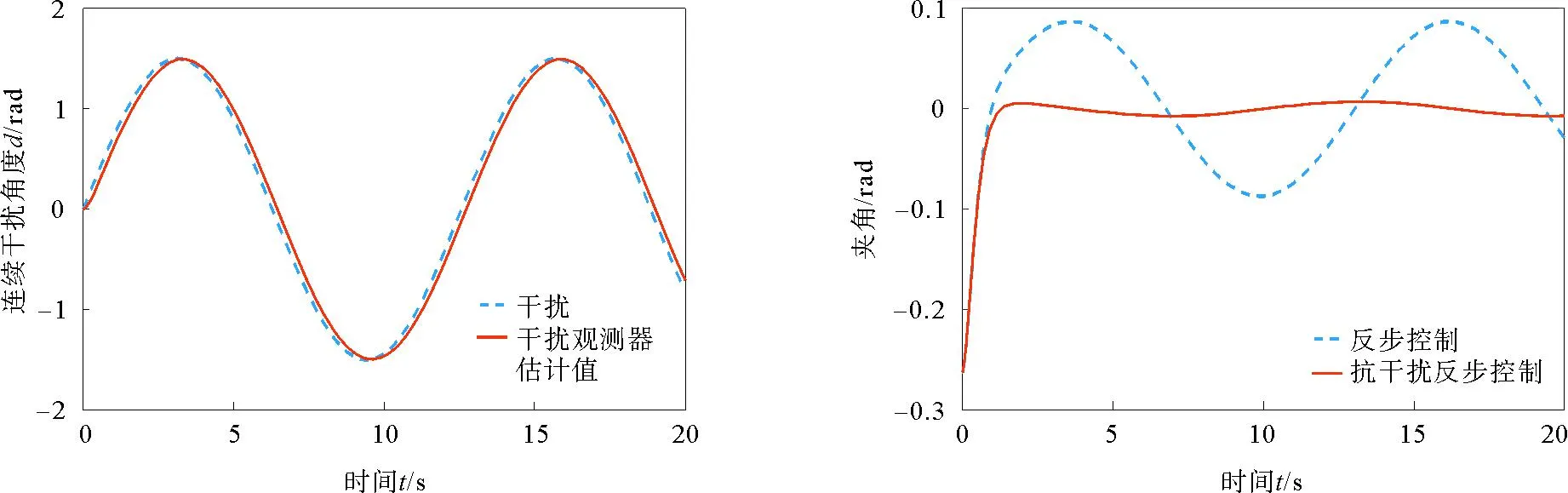
图3 干扰与干扰观测器估计值
在受到连续正弦信号干扰时,单级直线倒立摆摆杆夹角响应曲线如图4所示。由图4可以看出,在所受干扰相同的情况下,摆杆与垂直向上方向的夹角,在反步控制器控制时,单级直线倒立摆受干扰的影响较大,摆杆摆角不能渐近稳定在平衡位置,出现振荡。基于干扰观测器的抗干扰反步控制器控制时,控制器对连续正弦信号干扰有很好的抑制效果,系统没有超调,摆杆大约在仿真开始后的第2 s摆动到平衡位置,基本达到稳定状态。
在受到连续正弦信号干扰时,单级直线倒立摆小车位置响应曲线如图5所示。由图5中可以看出,为保证摆杆的平衡,小车来回运动,这是由单级直线倒立摆系统的欠驱动性决定,但基于干扰观测器的抗干扰反步控制器控制时,要比基本的反步控制器振荡幅度小。因此,基于干扰观测器的抗干扰反步控制方法,对连续正弦信号干扰的抑制有效。
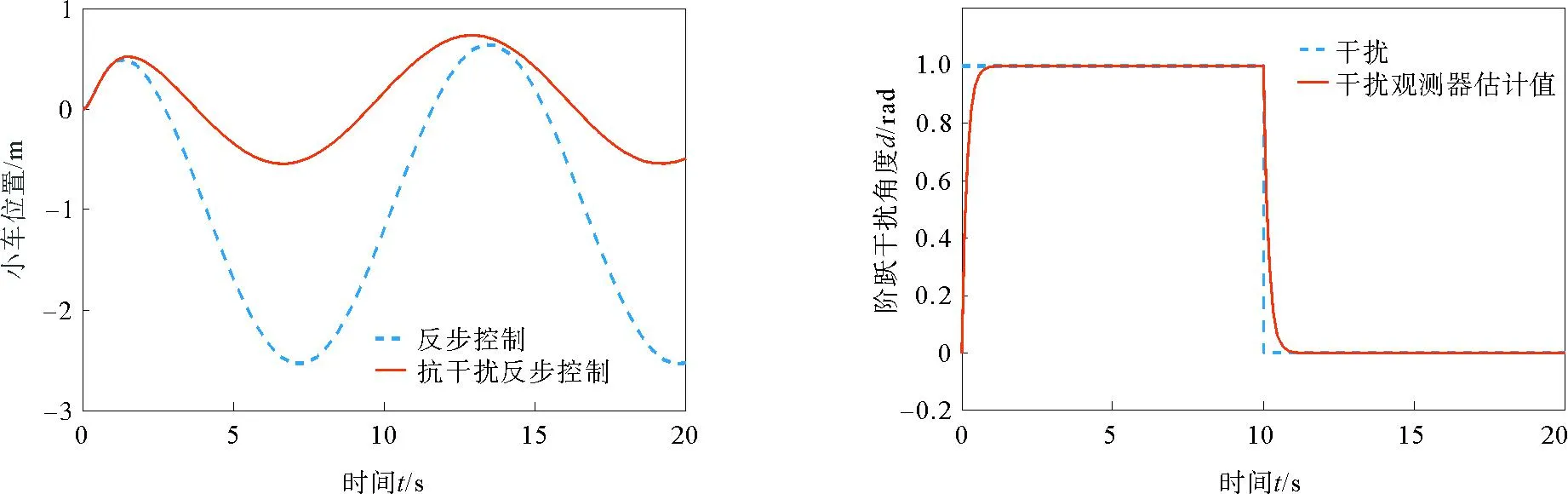
图5 单级直线倒立摆小车位置响应曲线
4.2 单级直线倒立摆受到阶跃干扰信号时的控制效果
在受到瞬时阶跃信号干扰时,单级直线倒立摆受到的瞬时阶跃干扰信号d在第10 s幅值由1阶跃为0,干扰与干扰观测器估计值如图6所示。由图6可以看出,干扰观测器能够在有限时间内有效估计瞬时阶跃干扰信号。
在受到瞬时阶跃信号干扰时,单级直线倒立摆摆杆角度响应曲线如图7所示。由图7可以看出,在所受干扰相同的情况下,摆杆与垂直向上方向的夹角,在反步控制器控制时,单级直线倒立摆受干扰的影响较大,幅值为1时的干扰,摆杆摆角较大幅度地偏离了平衡位置,出现了持续的0.05 rad的误差,待干扰阶跃为0后,经过控制器的控制,重新回到稳定状态。基于干扰观测器的抗干扰反步控制器控制时,控制器对瞬时阶跃信号干扰有很好的抑制效果,较平滑地处在平衡位置的稳定状态,只在瞬时阶跃时,摆杆摆角有较小幅度的变化。

图7 单级直线倒立摆摆杆角度响应曲线
在受到瞬时阶跃信号干扰时,单级直线倒立摆小车位置响应曲线如图8所示。由图8可以看出,在受到的瞬时阶跃干扰信号相同的情况下,单级直线倒立摆系统在反步控制器控制时,小车运动的幅度较大才能使摆杆重新平衡,基于干扰观测器的抗干扰反步控制器控制时,为使摆杆重新平衡,小车运动的幅度比基本的反步控制器控制时幅度小约3.5 m,效果明显提高。综上所述,基于干扰观测器的抗干扰反步控制方法,对瞬时阶跃信号干扰的抑制是有效的。
5 结束语
为了提高单级直线倒立摆控制系统的鲁棒性和抗干扰性能,本文提出了基于干扰观测器的倒立摆抗干扰反步控制方法。仿真结果表明,相对于反步控制,该算法对连续正弦信号干扰或瞬时阶跃信号干扰有效,具有较强的抗干扰能力。本研究设计了干扰观测器对外界干扰实时估计,将干扰的估计值反馈给控制器产生抑制干扰的补偿量,抑制干扰。考虑到在实际环境中外界干扰对倒立摆系统的影响,具有一定的理论研究和实际应用价值。为进一步提高倒立摆的抗干扰性能,对不同类型干扰的分析是接下来的研究方向。
