基于OpenCL的腐蚀膨胀算法的并行优化
2024-01-03王文善张维忠
王文善, 张维忠, 李 强
(青岛大学计算机科学技术学院, 山东 青岛 266071)
传统的腐蚀膨胀算法一般是在CPU运行的串行算法,算法中存在大量的相似运算和冗余运算,算法效率低,随着图像处理技术的不断发展,图像和结构元素不断增大,渐渐无法满足形态学实时图像处理的要求。当前研究的热点是提高图像处理算法的效率、准确性和通用性,许多学者对腐蚀膨胀算法进行了改进研究。基于SE去组合的快速无失速低复杂度体系结构方法[1]对于结构元素进行了优化,降低了算法的计算复杂性,但其通用性较低。通过积累结构元件内每个像素的PPI指数来找到最纯净的像素[2],提高了算法的自动化程度和效果,然而算法的处理速度并没有提高。二维结构元素的1-D分解和点对分解[3]可提高计算速度,但仅针对凸集等紧1-D分解元效果较好,因此通用性不强。1-D 分解元的结构元素构造的点对分解算法[4-6],计算速度快但不适合于灰度图;对于区域采用线段表示法的方法[7]算法的准确性有所提高,但这种算法适宜于连续施行腐蚀膨胀操作的情况;减少相邻像素重复区域的计算量的方法[8],本质上还是串行算法,速度提高有限;在 CUDA 平台上进行改进和并行化实现是一种有效的并行算法[9-10],只针对单一平台,通用性有限。本研究通过并行化和优化算法,提高了腐蚀膨胀算法的计算效率,并具备较好的通用性。本文提出了基于OpenCL的腐蚀膨胀快速并行算法,通过利用像素无关性和图形处理器的分层存储机制[11],优化存储结构和访存方式,以及合理划分工作组和工作项,提高算法的实现速度。同时,还提出了基于OpenCL改进的膨胀与腐蚀快速并行算法,通过存储结果在共享内存中,减少计算冗余,提高效率,显著提高了腐蚀膨胀算法的效率。
1 图像的腐蚀膨胀算法
1.1 腐蚀原理
腐蚀是求局部最小值,即计算结构元素在图像中所覆盖区域的像素点最小值,并把最小值赋给当前结构元素中心指定的像素[12]。设A是输入图像,B是结构元素,则结构元B平移z后的集合表示为
(B)z={c|c=b+z,b∈B}
用B对A进行灰度腐蚀表示为
A⊖B={z|(B)z⊆A}
即结构元B平移z后依然包含在集合A中所有的z的集合,又表示为
A⊖B={z|(B)z∩Ac=Ø}
其中,Ac是集合A的补集,也就是不在集合A中的其他元素。
1.2 膨胀原理

则B对A膨胀表示为
2 腐蚀膨胀并行算法
2.1 腐蚀膨胀并行算法
由腐蚀膨胀算法原理可知,传统串行算法通过双重循环遍历图像中每个像素点,双重循环遍历结构元素的每个子元素,使结构元素中心与当前像素点重合,通过乘法计算出结构元素覆盖的所有像素点的值,从中取得最小值和最大值,即腐蚀的最终结果和膨胀的最终结果,遍历整个图像,把最终结果赋值给对应像素点。串行腐蚀膨胀示意图如图1所示,若结构元素为3×3矩阵,当前元素为30,将结构元素的中心与当前元素重合,计算结构元素覆盖范围的像素点与结构元素的乘积,取最小值作为腐蚀值,最大值为膨胀值,继续循环至下一个元素21,重复当前操作,直至遍历完图像中所有像素点。
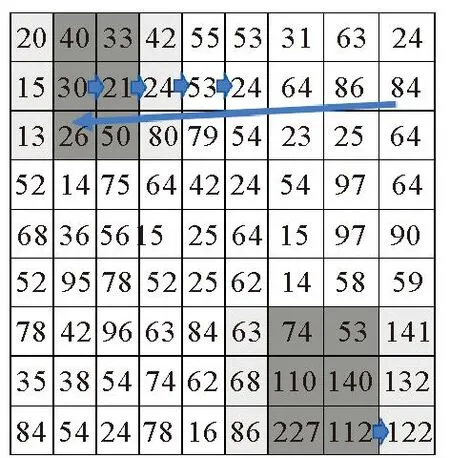
图1 串行腐蚀膨胀示意图
将以上过程看作像素独立,每个像素点只与当前结构元素覆盖范围内的像素点有关,可同时对图像中所有像素点进行计算,像素无关并行算法示意图如图2所示。第一阶段为每个像素点划分工作项,将结构元素中心对应各工作项代表的像素点,同时对每个工作项进行卷积计算;第二阶段对每个工作项中计算出的所有像素点进行排序,每个工作项中最小值为当前工作项所对应像素点腐蚀值,每个工作项中的最大值为当前工作项所对应像素点膨胀的值,将计算结果保存至本地内存。

图2 像素无关并行算法示意图
2.2 基于特定结构元素的膨胀腐蚀并行算法
由图1可以看出,当结构元素中所包含的子元素相同时,相邻2个像素点与结构元素进行卷积计算时,存在计算冗余。例如,将3×3的全1结构元素分别覆盖30和21像素点,其元素[40,30,26,33,21,50]分别计算2次,若再覆盖24像素点,则列[33,21,50]进行3次相同的计算,存在大量的计算冗余,即使采用像素无关并行算法,依然存在大量的冗余计算。因此,基于OpenCL进行改进,改进的腐蚀膨胀并行算法如图3所示,具体改进如下:

图3 改进的腐蚀膨胀并行算法
1) 假定结构元素为3×3的全1矩阵,取结构元素的某一列作为新的结构元素,则新结构元素为3×1矩阵,为每个像素点划分工作项,将新的结构元素中心与每个像素点重合。
2) 在每个工作项中同时对新的结构元素进行卷积计算,不同的是每个像素点只是对旧结构元素的一列进行卷积计算,将计算出来的每一列的最大值(膨胀)或最小值(腐蚀)保存在共享存储器中。
3) 在共享内存中,每一个工作项读取一个结构元素所覆盖的所有列的最大值或最小值,对于3×3的结构元素,工作项会读取当前像素与前后像素的共享内存的值,并计算出这些值的最大值(膨胀)或最小值(腐蚀),最终结果即为膨胀或腐蚀的结果。
该方法能够确保结构元素覆盖的每一列只计算一次,与传统的串行计算方法相比,理论上计算量减少了3倍,效率大大提高。虽然大幅度减少了计算冗余,但对结构元素有限制,因此该方法更适用于在特定结构元素中。
2.3 腐蚀膨胀并行优化
基于OpenCL的腐蚀膨胀并行算法和改进的并行算法中,以一个线程计算源图像中的一个像素点,在OpenCL中一个工作项即代表一个线程[13]。由于实验使用平台为嵌入式平台的MaLi-T860 GPU,受最大工作项大小所限,分配每个工作组中的工作项大小为16×16,若源图像分辨率为m×n,则分配工作组数目为(m/16)×(n/16)。
OpenCL内存模型如图4所示。OpenCL中将变量从主机端传入设备端,把存放在CPU内存中的变量传递到GPU的全局内存[14],即GPU的显存,把原始图像数据保存在OpenCL的Image对象及相应的采样器Sampler,通过OpenCL提供的内置函数,更方便快速地处理图像数据。算法是从全局内存中读取所需要的变量计算,将计算结果也保存其中。由于从显存中直接读写数据速度较慢,因此对内存分配进行优化,将算法中常用的变量保存在本地内存,常量保存在常量内存,将算法计算结果保存在本地内存,本地内存是每个工作组独有的内存,可被当前工作组内的所有工作项共享,起到共享内存加速的作用。
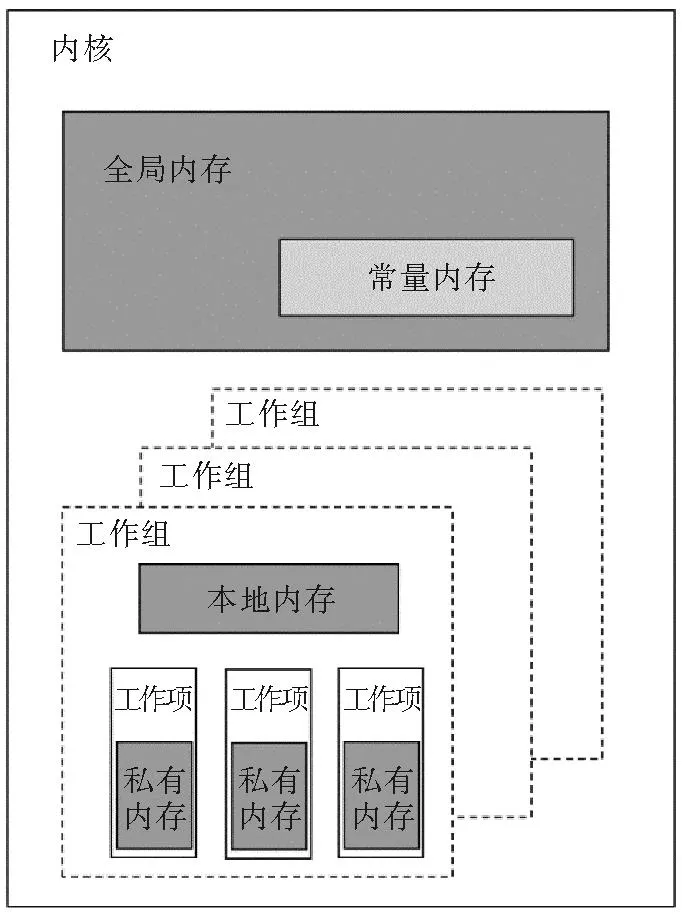
图4 OpenCL内存模型
3 实验结果与分析
3.1 实验环境
实验平台是AIO-3399C(AI)工业主板,软件环境为Ubuntu18.04 LTS,硬件环境为双Cortex-A72大核,四Cortex-A53小核处理器,ARM Mali-T860四核图形处理器(GPU),内存16G,开发环境为VSCode+OpenCL 1.2。
3.2 结果与分析
为了验证各算法的速度,比较相同结构元素、不同图像大小的各算法的加速比。固定结构元素为3×3,对比腐蚀膨胀并行算法、改进腐蚀膨胀并行算法、内存优化后腐蚀膨胀并行算法、内存优化后改进腐蚀膨胀并行算法在图像大小分别为256×256、512×512、1 024×1 024、1 024×2 048、2 048×2 048、4 096×4 096的加速比。不同图像大小的加速比如图5所示。
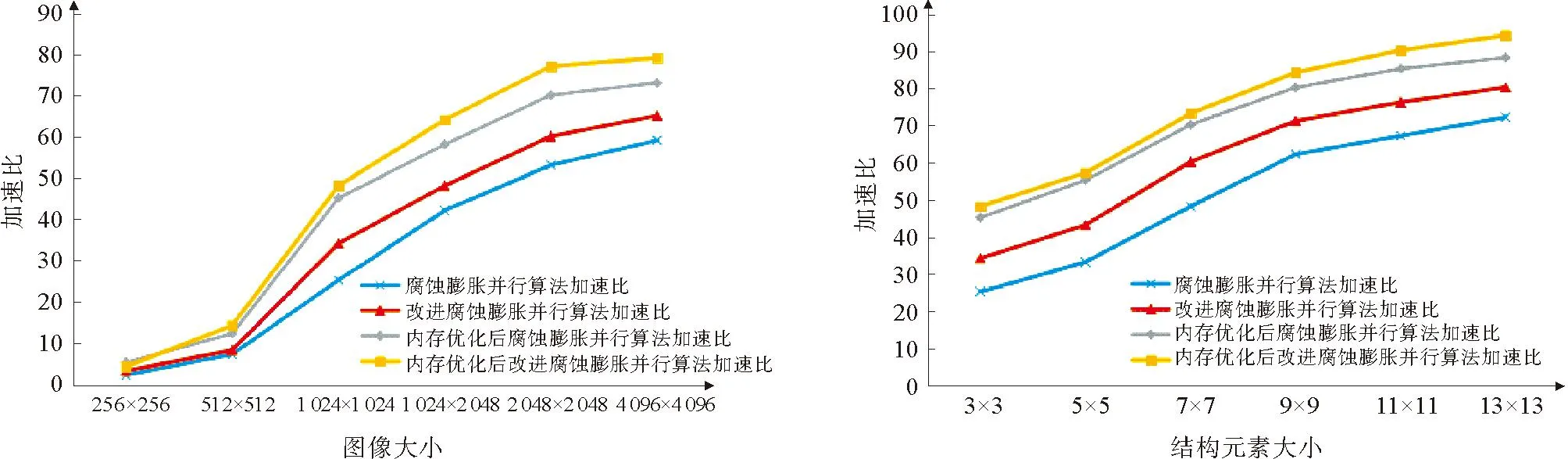
图5 不同图像大小的加速比
由图5中可以看出,在固定结构元素大小的情况下,不同并行算法均比串行算法的速度快,随着图像变大,并行算法的加速比越高,其中在特定结构元素下,改进的腐蚀膨胀并行算法加速比略高于一般的腐蚀膨胀并行算法,且与未经优化的并行算法相比,经过内存优化后的并行算法加速比有较大的提高。
不同结构元素大小的加速比如图6所示。在固定图像大小为1 024×1 024时,加速比随着结构元素大小的增大而增加,当结构元素增加到13×13时,加速比最高可以达到94左右,即使一般情况,优化过后加速比也能有88。
由图5和图6可以看出,并行算法的加速比与结构元素大小和图像大小有关,且随结构元素大小的增大或图像的增大而增大,所以对高分辨率的图像和大结构元素,腐蚀膨胀计算的加速更显著。当矩阵大小较小时,系统启动参与并行计算的工作项并不多,没有充分利用GPU中的大量计算单元,且线程之间的切换较为频繁,通信时间增加,因此加速效果并不显著。当选取高分辨率图像或大结构元素时,由于每个线程计算量的增加,GPU中每个工作项都得到充分利用,线程之间的切换减少,而GPU最大的优势就是在于大批量的相同计算,因此加速比更大。
4 结束语
本文基于腐蚀膨胀算法的特性提出了一种基于OpenCL的并行算法,利用GPU的并行计算能力和内存优化,提高算法效率。通过合理划分工作项和工作组,利用共享内存存储计算结果,并针对特定结构元素的改进,提高算法的性能,在腐蚀膨胀算法中取得更高的效率和实时性,对于需要快速处理大量图像数据的应用场景具有实际价值。下一步主要在更深入的算法优化和在其他硬件平台上的应用方面展开研究,提高算法性能,扩展其适用范围。
