真空管道高速列车系统中管道压力分布研究

陈大伟, 兰永霞, 张司薇, 高红霞, 朱克勇, 刘 猛

(1．中车青岛四方机车车辆股份有限公司工程实验室, 山东 青岛 266111; 2.北京航空航天大学航空科学与工程学院, 北京 100191)

低真空管道高温超导磁浮系统通过实现管道内的低气压创造一个低密度的运行环境,使高速列车挣脱稠密大气层的束缚,减小气动阻力与气动噪音等对列车与环境的影响,同时列车在低阻力的环境中运行也能降低能耗;而高速磁浮技术的应用能突破传统列车的轮轨黏着、蛇形失稳和弓网受流等限制,使得实现超高速的管道运输成为可能[1]。然而,磁浮列车高速行驶在密闭的管道时,又会带来许多新的气动问题。如果气压及阻塞比等参数选择不当,容易产生严重的壅塞现象,会加剧列车所受的气动阻力[2]。近年来,国内外不少学者对真空管道列车气动性能开展研究。针对列车气动阻力随阻塞比、列车运行速度和真空度之间的变化关系,陈大伟等人[3-6]基于定常可压缩Naiver-Stokes方程研究了管道大气压、阻塞比、列车运行速度对列车气动阻力的影响;米百刚等人[7-9]利用Fluent仿真软件,结合动网格相关技术研究了二维模型列车非定常气动特性;王博等人[10]研究了高温超导真空管道磁悬浮车的气动特性,建议增加旁通管道等方式来缓解管道内微气压波;M.M.J.OPGENOORD等人[11-12]分别对超级高铁(Hyperloop)无压缩机的车辆进行了外形设计与数值模拟,为管道内部飞行器提供良好的抬升力与较低的阻力,但是研究的仅仅是长度较短的飞行器;ZHOU P等人[13-15]针对二维对称模型研究了管道内部的激波与热分布,得到基于列车左右两侧对称情况下的流场等特性。基于此,本文建立了单车运行和两车交汇的真空管道交通系统模型,通过Fluent湍流模型和重叠网格划分技术,分析了真空管道高速列车系统中管道压力分布及压力场的变化规律。本研究为真空管道高速列车系统中管道压力设计提供理论依据。

1 物理模型

在传统高速列车空气动力学数值模拟中,根据列车与风的相互作用原理,采用传统风洞的方式吹风,可以等效为列车的运动,有效地节约了瞬态数值模拟的计算成本。然而,在真空管道中,列车与管道形成了一种近似收敛—扩张进气道,当空气来流与阻塞比达到特定的匹配关系时,会发生管道壅塞现象,导致风洞式来流速度受到影响,也是常规的相互作用仿真不准确的原因[11]。基于此,本文建立二维亚音速真空管道列车数值模型,结合重叠网格技术,对真空管道列车运行时引起的压力场变化进行研究。

1.1 控制方程及湍流模型

控制方程采用二维积分形式的非定常雷诺平均N-S方程[16]。

(1)

式中,V为任意控制域;W为守恒变量;F为无粘(对流)通矢量项;Fv为粘性通量;∂V为控制域的边界;n为控制域边界单位外法向矢量;Re为计算的雷诺数。

空间离散采用二阶迎风格式——通量差分分裂(Roe-FDS)格式[8],时间离散采用LU-SGS隐式时间推进格式,应用当地时间步长、残值光顺、预处理和多重网格加速收敛,对于粘性流动的数值计算,需采用湍流模型对NS方程进行封闭。本文采用的湍流模型为SSTk-ω湍流模型[17-19],该模型克服了标准k-ω湍流模型对自由流参数变化比较敏感的缺点,在近壁面附近采用k-ω湍流模型,在远离壁面的流场中采用目前广为应用的k-ε湍流模型,充分利用k-ω湍流模型对逆压梯度流动具有较高模拟精度,对湍流初始参数不敏感的优点。

1.2 几何模型、边界条件及网格划分

列车模型如图1所示。列车模型采用整车长100 m,首尾采用流线型过度,列车高4.2 m,列车底部距离管道2 m。计算域模型如图2所示。真空管道与列车的阻塞比为0.2,管道截面积为80 m2,管道的直径为5.04 m,管道长度为500 m,重叠网格最前方距离管道出口为356 m。

图1 列车模型

图2 计算域模型

重叠网格技术可有效且快速地捕捉列车周围气流的动态特性,故采用重叠网格技术实现列车运行模拟[20]。在列车周围生成重叠网格,管道由另一种网格覆盖,也就是背景网格,列车周围的重叠网格会完全嵌入背景网格,2个网格之间的信息交互通过线性插值算法完成,通过重叠网格的移动完成列车的实际运行状态,采用结构化网格对模型进行网格划分。在列车表面进行边界层的加密,利用y+=1值计算第一层网格高度为6 mm,为了保证网格有良好的过渡,设置延展率1.2,共计15层,列车表面边界层总网格高度432 mm,整体网格数量为10万,网格划分如图3所示。

图3 网格划分

管道顶部与底边均采用无滑移壁面处理[21],入口与出口边界条件采用模拟无限远管道长度的自由流边界条件,重叠网格区域运行速度对应真空管道列车运行速度。管道内部环境压力为1.01×103Pa,气体黏度满足Surtherland定律。为了更好地捕捉列车表面与管道内壁的剪切特性,湍流模型采用SSTk-ω湍流模型。耦合隐式时间步长为0.01,瞬态计算总时长为0.82 s。

2 结果及分析

2.1 真空管道内的压力分布及影响因素

根据上述模型及计算方法,考虑到不同工况下的真空管道内压力分布,网格划分如图3所示。网格划分主要包括不同的管道面积(60 m2和80 m2)、不同列车运行速度(600 km/h、800 km/h和1 000 km/h)和不同的真空管道压力(1.01×103Pa和1.01×104Pa)。不同工况下真空管道内压力变化云图如图4所示。

图4 不同工况下真空管道内压力变化云图

1) 不同的管道截面积。图4中1和2是不同截面积影响压力变化的对比。从压力云图可以看出,随着管道截面积的减小,阻塞比增大,管道的壅塞现象更明显,壅塞影响区域更大,同时列车头部1的压力比2的压力小,截面积减小,导致管内的压力升高。

2) 不同的列车运行速度。图4中1、3和4是不同速度影响压力变化的对比。从压力云图可以看出,随着列车运行速度的增加,列车头部的管道内压力逐渐升高,同时尾部的激波现象越来越明显,运行速度为600 km/h的工况下,已经看不到激波的产生,列车尾部压力变化平缓。

3) 不同的管道真空度。图4中1和5是不同管道真空度影响压力变化的对比。从压力云图可以看出,保持列车运行速度和管道截面积不变的情况下,管道真空度的改变对整体的管道压力分布没有太大影响,包括壅塞的影响区域以及尾部的激波形状。

2.2 列车表面的压力分布

通过CFD计算,提取不同位置列车表面压力分布情况,列车运行速度和管道截面积对列车表面压力分布的影响如图5所示。

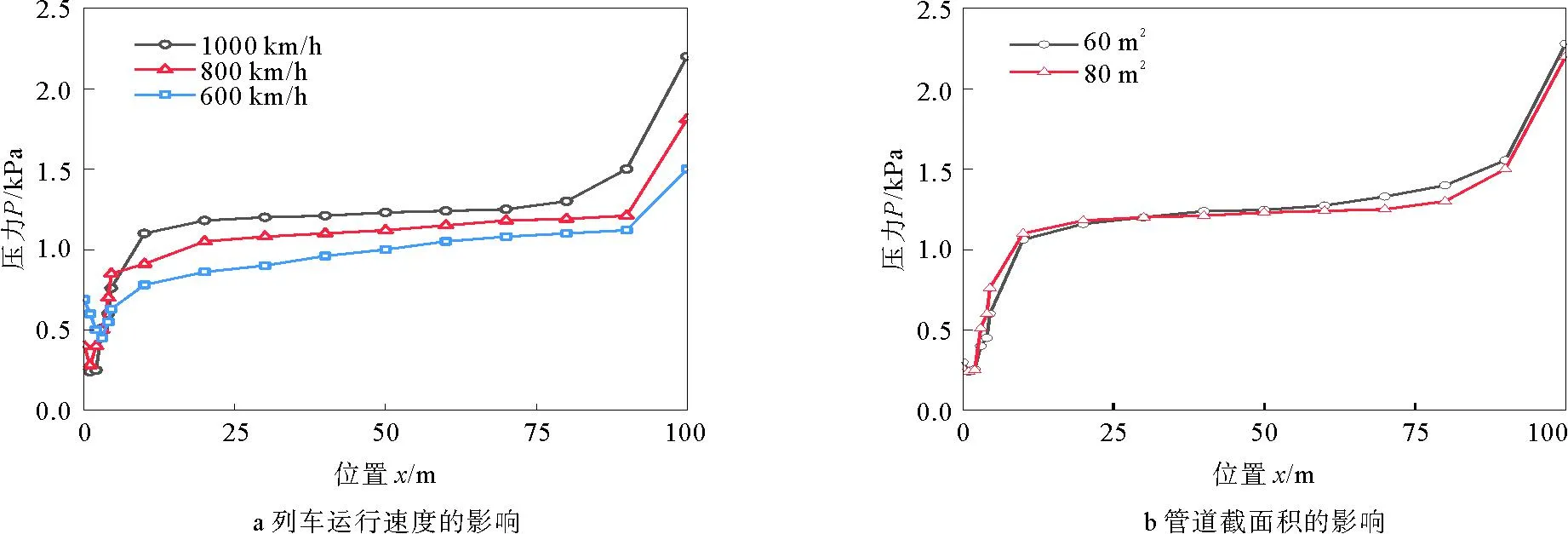
图5 列车运行速度和管道截面积对列车表面压力分布的影响

1) 不同的列车运行速度。随着列车运行速度的增加,列车表面的压力整体逐渐增大,且不同速度下的压力沿列车表面的分布情况相同,头部压力高,尾部压力低,与其它2个速度相比,列车运行速度为600 km/h时,尾部压力变化更缓和,没有压力的突降,这是因为未产生激波。

2) 不同的管道截面积。由图5(b)可以看出,管道截面积的变化对列车表面的压力分布影响不大,因此可以不用考虑对压力的变化带来的影响。

3) 不同的管道真空度。由于不同管内压力下的列车的表面压力分布比例变化太大,因此对于不同真空的列车表面压力变化情况单独考虑,观察其规律变化情况。管道真空度对列车表面压力分布的影响如图6所示。由图6可以看出,不同压力对整体列车表面的分布情况基本没有太大改变。

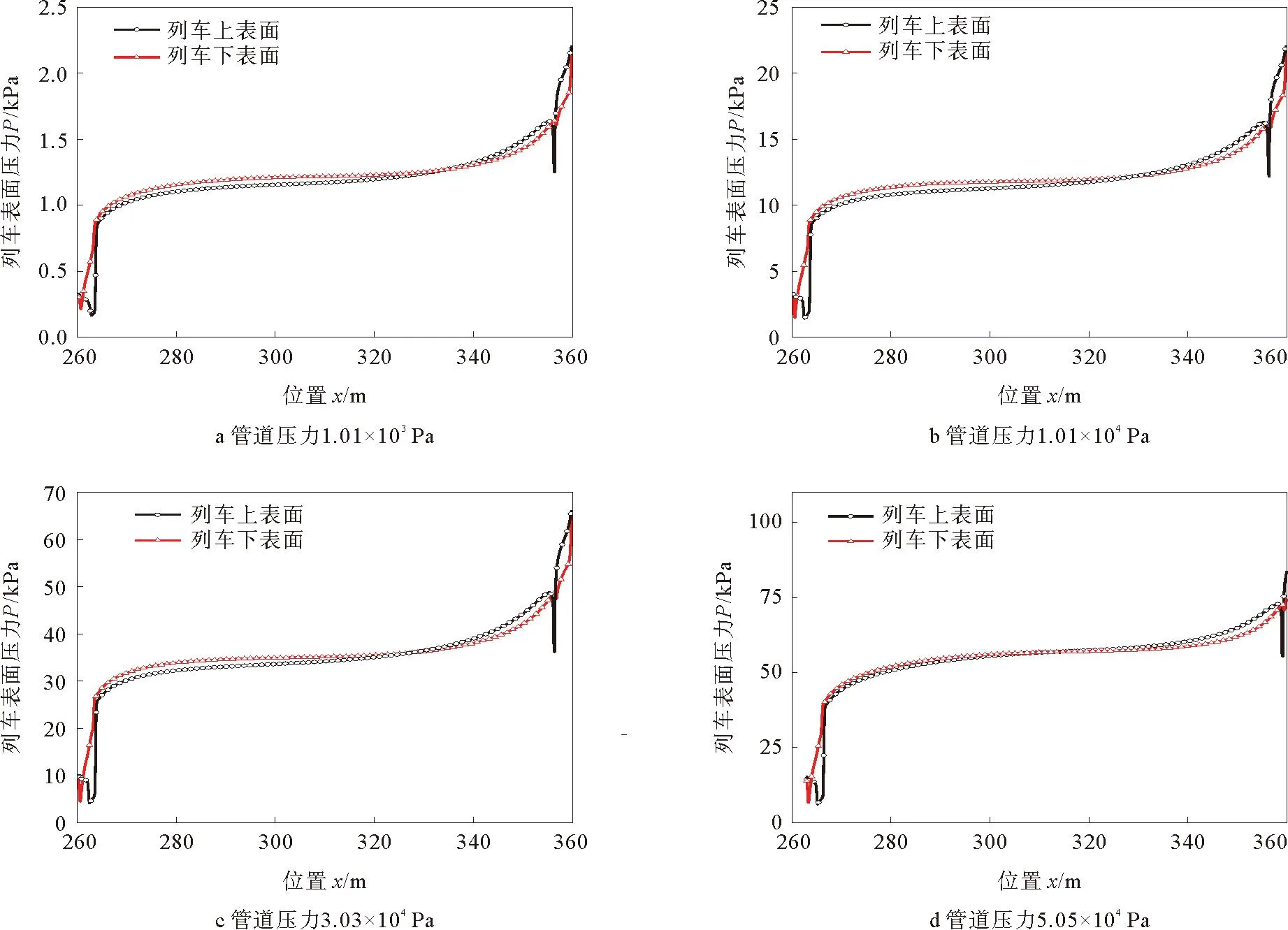
图6 管道真空度对列车表面压力分布的影响

2.3 低真空管道列车双车交汇仿真分析

1) 双车交汇模型。两车交汇时主要面对俯视视角,因此,列车外形采用宽度作为横向长度,具体尺寸为管道截面积100 m2,总长500 m,2辆列车总长127.5 m,列车宽3.7 m,双车交汇几何模型如图7所示。控制方程、湍流模型、边界条件和网格划分与单车运行时基本一致,重叠网格区域运行速度对应真空管道列车运行速度,左侧的车向右行驶,右侧车向左行驶,双车交会。双车交汇网格划分如图8所示。

图7 双车交汇几何模型

图8 双车交汇网格划分

2) 双车交汇仿真分析。双车交汇压力场云图如图9所示。由图9可以看出,随着两车交汇,列车头部的压力先升高再降低,两车交汇时达到最大值。这是由于两车前方的高压气体相互挤压的原因,这部分空气由于管道的尺寸限制,压缩在一起压力更大。

图9 双车交汇压力场云图

两车交汇时两辆列车表面压力变化情况如图10所示。

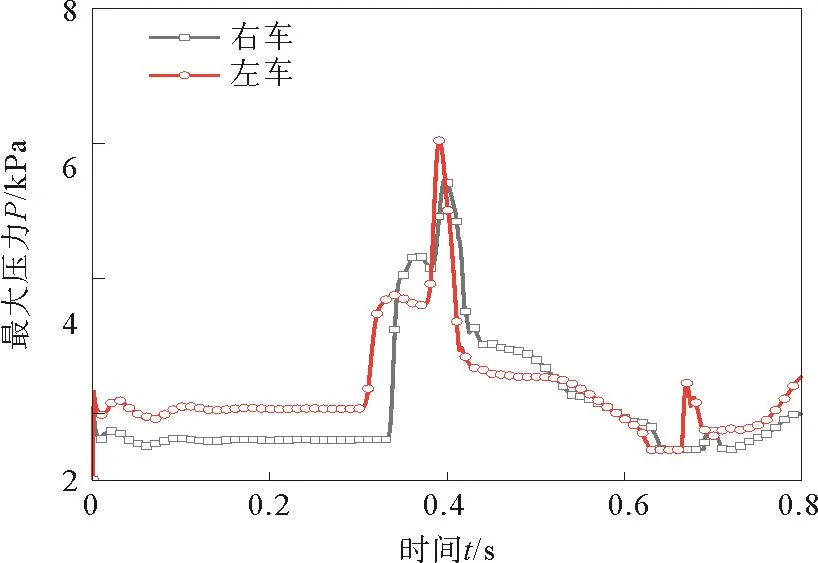
图10 两车交汇时两辆列车表面最大压力变化情况

由图10可以看出,两车交汇时,真空管道内压力分布变化较大,压力变化率最大达到了110 kPa/s,远远超过了限定标准值,管道内的压力波动也会影响到列车内部的压力波动,影响乘客的生命安全。因此,双线运行管道中的列车需要对车厢内的压力调节系统进行额外设计,考虑两车交汇时真空管道内压力剧烈变化的情况,减小会车时车厢内的压力波动。

3 结束语

本文采用Fluent湍流模型和重叠网格划分技术,研究了高速列车运行对真空管道压力分布的变化规律,探讨了列车运行速度、管道阻塞比和管道真空度对真空管道压力分布的影响。列车运行速度和阻塞比对真空管道内压力分布影响较大,管道真空度影响较小;列车运行速度对列车表面压力分布影响较大,阻塞比和管道真空度影响较小;两车交汇时,真空管道内压力分布变化较大,最大达到110 kPa/s。影响列车内的压力调节系统,需要在设计时考虑两车交汇时真空管道内压力的剧烈变化情况。真空管道高速列车系统中管道压力分布影响列车运行气动阻力、气动噪声等问题,同时对于高速列车内部的压力控制也有重要影响。本研究为真空管道高速列车系统中管道压力设计提供理论指导。