SS 型PT 对称磁耦合无线电能传输系统特性分析

胡 鹏，杨庆胜，王 宁，宁 艳，曹佳佳，徐 妍

（江苏方天电力技术有限公司，南京 211102）

磁耦合无线电能传输MC-WPT（magnetic coupling wireless power transfer）技术基于磁场耦合原理实现电能从电源侧到用电侧的无电气连接传输，具有安全、可靠、灵活、便捷等优势，已广泛应用于消费电子、家用电器、电动汽车等领域[1-4]。然而，传统的MC-WPT 系统具有较差的位置鲁棒性[5-8]，必须增加相应的主动调谐，如频率跟踪或参数调整，以在传输距离或传输方向变化的情况下实现高效的能量传输[9-12]。

文献[13-15]表明，将宇称时间PT（parity time）对称特性应用于MC-WPT 系统可以有效地提高其位置鲁棒性。在该方案中，系统自动调整工作频率以保持有效的功率传输。基于量子理论的宇称时间对称性概念很难理解，尤其是对电气工程师来说。目前的研究主要是基于相关特性对PT 对称的参数调节进行分析，对系统的阻抗特性、工作模式分析得较少。运行模式和电气参数之间没有分析关系来指导实际的系统设计。更重要的是，基于运算放大器OA（operational amplifier）的PT 对称MC-WPT 系统只能用于PP 拓扑[13]，而不能用于常见的SS 拓扑，这极大地限制了该技术的应用领域。

鉴于此，本文从电路分析的角度出发，深入分析SS 拓扑系统的工作原理及系统特性，给出系统结构以及运行模式和系统参数之间的数学关系，证实PT 对称工作机制就是实本征态机制。在此基础上，深入分析不同本征态下的阻抗特性和能效特性，为系统设计提供相应的理论准则。

1 系统建模及特性分析

1.1 系统建模

SS 拓扑PT 对称MC-WPT 系统等效电路如图1所示，其中：-Rs1R/Rs2形成负电阻并为系统提供增益；Rp1、L1分别为发射线圈的电阻和自感；Rp2、L2分别为接收线圈的电阻和自感；M 为互感；C1、u1分别为发射机的补偿电容和相应的电容器电压；C2、u2分别为接收器的补偿电容和相应的电容器电压；i1、i2分别为指示发射器和接收器中的电流；RL为负载。

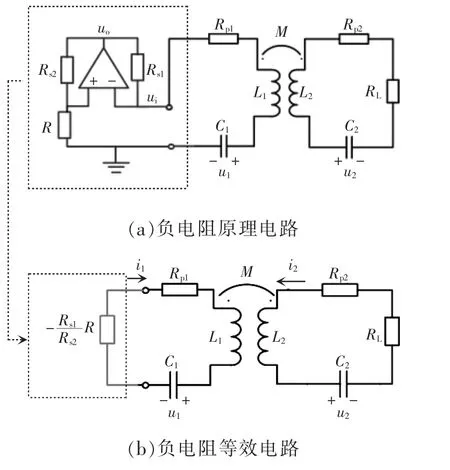
图1 SS 拓扑PT 对称MC-WPT 系统等效电路Fig.1 Equivalent circuit of SS topological PT symmetrical MC-WPT system

根据基尔霍夫电压定律，图1 所示系统的数学模型可表示为

式中，Rg=-Rs1R/Rs2。

定义U=[u1，u2]T表示系统的电容电压向量，建立系统的本征方程，并定义L、C、R 分别为系统的电感、电容、电阻矩阵，表达式为

则式（1）可转化为

解此二阶齐次微分方程，得通解：U=U0ejλt，其中U0为常数，λ 为本征值，系统的本征值λ=jδ±ω，虚部δ 表征系统的衰减特性，实部ω 表征系统自由响应的振荡频率。当δ＞0 时，系统响应为衰减振荡；当δ＜0 时，系统响应为发散振荡；当δ=0 时，系统响应为等幅振荡。对于不存在外部激励的自由响应系统而言，无论自由响应是发散振荡还是衰减振荡，系统都是不稳定的。当且仅当自由响应为等幅振荡，即δ=0 时，系统才能稳定运行。

为了便于后续分析，将系统本征值为实数（即虚部δ=0，本征值为λ=±ω）的状态称之为“实本征态”。图1 所示的MC-WPT 系统只能在实本征态模式下稳定运行。因此，PT 对称MC-WPT 系统实质上就是工作在实本征态模式。

1.2 阻抗特性分析

将接收端阻抗用一个集中参数阻抗Z2表示，根据PT 对称无线电能传输的要求，系统的发射端线圈与接收端线圈应绕制一致，参数相同，即L1=L2=L，C1=C2=C，Rp1=Rp2=Rp，则Z2表示为

由电路原理可得，接收端对发射端的负载效应可以用一个反射阻抗表示。该反射阻抗与原副边耦合系数和工作频率有关，即

将式（4）代入式（5），则可得反射阻抗Zr2为

对从原边电源端口看出去的输入阻抗进行建模，此输入阻抗Zin为

将输入阻抗Zin分解为实部与虚部，即可得等效输入电阻Rin与等效输入电抗Xin为

输入阻抗Zin的实部Re Zin代表实际功率传输的负载电阻，而虚部Im Zin指示无功功率流的负载电抗。为了使系统工作在实本征态，系统应在输入阻抗Zin的零相位角频率下运行。在这些频率下，输入端口看进去的负载电抗为0，消除了无功功率流。为了实现此目标，应使等效输入电抗为0，即

将式（9）代入式（10），可得6 个解，即

其中，后三组解为负值，为无效解，舍去，故输入阻抗Zin的零相位角频率有3 个。将这3 个角频率转换为频率，有

用发射端线圈与接收端线圈自感L与耦合系数k 表示发射端线圈与接收端线圈间的互感值M，即

将式（20）代入式（17）～式（19），可得零相位工作频率随耦合系数k 的变化曲线，如图2 所示，图中3 条曲线分别代表零相位工作频率f0、f1、f2时工作频率随耦合系数k 的变化。

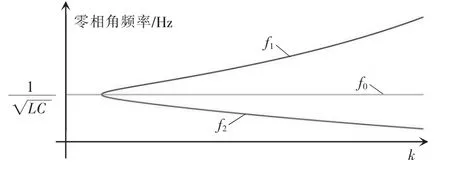
图2 SS 型系统零相角工作频率随耦合系数k 的变化Fig.2 Variation of zero-phase angle operating frequency of SS topological system with coupling coefficient k

由图2 可见，无论两线圈之间的耦合系数k 如何变化，f0始终不变，为一定值，故将此频率称为“定频”，并将系统工作在此频率下的状态称为工作在“定频实本征态”；而f1及f2会随两线圈之间的耦合系数k 不断变化，故将这2 个频率称为“浮频”，并将系统工作在此频率下的状态称为工作在“浮频实本征态”。

将f0代入等效输入电阻Rin的表达式，得

将f1及f2代入等效输入电阻Rin的表达式，得

系统Rin随k 的变化曲线如图3 所示。其中3条曲线分别表示系统工作在频率f0、f1及f2下的情形。显而易见，在定频f0下，系统输入阻抗与耦合系数呈正相关，故SS 型系统在频率f0下不具有高线圈位移鲁棒性；而在浮频f1或f2下，系统输入电阻仅与负载与线圈内阻有关，不随耦合系数变化，故SS 型系统在浮频f1或f2下具有高线圈位移鲁棒性。

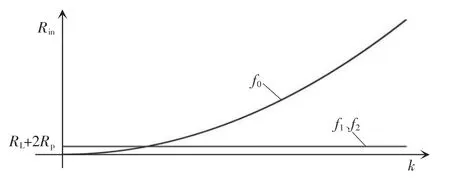
图3 SS 型系统输入电阻随耦合系数k 的变化Fig.3 Variation of input resistance of SS topological system with coupling coefficient k

1.3 SS 拓扑PT 对称系统特性分析

基于式（1），可得SS 拓扑PT 对称系统的传输效率η与传输功率Pout分别为

将f0、f1及f2代入式（23）、式（24）及式（25），可得各本征模态下系统的能效为

式（26）和式（27）表明，SS 型系统工作在定频f0下，传输效率随耦合系数k 减小而减小，输出功率随耦合系数k 减小而增大；输出功率随工作频率f变化；而在浮频下，传输效率及输出功率为一定值，不随耦合系数k 变化，亦不随工作频率f 变化。

2 仿真验证

上述分析都是基于集总参数进行分析，而对于实际系统，系统的互感变化是由于接收端距离或者方位变化导致的，因此以实际系统为例，先基于COMSOL 求取，得到互感关于距离的函数，进而将互感代入系统的能效方程中进行特性验证。磁耦合机构为平面螺旋线圈，实物如图4 所示，对应的电参数如表1 所示。

表1 SS 型系统电参数Tab.1 Electrical parameters of SS topological system

图4 线圈实物Fig.4 Coil specimen

两个线圈同轴共心放置，改变两线圈间距d，使用COMSOL 软件进行仿真，得到两线圈间耦合系数k与两线圈间距d 的变化关系，如图5 所示。

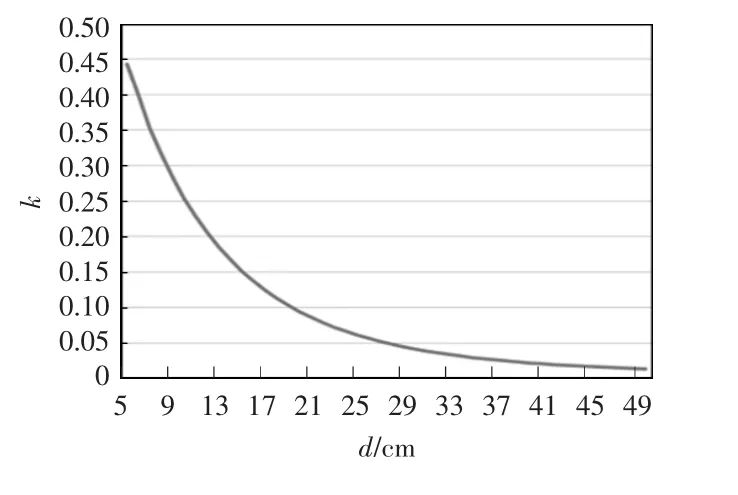
图5 L=398 μH 时线圈间耦合系数k与线圈间距d 的变化关系Fig.5 Relationship between coupling coefficient k and coil spacing d when L=398 μH

根据图5 所示的COMSOL 仿真结果，将互感作为距离的函数代入到系统的能效表达式中，进行特性数值仿真验证。首先，计算得出定频f0=84 kHz。在定频f0=84 kHz 下，依次取d=5，7，9，11，13，15，17，19，21，23 cm，根据图5 所示的COMSOL 仿真结果获得对应的耦合系数k 进行仿真，得到输入功率与输出功率。类似地，求出浮频并在浮频下依次取d=5，7，9，11，13，15，17，19，21，23 cm，得到不同耦合系数下的浮频数值及输入功率与输出功率，不同工作模式下系统的能效仿真曲线如图6 和图7所示。

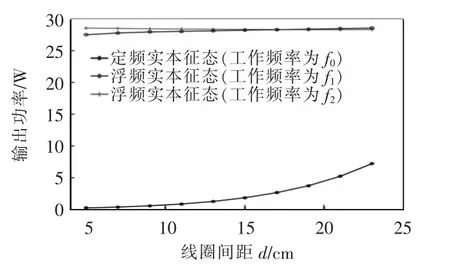
图6 不同工作模式下的输出功率仿真对比Fig.6 Simulation comparison of output power in different working modes

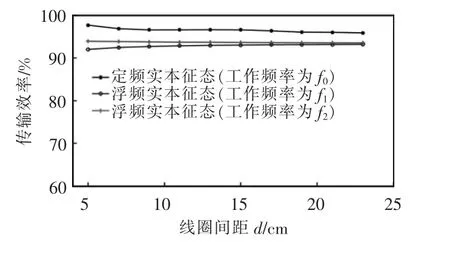
图7 不同工作模式下的传输效率仿真对比Fig.7 Simulation comparison of transmission efficiency in different working modes

从图6 中可以看出，当SS 型系统工作在定频下，在两线圈间距由5 cm 增大到25 cm 时，功率由1 W 增大到8 W，功率等级仅有瓦级；而当工作在浮频下，在两线圈间距由5 cm 增大到25 cm 时，输出功率基本为28 W 不变，不随两线圈间距变化而变化，且功率等级相较定频提升一个数量级。从图7 中可以看出，当SS 型系统工作在定频下，传输效率保持在较高的水平，但随线圈间距增大而下降；当SS 型系统工作在浮频下，传输效率低于定频时的3%～5%，但基本保持恒定。定频的传输效率最高，但是输出功率在近距离时非常低。在浮频有效工作范围内传输效率和输出功率均较高且保持恒定。仿真结果与理论分析一致。

3 结语

本文先对PT 对称系统进行建模，指出了PT对称MC-WPT 系统实质就是工作在实本征态模式。在此基础上，采用阻抗分析方法对SS 拓扑PT对称MC-WPT 系统进行了分析，求出了SS 拓扑的系统工作在定频实本征态和浮频实本征态下输入阻抗表达式。令该输入阻抗表达式的虚部为0，解出了SS 拓扑的系统分别工作在定频实本征态和浮频实本征态下的零相角频率表达式。最后求出了SS 补偿拓扑的系统输出功率与传输效率表达式，并进行了仿真验证，为实际系统工作模式选择提供了理论依据。