非线性铁磁谐振无线电能传输拓扑结构
2023-12-28李定珍
樊 京,李定珍,杨 旭
(南阳理工学院信息工程学院,南阳 473004)
无线电能传输技术受到科学界和产业界的广泛关注,已经应用于手机、机器人和电动汽车等领域。创新拓扑结构和改进控制算法均能显著提升无线电能传输的性能。经过多年的研究,典型的无线电能系统传输效率在理想条件下最高已经达到96%,输出既可以是恒流,也可以是恒压。拓扑结构也从最初的SS、SP 结构发展为LCL 和LCC 等三阶乃至更高阶补偿[1-8]。然而,多数文献拓扑电路的推导都是基于电路理论和拉氏变换,限定了其研究结论仅仅对线性系统有效。实际工况中,无线电能传输需要考虑至少3 个变量:耦合系数、频率、负载。研究表明[9],在线性系统条件下,仅依靠拓扑结构的设计,很难做到三者的共同优化。在动态无线电能传输过程中,当AGV 设备从一个线圈跨越到另一个线圈时,耦合系数和负载甚至频率均会大范围变化。单一拓扑补偿结构无法达到理想的性能指标,额外的控制系统(例如频率追踪)又增加了系统成本[10-12]。
线性拓扑结构的研究已经比较成熟,非线性拓扑结构的理论分析和实验验证则较为困难。非线性谐振具有显著不同于线性谐振的动力学特点,其谐振频带较宽且输出电压稳定。尽管部分研究论文[13-15]报道了非线性谐振的理论和实验结果,但实现的功率和效率仍与实际应用要求存在较大差距。为此,本文提出一种通过LCC-LCC 结构改进的非线性拓扑结构。这种结构容易驱动、线圈电流恒定且无需闭环控制;次级使用LCC 并联非线性电感。通过反复计算、选择材料并进行实验验证,本文将非线性拓扑结构的功率提升至500 W 以上,具备工业应用的可能性。
1 非线性拓扑结构原理
20 世纪70 年代,非线性铁磁谐振变压器技术被广泛应用于电视机和空调稳压[16-17]。随着电子变压器的逐渐成熟,铁磁谐振变压器退出大众市场。然而,铁磁谐振变压器具有成本低、可靠性高、能有效吸收尖峰脉冲等特点,仍然在飞机、高铁、有线电视等诸多领域得到应用。本文通过实验发现,基于铁磁谐振的非线性拓扑结构可用于高自由度的无线电能传输,其潜在优点如下:
(1)非线性谐振具备频带展宽功能,其谐振带宽是线性谐振的1.7 倍以上[18]。
(2)解决了LCC-S 拓扑结构输出电压低的问题,将LCC-LCC 的恒流输出转换为高压恒压输出。
(3)自动具备过流和过压保护功能。由于没有半导体器件参与,稳压可靠性极高且成本较低。
(4)该拓扑结构在负载和耦合系数变化的条件下,输出电压稳定性远超线性拓扑结构。
通过使用杜芬方程、相量分析法分别对其频率特性、电压特性进行理论分析。
1.1 谐振频率展宽特性
本文提出的非线性拓扑结构是在传统的LCCLCC 拓扑结构基础上,增加了一个非线性饱和电感,如图1 所示。

图1 非线性拓扑结构原理Fig.1 Schematic of nonlinear topology
为便于理解,将图1 分解为图2(a)和图2(b)。图2(a)的输出为交流恒流源,记作iS,此恒流源iS将驱动图2(b)的非线性电感L3。当L3工作于饱和区间时,电感电流iL与磁链ψ 将产生三次至高次谐波。为简化推导且不失非线性,仅考虑三次谐波,有

图2 非线性拓扑结构频带展宽原理Fig.2 Principle for band broadening of nonlinear topology
式中,a、b 为系数,系数a 相当于线性电感,系数b表示磁芯的非线性电感效应。
根据基尔霍夫电流定律,有
进而,得
根据法拉第电磁感应定律,有
假定电流源由正弦波驱动,iS=Imcos(ωt),可得非线性谐振的控制方程为
将方程式(5)的参数归一化,使用数学方式来表达,可以得到
方程式(6)为典型的时域杜芬方程,在机械振动领域已经得到广泛应用,这意味着,本文提出的非线性拓扑结构将具有杜芬谐振的一些特性。求解方程式(6)的幅频响应,可得
式中,A 为振幅。方程式(7)为杜芬方程频域解。
在给定F 的条件下,以频率ω 为横坐标,振幅A 为纵坐标,使用MATLAB 对方程式(7)绘图,得到杜芬谐振的幅频特性示意,如图3 所示。为方便对比,使用画图工具将线性系统(α=0)条件下对应的线性谐振特性整合在图中。
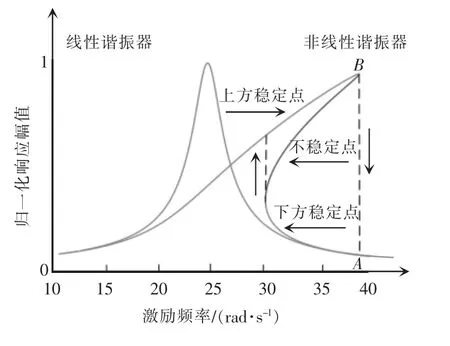
图3 杜芬谐振的幅频特性Fig.3 Amplitude-frequency characteristics of Duffin resonance
从图3 中可以观察出杜芬谐振的一些特点:
(1)线性谐振只有一个谐振点,且左右对称;杜芬谐振的频带很宽,没有明确的谐振点。
(2)杜芬谐振的谐振频率不仅与电感L 和电容C 有关,也与输入有关。
(3)在同一频率点,杜芬谐振可能存在2 个稳定工作点A 和B,其中:A 点位于线性区,B 点位于非线性区。这意味着,系统存在A 点和B 点之间的跳变。当负载过重时,系统振幅从B 点跳变到A点,从而具备过载保护功能。
1.2 输出稳压特性
杜芬方程的幅频响应特性显示,一旦进入饱和区,杜芬谐振的输出振幅斜率远小于线性谐振。这表明,杜芬谐振具有输出稳压的效果。实际磁性材料的BH 特性曲线非常复杂,不完全是三次非线性,必须使用计算机数值求解。使用相量分析中的图解法,可以快速掌握此类系统的特征。
非线性谐振的相量分析如图4 所示。图4(a)为PC95 铁氧体磁环的磁感应强度B 和相对磁导率μr随磁场强度H 的变化情况;图4(b)为电感的电流相量和电容的电流相量与输出电压相量之 间的相位关系;图4(c)为系统输出电压随输入电流的变化情况。图4(a)表明,铁氧体磁环的μr在起始阶段相对较低,当磁场强度H 增加到40 A/m时,铁氧体磁环的μr最高。当磁感应强度B 接近0.4 T 时,铁氧体磁环的μr迅速减少,表现出明显的饱和特性。图4(b)表明,当恒流源的输入电流相量很低时,电感尚未饱和,此时,流过电感的电流小,流过电容的电流大,导致,电路呈现容性状态,在相量图中的方向垂直向上(暂不考虑负载);当输入电流逐渐增加,电感两端的电压增长越来越慢,导致系统开始进入非线性谐振状态;当恒流源的输入电流相量继续增大,电感进一步饱和的方向与容性区相反,即ωL<,电路呈现感性状态。将图4(b)的3 个状态合并,取输入电流相量为横坐标,输出电压相量为纵坐标,得到图4(c)。图4(c)中:曲线1 代表线性谐振电容的特性,电容是线性的,电容两端电压的大小与输入电流成正比;曲线2 代表非线性电感的特性,电感是非线性的,电感的电流相量在增大过程中,电感逐渐饱和,两端电压不再线性增大;曲线3 为电容和电感并联后的合成特性,其中,负电流代表容性区。
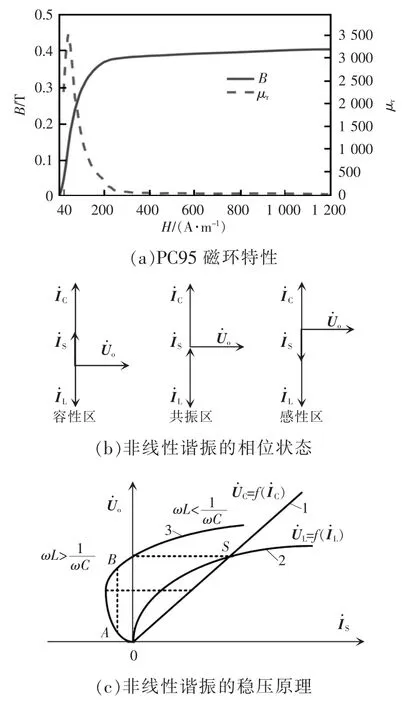
图4 非线性谐振的相量分析Fig.4 Phasor analysis of nonlinear resonance
由于非线性,曲线3 中具有A、B 两个同电流点,相当于图3 的跳变点。磁芯饱和后,输入电流的增加导致输出电压的变化很小。本文提出的非线性拓扑结构具备输出过压和过流保护功能。当系统过压时,能够快速吸收过压尖峰;当输出电流过大时,系统会从非线性区跳回线性区。综上所述,非线性拓扑结构具有很多优良的特性,可以应用在无线电能传输系统中。
2 参数设计和电路仿真
非线性谐振电路不容易获得精确的解析解,但可以利用计算机获得满足工程需要的数值时域求解。本节从非线性电感的参数设计和电路仿真结果两个方面进行研究。
2.1 参数设计
PC95 为宽温、低损耗的铁氧体材料。经过反复实验,将PC95 磁环作为优选的实验材料,其相对磁导率为3 300,饱和点为Bs=0.41 T(100 ℃)。实验选取的磁环参数为:外径DO=25 mm,内径DI=15 mm,h=13 mm,缠绕匝数N≈26。
使用是德科技精密电桥E4980A 和同惠大功率偏置电流源TH1776 对磁环进行磁饱和测量,获得非线性电感的L-i 变化,如表1 所示。从表1 可以看出,当电流i=0.05 A 时,直流电感为2 356.0 μH。由于铁氧体材料磁导率的非线性,随着电流增加,当i=0.10 A 时,直流电感增加为3 089 μH,达到电感的最大值。随后,直流电感随电流的增加而减小。当i>0.5 A 时,电感会迅速减小。
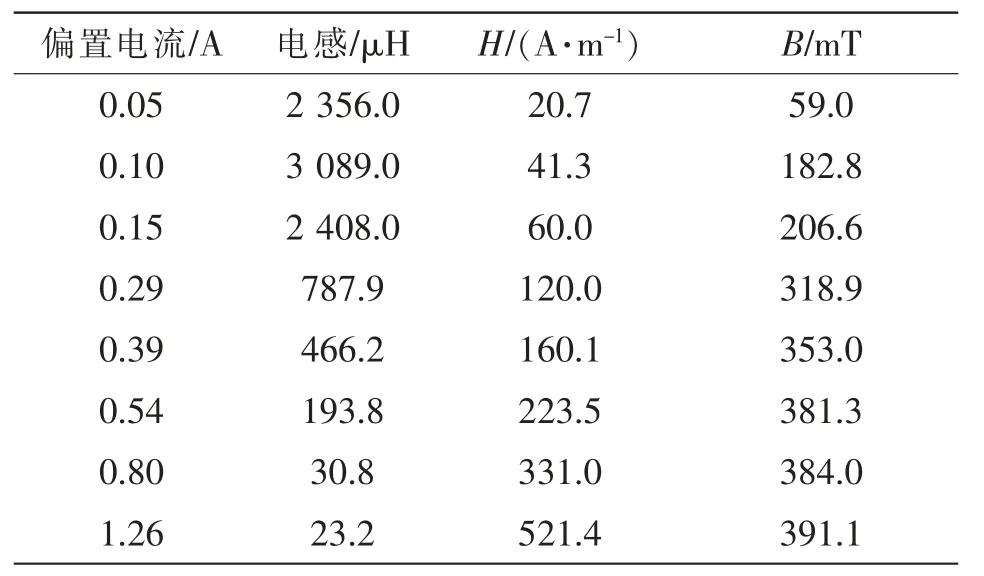
表1 PC95 磁环电感参数Tab.1 Inductance parameters of PC95 magnetic ring
2.2 电路仿真
将表1 数据导入MATLAB 作样条拟合,获得平滑且足够多的L-i 数据。导入到电路仿真软件Simplorer,作为可变电感。绘制非线性谐振仿真电路,如图5 所示。

图5 非线性谐振仿真电路Fig.5 Simulation circuit of nonlinear resonant
非线性谐振电路必须使用时域仿真。为了提高仿真精度,步长设定为0.05 μs,仿真时长设定为5 ms,发射线圈L1和接收线圈L2均为110 μH,设定工作频率为49 kHz,Lpi为55 μH。
图6 为非线性电感饱和前后输出电压及电感电流的Simplorer 仿真结果。图6(a)的耦合系数k=0.1,可以看出,电压波形基本上为正弦波,其电压峰值约为98 V。此时,非线性电感L3的电流处于临界状态,最大值为0.34 A;图6(b)的耦合系数k=0.5,可以看出,非线性电感L3的电流急剧增大,这将启动非线性电感的限压作用,导致输出电压波形远离正弦波。此时,输出电压峰值约为101 V,电流最大值约为1.4 A,非线性电感处于深度饱和状态。从仿真结果可以看出,非线性谐振电路可以在耦合系数大范围变化的条件下,保持输出电压稳定。

图6 在饱和及非饱和条件下的仿真电压、电流波形Fig.6 Simulation of voltage and current waveforms under saturated and unsaturated conditions
3 实验验证
3.1 实验装置
实验装置分为4 个模块:基于STM32G474 单片机的移相全桥PWM 波形发生模块、基于SiC 的全桥功率模块、发射谐振拓扑及发射线圈、接收谐振拓扑及接收线圈等。其中,发射线圈和接收线圈由直径为4 mm 的利兹线绕制而成,线圈的直径为400 mm,绕制的匝数为12 匝。
为了准确测量系统效率,发射端使用大功率可调直流电源IT6515 产生系统所需直流功率Pin;接收端使用1 000 W 的金属膜功率电阻作为负载,其电阻值分别为72、144、216 Ω。为了准确地测量输出功率Pout,使用了高频电压隔离探头RP1050D 和高频电流探头RP1002C。通过示波器读出电阻两端的电压电流有效值及相位差,再通过MATLAB 积分获得准确功率。实验装置的整体配置如图7 所示。

图7 实验装置的整体配置Fig.7 Integral experimental setup
3.2 实验结果
为了便于观察非线性无线电能传输系统从线性到非线性的过渡过程,使用1 000 W 功率的72 Ω金属膜电阻作为负载,直流供电电压为150 V,工作频率为49 kHz。使用2 个PC95 磁环串联,其稳压输出电压约为200 V。图8 对比展示了电感L3在非饱和及饱和情况下,系统输入电压、输入电流、输出电压和输出电流的实测波形。图8(a)显示,当发射和接收线圈距离为190 mm 时,电感L3尚未饱和,示波器测量到的输入电压和输入电流波形展示出典型的LCC 谐振拓扑的特点;图8(b)显示,当发射和接收线圈距离为120 mm 时,接收线圈电压迅速升高,系统进入非线性状态,输入电压和输入电流波形发生明显变化;图8(c)显示,发射和接收线圈距离为190 mm 时,RL两端的输出电压基本处于正弦波状态,流过饱和电感的电流仅有轻微变形;图8(d)显示,当发射和接收线圈距离为120 mm 时,RL的输出电压严重变形,从而产生稳压效果。

图8 电压电流波形在饱和及非饱和条件下的实验波形Fig.8 Experimental waveforms of voltage and current under saturated and unsaturated conditions
图9 展示了非线性无线电能传输系统的输出电压随距离和负载的变化情况。

图9 系统输出电压随距离和耦合系数的变化Fig.9 Variations of output voltage from system with distance and coupling coefficient
从图9 可以看出,当负载电阻为216 Ω、线圈耦合系数从0.50 减少到0.12 时,输出电压有效值保持在202 V 且稳定不变;当负载电阻为144 Ω、线圈耦合系数从0.50 减少到0.16 时,输出电压有效值保持在201 V 且稳定不变;当负载电阻为72 Ω、线圈耦合系数从0.50 减少到0.22 时,输出电压有效值基本保持在200 V 且稳定不变。对比不同负载曲线可以发现,系统退出非线性谐振状态时,有一个非常明显的跳跃点。跳跃现象是非线性谐振的专有特征,实验现象与本文第1 节的理论分析一致。
图10 展示了系统在不同负载条件下的效率,使用公式η=Pin/Pout计算,其中:Pin为输入的直流功率;Pout为输出功率,使用示波器电压和电流探头测量后再积分得到。从图10 中可以看出,系统最高效率为93.5%,此时,负载电阻为72 Ω,输出功率为566 W。表2 对比分析了本文提出的非线性无线电能传输系统与相关文献所提出的系统。

表2 与文献工作的对比Tab.2 Comparison with results in literature
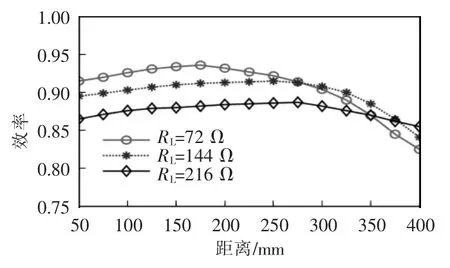
图10 在不同负载条件下的系统效率Fig.10 System efficiency under different load conditions
4 结论
本文研究了一种无线电能传输非线性拓扑结构。该结构的接收端无需主动器件的参与,具有成本低、可靠性高的特点。研究结果表明,提出的创新拓扑结构具有以下特点:
(1)非线性谐振状态下负载电阻为216 Ω 时,当线圈之间的耦合系数从0.50 下降到0.12 时,输出电压的波动不超过1%;固定耦合系数为0.22,当负载电阻从72 Ω 直至无穷大时,输出电压的波动不超过1%,实现了系统的稳压输出。
(2)相对于其他文献,实验将非线性谐振无线电能传输系统的功率提升至500 W 以上,系统最高效率超过90%,具备工程实用性。
(3)减少了闭环通信控制环节,实现了整个系统在能量层面的快速响应,可应用于动态系统。
