基于中继线圈的电动汽车静态无线充电系统抗偏移性能提升研究

葛凯梁，仇 钧，朱 海

（1.国网浙江省电力有限公司宁波供电公司,宁波 310007；2.宁波市永能电力产业投资有限公司，宁波 315000）

无线电能传输WPT（wireless power transfer）技术因其具有安全、便捷、可靠等优点，被广泛应用于电动汽车[1-4]、生物医学[5-6]、无人机[7-8]等领域，其中，在电动汽车领域应用最为广泛。然而，在电动汽车领域应用的过程中，面临的一个主要问题是，泊车过程中受人工驾驶技术或车位空间限制，无线电能传输系统原副边线圈不可避免地出现横向偏移，导致耦合程度降低，从而引起磁耦合无线电能传输系统传输功率及效率的明显下降[9-10]。

针对由于原副边线圈偏移带来的传输效率及功率下降的问题，许多文献提出了解决方案。目前国内外学者主要从闭环控制[11-12]、补偿拓扑[13-14]、耦合结构[15-19]3 个方面提升WPT 系统的抗偏移特性。文献[12]设计了一套基于调频控制和扁平螺线管的强抗偏移WPT 系统，通过闭环控制提高WPT 系统抗偏移性能的方式，需要副边反馈信号实时传输至原边，对无线通信要求高。文献[13]将SS与SP 补偿拓扑组合为SP/S 补偿拓扑，实现了较大偏移范围内输出额定功率。通过补偿拓扑改进提升WPT 系统抗偏移性能通常会增加系统的无功损耗，降低系统效率。通过改进耦合机构提升WPT 系统抗偏移性能可分为两类：一类是通过改进线圈结构[16]；一类是对中继线圈进行设计[17-20]。文献[16]提出了基于DDQ/DD 耦合机构和双路LCC/S 补偿拓扑的WPT系统，该系统具有强抗偏移性能，但设计过程复杂。

对于中继线圈设计，文献[17]提出一种可移动中继线圈的无线充电磁耦合器，在偏移情况下，使中继线圈位于最佳位置，实现了当原副边偏移距离达到外径43%时，系统效率仅下降1.8%。文献[18]提出了一种将中继线圈移至发射线圈侧的新型三线圈结构WPT 系统，该结构实现了大功率能量传输，且放置在发射侧的中继线圈能够将电源阻抗转化为一个较小的值，从而实现传输效率的提升。文献[19]提出了基于中继线圈切换的三线圈结构WPT系统，将两线圈结构与三线圈结构结合起来，解决三线圈WPT 系统近距离传输时效率较低的问题，但是文中并没有对系统的抗偏移性能进行研究。

本文提出一种基于中继线圈切换的抗偏移WPT 系统。首先，建立两线圈与三线圈WPT 系统数学模型。其次，研究横向偏移距离对两线圈与三线圈WPT 系统性能的影响，并对中继线圈半径进行优化设计。最后，进行实验验证，验证基于中继线圈切换的WPT 系统具有较强的抗偏移能力。

1 基于中继线圈的无线电能传输系统建模分析

1.1 两线圈WPT 系统模型

两线圈WPT 系统的电路如图1 所示。其中：L1、L2分别为发射线圈、接收线圈的自感，M12为它们之间的互感；C1、C2为发射线圈、接收线圈的补偿电容；R1、R2为发射线圈、接收线圈的等效内阻；RL为电阻负载；S1、S2、S3、S4为逆变器开关元件；D1、D2、D3、D4为整流器开关元件；CL为滤波电容；U 为直流输入；分别为发射线圈、接收线圈的电流相量。

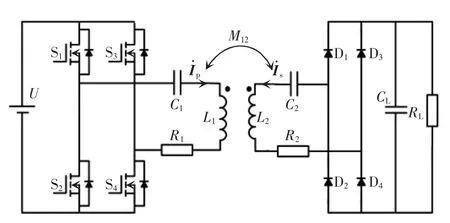
图1 两线圈WPT 系统电路Fig.1 Circuit of two-coil WPT system

为简化分析，将图1 进行等效，等效电路如图2所示。其中，为逆变电路输出电压，RLe为等效电阻负载，RLe=8RL/π2。

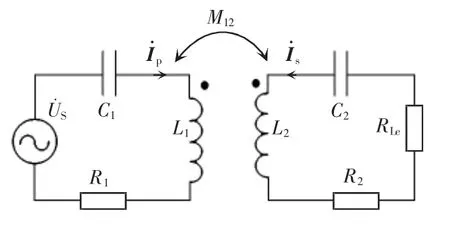
图2 两线圈WPT 系统等效电路Fig.2 Equivalent circuit of two-coil WPT system

系统工作角频率为ω，满足表达式

根据基尔霍夫定律和互感耦合理论，可得两线圈WPT 系统各线圈的回路方程为

式中，Z1、Z2分别为发射线圈、接收线圈的回路阻抗，可具体表示为

由式（1）～式（3）可求得线圈电流表达式为

设两线圈结构WPT 系统的输入功率为Pi2，则其输出功率P2与传输效率η2的表达式为

1.2 三线圈WPT 系统模型

在两线圈结构WPT 系统的发射线圈侧加入一个中继线圈，构成了三线圈结构WPT 系统，其等效电路如图3 所示。图中：Lr、Cr、Rr分别为中继线圈的自感、补偿电容及等效电阻；M1r、M2r分别为发射线圈与中继线圈之间的互感、接收线圈与中继线圈之间的互感分别为发射、中继、接收线圈的电流相量。

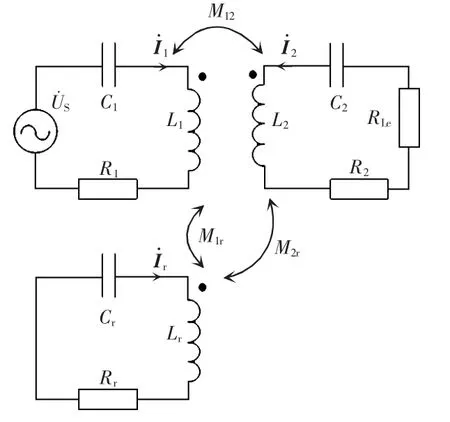
图3 三线圈WPT 系统等效电路Fig.3 Equivalent circuit of three-coil WPT system

根据基尔霍夫定律和互感耦合理论，可得三线圈WPT 系统各线圈回路方程为

式中，Zr为中继线圈的回路阻抗，具体表达式为

根据式（7）进一步推导，可得三线圈电流表达式为

设三线圈结构WPT 系统的输入功率为Pi3，则其输出功率P3与传输效率η3的表达式为

2 基于中继线圈的WPT 系统抗偏移性能研究

2.1 线圈互感仿真分析

在ANSYS MAXWELL 仿真软件中搭建线圈仿真模型，如图4 所示。发射线圈与接收线圈半径均为10 cm，线圈匝数均为20；中继线圈半径为15 cm，线圈匝数为10，且发射、中继线圈与接收线圈的距离为5 cm。当发射线圈与接收线圈发生横向偏移时，各线圈之间的互感变化情况如图5 所示。

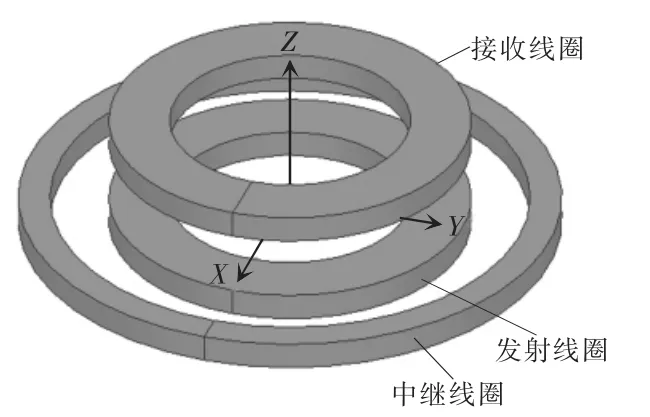
图4 ANSYS MAXWELL 仿真模型示意Fig.4 Schematic of ANSYS MAXWELL simulation model

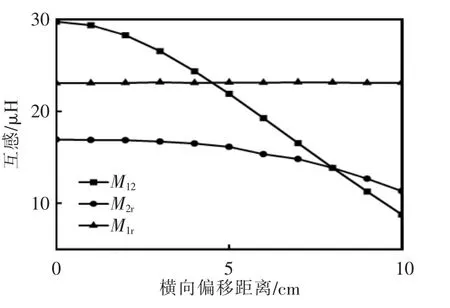
图5 各线圈间互感随横向偏移距离变化的曲线Fig.5 Curves of mutual inductance between each coil versus transverse misalignment

从图5 中可以看出，中继线圈与接收线圈之间的互感M2r在偏移距离小于5 cm 时几乎维持在16 μH，当偏移距离由5 cm 增加至10 cm 时互感M2r缓慢下降至11 μH；随着偏移距离由0 cm增加至10 cm，发射线圈与接收线圈的互感M12由29 μH 快速下降至9 μH。在发射线圈与接收线圈产生横向偏移时，发射线圈与中继线圈的相对位置未发生改变，因此发射线圈与中继线圈之间的互感M1r几乎维持在23 μH。

2.2 线圈偏移对系统性能影响研究

由上述分析可知，当发射线圈与接收线圈的横向偏移距离增加时，中继线圈与接收线圈之间的互感M2r及发射线圈与接收线圈之间的互感M12都会随之改变。由两线圈与三线圈的功率及效率表达式可以看出，线圈间互感的变化会影响系统的输出功率及传输效率。

取ω=2π×85 000 rad/s，R1=R2=0.75 Ω，Rr=0.5 Ω，RL=20 Ω，Po=20 W，可根据式（6）与式（13）绘制出两线圈与三线圈传输效率随横向偏移距离变化的曲线，如图6 所示。

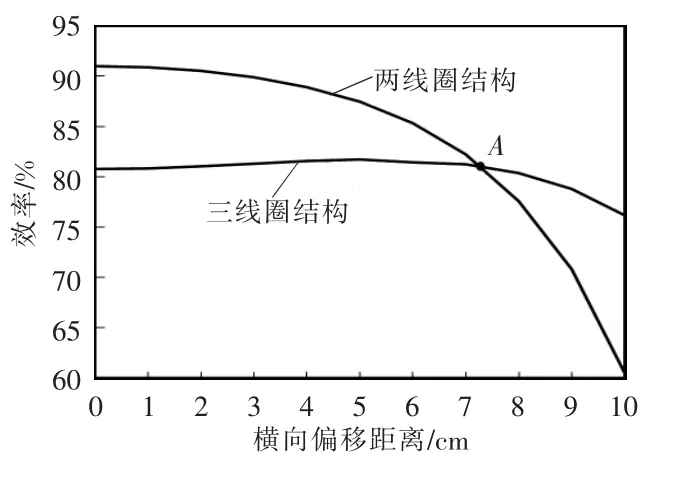
图6 两/三线圈结构效率随横向偏移距离变化的曲线Fig.6 Curves of efficiency of two-and three-coil structures against transverse misalignment

由图6 可以看出，随着横向偏移距离由0 cm增加至10 cm，两线圈结构WPT 系统的传输效率由91.0%降至60.5%，且下降速度逐渐增加；当横向偏移距离由0 cm 增加至7 cm 时，三线圈结构WPT系统效率由80.7%上升至81.2%；当横向偏移距离由7 cm 增加至10 cm 时，三线圈结构WPT 系统的效率开始缓慢下降至76%。当发射线圈与接收线圈的偏移距离小于A 点对应的偏移距离时，两线圈结构WPT 系统传输效率更高，而当偏移距离大于A点对应的偏移距离时，三线圈结构WPT 系统传输效率更高。因此，在中继线圈回路加入一个开关K，其等效电路如图7 所示。将A 点作为切换点，当横向偏移距离小于A 点对应的横向偏移距离时，开关K 断开，系统以两线圈结构工作；当横向偏移距离大于A 点对应的横向偏移距离时，开关K闭合，系统以三线圈结构工作。这样可以保证系统在任何横向偏移距离的情况下，都能有较高的效率。

图7 基于中继线圈切换的三线圈WPT 系统等效电路Fig.7 Equivalent circuit of three-coil WPT system based on relay coil switching

2.3 中继线圈结构优化

中继线圈的尺寸对抗偏移性能的影响至关重要。在发射与接收线圈半径为10 cm、匝数为20，且中继线圈匝数固定为10 的条件下，当中继线圈半径变化时，中继线圈与接收线圈的互感随横向偏移距离的变化曲线如图8 所示。

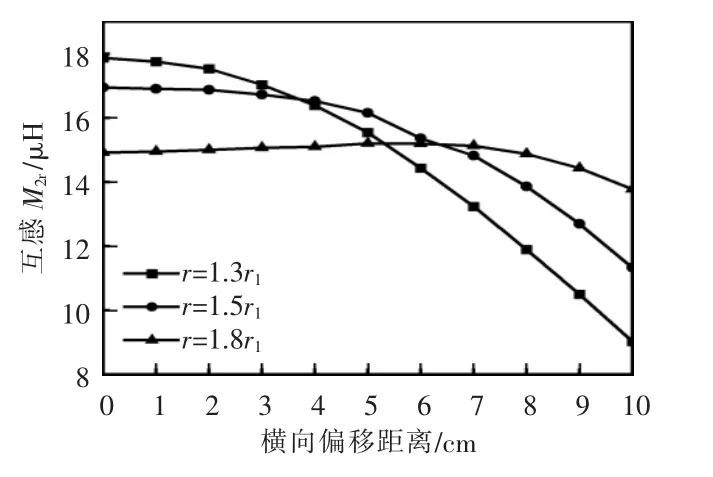
图8 不同尺寸中继线圈与接收线圈互感变化曲线Fig.8 Curves of mutual inductance between relay coils of different sizes and receiving coil

图中，r1为发射线圈半径，r 为中继线圈半径。当中继线圈半径为1.3 倍发射线圈半径时，中继线圈与接收线圈的互感M2r随横向偏移距离的增加急剧下降；当中继线圈半径为1.5 倍发射线圈半径时，M2r随横向偏移距离的增加先保持平稳后缓慢下降；当中继线圈半径为1.8 倍发射线圈半径时，M2r随横向偏移距离的增加先保持平稳后略微上升再缓慢下降。

由横向偏移距离带来的互感变化进而引起效率变化的曲线，如图9 所示。当中继线圈半径为1.3 倍发射线圈半径时，切换点A1位于横向偏移距离8 cm 处，系统效率为77.7%。随着横向偏移距离增加至10 cm，系统效率降低至69.4%。当中继线圈半径为1.5 倍发射线圈半径时，切换点A2位于横向偏移距离7 cm 处，效率为81%。随着横向偏移距离增加至10 cm，系统效率降低至76.2%。当中继线圈半径为1.8 倍发射线圈半径时，切换点A3位于横向偏移距离7.5 cm 处，效率为79.8%。随着横向偏移距离增加至10 cm，系统效率略微上升后缓慢降至79.4%。由此可见，当中继线圈半径小于1.5 倍发射线圈半径时，切换点右移，在整个偏移范围内系统传输效率较低。当中继线圈半径大于1.5 倍发射线圈半径时，切换点右移，两/三线圈结构效率曲线在切换点处存在极小值，且占用空间较大。综合考虑以上因素，选择中继线圈半径为1.5 倍发射线圈半径。

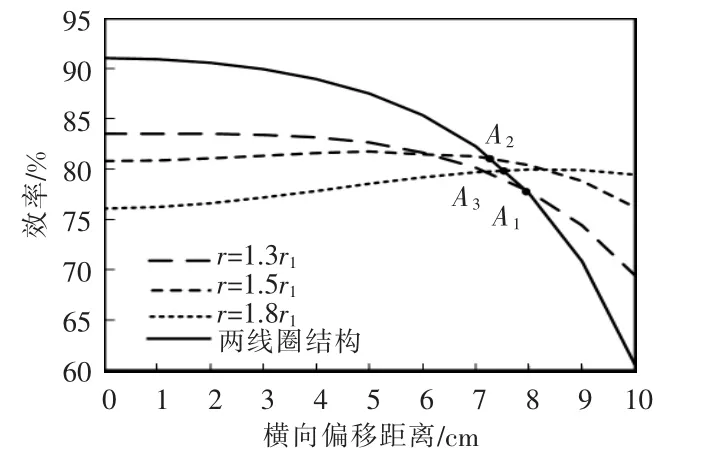
图9 两/三线圈结构效率随中继线圈尺寸变化的曲线Fig.9 Curves of efficiency of two-and three-coil structures with the size of relay coil

当发射与接收线圈尺寸固定的情况下，中继线圈尺寸可按以下步骤设计：首先，选择中继线圈匝数。为尽量减少中继线圈损耗，一般选择匝数为发射线圈匝数的一半。其次，确定中继线圈半径。改变中继线圈半径，可取r1到2r1范围内的任意值，绘出不同半径中继线圈的三线圈结构WPT 系统随横向偏移距离变化时的效率曲线，得到其与两线圈结构效率曲线的交点，即切换点。若仅考虑实际中小范围偏移为通常情况（即偏移距离不超过发射线圈半径），则选择偏移距离最小的切换点所对应的半径为中继线圈半径。

3 实验验证

根据图1 所示WPT 系统电路及图6 所示基于中继线圈切换的三线圈WPT 系统等效电路，搭建了实验平台。发射线圈、中继线圈及接收线圈均采用直径为1.5 mm 的利兹线，按照Maxwell 仿真尺寸绕制，线圈实物如图10 所示。该三线圈WPT 系统的电路参数如表1 所示。

当系统以两线圈结构工作时，系统实验波形如图11 所示。系统工作频率为82.101 kHz，输出功率为20 W。如图11（a）所示，当发射线圈与接收线圈无横向偏移时，逆变器输出电压us的有效值为19 V，发射线圈电流i1的有效值为1.27 A，输出直流电压uo为20.4 V，系统效率为91.7%。如图11（b）所示，发射线圈与接收线圈的横向偏移距离为5 cm 时，逆变器输出电压us的有效值为15 V，发射线圈电流i1的有效值为1.63 A，输出直流电压uo为19.9 V，系统效率为87.5%。如图11（c）所示，当发射线圈与接收线圈的横向偏移距离为10 cm 时，逆变器输出电压us的有效值为16 V，发射线圈电流i1的有效值为4.57 A，输出直流电压uo为20.8 V，系统效率为62%。可以看出，当偏移距离超过5 cm 时，系统以两线圈结构工作会表现较强的容性偏移，不利于逆变器的正常工作。

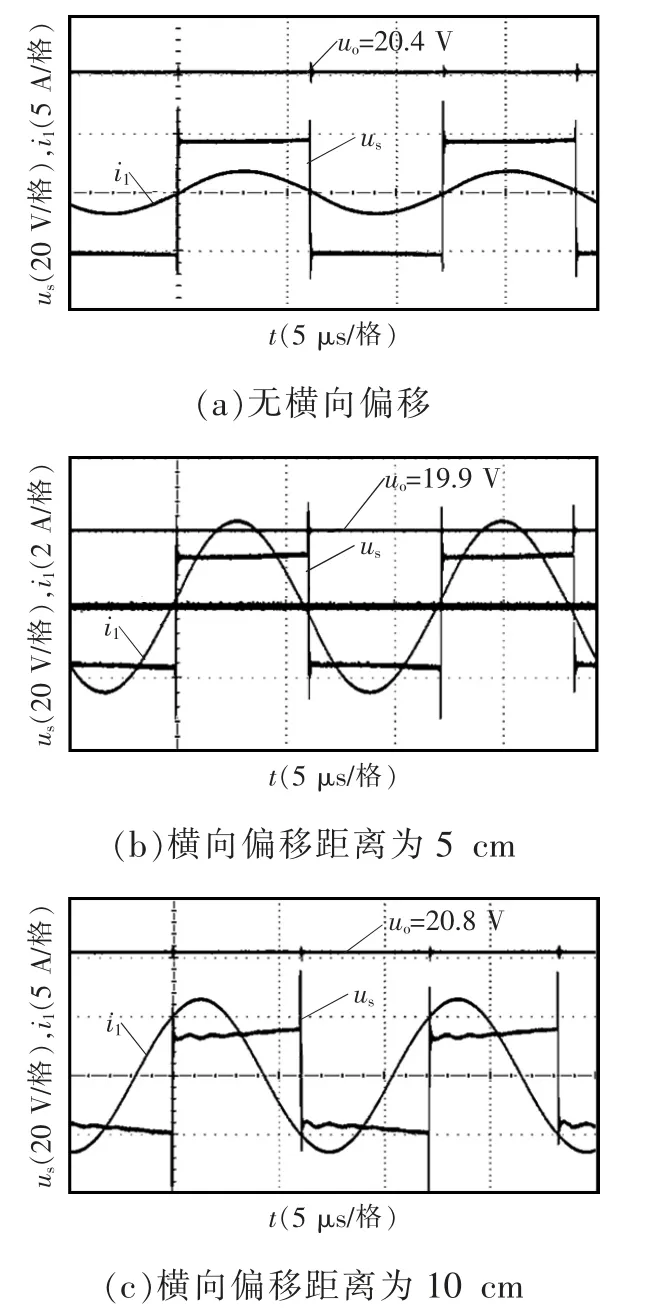
图11 两线圈结构WPT 系统的实验波形Fig.11 Experimental waveforms of two-coil WPT system

当系统以三线圈结构工作时，系统实验波形如图12 所示。系统工作频率为82.101 kHz，输出功率为20 W。如图12（a）所示，当发射线圈与接收线圈无横向偏移时，逆变器输出电压us的有效值为41 V，发射线圈电流i1的有效值为0.62 A，输出直流电压uo为20 V，系统效率为90.3%。如图12（b）所示，发射线圈与接收线圈的横向偏移距离为5 cm 时，逆变器输出电压us的有效值为39 V，发射线圈电流i1的有效值为0.65 A，输出直流电压uo为20.4 V，系统效率为89.9%。如图12（c）所示，当发射线圈与接收线圈的横向偏移距离为10 cm 时，逆变器输出电压us的有效值为43 V，发射线圈电流i1的有效值为0.68 A，输出直流电压uo为20.3 V，系统效率为85.9%。可以看出，在横向偏移距离为0～10 cm的范围内，系统以三线圈结构工作并不会出现容性偏移现象。

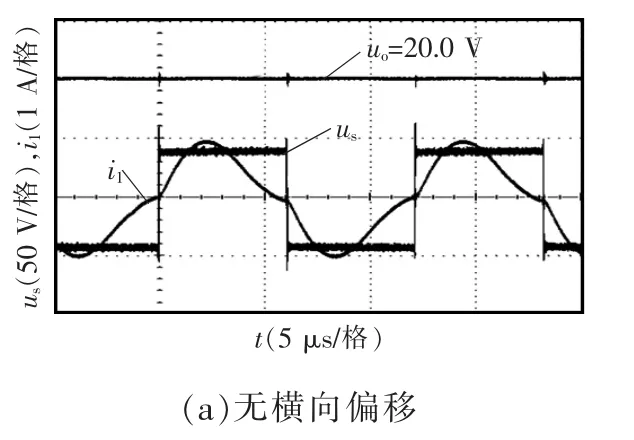
图12 三线圈结构WPT 系统的实验波形Fig.12 Experimental waveforms of three-coil WPT system

当系统输出功率为20 W 时，两线圈与三线圈结构的实验效率随横向偏移距离变化的曲线如图13 所示。可以看出，当横向偏移距离小于3 cm时，两线圈结构的效率高于三线圈结构。随着偏移距离由3 cm 增加至10 cm，两线圈结构的效率快速下降至62%，而三线圈结构的效率略微上升后缓慢下降至85.9%。因此，以A 点作为切换点，当横向偏移距离小于3 cm 时WPT 系统使用两线圈结构，当横向偏移距离大于3 cm 时WPT 系统使用三线圈结构，这样可以保证在横向偏移距离由0 cm 至10 cm 的变化过程中，系统效率始终保持在85%以上，且避免了容性偏移问题。

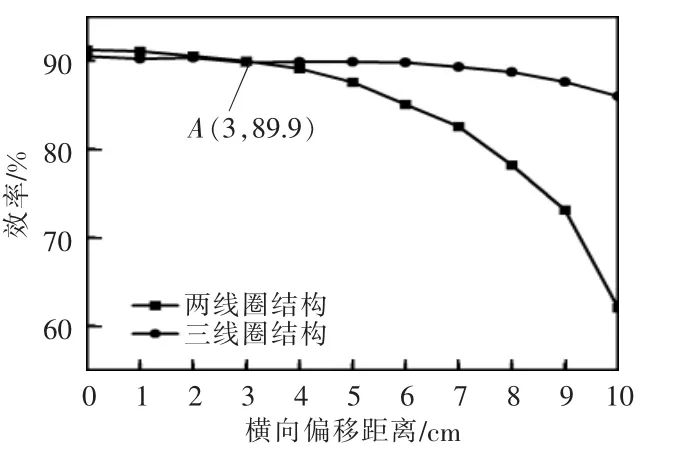
图13 两/三线圈结构WPT 系统实验效率随横向偏移距离变化的曲线Fig.13 Curves of experimental efficiency of two-and three-coil WPT systems against transverse misalignment

为证明本文所提方法的优势，将本文与已有文献中的系统进行比较，WPT 系统抗偏移性能对比如表2 所示，表中，τ 代表发射线圈尺寸。相较于文献[15]、文献[16]与文献[21]，本文所提方法避免了补偿网络设计，降低了系统设计的复杂度，且耦合机构更简单；文献[17]需要较大可移动空间，以保证系统在不同偏移状态下中继线圈能移动至最佳位置，而本文所提方法无需移动中继线圈位置，且中继线圈与发射线圈共面，空间利用率高。

表2 WPT 系统抗偏移性能对比Tab.2 Comparison of anti-misalignment capacity among several WPT systems

4 结语

本文建立了基于中继线圈的WPT 系统数学模型，分析了两线圈与三线圈结构WPT 系统效率随横向偏移距离的变化情况。结合两线圈结构在偏移距离近时效率高，而三线圈结构在偏移距离远时效率高的特点，提出了一种基于中继线圈切换的WPT 系统，并对其中继线圈半径进行了优化设计。最后，搭建了实验样机，结果表明，当横向偏移距离为10 cm 时系统效率下降仅5.1%，当在横向偏移距离在0～10 cm 范围内变化时，系统效率始终保持在85%以上。