近场源多频电磁法人工蜂群约束反演研究

2023-12-27周俊杰胡英才喻翔陈聪刘祜

世界核地质科学 2023年4期

周俊杰，胡英才，喻翔，陈聪，刘祜

（1.核工业北京地质研究院遥感信息与图像分析技术国家级重点实验室，北京 100029；2.核工业北京地质研究院中核集团铀资源勘查与评价技术重点实验室，北京 100029；3.中国核工业地质局，北京 100013）

近场源多频电磁法是一种人工源频率域电磁探测方法，通过发送和接收多个频率的电磁波来获取地下空间的电阻率分布信息［1］。该方法采用短收发距装置来采集近场源频率域电磁信号，具有采样密度高、施工速度快等特点，常被用于工程地质勘查、地下水勘探、环境评价及地下或水下隐伏目标探测等领域［2-6］。

与波区频率域电磁法不同，近源电磁场不能近似为平面波场，在计算电磁场分量时不可做简化。因此，近场源多频电磁法的高维正反演问题较为复杂，实际应用中仍以一维反演为主，常见的数据处理方法有视电导率转换法和电阻率反演法。相比于视电导率转换法，电阻率反演法不仅能获取平面异常，还能得到垂向电阻率分布信息［7-8］。目前，近场源多频电磁法数据反演的主流算法是最小二乘法［9-10］，其本质是将非线性问题线性化，通过多次迭代的方式来近似求解。然而，该方法在线性化逼近过程中会忽略高次项，在一定程度上造成精度损失，若计算参数或初始模型选取不当，反演可能会陷入局部极小而无法收敛［11］。因此，有必要引入非线性的反演方法来克服这些问题。人工蜂群算法是一种模拟自然界蜜蜂种群寻找蜜源的非线性群体智能算法，通过蜜蜂个体的局部寻优行为，最终在种群中搜索到全局最优值。该方法最早由Karaboga 提出，并迅速应用在地球物理相关问题上，如地震、大地电磁及重力勘探等［12］。相比于其他非线性方法，如模拟退火、遗传算法和神经网络等，该方法具有收敛速度快、稳定性好等优点，适用于求解近场源多频电磁反演问题［13-16］。

此外，过强的反演多解性还可能导致所得结果不符合实际情况。克服该问题最有效的办法就是在反演中引入先验信息约束。约束反演在重力、磁力、大地电磁和时频电磁等方法中的应用案例较多，但近场源多频电磁法的约束反演还有待研究［17-18］。在反演中引入先验信息约束有多种方式，如参考模型约束、物性范围约束和光滑模型约束等。综合使用各种类型的约束，可以从不同角度对反演问题的求解进行限制，从而更有效地改善反演结果质量，也更适用于实际勘探中的各种特定环境。

鉴于此，本文提出采用非线性的人工蜂群算法，同时引入参考模型、物性范围及光滑模型约束，实现近场源多频电磁法的人工蜂群约束反演。首先分析了近场源多频电磁法的正演问题，之后基于人工蜂群算法和多种约束条件构建了约束反演的目标函数，并设计相应的反演流程。理论模型测试和实测数据反演验证了该算法的可行性。

1 近场源多频电磁法正演问题

近场源多频电磁法通过偶极子源发射一次场，并在场源附近接收其二次场，从而获取地下导电介质的空间及电阻率等信息。通常用不接地的多匝线圈来模拟偶极子源，同时设置多匝线圈来接收电信号。该信号同时包含了一次场和二次场信息，但仅有二次场含有地下介质电阻率信息。二次场和一次场相比幅值极弱，因此在实际应用中，还要设置一补偿线圈，用来分离一次场和二次场。最终采用的观测参数为归一化二次场，即二次场Hs和一次场Hp之比［19］。

如图1 所示，在层状介质条件下，采用距离地面高度为h、收发距为ρ的水平共面装置进行探测，归一化二次场可写为［19］：

图1 层状大地模型下的近场源多频电磁法观测装置示意图Fig. 1 Observation configuration diagram of near source multi-frequency electromagnetic method based on layered earth model

式（1）中：积分项可采用汉克尔变换的数值滤波算法求解［20］，积分核中的rTE为反射系数，可由公式计算：

公式（1）中的u0及公式（2）式中的Y和Ŷ与层电阻率、层厚度、层磁导率及圆频率等参数相关，可按照Huang［21］给出的解析求解公式计算得到。

正演计算是反演求解的基础。为验证正演计算可靠性，采用Huang［1］所述的三层理论模型进行验证，层电阻率由上至下依次为100、5 和200 Ω·m，层厚度依次为15、5 m。当发射频率为2 000 Hz 时，同向分量和正交分量的误差分别为2.82 %和0.47 %，如表1 所示，达到了反演的精度要求。尽管同向分量和正交分量都蕴含有地下介质的电阻率信息，但在实测数据中正交分量的信噪比更高，因此在实际应用中反演算法通常仅采用正交分量［9］。

表1 三层理论模型的正演响应数据验证Table 1 Forward response data validation of three-layer synthetic model

2 近场源多频电磁法反演问题

2.1 人工蜂群算法

受蜜蜂种群有组织规律的寻蜜活动启发，Karaboga 提出了模拟蜜蜂种群寻蜜行为的人工蜂群算法，用以解决多参数、多维度非线性最优化问题［12］。该算法涉及到蜜源、蜜蜂两个概念。算法首先随机生成若干个已知蜜源，并派出蜜蜂前往寻蜜。蜜蜂种群中的个体可分为三类，分别为引领蜂、跟随蜂和侦查蜂。引领蜂负责搜索已知蜜源邻域内更好的蜜源，并向跟随蜂分享信息；跟随蜂对引领蜂所分享的蜜源进行轮盘赌式随机选择，且更倾向于选择优质的蜜源，之后在蜜源邻域内搜索更好的蜜源；当在某个蜜源邻域内长期搜索不到更好的蜜源时，侦查蜂放弃该蜜源，并随机搜索新的蜜源。随着蜜蜂种群的轮番寻蜜，蜜源将不断被更新迭代，其质量也将逐步提高，直到搜索到最优蜜源为止。

在人工蜂群算法中，蜜源对应非线性问题的某个可能解。蜜源的质量好坏由其对应的目标函数值来衡量。目标函数值越小，蜜源质量越高，更有可能成为最终解。三类蜜蜂个体则对这些解的质量进行判定并选择质优者。虽然单个蜜蜂的行为是随机的，但蜜蜂种群的整体行为是确定的。从最优化问题角度看，三类蜜蜂在寻优过程中分工协作，从而使人工蜂群算法具备全局寻优且能快速收敛的能力。其中，引领蜂的作用是通过邻域随机搜索来维持当前的最优解；跟随蜂的作用是依托最优解继续寻优，有助于提高收敛速度；侦查蜂的作用是跳出当前的局部极小值，从而获得了全局非线性搜索能力。

对于近场源多频电磁法反演问题，蜜源相当于电阻率模型向量，其质量值fi的计算公式为：

式（4）中：φi—第i个蜜源的数据拟合目标函数，即观测数据向量dobs和正演响应f（mi）之差的二范数。蜜蜂种群对一系列蜜源向量进行搜索，相当于对多组电阻率模型的正演响应与观测参数进行同步比对，获取最优电阻率模型。蜜蜂通过在蜜源领域搜索找到新的蜜源向量，相当于对当前电阻率模型进行扰动，产生新的电阻率模型。蜜蜂种群按照引领蜂、跟随蜂和侦查蜂的顺序不断搜索迭代，相当于电阻率模型被不断比对、更新，其与观测参数差异越来越小，正演响应逐步与观测参数达到拟合，从而找到最终的电阻率向量解。

基于上述思路，可构建近场源多频电磁法的人工蜂群反演算法，如图2 所示。在确定蜜源向量的数目及蜜蜂的种群规模后，随机生成初始蜜源向量群并衡量其质量值，找到当前最优蜜源向量。若没有达到给定阈值，则依次派出引领蜂、跟随蜂和侦查蜂寻蜜。引领蜂随机选取某个当前蜜源向量并在其邻域搜索，产生1个新的蜜源向量，其元素的表达式为：

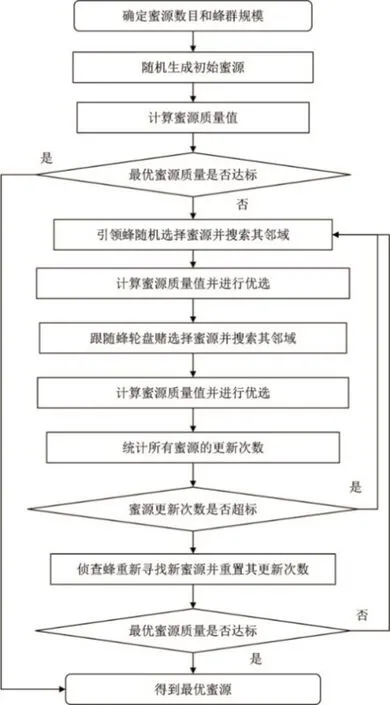
图2 人工蜂群反演算法流程图Fig. 2 Flow chart of artificial bee colony inversion algorithm

式（5）中：xij—更新前的第i个蜜源向量中的第j个元素；vij—更新后的相应元素。利用该公式可实现蜜源向量的邻域扰动。随后，引领蜂对比前后两个蜜源向量的质量，若优于前者，则用新蜜源替换旧蜜源；反之，则保留旧蜜源，并记录当前蜜源的总尝试次数。通过引领蜂的寻蜜，反演将得到一组更新后质量相对更优的蜜源向量组。

引领蜂寻蜜完成后，跟随蜂将对更新后的蜜源的质量进行分析，并以轮盘赌的方式随机选择蜜源，选择概率pi的表达式为：

式（6）中：fi—第i个蜜源的质量值，可通过数据拟合目标函数计算得到。可见，蜜源质量越高，被搜寻的概率越大。选择蜜源后，跟随蜂也将在蜜源邻域进行搜索，其搜索过程与引领蜂相同。跟随蜂搜索完毕后，反演将继续得到一组新的质量更优的蜜源向量组。

跟随蜂寻蜜完成后，考察所有蜜源的尝试次数，若超出给定阈值，则派出侦查蜂。侦查蜂放弃已知的蜜源信息，重新寻找新的蜜源，并重置该蜜源的尝试次数为0。侦查蜂搜索完毕后，反演将继续得到一组新蜜源向量组，且其中引入了崭新的蜜源。该蜜源的质量未必优于其他蜜源，但在随后迭代中，引领蜂和跟随蜂将在其附近进行寻蜜，从而保证了最终蜜源为全局最优解。

2.2 约束的引入

人工蜂群算法用完全非线性的方式解决了反演可能陷入局部极小的问题，但要获取可靠的反演解，还需要引入先验信息约束。在实际反演中，常见的先验信息有工区典型物性值、物性参考范围等，这些信息均可在反演中发挥作用。此外，还可假设反演的层状模型具有光滑特性。引入光滑假设会使模型损失尖锐边界信息，但却能有效克服虚假冗余异常所带来的干扰，因此对降低反演多解性是非常必要的。

公式（4）给出了观测数据拟合的目标函数项，在此基础上可继续追加光滑约束项和参考模型约束项，将公式（4）扩展为：

式（7）中：α和β分别为光滑约束项和参考模型约束项的权重因子；D—差分矩阵；mref—参考模型向量。根据公式（7）计算得到的人工蜂群蜜源质量值将综合反映数据拟合项、模型光滑项和参考模型约束项，各项权重可通过权重因子调节。对于物性范围信息，人工蜂群反演在产生蜜源时可直接将其引入来做限制，此时蜜源的第i个元素mi表达式为：

式（8）中：mmin和mmax分别为下边界和上边界。在更新蜜源时，引入硬约束来进行限制，可令超出物性范围的值强行等于边界值。在施加参考模型约束、模型光滑度约束和物性范围约束后，人工蜂群反演过程将受约束限制。在多种先验信息的共同作用下，获得光滑度更高、物性值符合预设要求且倾向于具备参考模型基本特征的最终结果。

相较于常规的最小二乘反演，人工蜂群反演在施加约束时具有天然的优势。在引入参考模型项和模型光滑度项时，最小二乘反演需要对待求解的反演方程进行整体改造，而人工蜂群反演无需对算法做出大幅调整，仅需在计算蜜源质量值时修改目标函数公式即可。最小二乘法引入物性范围约束需要采用变量代换法、对数障碍法等，增高了算法复杂度；若直接施加硬约束，则可能改变反演搜索方向，影响反演迭代收敛的稳定性。人工蜂群算法的随机搜索特性使其无需借助其他算法也可直接引入物性范围信息，即使采用硬约束也不会造成反演迭代的不稳定。

3 理论算例分析

为了验证近场源多频电磁法人工蜂群约束反演的有效性，选择典型层状理论模型作为研究目标，将其正演响应附加5 %的随机噪声作为观测数据进行反演。首先对反演参数的设置进行分析，之后对比先验信息的引入对反演结果的影响，最后将人工蜂群约束反演与常规最小二乘反演做比较，用多层复杂模型来阐述其优势所在。

3.1 反演参数设置

在反演之前，人工蜂群约束反演算法需要先设置模型层数、蜜源数目及蜂群规模、尝试次数、权重系数。

模型层对反演的垂向分辨率有直接影响，较多的层数能使反演具有较强的分辨能力，但随着层数增多，垂向分辨能力将趋于饱和。通常可将反演层厚设置为最薄地层厚度的0.5～1 倍，即可达到较为理想的效果。人工蜂群算法的蜜源数目和蜂群规模与反演收敛速度相关。侯征等［11］对此设定进行了研究，提出应在反演收敛与计算时间耗费间做平衡，通常可选择蜜源数目为层数的1～2 倍，且蜂群规模与蜜源数目保持一致。尝试次数对算法跳出局部极小具有重要意义，过少的尝试次数会使反演频繁放弃质量较高的解，从而延缓收敛速度。侯征等［11］通过实验分析认为，尝试次数约为最大迭代次数的2/3时效果较好。权重系数用于调节数据拟合与模型拟合之间的平衡，一般应在保证数据拟合的前提下，尽可能提高模型拟合程度，可通过多次试验的方法来确定合适的权重因子［22］。

图3 和4 为不同层数条件下，三层理论模型的反演拟合曲线和结果模型。在数据拟合相当的情况下，3 层反演结果与理论模型匹配度最高，6 层和12 层反演结果均出现较大偏离。尤其是12 层模型，在深处出现了的电阻率值震荡较多，造成虚假异常。然而在实际应用中，地层的复杂性往往要求层数设置不能太少。未引入约束的人工蜂群反演不能满足多层反演的需求。

图3 不同层数的人工蜂群反演正交分量拟合曲线图Fig. 3 The fitting curves of quadrature component of artificial bee colony inversion with different number of layers

图5 展示了不同的种群规模和尝试次数设置下人工蜂群反演的迭代收敛情况，使用的理论模型数据与图4 相同。三种方式下蜜源数目和尝试次数参数设置分别为：20 和100；10 和100；20 和50。可见，人工蜂群反演的迭代都是稳定收敛的，且达到局部极小值后会有在一定区间内保持不变而显示为直线，直到进一步找到更优的极小点。当蜜源数目较多和尝试次数较少时，反演的收敛速度较快，如图5 中红色曲线，在20次以内即达到全局极小。在实际应用中，应充分考虑计算效率和反演收敛性。若收敛过慢，应增大蜜源数目；若反演易陷入局部极小而无法达到数据拟合时，则应增大尝试次数；当计算耗时过长时，可适当减小蜜源数目和尝试次数。

图4 不同层数的人工蜂群反演结果Fig. 4 The results of artificial bee colony inversion with different number of layers

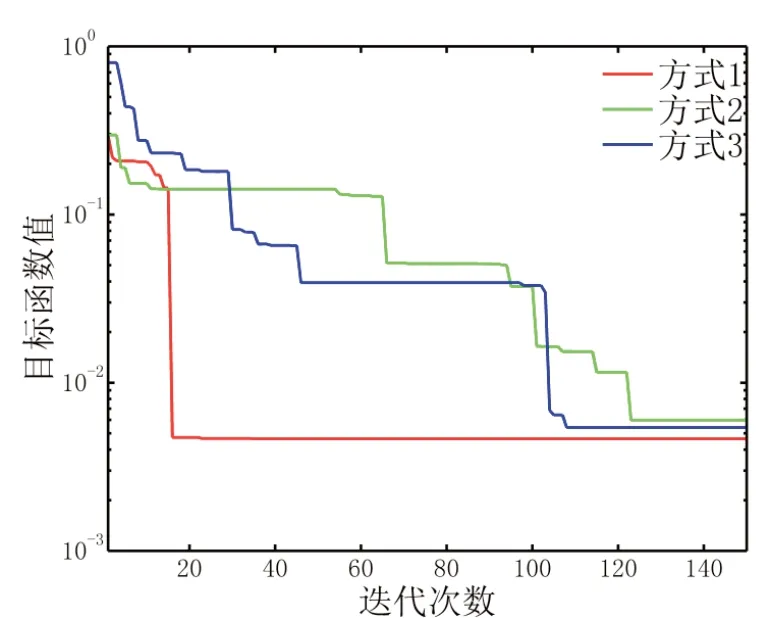
图5 不同参数设置下人工蜂群反演迭代收敛曲线图Fig. 5 Convergence curve of artificial colony inversion iteration with different parameter settings

3.2 约束信息的影响

以图4 所示理论模型为基础，考察物性范围、参考模型及光滑约束的引入对反演的影响。设置层数为12，给定物性范围为0.1和1 000 Ω·m，反演所得结果如图6 所示。与图4 对比，反演得到的层电阻率更接近真实值，且都处于给定范围之内。因此，物性范围可对反演结果起到改善作用，但低阻异常位置与真实情况并不相符。继续添加约束信息，修改光滑约束权重因子为0.001，所得反演结果如图7 所示。此时反演结果的光滑度得到提高，低阻体的深度对应更好，但深部的高阻层没有体现。最后再追加参考模型信息，假定当地典型电阻率值为100 Ω·m，将其作为已知信息代入反演中，赋予相应的权重因子0.001，结果如图8 所示。可见，随着约束信息的不断引入，反演结果的质量得到逐步提高，最终获得的结果与理论模型吻合很好，同时具有较好的光滑特性，且不存在虚假异常。

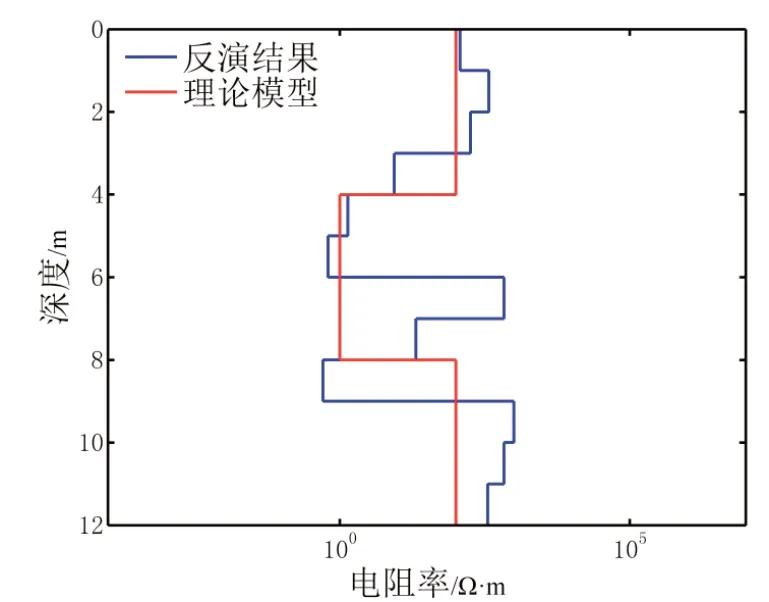
图6 引入物性范围信息的人工蜂群约束反演结果Fig. 6 Inversion results of artificial bee colonies with physical property bound constraints

图7 引入物性范围和光滑度的人工蜂群约束反演结果Fig. 7 Inversion results of artificial bee colonies with physical property bound and smooth constraints

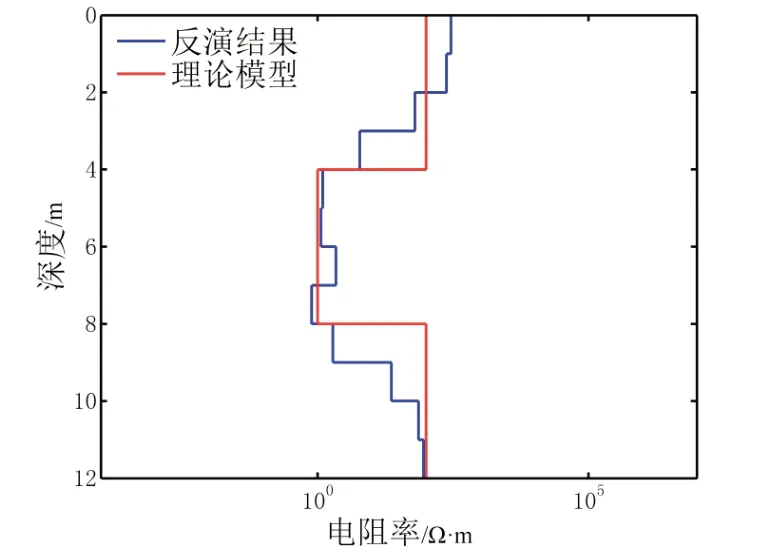
图8 引入物性范围、光滑度和参考模型信息的人工蜂群约束反演结果Fig. 8 Results of artificial colony inversion with physical property bound，smoothing and reference model constraints

3.3 与常规反演的效果对比

选择更为复杂的多层模型理论数据对人工蜂群约束反演算法和常规最小二乘算法进行对比，使用的反演参数均相同，所得反演结果分别如图9和10所示。与理论模型相比，两种反演结果对高阻和低阻均有呈现，尽管深度位置不完全匹配，但特征是吻合的；人工蜂群算法的反演结果物性范围更接近真实情况，且模型光滑度更好。总体而言，人工蜂群算法的结果要优于最小二乘算法。图11 为两种反演结果的迭代收敛曲线，两者表现有很大的不同。人工蜂群算法的收敛曲线是稳定下降的，体现了收敛的稳定性，而最小二乘算法的收敛曲线跳动很大。在迭代过程中，最小二乘反演也可获取较小的目标函数值，但其并不能保证搜索方向的正确性，反而使后续的曲线拟合变得更差。此外，从最终的电阻率结果也可以看出，最小二乘算法有部分层位的电阻率处在物性边界上，说明此时模型更新是失效的；而人工蜂群算法所有层位均在物性范围内，没有出现畸形层位。

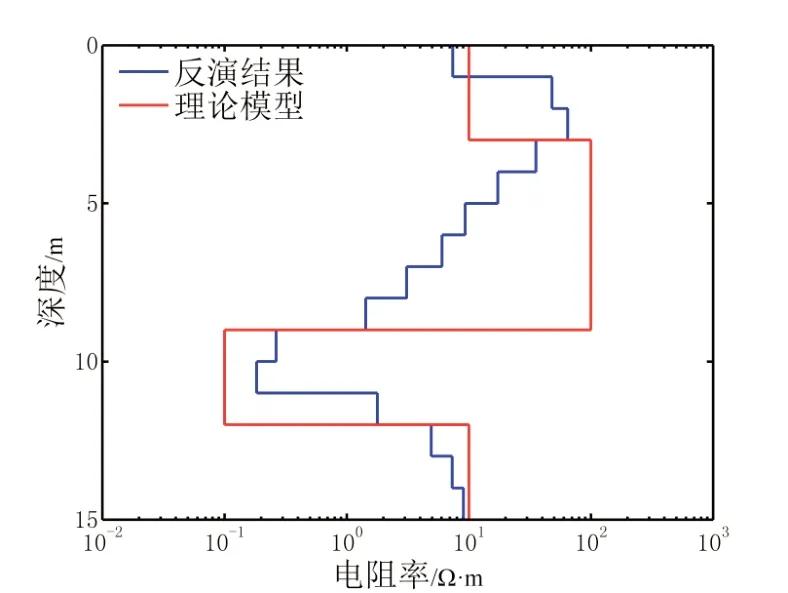
图9 多层复杂理论模型的人工蜂群约束反演结果Fig. 9 Results of artificial bee colony constrained inversion of multilayer complex synthetic model

图10 多层复杂理论模型的最小二乘约束反演结果Fig. 10 Results of least square constrained inversion of multilayer complex synthetic model

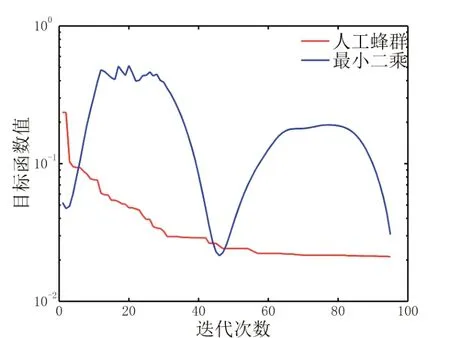
图11 人工蜂群约束反演和最小二乘约束反演迭代收敛曲线Fig. 11 Iterative convergence curve of artificial bee colony constrained inversion and least square constrained inversion

4 实测案例分析

4.1 案例1：垃圾填埋范围探测

生活及建筑垃圾填埋不当可能会造成地下渗漏污染。对垃圾填埋及渗漏范围进行探查，有助于开展有针对性的环境治理。使用近场源多频电磁法对在山东烟台某处垃圾填埋地进行局部探测，获取了频率域电磁测线数据1 条。对数据点进行均匀插值、系统误差校正及随机干扰校正等处理后［23］，使用人工蜂群约束反演算法计算得到地下电阻率分布图，如图13 所示，相应的观测数据及拟合曲线如图12 所示。测量区域为第四系松散覆盖物，故设定较为宽松的电阻率范围0.01～1 000 Ω·m，参考电阻率模型为100 Ω·m 的均匀半空间，经多次测试，权重因子设为0.01 即能在满足数据拟合要求的前提下，也能获得较光滑且与参考模型相近的结果。可见，人工蜂群约束反演得到的电阻率剖面能较好地反映地下5 m 以内电性结构。剖面显示，在剖面距22～25 m的范围内地表1～3 m（区域C）显示为低阻，剖面距7～10 m 范围及13～19 m 范围区域内深部3～5 m（区域A 和区域B）显示为低阻。推测区域C 为地表垃圾掩埋点，区域A 和区域B 为垃圾覆盖点或渗漏点，且两者在深部可能具有一定连通性。实际开挖结果显示：在圈定的3个区域内均有垃圾填埋物，且所处深度与推断结果相吻合。此实测案例表明：近场源人工蜂群约束反演在解决浅地表低阻区探测方面具有成效。

图13 人工蜂群约束反演结果与低阻区解译Fig. 13 Artificial bee colony constrained inversion results and interpretation of low resistence zones

4.2 案例2：海域水下金属目标探测

海水的电阻率约为3 Ω·m，但和低阻金属目标电阻率相比仍是相对高阻，因此在海域探测金属目标具有可行性［24］。在山东渤海近海域开展水下金属目标探测实验，将近场源多频电磁仪搭载在水面无磁支架上，获取了频率域电磁测线数据1 条。采用第4.1 节所述处理方法，对观测数据进行插值及各项校正后，使用人工蜂群约束反演算法计算得到水下电阻率分布图，如图15 所示，相应的观测数据及拟合曲线如图14 所示。可见，正交分量对金属目标的敏感度很高，形成明显异常，但仅凭观测数据难以判断金属目标埋深及规模等信息。

图14 近场源多频电磁案例两观测曲线与反演拟合曲线Fig. 14 Near source multi-frequency electromagnetic observation curve and inversion fitting curve of case 2

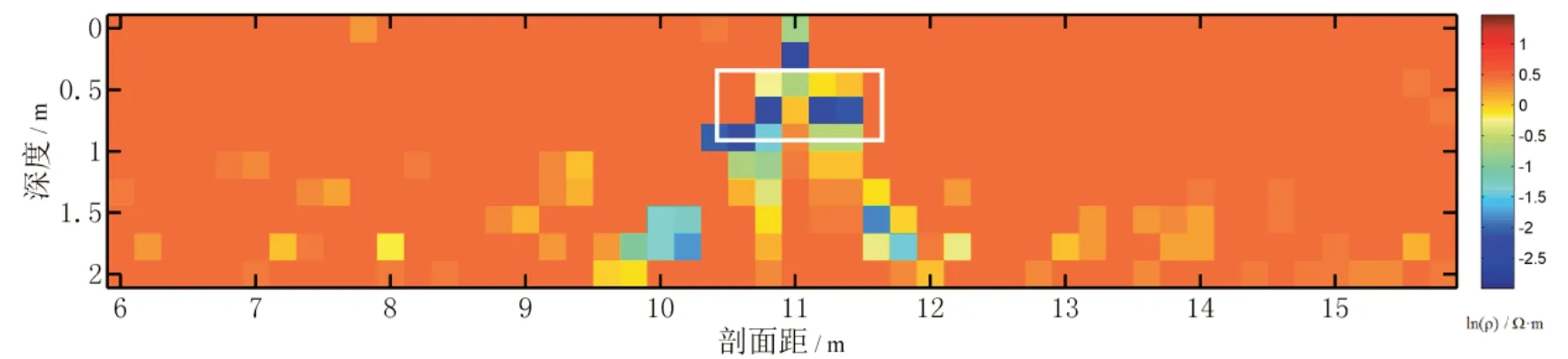
图15 人工蜂群约束反演结果与海域金属目标解译Fig. 15 Artificial bee colony constrained inversion results and interpretation of metal targets in sea area

海水介质的电阻率均一性很高，因此在反演中可给定介于0.001～3 Ω·m 之间的较窄的电阻率范围，参考电阻率模型可选为均匀半空间，电阻率为3 Ω·m。经多次测试，将权重因子设为0.000 1，以满足反演的数据拟合及模型拟合的需要。相较于案例1，本例电阻率反演结果的浅部更为平滑，且数值大多与海水电阻率3 Ω·m 极为接近。先验信息的引入起到明显作用，使得反演解范围收紧，从而使反演结果更靠近真实情况。深部出现少量电阻率幅值的震荡现象，这是由于深度敏感度降低造成的。在异常位置处，反演出明显的低阻异常，其宽约1 m，中心深度约0.5 m，与预先放置的金属目标的实际宽度与深度相符。