基于改进自适应高阶滑模的液压缸位移跟踪控制

路时雨，鄂东辰，董兴华，刘超强，蔡玉强，董小雷

(1.华北理工大学机械工程学院，河北唐山 063210；2.唐山工业职业技术学院，河北唐山 063299)

0 前言

阀控缸电液伺服系统具有功率密度大、响应速度快等优点，被广泛应用于工程机械、武器装备和航空航天等领域。液压缸的运动精度决定了主机的动态性能，例如：液压驱动抓取机械手要求液压缸具有高的定位精度，便于顺利抓到重物；车辆的道路模拟平台要求液压缸具有高的位移跟踪精度，以保证路况的真实再现。但是，由于主机执行机构中零件的间隙、油液的可压缩性和变负载等一些不确定因素的影响，使得基于模型的控制方法不能达到人们所希望的运动性能。对此研究人员提出了多种鲁棒控制方法以消除未建模不确定因素的影响，例如滑模控制[1]、反步法[2]和模型自适应控制[3]等。其中滑模控制具有算法简单、鲁棒性好等优点，受到广泛关注。该方法通过构造包含状态变量的滑模面函数，根据Lyapunov稳定性理论设计控制器保证滑模面函数渐近稳定，使得状态变量趋近于零。当把滑模面函数中的状态变量替换为状态的真实与期望值之差时，状态归零控制问题转变为状态跟踪控制问题。通过设计滑模面函数可以调节状态变量到滑模面的趋近速度。当状态变量到达滑模面后，系统将保持在滑模面上运动，并对不确定因素不敏感，体现了控制算法的鲁棒性。抖动问题是制约滑模控制应用的主要障碍。在理想情况下，状态变量会沿着滑模面趋近于零。但实际中存在控制器延时和执行机构的惯性，都会导致状态变量不能始终保持在滑模面上，控制器始终处在调节状态，表现为液压缸活塞在位移跟踪的同时伴随着小幅抖动。

针对滑模控制的抖动问题，研究人员提出许多可行的方案，例如，用连续函数代替sgn函数[4-5]，动态边界层滑模控制[6-7]，以及高阶滑模控制[8-9]等。其中高阶滑模控制将不连续的sgn函数包含在控制信号的导数当中，再通过积分运算消除了控制器的不连续，从而抑制抖动。针对高阶滑模控制，前人已做了大量的研究。李运华等[10]将时间最优与二阶滑模控制相结合，以抑制系统抖动的同时提高系统的响应速度。任彦等人[11]将高阶终端滑模控制算法应用于光电稳定平台的控制当中。姚崇等人[12]提出自适应高阶滑模算法，对船用发动机电子节气门进行控制。杜文正等[13]将高阶滑模控制应用于液压起竖装备当中。宋胜利等[14]提出一种收敛速度快的二阶终端滑模控制算法，并将该算法应用于下肢骨骼的姿态控制。殷凯轩等[15]将滑模扰动观测器与分数阶积分补偿相结合，以提高永磁同步电机转速控制的鲁棒性。

本文作者针对高阶滑模控制器参数设定缺乏理论依据的问题，提出根据时滞控制(Time Delay Control，TDC)算法[16-17]实时估计系统的总扰动，再将估计值作为控制器的参数，使控制器可以根据总扰动自适应调节，既保证了系统渐近稳定又进一步降低了控制信号的抖动幅度。由于高阶滑模本身的特点，需要对控制器的导数进行积分运算，积分环节的引入会使系统的响应速度降低，增大了跟踪误差。对此提出将自适应高阶滑模控制与比例控制相结合的控制策略，通过自适应高阶滑模解决模型不确定问题，通过比例控制解决响应速度慢的问题。最后通过液压系统的仿真分析验证该控制策略的性能。

1 液压系统数学模型

伺服阀控制液压缸系统如图1所示。液压泵为系统提供油液。溢流阀用来稳定系统压力。伺服阀通过阀芯的高频运动，改变进入液压缸的流量，实现对活塞位移的控制。其数学模型包括：油液的流量连续性方程、液压缸活塞的受力平衡方程以及伺服阀控制电压与阀芯位移的关系方程。

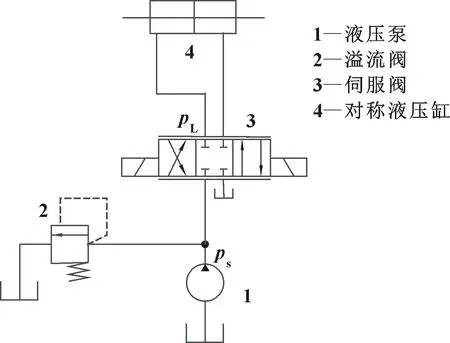
图1 阀控缸电液位置伺服系统

根据薄壁小孔的流量公式得伺服阀的的流量方程为

(1)

其中：QL为流经伺服阀的流量；Cd为伺服阀口的流量系数；w为伺服阀口的面积梯度；xv为阀芯位移；ps为伺服阀入口压力；pL为伺服阀出口压力；ρ为液压油密度。

液压缸的流量连续性方程为

(2)

式中：Ap为液压缸活塞的油液作用面积；Ct为液压缸的内泄漏系数；V为液压缸进油腔的容积；βe为油液的体积弹性模量。

液压缸活塞的受力平衡方程为

(3)

式中：mt为活塞质量；Bp为活塞与缸筒内壁之间摩擦力的黏性阻尼系数；k为负载弹簧刚度；FL为外负载。液压缸在工作过程中其负载通常是变换的，因此文中将FL设定为不确定因素。

伺服放大器等效为比例环节。伺服阀的输入电流与阀芯位移之间的关系也近似为比例环节，则有：

kp=i/u

(4)

ksv=xv/i

(5)

式中：kp为伺服放大器的放大系数；ksv为xv与输入电流i的比例系数；u为控制电压。

根据式(1)—(5)整理出系统的状态方程和输出方程分别为式(6)和式(7)。其中3个状态变量x1、x2、x3分别代表液压缸活塞的位移、速度和加速度。

(6)

y=x1

(7)

2 高阶滑模控制

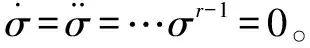
针对前文电液伺服系统的状态方程，设计滑模面函数为

σ=c1e1+c2e2+e3

(8)

其中：e1=x1-x1d，e2=x2-x2d，e3=x3-x3d，x1d、x2d、x3d分别为x1、x2、x3的期望运动轨迹；c1、c2为设计参数。对式(8)求二阶导数，并将式(6)代入得

(9)

设计二阶滑模趋近率为

(10)

(11)

式中：等号右边的u为前一采样时刻的控制信号。

通过Lyapunov稳定性理论证明控制器[式(11)]使系统渐近稳定。设由σ构造正定的Lyapunov函数为

(12)

对式(12)求导得：

(13)

将式(9)(11)代入式(13)得：

(14)

3 自适应高阶滑模控制

TDC假设当采样间隔很短时，前一采样时刻的u可以近似代替当前时刻的u。根据该假设由公式(9)推导出当前时刻总扰动估计的计算公式为

(15)

(16)

将式(9)(16)代入式(13)得：

(17)

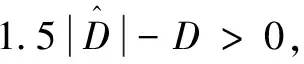
4 高阶滑模与比例的复合控制策略

(18)

其中：u为自适应高阶滑模控制信号；k1为比例系数。控制算法的构建思路如图2所示。

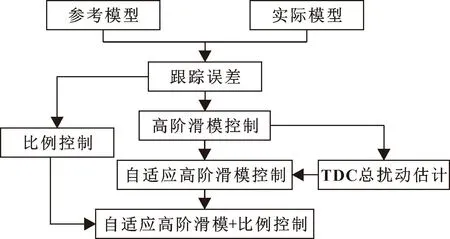
图2 控制算法的构建思路

5 仿真分析

通过建立伺服阀控制液压缸的Simulink仿真模型，对比分析所提出的控制策略的性能。仿真模型主要包括参考模型和实际模型两部分，其中参考模型为伺服阀控制液压缸的理想状态方程，其参数均已知且固定。当参考模型中加入不确定因素后即为实际模型。控制目标为：在有不确定因素条件下实际模型的状态变量能够跟随参考模型的状态变量，跟随误差越小控制效果越好。设定参考模型的控制信号为

(19)

仿真模型的参数如表1所示。

表1 仿真模型参数

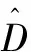
图3 负载曲线

控制器的参数如表2所示。

表2 控制器参数

5.1 控制信号抖动分析

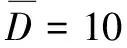
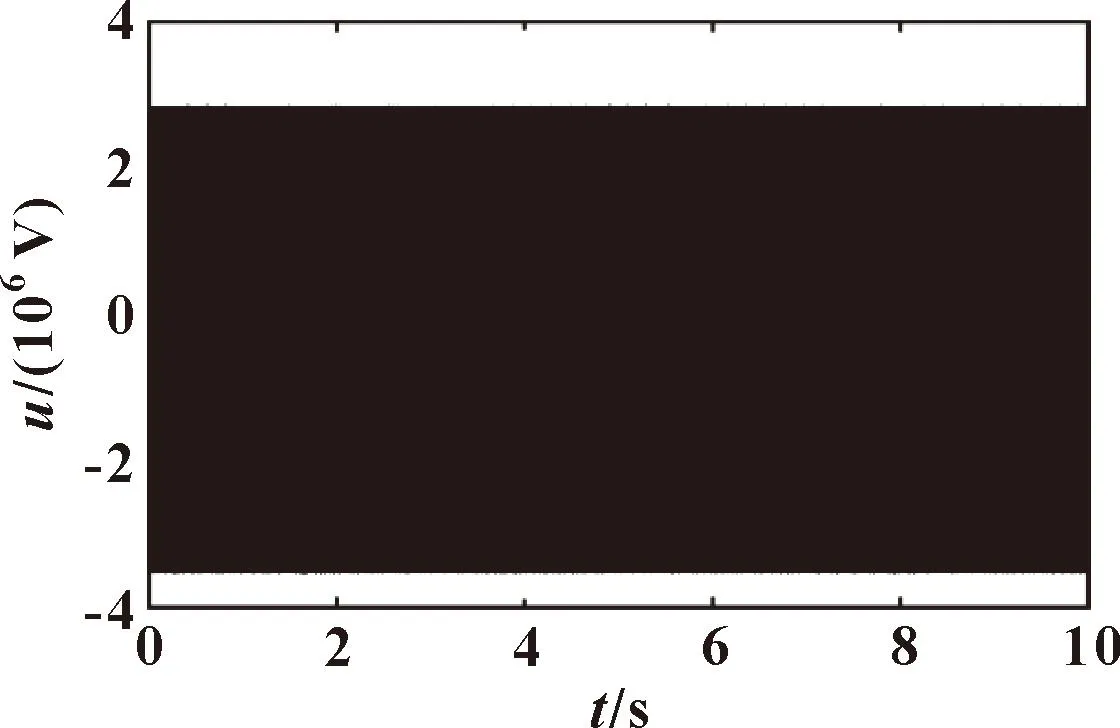
图5 自适应一阶滑模控制信号

图6 高阶滑模控制信号

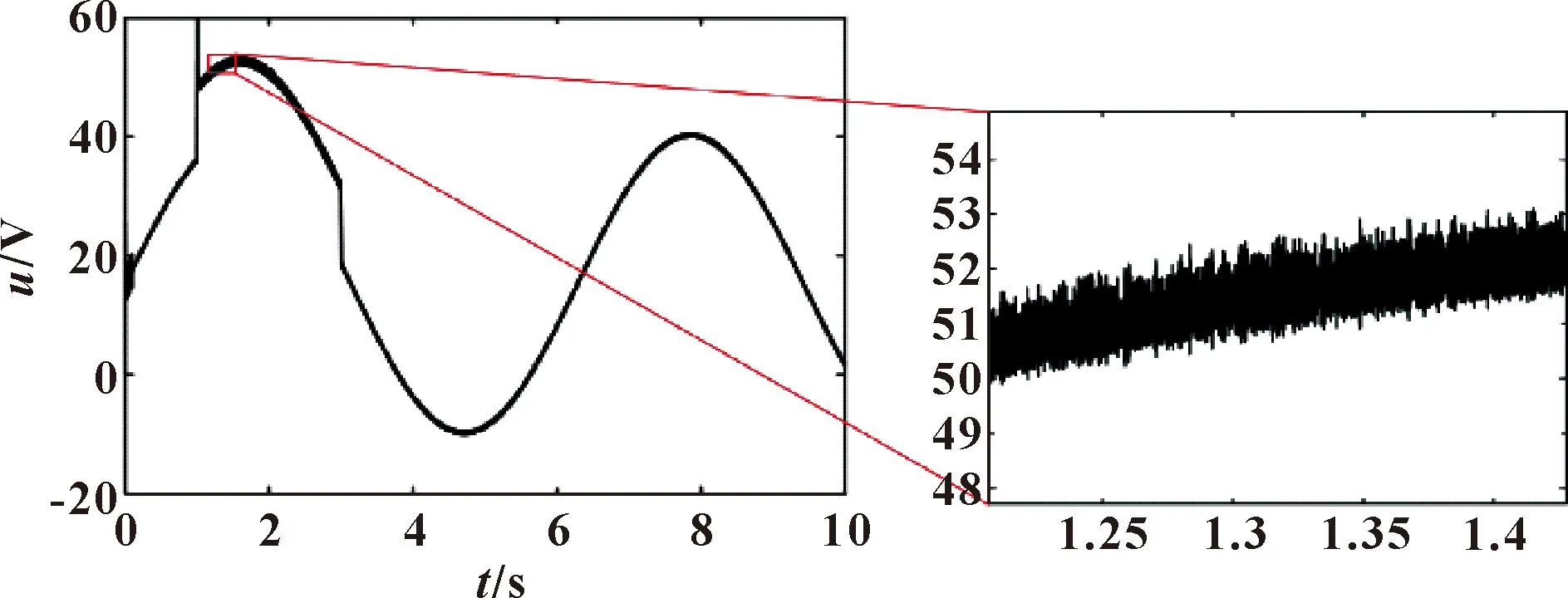
图7 自适应高阶滑模控制信号

5.2 跟踪误差分析

分别采用自适应高阶滑模和自适应高阶滑模+比例的复合控制策略仿真得出x1如图8、9所示。在自适应高阶滑模控制下的最大e1=9.1×10-12m，在复合控制下的最大e1=1.8×10-12m。位移跟踪误差如图10所示。可见复合控制使e1迅速减小，并稳定在小幅值范围内。自适应高阶滑模控制的e1幅值较大，需要较长的时间使e1调整到小误差范围内，说明了复合控制策略的优越性。

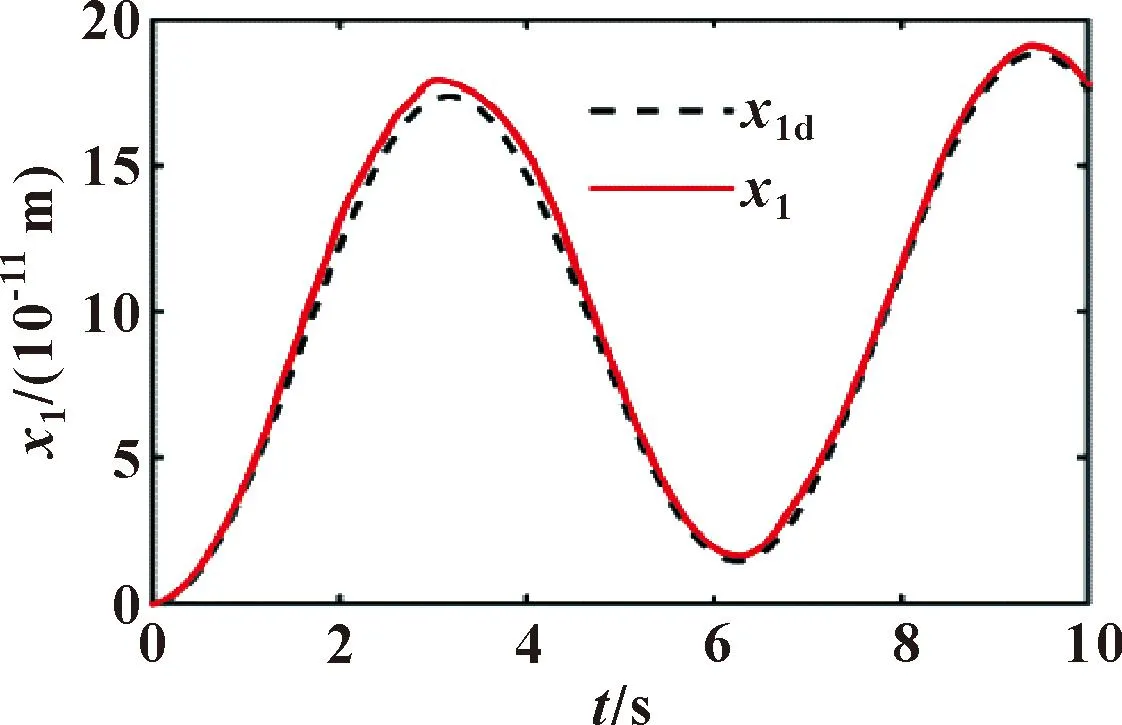
图8 高阶滑模控制下的液压缸位移

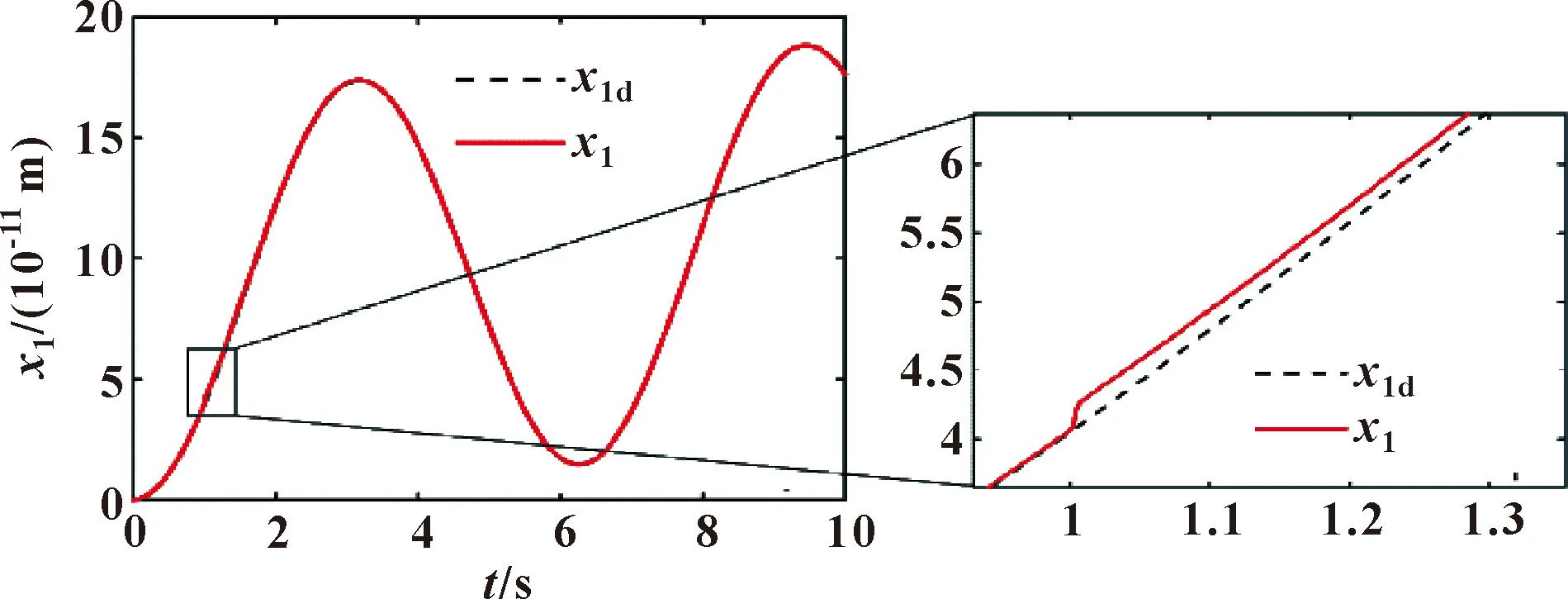
图9 复合控制下的液压缸位移

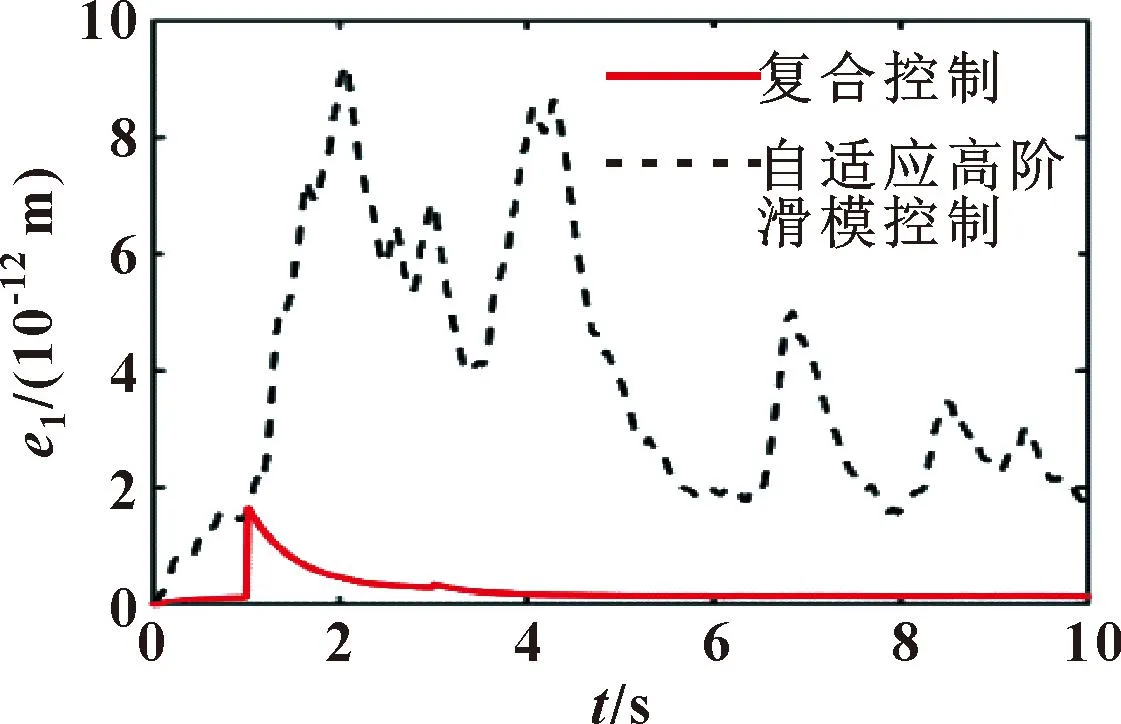
图10 液压缸位移跟踪误差

6 结论

(1)针对高阶滑模控制器中总扰动的上限无法预知的问题，提出通过TDC算法实时估计系统的总扰动，并根据估计值自适应调整控制器的参数，既保证了系统渐近稳定又进一步降低了控制信号的抖动幅值。伺服阀控制液压缸的仿真结果表明：自适应高阶滑模控制信号的抖动幅值相对一阶滑模的抖动幅值减小了约4×106倍，相对高阶滑模减小了约60倍。为抑制滑模控制算法引起的系统抖动提供了解决方案。

(2)针对高阶滑模控制算法使系统的响应速度慢的问题，提出在自适应高阶滑模控制的基础上加入比例控制以提高系统的响应速度。仿真结果表明：加入比例控制后的液压缸位移响应速度大幅提高，跟踪误差也显著减小，验证了文中提出的控制策略的优越性。