基于轨迹压缩的机器人轨迹插值与仿真
2023-12-20张培森郭忠峰杜文龙彭世杰
张培森,郭忠峰,杜文龙,彭世杰
(1.沈阳工业大学机械工程学院,辽宁沈阳 110870;2.中船九江海洋装备(集团)有限公司,江西九江 332000)
0 前言
机器人技术的创新与发展对工业自动化具有重大实际意义,被广泛应用于搬运、装配、焊接、喷漆等行业,降低人工成本,提高工作效率。机器人的研究是设计开发应用的基础,机器人轨迹规划领域的研究则是解决问题的前提和基础[1-2]。为了实现机器人平稳、高效地完成工作任务的基本要求,规划机器人驱动关节的运动轨迹,实现在约束条件下关节转角的位移、速度以及加速度的连续[3]。根据机器人实际的工作任务需求,在满足机器人工作性能的条件下,生成一系列包含姿态和位置信息的动作序列,组成轨迹离散数据库。在关节空间轨迹规划领域,对于轨迹插值,插值点的选取与样条曲线的阶次会影响最终样条曲线的特征,插值点分布不均则会导致结构运行不连续。TONDU、EL-ZORKANY[4]运用平滑的折线段代替多项式插值,进行轨迹插值,达到降低轨迹中间点数量的目的。此方法由于缺少插值点,导致关节的运动轨迹精度较差。曹成涛等[5]运用散乱节点的方法确定轨迹插值点,运用于机器人轨迹规划中,达到平滑运动轨迹的目的。
本文作者首先通过PH曲线平滑处理机器人动平台的门字形轨迹的直角拐角,设定轨迹时间后,对机器人的时间-主动杆关节转角所组成的离散数据库进行轨迹压缩,获得保留轨迹特征的最优离散数据点。利用5次NUBRS曲线,进行轨迹插值,得到关节角度、角速度、角加速度曲线。与按时间均匀划分所得相同数目的轨迹数据点作为插值点,进行轨迹插值后数据的对比。利用联合仿真与实验,通过控制并联机器人各个主动杆转动角度,实现动平台运动轨迹的可视化,验证此方法能否有效实现运动的平稳性。
1 Delta机器人末端拾放轨迹优化
Delta机器人由动平台、静平台和3条相同支链组成。每条支链都由主动杆与从动杆组成,机构简图如图1所示。
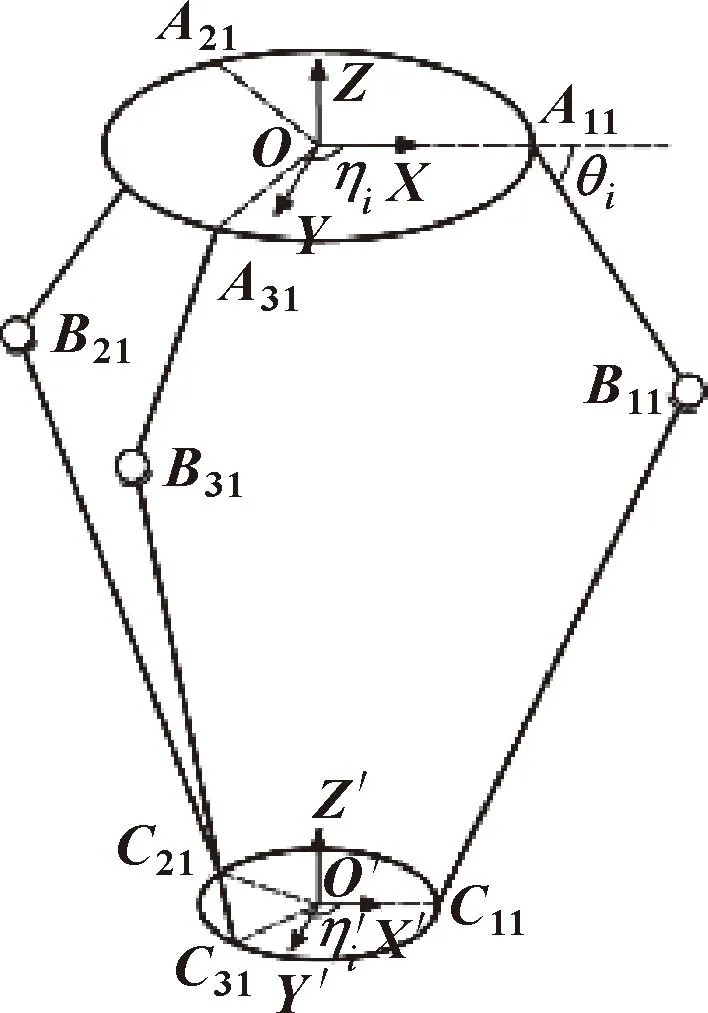
图1 Delta机器人的机构简图
在实际生产生活中,Delta机器人主要实现对物体的拾放操作,末端动平台的常见运动轨迹为包括竖直、水平、竖直轨迹3个部分的门字形轨迹。由于竖直与水平方向轨迹的连接处存在直角拐角,当机器人处于高速运动状态下,速度与加速度发生突变,结构易产生冲击、振动,降低机器人使用寿命。为使动平台按照门字形轨迹运行时更加平滑,采用曲线过渡直角拐角的方法优化此拾放操作轨迹。对于直角过渡处,许多学者通过椭圆弧、拉姆曲线或者其他曲线完成对轨迹的平滑设计,达到平稳扭矩、降低残留振动的目的,提高机器人的工作效率。
PH 曲线作为一类特殊的贝塞尔曲线,曲率连续变化、曲线平滑,其长度和曲率均可通过有理表达式表示,便于计算与应用。基于以上优点,选取3次PH曲线对常见门字形轨迹的直角过渡处进行平滑处理[6],如图2所示。
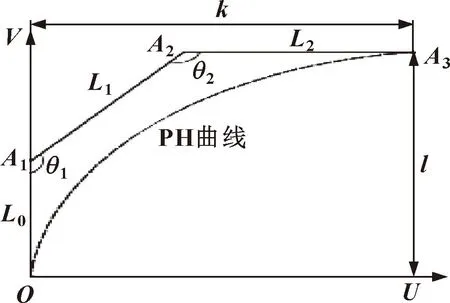
图2 PH曲线及坐标系
3次PH曲线表示如下:
τ∈[0,1]
(1)
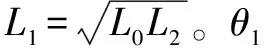
参数化表达式为
P(τ)=P0(1-τ)3+3P1(1-τ)2τ+3P2(1-
τ)τ2+P3τ3
(2)
PH曲线上各点坐标表示如下:
(3)
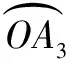
(4)
运用PH曲线对门字形轨迹的直角拐角处进行过渡平滑处理,根据机器人实际工况确定最终的轨迹信息。确定机器人在传送带拾取物体的区域,已知Delta机器人的有效工作空间,首先确定传送带与机器人静平台的竖直距离,明确机器人在传送带的有效工作区域,选择传送带上合理的拾取区域为一长方形。将拾取区域划分成2 mm×2 mm的正方体网格,如图3所示,以每个网格的中心坐标为并联机器人拾取物体的起始点坐标。根据物体拾取位置坐标点和物体放置坐标点,绘制一个竖直平面,经过这两点,在此平面内形成一个优化的门字形路径轨迹。将轨迹的原始数据点通过压缩,形成稀疏的轨迹离散点,作为离线数据储存在机器人的数据库中。每一个网格都存储相关的轨迹离散点。图3中左右两个正方形表示机器人末端动平台放置物体的中心位置。当机器人末端用于对小型食品的拾放时,放置点的位置在空间中竖直方向低于拾取点的位置,由此作者选择拾取点与放置点距离最远的轨迹拾取点进行计算与仿真实验。Delta机器人末端动平台运动轨迹如图3所示。6个轨迹点的三维坐标分别为P0(0,200 mm,-620 mm),P1(0,200 mm,-590 mm),P2(18 mm,191 mm,-550 mm),P3(382 mm,9 mm,-550 mm),P4(400 mm,0,-590 mm),P5(400 mm,0,-670 mm)。
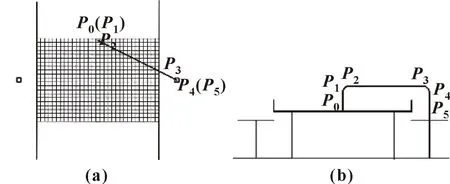
图3 传送带有效拾放区域与典型轨迹的俯视
2 轨迹数据处理
2.1 同步欧氏距离
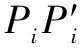
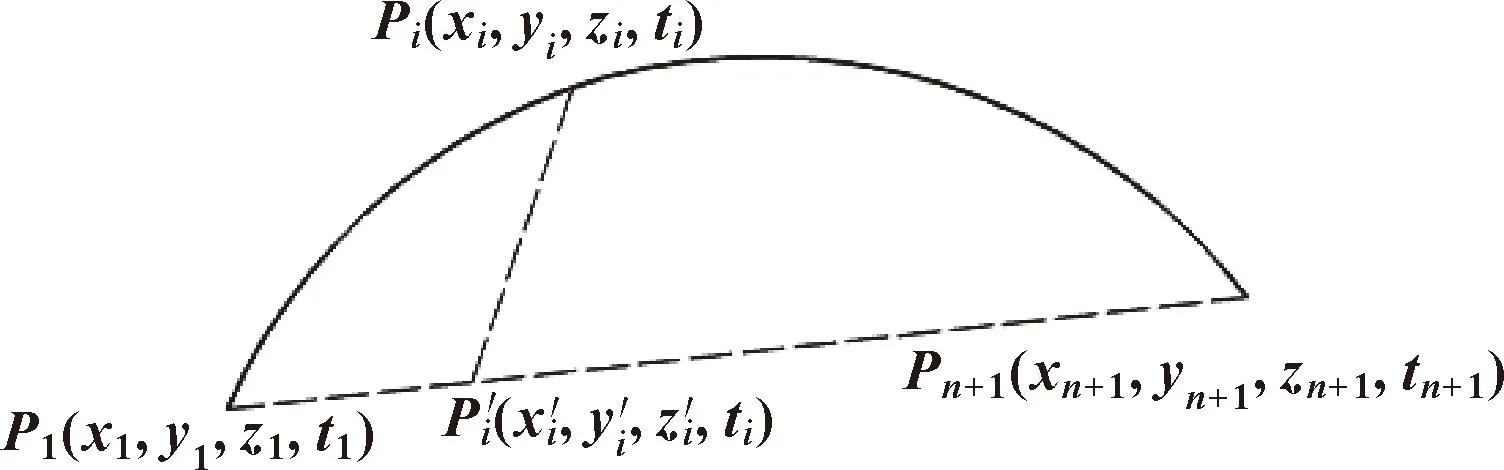
图4 同步欧氏距离
公式如下所示:
(5)
其中:
2.2 轨迹数据压缩
通过对机器人结构中末端移动平台的运动轨迹的划分与压缩,提高轨迹数据处理与数据特征提取的效率。根据机器人运动轨迹的特点提出了基于时间与空间特征的压缩方法。机器人末端动平台的运动轨迹在本质上是连续的,但采集、存储和处理技术使得实验只能通过离散的轨迹数据实现对物体运动过程的描述与研究。机器人离散轨迹数据较多,在保证机器人尽可能多的有效轨迹信息的前提条件下,对移动对象的轨迹数据进行压缩处理,提取出有价值的位置信息。在节约存储空间、便于存储的同时,可以减少轨迹数据数量,便于数据的传输;而后便于对动平台的轨迹数据进行深入分析与后续的轨迹插值[7]。
轨迹数据包含轨迹的位置信息与时间信息。由图3可知,将优化后的机器人末端轨迹划分成直线上升段P0P1、曲线上升段P1P2、直线水平段P2P3、曲线下降段P3P4、直线下降段P4P5五段轨迹后,将笛卡尔坐标系下轨迹三维坐标点依次代入反解程序,得出3个主动杆的转动角度,以3个主动杆的转角表示动平台运动轨迹点,继而对机器人的关节空间角度轨迹进行轨迹压缩分析。
2.2.1 轨迹数据压缩方法
由于轨迹离散数据点已知,选用离线压缩方法处理更为合适。采用自顶向下算法,即TDTR算法。通过比较轨迹离散点的同步欧氏距离与压缩阈值大小,进行递归计算。方法计算复杂度较高,为O(n2) ,但其同时考虑空间与时间两大特性,能较好地保证轨迹的时空特征,压缩结果较好[8]。对于当前轨迹压缩算法,需要用户预先设置同步欧氏距离的压缩阈值,才能实现轨迹数据的压缩。根据最终压缩结果的不同要求,需要通过大量的实验不断确定压缩阈值的较优值。
考虑轨迹数据中的时间因素,由于轨迹运动周期时间短,设定最终压缩得出的相邻轨迹特征点的间隔时间介于10~20 ms之间;然后以同步欧氏距离对原有的TDTR算法进行改进,消除轨迹压缩阈值的约束条件,以轨迹压缩的后相邻两数据点的时间间隔介于10~20 ms的阈值为要求,进行轨迹压缩。
压缩误差为轨迹中非特征点到相邻特征点连线的平均距离,计算公式如下:
(6)
式中:lk为非特征点k到两端相邻最近的特征点的距离之和;M1为压缩前的数据点个数;M2为压缩后的数据点个数。
前期预处理中,将各段轨迹的关节弧度按长度与时间均分为n段,得到n+1个轨迹数据点,作为轨迹压缩的前期样本数据。具体步骤如下:
步骤一,导入样本数据点后,求解轨迹数据离散点中除起止点之外所有数据点的同步欧氏距离lTESD,i(i=1,2,…,n)。
步骤二,判断步骤一中轨迹采样点之间的时间间隔是否都满足时间的阈值要求,如果满足要求,则直接输出轨迹采样点、压缩误差信息;否则就继续下一步骤。
步骤三,以最大同步欧氏距离的采样点为界限将此轨迹划分为两段,再将两段轨迹中的离散采样点作为样本数据点分别代入步骤一中继续压缩,实现对轨迹压缩数据的提取。
改进的TDTR算法流程如图5所示。
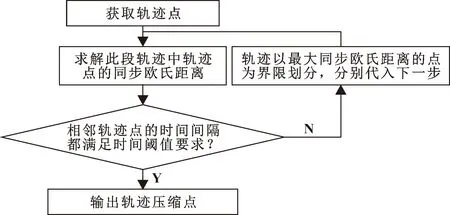
图5 改进的TDTR流程
TDTR-GA是将智能算法中遗传算法与改进的TDTR轨迹压缩算法结合,实现轨迹划分段数的寻优。为评价轨迹压缩的准确性,达到最大程度保留轨迹特征的要求,根据改进的TDTR算法对原始离散轨迹进行压缩。给定轨迹所需时间,通过对初始运动轨迹的划分,实现对轨迹压缩误差的单目标优化。优化模型如下:
f=min(E)
(7)
进而输出产生的最优压缩误差的初始轨迹划分段数n。重新代入改进TDTR算法,最终得出机器人空间中关节的最优压缩轨迹数据点,即轨迹的特征点,以便进行下一步的轨迹插值与轨迹仿真。
2.2.2 轨迹数据压缩实验
明确此次实验的轨迹基本数据,设定各段时间。令P0P1、P1P2、P2P3、P3P4、P4P5各段所需时间分别为t1=0.05 s、t2=0.1 s、t3=0.25 s、t4=0.1 s、t5=0.135 s。压缩后各段所得轨迹数据点数量依次为5、7、17、8、9。汇总后,以3个主动杆的转角为自变量绘制的压缩前后的整体离散轨迹数据点如图6所示。图中q1、q2、q3分别表示机器人3个主动杆的转动角度。
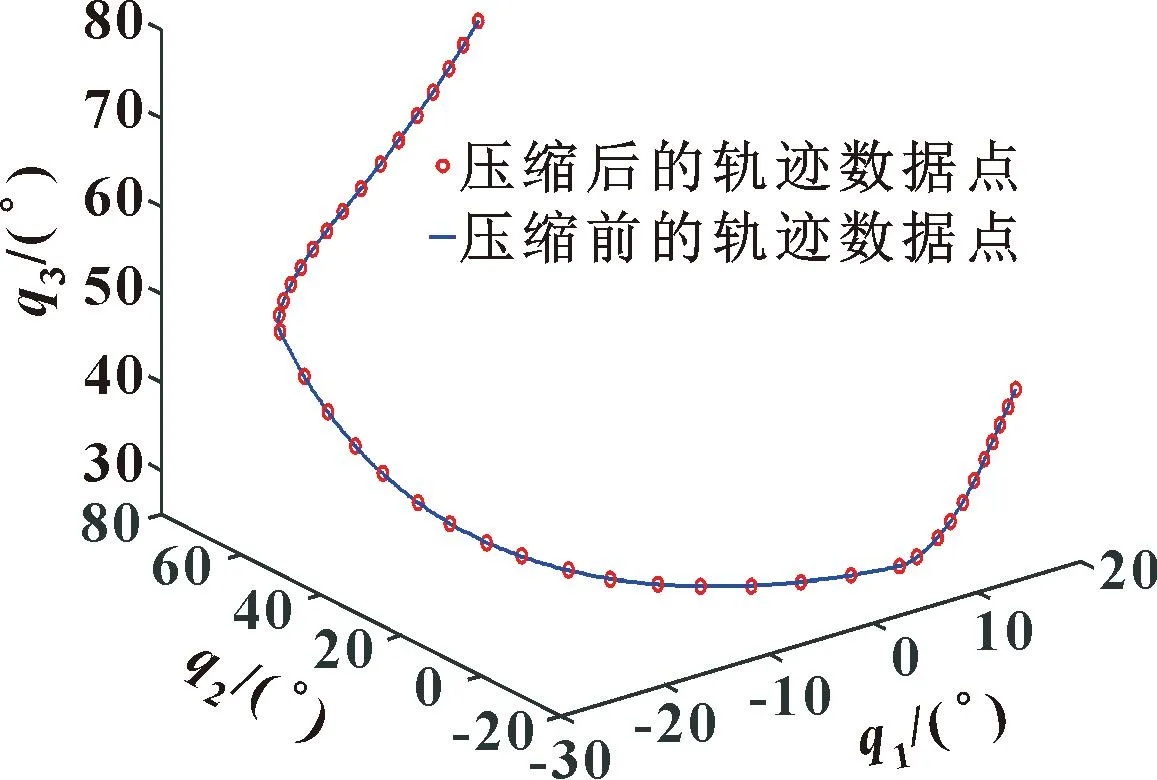
图6 压缩前后的离散轨迹角度点
3 NURBS曲线插补
3.1 NURBS曲线表示
由于前期对并联机器人主动杆的转动角度数据进行压缩处理,以所得的轨迹压缩特征点为插值点,调用 NURBS曲线进行插补,生成一条NURBS 曲线。继而对NUBRS求导,得出该主动杆关节轨迹空间中每一个时间点的角度、速度、加速度值。k次NURBS 曲线函数如下所示:
(8)
式中:u为曲线的控制变量;n为插值点个数;ωi为权因子,并且ω1>0,ωn>0,ωi≥0,(i=2,3,…,n-1);曲线节点向量为U=[u0,u1,…,uk,uk+1,…,un,un+1,…,un+k+1];Ni,k(u)为依据节点向量按照DeBoor-Cox递推公式定义,同时规定0/0=0。
(9)
(10)
文中采用规范节点矢量,令u0=u1=…=um=0,um+n=um+n+1=…=u2m+n=1,并使用累积弦长参数化方法对时间间隔矢量进行归一化得到节点矢量U的元素ui:
在规定0/0=0的前提条件下,m次B样条基函数的k阶导矢为
(11)
式中:
根据上式即可求解物体运动中不同时刻的速度与加速度,绘制参数曲线[9]。
3.2 插值曲线对比试验
将第2.2.2节中轨迹压缩所得的离散轨迹数据点作为插值点,利用五次NUBRS曲线进行轨迹插值,相继求出Delta机器人各个主动杆关节角度、角速度和角加速度如图7所示。
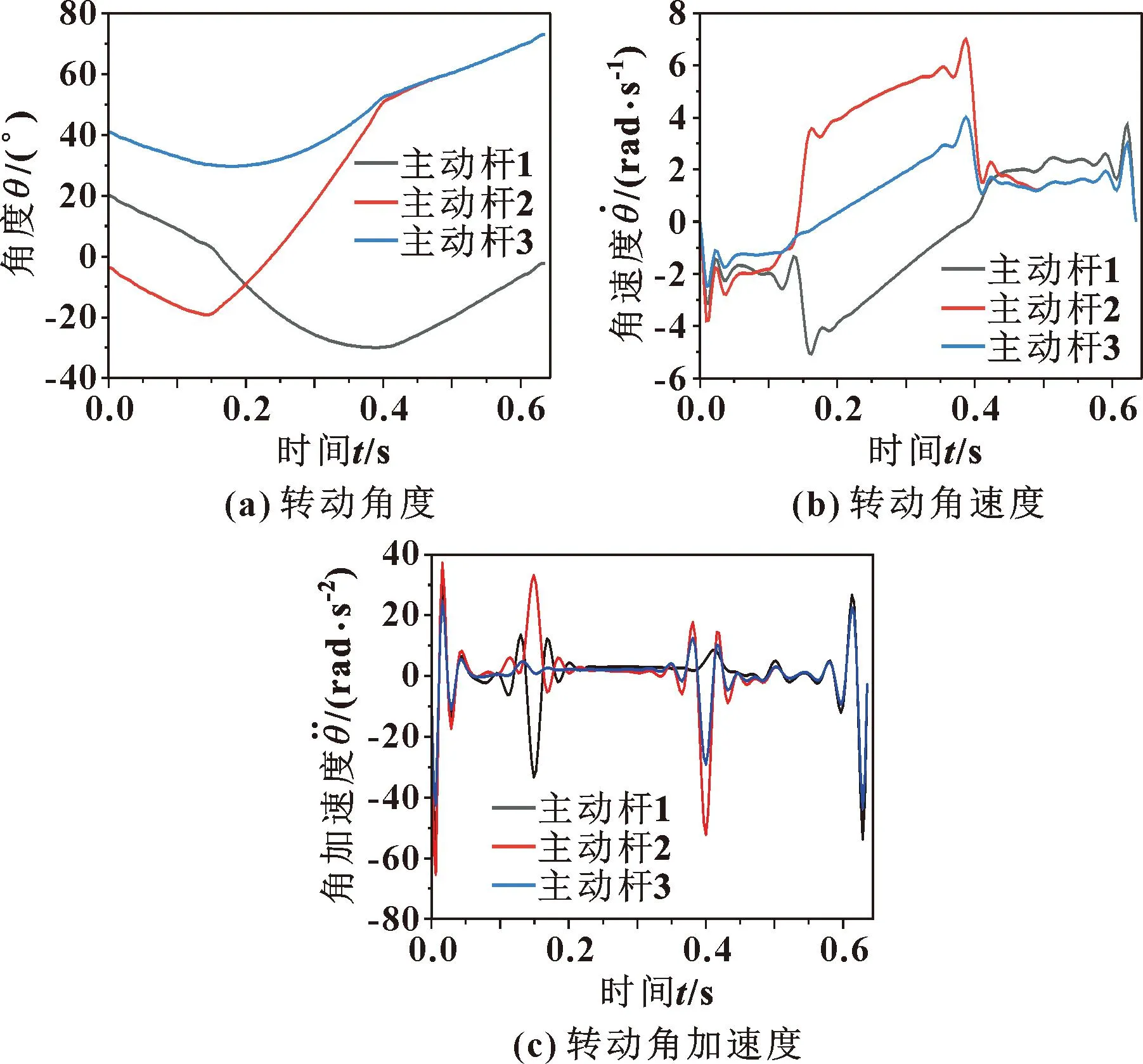
图7 轨迹压缩后的机器人主动杆运动曲线
根据前期各段轨迹数据压缩后所得离散轨迹数据点的数量,将轨迹数据按长度与时间进行均匀划分,生成同等数量的轨迹离散点作为插值点,采用五次NUBRS样条曲线进行轨迹插值,最终得出Delta机器人的各主动杆关节的角度、角速度、角加速度曲线如图8所示。
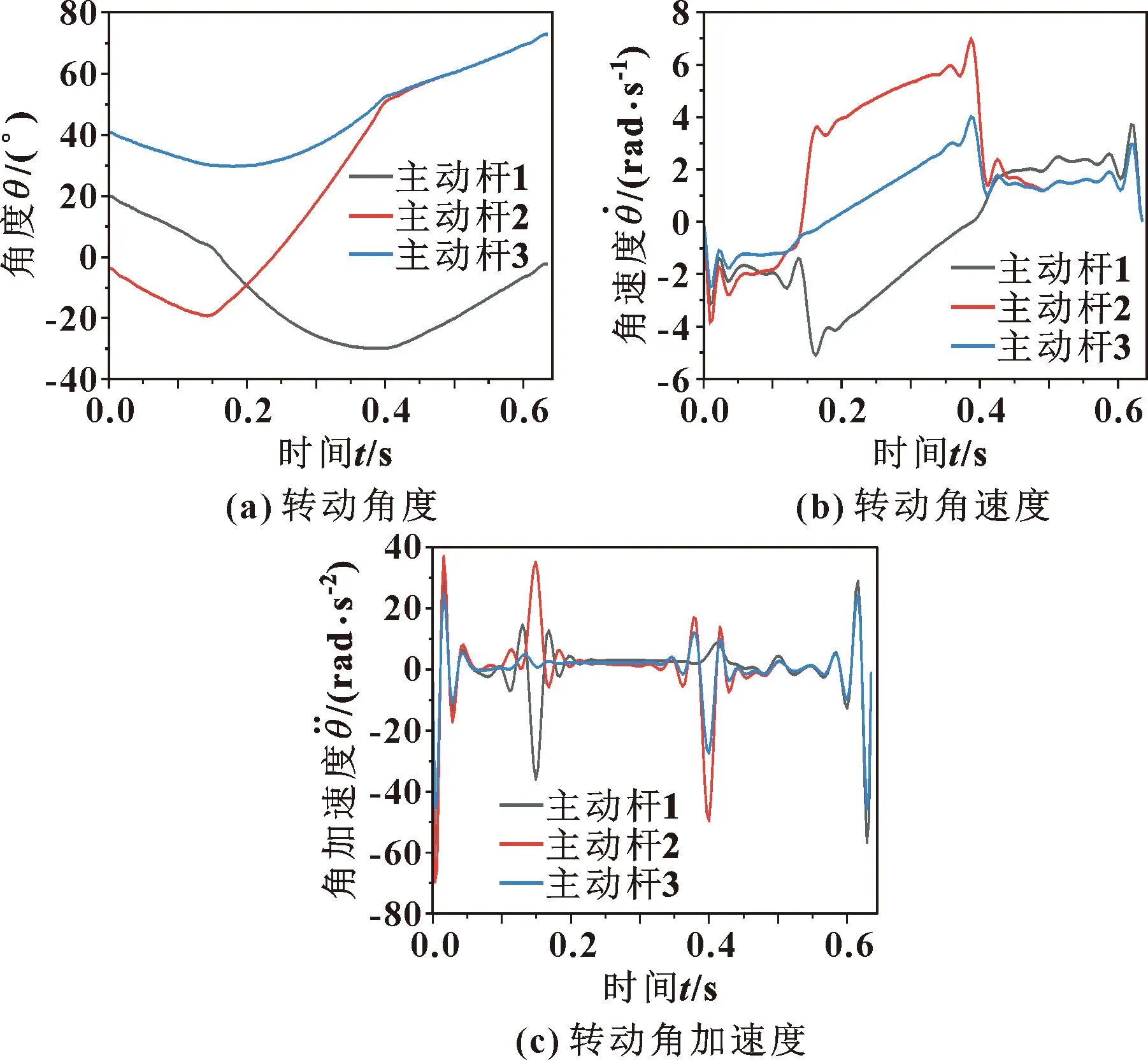
图8 轨迹均匀划分后的机器人主动杆运动曲线
速度方面,图7(b)中各主动杆的角速度最大数值分别为5.08、6.99、3.94 rad/s;图8(b)中各主动杆的角速度最大数值依次为5.10、6.96、4.00 rad/s。相比于均匀划分轨迹,应用轨迹压缩方法得出的数据点,主动杆1与主动杆3角速度最大值分别下降0.4%与1.5%,主动杆2则上升0.4%,且各角度曲线的极差分别下降1.1%、0.5%、1.3%。
加速度方面,分析图7(c)与图8(c),比较机器人主动杆转动角加速度的最大数值与极差。主动杆1的角加速度最大时间点与极差时间段位于周期前0.05 s内,轨迹数据压缩相对于轨迹均分,两值分别缩小4.32%、1.82%;主动杆2的角加速度最大数值的时间点与极差时间段位于周期前0.05 s内,轨迹数据压缩相对于轨迹均分,两值分别缩小6.02%、3.14%;主动杆3的角加速度最大数值时间点与极差时间段位于周期中最后0.05 s内,轨迹数据压缩后相对于轨迹均分,两值分别缩小5.08%、6.06%。
通过图中数据分析与对比发现,利用轨迹压缩方法得出的离散数据点作为插值点,插值后所得的角速度与角加速度在整个周期内更加平稳,减缓驱动电机的转动速度变化,提高寿命,证明了运用轨迹压缩获取插值点方法的可行性和优越性。
4 仿真与实验
4.1 MATLAB与ADAMS联合仿真
ADAMS作为机械系统仿真软件,利用此软件可实现机器人复杂运动过程的仿真。采用ADAMS与MATLAB/Simulink联合仿真对并联机器人的各个主动杆转动角度进行控制,实现对机器人结构中移动平台运动轨迹的仿真,实现末端动平台轨迹的可视化[10],获取整体运动性能,为后期控制算法提供依据。
将Delta机器人的三维简化模型导入ADAMS软件中,对机械结构中相互接触的零部件添加连接方式,在机器人各个主动杆转动副的关节转动角度添加状态变量。令各个主动杆转动副的关节转动角度为输入变量,令动平台几何中心的坐标点为输出变量。利用ADAMS中的Controls模块将虚拟样机机械系统转换成MATLAB/Simulink中子系统模块[11]。建立各输入、输出数据之间的联系,实现 ADAMS 与 MATLAB 的数据的实时交互传递[12]。MATLAB/Simulink中子系统模块如图9所示。
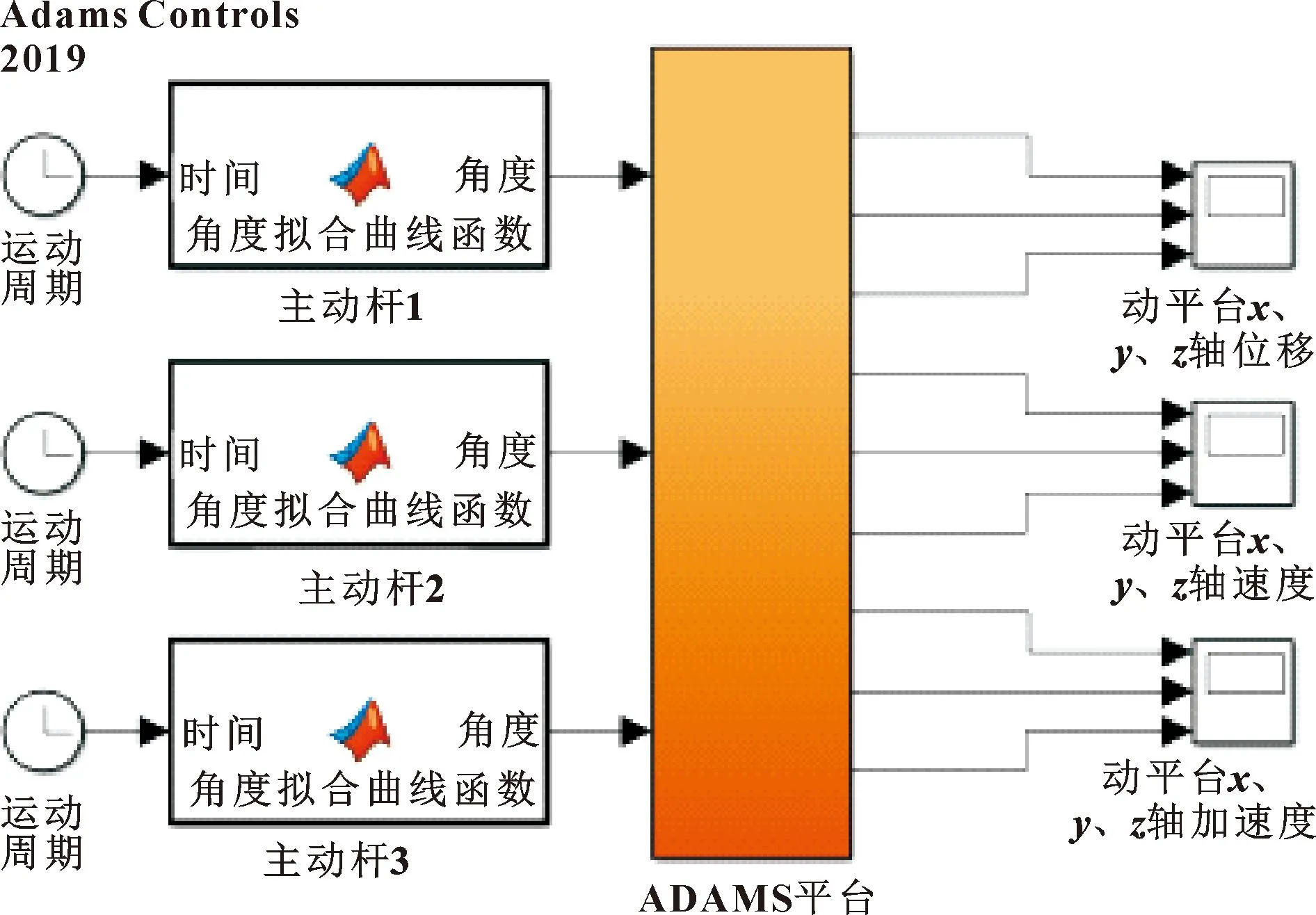
图9 MATLAB/Simulink的子系统模块
将前期在MATLAB中根据轨迹插补得出的机器人各主动杆的两组时间-转动角度数据分别进行拟合,得出曲线函数,代入各自模块,得出在规定时间内动平台的运动轨迹、运动速度与加速度。Simulink中求解器显示机器人末端动平台的位移、速度及加速度的仿真曲线。两组数据中动平台的加速度曲线对比图如图10所示。
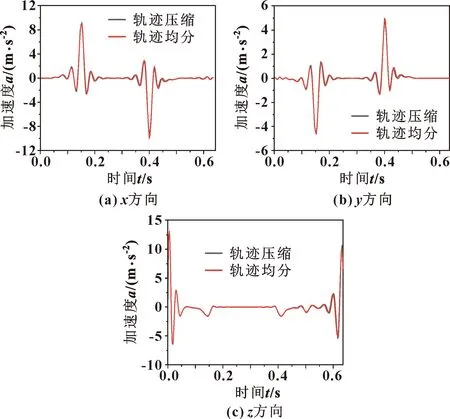
图10 轨迹压缩与轨迹均匀划分的机器人动平台加速度曲线对比
通过ADAMS与MATLAB对机器人联合仿真。由于轨迹周期相同,对比最大加速度。轨迹压缩相比均匀划分的加速度最大值,x方向下降2.32%,y方向下降2.70%的,z方向则下降0.9%,动平台运动较稳定。仿真验证轨迹压缩理论有效性的同时实现了机器人动平台运动轨迹的可视化。
4.2 实验
为验证机器人按轨迹压缩点运行的运动性能,搭建如图11所示的Delta机器人实验平台。

图11 Delta机器人实验平台
此实验平台选用台达通用伺服电机ECM-B3M-CA0604SS1,驱动器的型号为ASD-B3-0421-E,运动控制卡为固高GE400。样机中收集加速度数据采用的加速度传感器为维特智能公司的WT901C485九轴姿态角度传感器,稳定性极高,数据传输稳定,传输距离较远。通过电机控制各主动杆的转角与离散的轨迹压缩点吻合,测量动平台的加速度如图12所示。
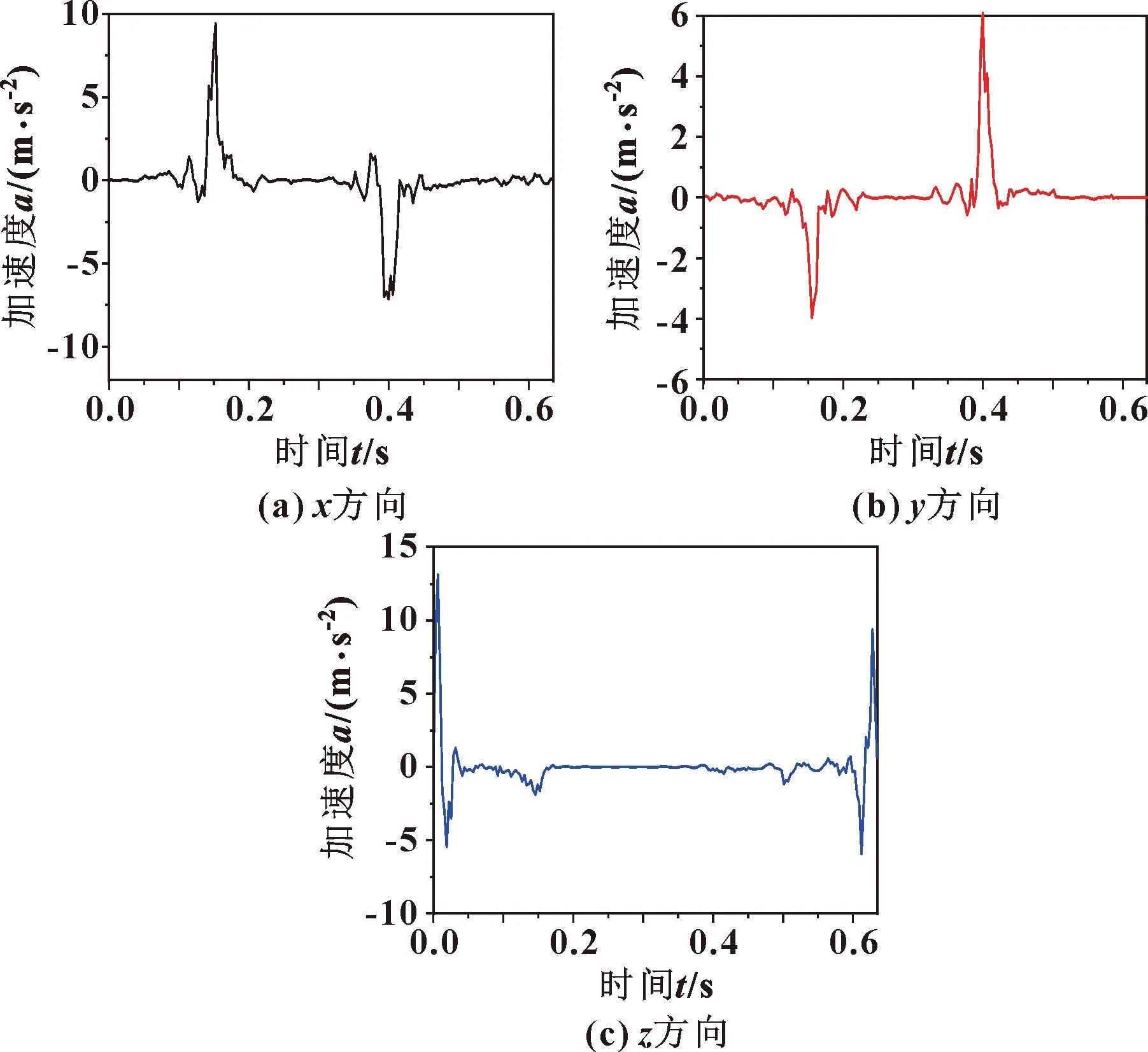
图12 机器人实验动平台加速度
由图12可知机器人动平台在空间坐标系中的加速度。与图10中采用轨迹压缩方法的仿真曲线对比,发现动平台在空间坐标系x、y、z方向上加速度变化规律一致,且数值在一定范围内不断波动,这是由于机器人结构的所选材料具有弹性、关节连接处存在的间隙导致。仿真与实验对照,动平台沿x方向运动加速度最大数值处的时间吻合,数值误差为0.443 m/s2,沿y方向加速度最大数值处的时间吻合,数值误差为1.394 m/s2,沿z方向加速度最大数值处的时间吻合,数值误差为1.21 m/s2,均处于可控范围之内。
结果证明基于轨迹压缩进行轨迹数据点的选取方法对于实现机器人平稳运动的有效性,验证仿真模型正确性的同时保障拾取物体的速率可达50 次/min。
5 结论
对Delta机器人进行轨迹优化,采用PH曲线平滑过渡动平台门字形轨迹的直角拐角。通过遗传算法与改进的TDTR算法的结合,进行轨迹离散数据的压缩处理,获得有效保留关节轨迹的曲线特征的最优轨迹特征点。采用五次NUBRS样条曲线以特征点为插值点进行轨迹插值,获得关节的转动角速度与角加速度曲线。与按时间均匀划分所得相同数目的轨迹数据点作为插值点进行轨迹插值,相关参数对比表明:采用轨迹压缩算法的轨迹插值方法具有降低速度与加速度的最大值与极差的优点,在提高运动平稳性方面具有明显优势。最后通过联合仿真与测试实验实现了机器人优化轨迹的可视化,结果表明,采用此轨迹方法,机器人动平台运动更加平稳,循环拾取操作的速率可达50次/min。
