基于全局能量优化的液压机械臂节能控制策略
2023-12-20张啸甫施光林
张啸甫,施光林
(上海交通大学机械与动力工程学院,上海 200240)
0 前言
液压机械臂常应用在一些需求大功率、高承载力的应用场合,如农林、矿业、工程施工等领域[1-2]。由于液压系统具有高功率密度比、高响应速度、大扭矩输出等优点,使得液压机械臂在上述领域内得到了广泛的应用。
传统通过手动控制多路阀实现液压机械臂各关节运动的开环控制方式会造成很大的能量损失,另外一些采用闭环控制的先进液压机械臂由于大多数情况下采用了阀控系统,也存在着较大的节流能量损失。由于在许多工业系统中,特别是在特殊应用场合下,与其他性能要求相比,能源效率一般成为次要的设计目标。然而,由于液压机械臂常应用在行走式机械中,所携带能源的空间是有限的。因此如何降低能量消耗的同时,不以牺牲控制性能为代价,是液压机械臂面临的一个重要挑战。
一般来说,影响液压系统能量效率的能量损失主要有3种类型:机械损失、容积损失以及阀的节流损失。有学者提出利用泵控系统来代替阀控系统,即利用变量泵直接控制液压执行器,通过改变泵的排量实现负载匹配[3-4],或者利用伺服电机驱动定量泵作为动力源,通过改变伺服电机的转速实现泵输出流量的改变。虽然泵控系统具有更高的能效,并且可以大大简化系统的动态特性,但是泵控系统的动态响应要慢得多,控制精度也比阀控系统低。液压系统另一种比较常用的节能方式是采用负载敏感系统(LS),特别是在移动式液压机械臂平台上。LS系统通过负载敏感阀感应负载的压力或者流量变化,控制变量泵的斜盘倾角从而改变泵的出口流量实现负载匹配,以达到节能的目的[5-6]。对于液压机械臂这种多执行机构来说,也有学者提出对每个液压缸采用进出口独立控制方式(SMIMO),对液压缸的进出油口分别使用多个两通阀来进行压力或流量独立控制,使得两腔的压力或者流量与负载尽可能匹配,从而降低能耗[7-8]。除了降低液压系统的能量损耗,通过蓄能器等装置实现液压机械臂运动时势能以及制动能量回收,也可以进一步提高系统的能效[9-10]。上述的节能策略大多是在液压执行层级上实现,而忽视了液压机械臂运动规划上的能量优化。
本文作者将根据液压机械臂关节运动与液压系统的动态特性,建立基于液压系统能量消耗与运动时间的多目标函数,通过优化算法实现系统的全局能量优化的节能控制策略。
1 液压机械臂模型分析
本文作者研究的一款液压机械臂如图1所示。该型液压机械臂具有5个自由度,其中每个关节均由单独的比例阀控制液压缸进行驱动,且各关节位置由绝对式编码器与位移传感器采集,液压缸两腔均有压力传感器反馈压力信息。动力系统由一套伺服电机与定量泵组成,可通过调节伺服电机转速实现流量调节。

图1 液压机械臂结构
1.1 关节与液压缸之间的力、运动转换
图2为液压机械臂单个驱动关节示意,关节的运动状态将由液压缸的伸缩运动来实现,求解关节运动与液压缸运动之间的映射关系是后续工作的前提。对于第i个关节(i=1,2,…,5),根据几何关系可以得出液压缸的伸缩长度为

图2 液压机械臂单关节结构
(1)
式中:yi0为液压缸首尾铰接点O2O3的初始长度;ci、li分别为铰接点O1O2、O1O3的长度;转角βi=θi+Δθi0,Δθi0为关节初始构型角度。
对上式求导,可以得到液压缸的伸缩速度为
(2)
进一步地,可以得到液压缸的加速度为
(3)
同时,关节所需要的驱动力矩由图2中的Fci实现,根据图中所示几何关系,可以计算当前位置的驱动力矩τi为
τi=liFiy=liFcisinγi=J2iFci
(4)
式中:Fci为液压缸负载力;Fiy为液压缸垂直于连杆方向的分力;γi为液压缸与连杆之间的夹角,该角度可以通过以下几何关系求得:
(5)
根据式(1)—(5),在已知各个关节的运动与受力情况下,可以求出对应驱动液压缸的运动与负载情况,从而实现液压缸的控制。
1.2 液压系统动态特性
以第i个关节对应的第i根液压缸为例,液压缸两腔的压力动态方程可以表示为
(6)
式中:pi1、pi2分别为液压缸无杆腔与有杆腔的压力;pil为液压缸两腔的压差;Vi1、Vi2分别为液压缸两腔的容积;Ai1、Ai2分别为无杆腔和有杆腔的有效作用面积;βe为液压油的有效体积模量;Ct为液压缸的内部泄漏系数。qi1、qi2为液压缸两腔的流量,根据流量与压力关系,液压缸两腔的流量可以表示为
(7)
式中:pis、pir分别为机械臂液压系统的供油压力与回油压力;kq为阀的流量增益系数;xvi为阀芯位移。
对于液压系统来说,由于通常情况下系统的频宽远远小于比例阀的频宽,可以近似地认为阀芯位移与控制电压之间为比例关系[11],即满足关系式xvi=kvui。
为了求解关节力矩映射到液压缸的输出力,根据牛顿定律,液压缸活塞杆的力平衡方程可以表示为
(8)
式中:bi为黏性阻尼系数;mci为第i根液压缸活塞杆的质量。考虑到液压缸活塞杆质量小,所产生的惯性力相比较机械臂本体的重力与负载来说几乎可以忽略不计,同时为了简化系统模型,结合映射关系式(1)—(3),上式可以进一步改写为
(9)
液压机械臂单个关节的非线性模型由上述关系式描述,建立控制电压与关节运动的映射关系。
2 关节轨迹插值
为了后续优化目标函数的建立,需要从末端执行器路径中设置一定的途径点,然后通过逆运动学得到关节空间相应的位置,并通过插值函数在关节空间中生成轨迹,同时考虑机械臂关节的运动学和动力学上的边界限制。为了保证轨迹起始点与末端点的速度、加速度、加加速度可以任意配置且光滑连续,使用非均匀有理B样条来获得沿几何路径轴线的归一化运动轮廓的公式。对于给定的关节位置-时间节点序列{pj,tj}(j=1,2,…,f),k阶B样条可通过De Boor公式[12]递归定义为
(10)
式中:p(u)为关节位置;di为控制顶点;u是一个由非递减归一化时间节点组成的向量;n为控制顶点的个数;Ni,k表示B样条曲线的基函数,该基函数表示为
(11)
式中:ui(i=0,1,…,m)为时间节点。由于B样条曲线的性质,插值出的轨迹一般不经过起始点与终止点,为了保证轨迹经过始末点,节点序列u=[u0,u1,…,un+k+1]的两端节点的重复度需要保证为k+1,且控制顶点di的个数满足n+1=k+f+1,时间节点的个数满足m+1=2k+f+1。对节点向量进行归一化处理,归一化后的时间节点矩阵表示为
u=[0,0,…,0,uk+1,…,uf+k-2,1,1,…,1]
(12)
式中的时间节点满足:
(13)
为了保证关节轨迹的加加速度连续且足够光滑,设定B样条阶次为5阶,并通过虚拟点技术将轨迹起始点与结束点的加加速度约束到零。因此在给定控制顶点di(i=0,1,…,n)、时间节点序列u=[u0,u1,…,un+k+1]以及B样条阶次k后,通过式(10)—(13)便可以求解出关节轨迹。但是通常情况下,控制点无法确定,需要根据给定的途径点进行求解。公式(10)确定了f-2个方程,另外需要k+1个约束方程来构成线性方程组对控制点进行求解,这些约束由始末点的速度、加速度、加加速度给出。根据公式(10)确定的轨迹上任意一点的运动学量,可以通过下式进行求解:
(14)

联立式(10)的B样条轨迹方程与约束条件(14),可以得到求解控制顶点的线性方程组为
d=Q-1p
(15)
式中:
d=[d0,d1,…,dn]T
p=[p1,p2,…,pf-2,v0,vf,a0,af,j0,jf]T
式中:bij分别为根据约束条件(14)求出的各运动学轨迹的首末点表达式的各项系数。
因此,给定关节途经点序列,将时间节点矩阵归一化,明确B样条曲线的边界条件后,根据式(15)求解轨迹的控制顶点,最后将求解的控制顶点与时间节点代入到式(10)(14)中,即可以得到任意时刻的关节位置、速度、加速度以及加加速度。通过以上分析可以发现,通过调整关节途经点序列中途经点位置以及相邻两点之间的时间间隔来改变轨迹。本文作者将途经点的时间间隔作为优化变量,来实现关节轨迹的可调性。
3 全局能量优化问题
3.1 全局能量优化目标函数
为了获得液压机械臂完成指定任务时的全局能量最优轨迹,定义运动时的目标函数为
(16)
式中:S1为时间目标函数,评价整体运动的时间效率,其中Δti为各个关节轨迹途经点的时间间隔,即优化变量,通过调整途经点的时间间隔来改变运动状态;S2为液压系统的平均消耗能量,其中T为总的运动时间,qs为液压泵的输出流量,为恒值,psd是根据液压缸两腔压力动态特性与关节轨迹反解出的最优供油压力,该压力的求解过程如下。

(17)
当液压缸伸出运动时,根据压力流量公式(7)可得液压缸有杆腔流量为
(18)
联立式(17)(18)得到当前运动时刻液压缸有杆腔压力为
(19)
由液压缸的受力平衡方程可知:
(20)
式中:bi为黏性阻尼系数;mci为液压缸活塞杆质量;Fci为液压缸与连杆之间的作用力,可由机械臂动力学求得关节力矩,再由式(4)(5)计算得到。进一步地,可求解液压缸无杆腔压力为
(21)
上式存在着控制输入xvi,在理想条件下,忽略系统存在的扰动,根据液压机械臂数学模型式(6)(7)计算近似的阀芯位移。
进而根据公式(7)得到当前液压缸的理想供油压力为
(22)
同理当液压缸缩回运动时,可得液压缸的理想供油压力为
(23)
由于液压机械臂每个关节的负载情况不一致,并且理想轨迹也不一致,因此需要分别计算每个关节液压缸的理想供油压力,取其中最大值作为整个系统的供油压力,即:
ps=max{p1s,p2s,…,pns}
(24)
考虑到摩擦等扰动影响,并保证系统的安全性,需要将计算的系统供油压力加上一个安全阈值,此时系统的供油压力为
psd=ps+psth
(25)
式中:psth为供油压力安全阈值,需要根据实际的负载情况进行选择,文中选择的阈值范围为1~2 MPa。
3.2 多目标求解
快速非支配遗传算法(NSGA-Ⅱ)是一种求解多目标优化问题的优化算法,由于该算法引入了当前个体被支配个数与该个体支配解的集合这两个参数,降低了非支配前沿面搜索的时间复杂度。引入了基于拥挤度与拥挤度比较算子的密度计算方法,保证前沿面分布的广泛性与多样性;同时使用精英保留策略,提高种群水平,扩大了采样空间[13]。
NSGA-II算法的流程如下所示:
Step1,初始化种群P。根据多目标问题的维度以及约束条件确定初始种群,包括初始优化变量以及其上下边界。其中种群个体的适应度值的计算方式如图3所示,种群个体优化变量即为途经点的时间间隔Δti,不同的时间间隔根据式(10)—(15)插值得到不同的轨迹,并根据式(17)—(25)得到不同的系统供油压力,从而得到每个个体的两个适应度值。

图3 种群个体适应度值计算
Step2,使用基于拥挤比较算子的竞赛选择方法,在父种群Pt上进行交叉和变异操作,创建后代种群Ct,其中t表示种群代数。然后将后代种群及其父代种群相结合产生整个种群Rt。
Step3,快速非支配排序。根据提出的基于约束违背度的Pareto支配,确定所有个体的支配关系,并将整个种群按照支配等级分层。一旦排序完成,将计算所有个体拥挤距离值。种群中的个体是根据支配等级和拥挤距离来选择的。
Step4,采用模拟二进制交叉和变突变率多项式变异的实数编码遗传算法来产生新的种群。
Step5,重复这个过程,直到达到最大的迭代次数。
由于传统NSGA-Ⅱ算法中采用的是定突变率,对于种群搜索来说,变突变率更有利于种群收敛到全局最优值。在迭代开始时,希望更大的突变率来避免种群陷入到局部最优解中,在迭代搜索结束时则希望小的突变率使得分布结果更加精确。因此作者提出一种基于Sigmoid函数突变率的变异算子,其突变率mr的形式为
(26)
式中:tmax为最大迭代次数;c1、c2为调整因子,与始末设定的突变率大小有关。随着迭代次数的不断增加,突变率逐渐减少且光滑连续。
NSGA-Ⅱ算法最终得到一个最优解集(Pareto 前沿),可以通过基于隶属度值的选择方法得到全局最优解。
4 仿真结果与分析
为了验证所提方法的有效性,设置3组节能控制策略,分别如下所示:
节能策略1(C1):文中提出的基于全局能量优化的节能策略,将液压系统的能量消耗与运行时间构成多目标函数进行求解。
节能策略2(C2):传统的规划层级节能策略,将C1的多目标函数代替为一般的基于时间-能量的多目标优化策略,即:
(27)
式中:n为关节个数;θi为关节角度。同时上式求出的轨迹利用式(17)—(24)反解出最优供油压力,控制液压系统。
节能策略3(C3):传统的定供油压力控制方法,轨迹跟踪时液压系统的供油压力保持不变。各个关节轨迹采用C2策略得到的轨迹。
按照顺序分别选取途经点为(1 290,50),(1 432,300),(1 670,630),(1 760,830)(单位均为mm),通过运动学逆解可以得到每个途径点对应的关节构型。C1和C2优化后的最优时间间隔如表1所示。
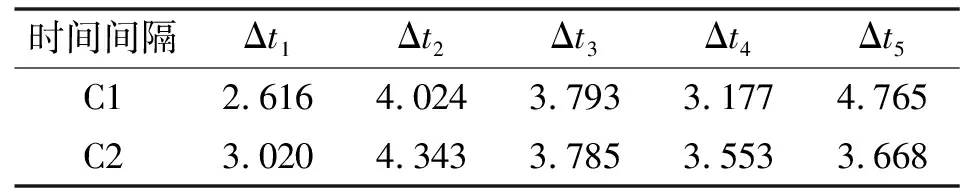
表1 途经点最优时间间隔 单位:s
根据以上条件,液压机械臂在3种策略下的能量消耗如图4所示,其中C1策略较C3策略节约了46.73%的能量,较C2策略节约了8.62%的能量。图5与图6分别为液压系统的供油压力与机械臂末端轨迹情况,可以看出C1策略求解出的理想供油压力最小,末端轨迹也更加平滑。

图4 不同策略下的能量消耗情况

图5 不同策略下的供油压力

图6 C1与C2策略的末端轨迹
C1策略根据各关节轨迹反解出每一时刻液压机械臂系统对应的理论供油压力,从而构造液压层级的能量函数,并将该能量函数引入到规划层级中构造多目标优化问题进行优化求解,从而得到液压机械臂全局最优能量轨迹。反解出的供油压力可以作为可变溢流阀的控制信号,以此控制液压系统的供油压力,从而降低能量消耗。
不难发现C1策略较C2策略节约的能量并不十分明显,这是由于C2策略的优化目标同样包含了能量函数。但该能量函数基于机械结构的关节加速度,并没有考虑液压层级的能量损耗情况。同时由于固定了关节空间的途经点,限制了系统能量的优化能力,后续可考虑将途经点加入到优化目标中,进一步降低能量消耗。
5 结论
本文作者针对液压机械臂存在的能效较低问题,提出一种基于全局能量优化的节能方法,将液压系统的能量消耗函数加入到多目标优化函数中。在得到关节理论轨迹的情况下,根据流量-压力映射关系反推出每一时刻对应的理论供油压力,以此压力计算液压系统的能量函数,并与运动时间构成多目标优化问题。最后通过改进的变突变率的NSGA-Ⅱ多目标优化算法进行求解。通过对比仿真结果可知,在文中工况下,提出的全局能量优化算法与固定供油压力策略相比,节约了46.73%的能量,与传统的基于时间-能量优化的节能策略相比节约了8.62%的能量,从而验证了所提节能策略的有效性,为液压机械臂的节能控制策略研究提供了理论参考。
