高压共轨喷油器系统鲁棒性分析与优化
2023-12-20贠振刚李少年张海丽史瑞静
贠振刚,李少年,张海丽,史瑞静
(1.兰州理工大学能源与动力工程学院,甘肃兰州 730050;2.新疆工程学院能源工程学院,新疆乌鲁木齐 830091)
0 前言
高压共轨燃油系统具有喷射压力高、喷油速率可调的特点,能够独立实现喷油参数的调节而不受发动机工况影响,可有效降低柴油机的排放和油耗,成为当前柴油机燃油喷射系统的主流[1]。由于喷油器连续性供油是影响共轨系统稳定的主要因素,对于具有复杂且动态的电-机-液耦合特性的电控喷油器,优化系统关键参数直接影响喷油器喷射过程,可有效提高控制精度、稳定性、经济性以及环境保护等方面。
目前国内外学者对喷油器驱动器结构、密封特性以及加工工艺等多方面进行了大量研究。KOLESKI、BICKEL[2]通过建立电控CR喷油器模型,采用进化策略优化方法,提高了燃油效率和喷射率控制;SORIANO等[3]建立零维预测性喷油率模型,计算了喷射压力、总燃油质量和喷油速率;汪宇航等[4]运用单向流固耦合的方法证明了组合优化方案提高喷油器密封特性时的良好性;罗福强等[5]通过试验测试计算某大功率柴油机喷油器喷油压力、喷油脉宽和喷孔直径对喷油规律的影响;许文燕等[6]采用正交试验加一维仿真的手段,研究共轨喷油器结构参数匹配问题;刘振明等[7]建立喷油器压电驱动器热-电-力多场试验系统,探究电场和热场下的喷油器喷射规律;徐晓栋[8]采用单因素试验法研究切削速度、进给速度及切削液油压对深孔圆度的影响规律;刘景斌等[9]基于CFD中LES模型,计算分析轨压和脉宽对喷油器球阀处空化影响;兰奇等人[10]基于AMESim计算喷油器的动态响应特性(开启响应时间和关闭响应时间),并运用帕累托探究主要参数对喷油器的影响及影响权重;柯赟等人[11]采用层次离散熵(Hierarchical Dispersion Entropy,HDE),分析参数变化对熵值计算效率的影响,提高了喷油器喷射量的计算精度;张勇等人[12]通过建立数学模型加AMESim计算分析喷油器喷油特性和泄漏特性。
本文作者针对高压共轨喷油器系统鲁棒性,建立复杂喷油器系统的数学模型及AMESim计算模型,基于蒙特卡罗(Monte Carlo)+ 高斯分布方法与拉丁超立方体抽样预测关键参数与喷油器预注入量和主喷射量相关性,分析预注入和主喷射量频率分布特性,并采用NLPQL(Non-Linear Programing by Quadratic Lagrangian)算法对高压共轨喷油器关键结构参数进行优化取最优各因素值,提高共轨系统控制精度和稳定性。
1 电控喷油器系统计算模型
1.1 数学模型的建立
对于电控喷油器系统,主要由压电驱动器、球阀和锥阀三部分组成,当喷油器处于正常工况下,油液经球阀进入锥阀而喷射,各阀容腔内压力方程为
(1)
(2)
(3)
式中:p为阀容腔内油液压力;Qi和Qo分别为阀进、出腔的油液流量;Ql为泄漏流量;A为作用于阀芯端的有效面积;dx/dt为阀芯移动速度;E为油液弹性模量;V为阀腔内容积;μ为流量系数;ρ为油液密度;Δp为阀进出口压差;As为阀内通流面积;d为阀芯直径;δx为阀芯与阀内腔间隙;η为动力黏度;L为阀芯与阀内腔接触长度。
经分析锥阀在压电驱动器、液压力和弹簧力的作用下,其阀芯运动方程为
(4)
m(d2x)/(dt)=Fm+ANpN+Asacpsac-ACpC-
b(dx)/(dt)-ks(xso+xn)
(5)
式中:i为压电驱动电流;N为压电驱动器线圈匝数;Fm为电磁力;φ为磁通量;δ为驱动器工作气隙;μo空气磁导率;S为衔铁有效面积;m为锥阀阀芯质量;AN为锥阀进口面积;Asac为锥阀出口面积;AC为锥阀容腔内有效面积;psac为锥阀出口油液压力;b和ks分别为锥阀弹簧阻尼系数和刚度系数;xso为弹簧预压缩量;xn为锥阀阀芯位移距离。
1.2 喷油器系统计算模型
为分析电控喷油器关键结构参数(进油口孔径、出油口孔径、锥阀阀芯直径、锥阀弹簧预紧力)与预注入量和主喷射量相关性及其频率分布影响,基于多学科计算平台AMESim,运用Electro Mechanical库、Hydraulic Component Design库、Signal库、Mechanical库、Hydraulic库建立系统仿真模型如图1所示,系统模型中进油口孔径和出油口孔径分别由阻尼孔直径A/B模拟,主要参数见表1,各参数参考某型号所用电控喷油器进行设置。

表1 电控喷油器的主要参数
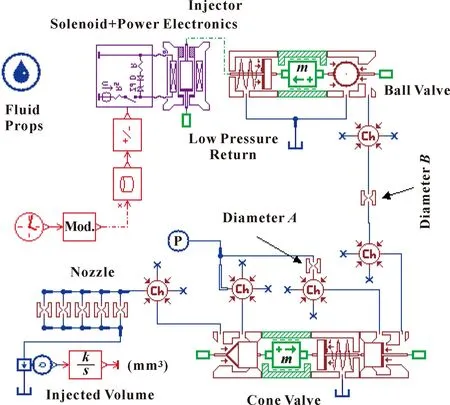
图1 AMESim喷油器系统仿真模型
图2为电控喷油器中电磁力、阀芯升程、流量及体积随时间变化曲线。可知:0.92~1.36 ms为喷油器的预注入过程,当电磁阀充电0.44 ms时,电磁中推杆回移,使球阀阀芯克服弹簧力向左运动打开,其锥阀控制腔油液经球阀泄漏至油箱,此时锥阀控制腔内压力降低导致阀芯向右移动打开,完成喷油器的预注入;2.35~3.28 ms为喷油器主喷射过程,当电磁阀重新充电0.93 ms时,电磁推杆回移使球阀完全打开,锥阀控制腔压力快速减小,致使锥阀完全打开喷油器开始喷油。

图2 电磁力、阀芯升程、流量及体积随时间变化曲线
2 基于蒙特卡罗的喷油器系统鲁棒性分析
2.1 考虑相关性的蒙特卡罗系统分析
为预测多参数不同取值对系统的影响,采用蒙特卡罗方法并满足参数高斯分布方式,其高斯分布基本特征如图3所示,μ表示变量平均值,σ表示变量标准偏差,使该变量所有取值包含于区间[μ-3σ,μ+3σ]。针对电控喷油器进油口孔径、出油口孔径、锥阀阀芯直径、锥阀弹簧预紧力4个关键结构参数进行高斯分布计算,得出各参数取值分布范围分别为[0.27,0.33]mm、[0.17,0.23]mm、 [3.7,4.3]mm、[37,42.9]N。
为评估各关键参数的影响,分析不同参数值与预注入量和主喷射量相关性,选择拉丁超立方体抽样,得到图4—7。观察可知:预注入量与阻尼孔直径A、阻尼孔直径B、弹簧预紧力和阀芯直径有很好的相关性,同时直径A和直径B对主喷射过程影响较大,而弹簧预紧力和阀芯直径与主喷射量的相关性较差。
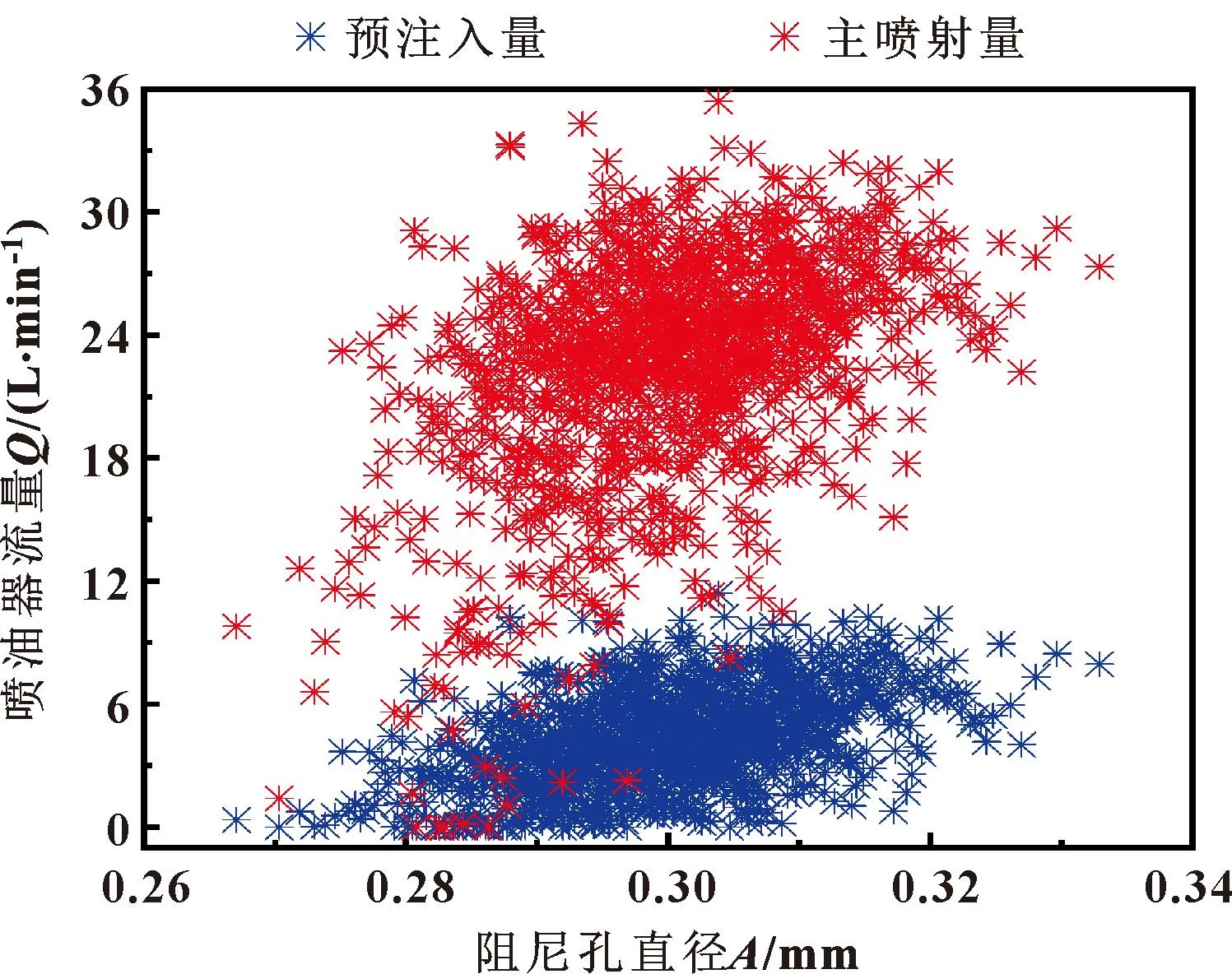
图4 直径A与预注入量/主喷射量散点图分布
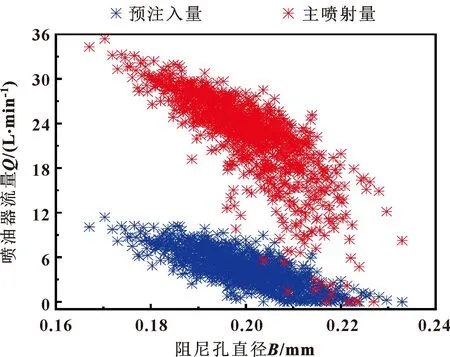
图5 直径B与预注入量/主喷射量散点图分布
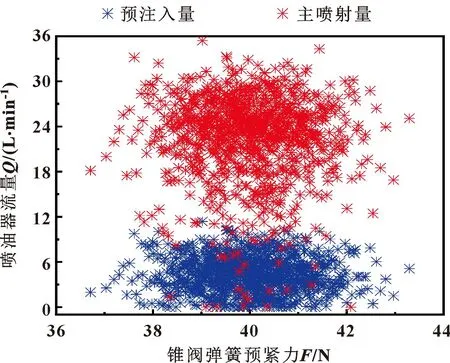
图6 预紧力与预注射量/主注射量散点图分布

图7 阀芯直径与预注射量/主注射量散点图分布
2.2 喷油器系统鲁棒性分析
图8、图9和图10分别为预注入与主喷射的流量、体积以及阀芯升程的频率分布。综合分析可知:主喷射流量比预注入量流量稳定得多,因为频率变化较小,易于控制;相反主喷射与预注入的体积容量稳定性较差,导致很难控制。

图8 预注入与主喷射流量的频率分布
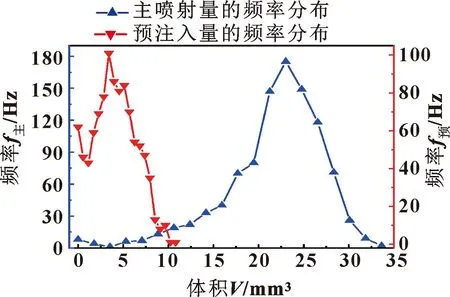
图9 预注入与主喷射的体积频率分布

图10 预注入与主喷射的阀芯升程频率分布
main injection volume
3 基于NLPQL喷油器系统多参数优化
3.1 NLPQL参数优化方法
根据上述蒙特卡罗法对主喷射和预注射量与各参数相关性和频率分布分析,采用NLPQL-SQP序列二次规划法,将带有约束条件非线性问题转化进行参数优化设计,其中把电控喷油器关键参数作为优化变量x(关键参数有进油阻尼孔直径、出油阻尼孔直径、锥阀阀芯直径、锥阀弹簧预紧力),在标定工况下,目标函数f(x)为主喷射量(Q′(x))与喷射量(最大值Qmax(x)或最小值Qmin(x))的方差。并且f(x)取最小值时,得到设计变量的最优解。
带有约束条件非线性规划问题数学表达式[13]为
(6)
式中:x为设计变量;x1为进油阻尼孔直径;x2为出油阻尼孔直径;x3为锥阀弹簧预紧力;x4为锥阀阀芯直径;f(x)为目标函数;ci为约束条件;s为搜索方向。
针对上述式(6)优化问题,将其转化为一个二次规划问题QP[14]:
(7)
式中:B(k)为Hessen矩阵的逼近;αks(k)=x(k+1)-xk,αk为步长因子。
在求解过程中,需判别目标值的收敛性,其判别准则如式(8),当满足判别准则时,则停止迭代[15]。
(8)
约束条件为
(9)
3.2 优化过程与结果
借助 AMESim 中 Design Exploration模块,采用NLPQL算法对电控喷油器系统关键设计参数进行优化,设置相对梯度步长和最终精度分别为0.000 1和1×10-6。图11和图12分别为喷油器系统进油阻尼孔直径A、出油阻尼孔直径B、锥阀阀芯直径d和锥阀弹簧预紧力F优化过程,其各参数优化结果依次为0.316 mm、0.195 mm、3.86 mm、38.44 N,并且迭代次数为36。
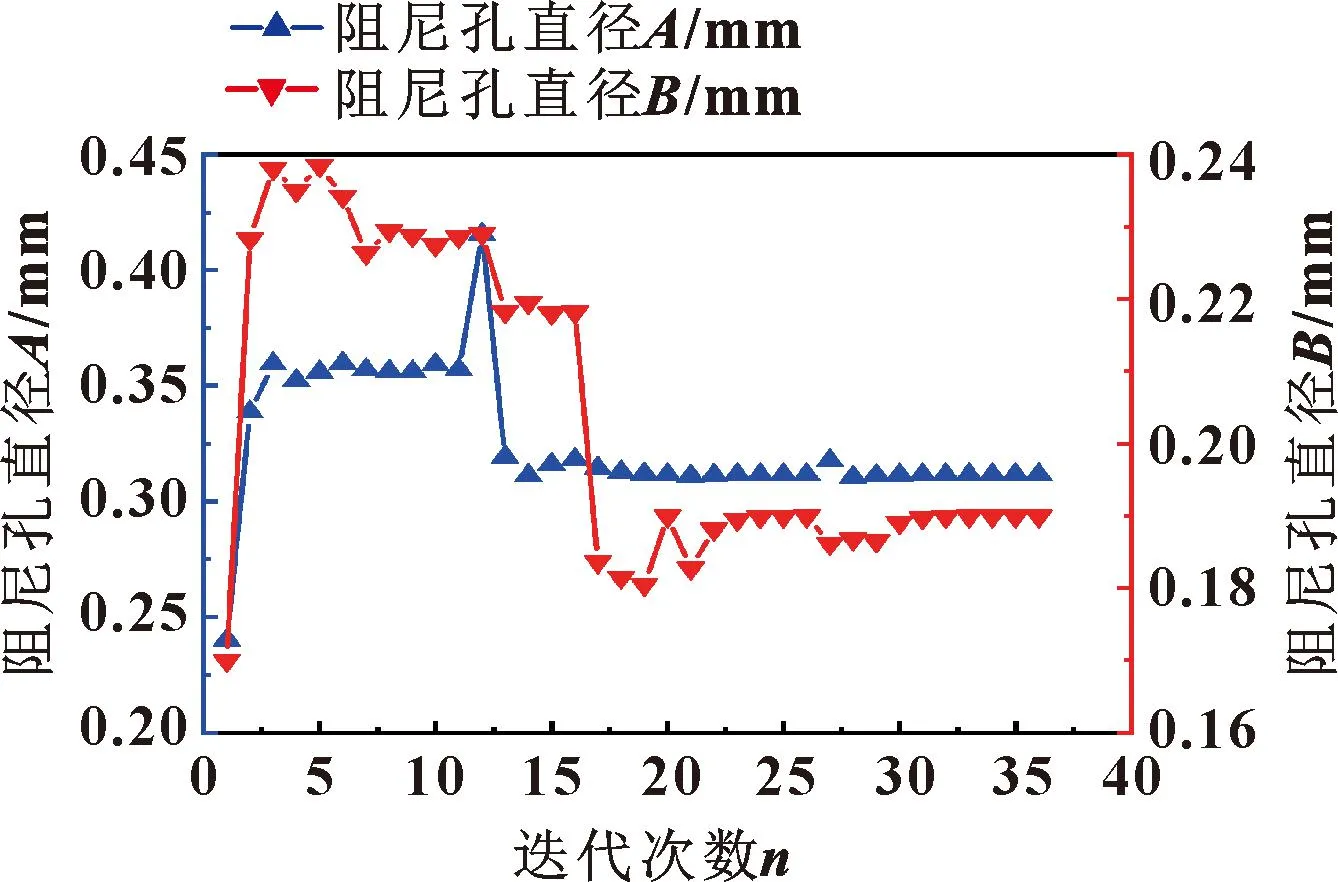
图11 阻尼孔直径A/B优化过程

图12 锥阀弹簧预紧力/阀芯直径优化过程
将上述各参数优化结果导入图1所示喷油器系统仿真模型,得到图13—15。可知:喷油器预注入和主喷射流量各增大10.7%、18.3%,预注入和主喷射容量各增长8.2%、25.6%,预注入和主喷射关闭行程各缩短6.8%、15.9%。由此可见,优化后电控喷油器响应速度提高,增加了喷射器喷射持续时间,使喷油器喷射规律更加理想。
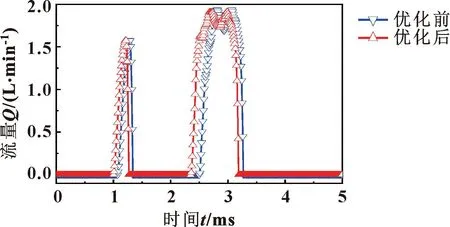
图13 优化前后电控喷油器喷射流量曲线
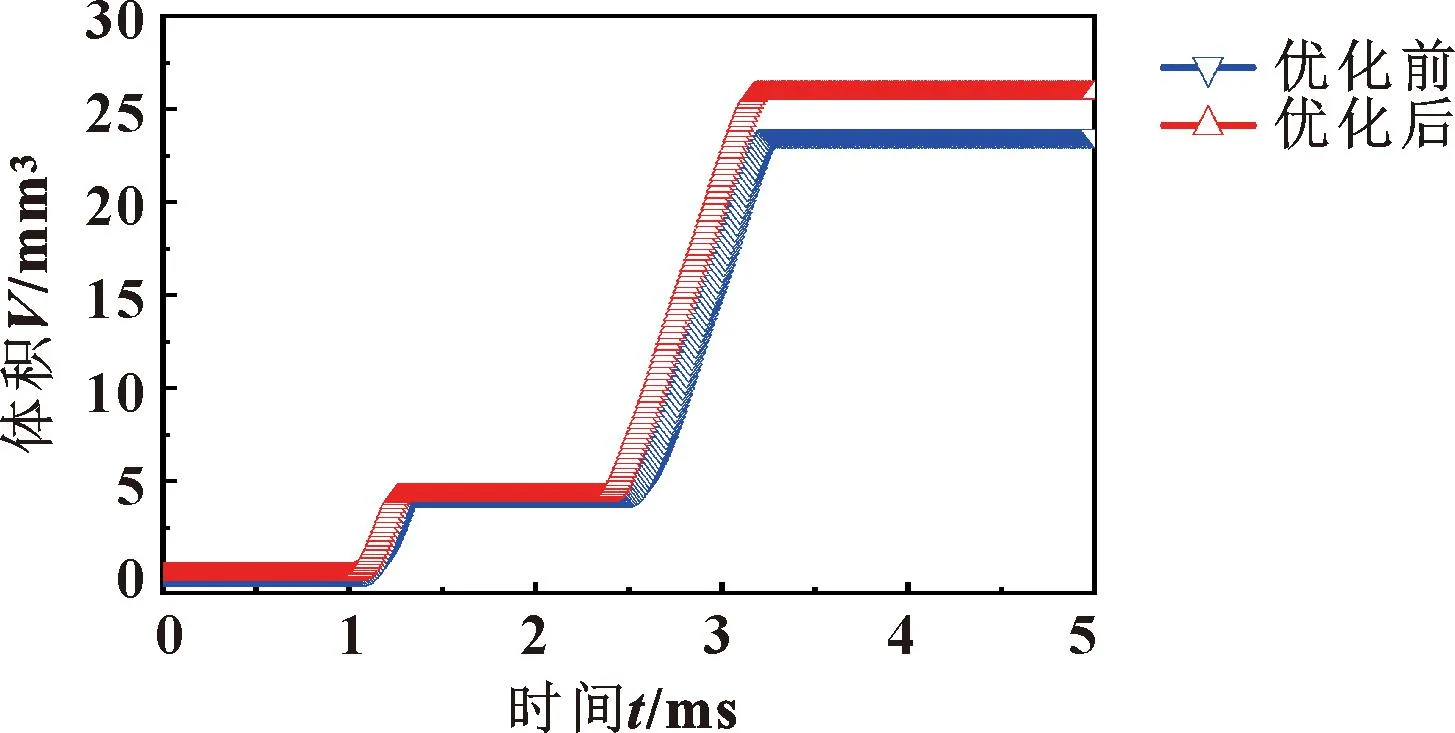
图14 优化前后电控喷油器喷射量曲线

图15 优化前后锥阀阀芯升程曲线
4 结论
(1)经喷油器系统的蒙特卡罗分析,发现预注入量与阻尼孔直径A、阻尼孔直径B、弹簧预紧力和阀芯直径的相关性高,同时直径A和直径B对主喷射过程影响较大。
(2)通过分析预注入及主喷射流量、体积频率分布,得到主喷射比预注入流量频率变化较小,稳定性高,易于控制,而主喷射与预注入容量稳定性较差。
(3)采用NLPQL算法优化进油阻尼孔直径、出油阻尼孔直径、锥阀阀芯直径和锥阀弹簧预紧力,使喷油器预注入和主喷射流量各增大10.7%、18.3%,预注入和主喷射容量各增长8.2%、25.6%,预注入和主喷射关闭行程各缩短6.8%、15.9%。
