高速列车轮轨噪声控制的新型声屏障设计方法研究

2023-12-18张小安曹兴潇朱胜阳杨建近张晓芸

振动与冲击 2023年23期

张小安, 宋杲, 曹兴潇, 朱胜阳, 杨建近, 张晓芸

(1. 兰州交通大学机电工程学院, 兰州 730070;2. 西南交通大学牵引动力国家重点试验室, 成都 610031)

我国轨道交通的高速发展为人们出行提供了极大的便利,但随着站城融合等新发展模式的提出,轨道交通随之所引起的噪声问题也愈加严重[1]。在2022-06-05起实施的新版《中华人民共和国噪声污染防治法》[2]中,对交通噪声污染防治方面也提出了更加严格的要求。因此轨道交通的后期发展有必要开发更加合理高效的降噪装备以及措施。针对噪声敏感地带在线路两侧安装声屏障是目前公认的主要降噪措施[3]。目前我国高速铁路中使用最广泛的声屏障为直立插板式声屏障,占总量的90%以上;在部分高层敏感建筑或有特殊要求的地段则采用隔声性能更优的半封闭、全封闭式声屏障[4-6];但需要关注的问题在于半封闭和全封闭声屏障极大地增加了建设成本。

随着声学超材料的提出,国内外学者则致力于探索声学超材料在声屏障中的应用[7-8]。声子晶体[9-10]是一种针对弹性波具有带隙特性的周期性复合材料或结构,基本特征表现为:带隙频率范围的弹性波在声子晶体中传播时将会受到抑制[11],其中关键原因是由晶体和周围介质组成的周期元素之间的阻抗失配,即当传递的弹性波遇到高阻抗材料时,传播过程中则倾向于增加弹性波在该介质中的相速度;遇到低阻抗介质时,则会减慢相速度,由此可利用阻抗失配元素的周期性排列影响在晶体中传播的声波[12]。由此表明声子晶体能够很好地抑制特定频率范围内声波的传播。有关声子晶体在工程领域的研究,易强等[13]研究了一维周期性声子晶体在声屏障的应用,表明直立式和全封闭式周期性声屏障比同等质量的单一材料声屏障的降噪效果更优。秦晓春等[14]提出了一种声子晶体型高速公路声屏障设计方案,研究表明声子晶体声屏障可以在所需降噪频段内产生相应的完全禁带。王颖[15]提出了一种层状周期性结构在地铁隔振方面的应用,研究表明该结构能够很好地抑制地铁所引起的振动。Huang等[16]引入固体物理的周期理论,研究了周期排桩的衰减特性,通过建立周期排桩插入土体内模型,隔离结构振动证实了周期结构中衰减区的存在,结果表明,衰减区的频率振动可以显著降低。Li等[17]基于声子晶体原理,提出了由一系列混凝土夹杂土壤组成的地震超材料的频散理论,基于多体仿真原理、有限元理论和LS-DYNA的完全匹配层方法,建立了列车-轨道-土体三维耦合模型,从时域和频域的角度分析了在铁路地基中采用该地震超材料的系统振动特性和减振效果,表明地震超材料具有很好的减振效果。

综上所述,为了提升轨道交通声屏障的隔声性能,并且研发更加具有针对不同声源类型的声屏障;本文基于Bragg带隙机理[18]和高速铁路轮轨噪声的主要噪声典型频谱特征[19],建立了三种具有特定带隙特征的气-固型二维声子晶体模型,采用有限元法系统研究了不同排布方式的能带结构,为二维声子晶体新型声屏障的设计提供理论依据和方案,以此降低轨道交通噪声对沿线声环境的影响。

1 声子晶体原胞模型

高速列车的噪声源主要包括轮轨噪声、气动噪声和集电噪声等。既有研究成果指出轮轨噪声始终是占主导地位,300～2 500 Hz钢轨的声辐射最为重要,在更高频率时,轮对就成为了最重要的辐射源[20]。牵引系统噪声对转向架区噪声的贡献频段主要为中高频段,占据主导作用[21]。因此,如果要进一步控制列车通过噪声,就必须控制轮轨噪声。我国普通高速列车以270～340 km/h的速度运行时,车外噪声峰值频段主要集中在1 600-2 000 Hz,测试结果表明轮轨噪声在630～4 500 Hz频段内的噪声分量始终占主导地位[22]。因此本文在分析时主要依据轮轨噪声的频段范围选取1～4 500 Hz范围的声激励。

基于Bragg带隙理论建立二维声子晶体结构理论分析模型,其中排布方式采用正方形晶格,散射体采用空心钢管材料,周期排布于空气基体。由于钢材质的声阻抗远大于空气声阻抗,因此,当声波从空气基体传至钢管散射体时,则会在界面上发生全反射现象,钢管内的空气无法响应外界波动,导致声波无法在钢管空心内传播。由于散射体壁厚对第一带隙起始频率、截止频率以及带隙宽度的影响并不明显[23],本文在研究各类参数对声子晶体带隙影响时简化了壁厚。此外选择钢管作为散射体时,为节省材料可尽可能采用壁厚较薄的钢管。

采用有限元方法求解二维声子晶体的离散关系,将一个原胞划分为有限个网格单元后,研究的问题则转化为一般的特征值问题。

主要根据文献[11]中公式得到对于一个二维声子晶体晶胞特征方程的离散形式可表示

(K-ω2M)U=0

(1)

式中:U=[U1,U2,…,UN]T为节点位移矩阵,Ui=[ui,…,vi]T;K和M分别为单元刚度矩阵和质量矩阵。

根据周期系统Bloch定理,结构的位移场可表示为

u(r)=uk(r)e(ikr)

(2)

式中:uk(r)为晶胞中具有相同周期边界条件的矢量函数;k=(kx,ky)为波矢量,取值限制在第一Brillouin区内;r=(x,y)为节点坐标矢。

假如单个晶胞在边界上能够满足Bloch周期边界条件,则整个周期结构均满足该边界条件。将式(2)沿着周期方向施加于单个晶胞边界上,可得周期边界条件为

U(r+a)=U(r)e(ika)

(3)

式中,a为晶格常数。

联立边界条件式(1)和式(3),利用COMSOL多物理场耦合有限元分析软件可直接求解式(2)的特征频率,即能得到相应的能带结构特性曲线。

假如Bragg散射型声子晶体的基体为气体,则基体中的弹性波仅表现为纵波形式,因此带隙源于相邻元胞间反射波的同向叠加,其带隙中心频率一般可根据式(4)求得。

(4)

式中:f为带隙中心频率;c为基体声速;a为晶格常数。根据轮轨噪声的峰值频带特性,选取1 500 Hz为第一带隙的目标频率,可求得晶格常数a=11.5 cm,为了便于计算,在求解时晶格常数a取为12 cm。声子晶体基础结构设计的原胞和第一Brillouin区,如图1所示。三种改进后声子晶体原胞模型示意图,如图2所示。

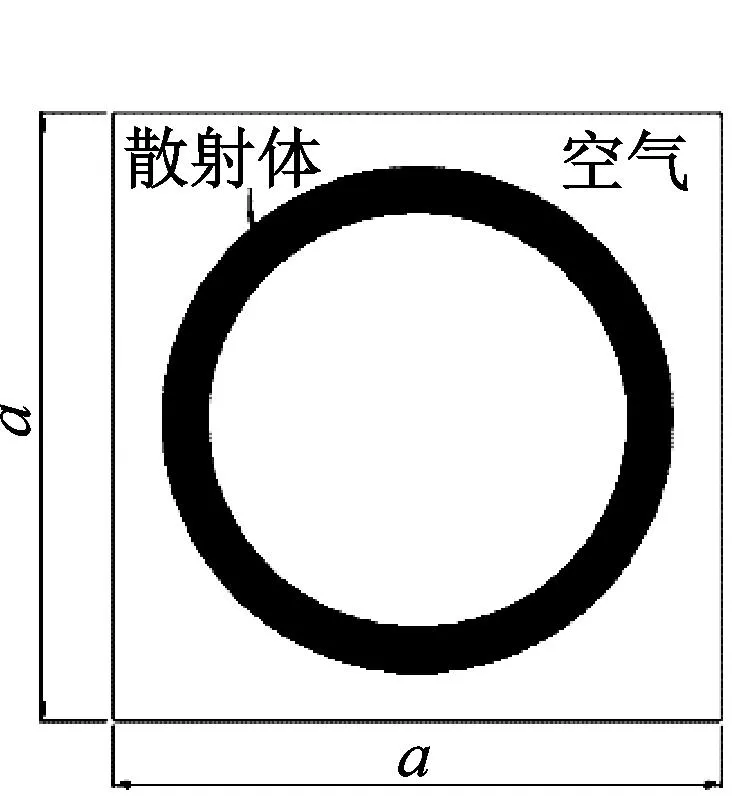
(a) 单空心原包

(a) 四复合十字型原胞

有限元模型中长方形波导的上、下边界均采用周期性边界中的连续性边界,达到模拟波导y方向无限长度理想条件,可得到声子晶体型声屏障最佳的噪声控制效果。空气域外层均设置为完美匹配层(perfect matched layer, PML),当适当调谐时,该层吸收频域问题内所有的输出波能量,并且没有其他阻抗失配导致的边界处的伪反射,以此避免平面波反射引起的干扰,且在PML中网格设置5层最大波长的一半厚度,剖分的网格大小与计算区域网格大小相当,这样可以提高网格质量和收敛性。声压激励则利用Comsol软件的背景压力场进行设置,入射波选择幅值为1 Pa的垂直入射平面波,以此计算声压在五周期散射体排列波导模型中的传递损失,其中传递损失可表示为

(5)

式中:Pin为入射波声压;Pout为透射波声压。

2 声子晶体设计模型的带隙特性

利用Comsol软件计算不同声子晶体原胞的带隙特性和声传输特性曲线,由于带隙特性主要基于理想声子晶体,结构的Floquet边界设置如式(6)所示

ui(x+a,y+a)=ui(x,y)e-i(kxa+kya)

(6)

波矢k沿着第一布里渊区的高对称方向(ΓX-XM-MΓ)进行扫描(见图1(b)),即可得到能带图,如图4～7所示。声子晶体声屏障原胞模型的材料属性如表1所示。

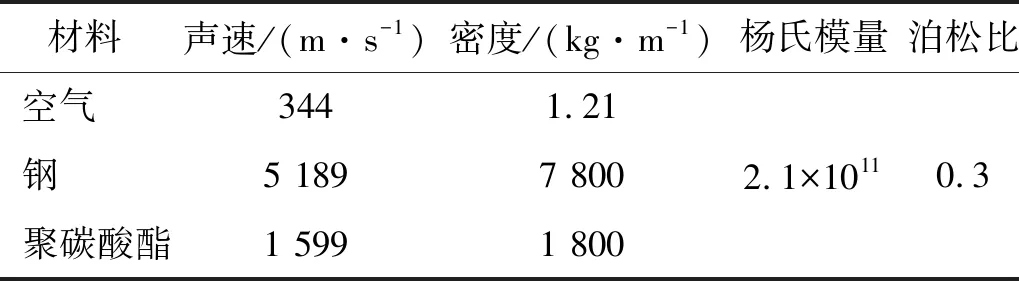
表1 声子晶体声屏障原胞模型材料属性

图5 四复合十字型原胞能带图与传输特性曲线对比

图6 四复合夹隔板原胞能带图传输特性曲线对比

图7 开口内嵌四复合型原胞能带图传输特性曲线对比

各类声子晶体原胞钢管的半径外径、壁厚等尺寸如表2所示。

表2 各个形式声子晶体原胞尺寸

单空心原胞结构存在三条完全带隙,与传递损失的衰减域吻合较好,参见图中深灰色矩形,分别为62～135 Hz、888～1902 Hz和1 904～2 360 Hz。由此可知,弹性波在上述频段内传播时得到了有效抑制,声波无法在该结构内的任何方向传播,其中第二条完全带隙的频宽最宽,频率跨度为1 014 Hz。完全带隙的产生主要是因为周期变化的结构与弹性波发生相互耦合作用,与散射体的反射波反向叠加,从而形成声波的干涉作用导致声波相消。

四复合十字型原胞模型采用四根空心钢管相切排列,该结构形成了四条完全带隙,分别为120～128 Hz、783～2 105 Hz、2 371～3 191 Hz和3 844～4 171 Hz;带宽分别为8 Hz、1 322 Hz、820 Hz及327 Hz。由于单个原胞内散射体数量的增加,加强了散射体间的反射作用,从而引起带隙起止频率和终止频率的升高,同时产生了多条ΓΧ方向带隙和ΧΜ方向带隙,导致声波在该方向上无法传播,在上述两种带隙内也能起到一定的隔声作用。

四复合型夹隔板原胞模型采用四根空心钢管与四块长度5 cm和厚度1 cm的聚碳酸酯隔板相切排列,高度与单空心钢管保持一致,该结构形成了三条完全带隙,分别为102～163 Hz,2 426～2 831 Hz和3 411～4 611 Hz,带宽分别为61 Hz、405 Hz及1 200 Hz。由于增加了聚碳酸酯隔板,增加了原胞内的填充率,并且起止频率、截止频率以及带宽都有所增加。

开口内嵌四复合型原胞模型采用在一根空心开口钢管内排布四根空心钢管的形式,空心开口钢管的开口角度为30°方向朝向背景压力场,内部空心钢管的半径和壁厚分别为1.9 cm和0.2 cm。该结构存在七条完全带隙,分别出现在457～622 Hz、1 025～1 119 Hz、1 123～1 318 Hz、1 463～1 886 Hz、2 010～2 360 Hz、2 949～3 184 Hz以及3 937～4 410 Hz,带宽分别为165 Hz,94 Hz、195 Hz,315 Hz,423 Hz,350 Hz和473 Hz。由此可知,这种排布方式设计的声子晶体原胞结构形成的带隙最多,其原因在于首先对散射体进行开口处理,使得钢管内部形成了Helmholtz共振吸声腔:声波从散射体开口进入钢管内部,与开口处的空气和内部空间产生共振,使部分声能转换成热能,从而消耗声能;其次在内部嵌入四根相切空心钢管,加剧了声波在吸声腔内与散射体间的Bragg反射,进而增强了干涉效应的频次,导致声波的传递较为复杂,出现了多条频带较窄的完全带隙。

3 关键参数对声子晶体带隙特性的影响

完全带隙的产生基于Bragg散射原理,散射体各项关键参数对完全带隙的形成有着至关重要的影响,因此本文进一步详细研究了不同声子晶体设计模型的散射体半径、隔板几何参数、开口角度和内部钢管填充率等关键参数对其带隙形成的影响。根据文献[13]可知,散射体壁厚对起始频率、截止频率以及带隙宽度影响并不明显,故本文忽略了散射体壁厚的影响。在此需要强调,由于散射体在其内部可形成低频共振,故空心散射体较之实心散射体能够增加一条低频完全带隙。

3.1 散射体半径对带隙特性的影响

针对散射体半径对带隙特性的影响,本文主要以单空心原胞声子晶体、四复合十字型原胞声子晶体和开口型原胞声子晶体为研究对象,其中晶格常数a为12 cm,壁厚t为0.5 cm保持不变,不同散射体半径对带隙的影响规律,如图8所示。

(a) 单空心原胞声子晶体散射体半径对带隙的影响

由于,散射体半径对单空心原胞声子晶体第一完全带隙的影响很小,因此主要分析散射体半径对第二完全带隙的影响。由图8(a)可知,单空心原胞声子晶体散射体半径小于3.7 cm,钢管包括内部空心在整个晶胞中所占的面积之比即原胞中散射体的填充率F不足30%时,将不会形成完全带隙;当随着散射体半径的不断增大至4.7 cm,即填充率大于50%时,第二完全带隙才能达到理想带宽。例如,当散射体半径由4 cm增大至5.75 cm时,相应的起始频率由1 655 Hz降至941 Hz,截止频率则从1 737 Hz升至到2 295 Hz,由此表明随着填充率的不断增大,进而增大了带隙宽度,因此填充率对单空心声子晶体的带隙宽度有着重要影响;由图8(b)可知,散射体半径对四复合十字型原胞声子晶体的带隙影响规律与单空心原胞声子晶体类似。由此表明散射体半径主要通过影响声子晶体的填充率,对带隙宽度起着重要作用。填充率可表示为

(7)

式中:R为钢管外径;a为晶格常数。

3.2 四复合夹隔板型声子晶体隔板几何尺寸对带隙特性的影响

晶格常数a=12 cm、散射体半径r=2.5 cm以及壁厚t=0.5 cm保持不变,分别研究四复合夹隔板声子晶体中隔板长度和厚度对其带隙特性的影响,如图9所示。

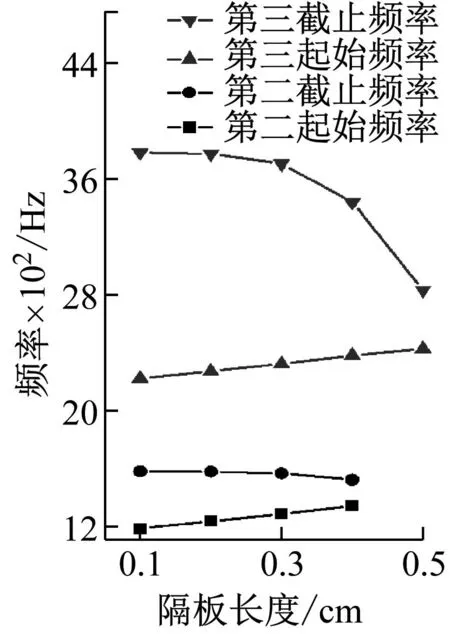
图9 隔板几何因素对带隙的影响

隔板几何尺寸对四复合夹隔板声子晶体原胞第一带隙的影响很小,因此仅讨论对第二和第三完全带隙的影响。由图9可知,四复合夹隔板声子晶体的带宽随隔板长度的增加而减小;随隔板厚度的增加,带宽则有所增大。因此隔板的长度和厚度也是该设计中影响带隙的关键参数。由此表明在实际的工程应用中,开展该声子晶体设计时,尽可能选择长度较短且较厚的隔板。

3.3 开口角度及内嵌钢管半径对带隙特性的影响

开口钢管的半径和壁厚分别取为5.5 cm和0.5 cm,分析外部钢管开口角度的影响时,内部钢管半径和壁厚分别设定为1.9 cm和0.2 cm保持不变;探究内部钢管半径的影响时,外部钢管开口角度设定为30°方向朝向背景压力场。研究结果如图10所示。

(a) 开口角度/(°)

由图10可知,外部钢管开口角度和内部钢管半径分别影响该声子晶体结构的第四、第六以及第七带隙。

随着外部钢管开口角度的不断增大,带宽呈减小的趋势,并且完全带隙则会出现整体向更高频率偏移的现象。内嵌钢管半径对不同带隙的影响差别较大,第六带隙的起始频率随着半径增大向上偏移,而第七带隙的截止频率向下偏移,两条带宽均有减小的趋势。开口内嵌四复合型声子晶体的开口角度和内嵌钢管半径对带宽影响并不明显,但是对整体带隙影响较为复杂,不同的开口角度和钢管半径有时会在不同频段产生不同数量和宽度的带隙。因此,在实际工程应用当中应选择相对较优的开口角度和半径。

4 排列周期与散射体半径对隔声性能的影响

建立各类声子晶体声传输特性曲线模型,见图3。声激励为垂直入射的平面波,不同排列周期时声子晶体几何参数均与表2相同。单空心声子晶体的声传递损失曲线,如图11所示。

(a) 不同排列周期

由图11可知,单空心声子晶体在带隙范围内均具有良好的降噪效果,且与该声子晶体的带隙范围基本吻合。声子晶体的隔声性能随排列周期数的增加而提升,原因在于声子晶体作为周期结构,其周期数在弹性波的抑制方面起着重要的作用(见图11(a))。因此在声屏障领域的实际工程应用中可考虑实际安装情况等,尽可能提高周期排列数目。

由图11(b)可知,不同散射体半径对该声子晶体结构的声传递损失频谱曲线,即不同填充率对声传递损失的影响,第一完全带隙的损失域频率范围随填充率的增大而变宽,该现象也印证了第三节分析中声子晶体散射体半径对带隙特性影响的规律。单空心管声子晶体的主衰减域(600～2 400 Hz)能很好地覆盖高速列车运行时轮轨噪声的峰值区域,并且该声子晶体结构具有易生产、施工便捷、衰减域较为理想等优点,在声屏障领域的应用适用于工况简单,噪声源变化小且稳定的大多数路段。

一般情况下声子晶体周期数越多,可近似认为更加接近理想模型(无限周期),能过提升隔声效果。为了进一步分析声波在声子晶体中的传播规律,四周期和五周期单空心管声子晶体在1 451 Hz的声传递损失声压云图如图12所示。在该声子晶体结构的完全带隙频段,声波很难进行有效传播,并且五周期排列方式在声传递损失方面优于四周期排列的声子晶体结构。

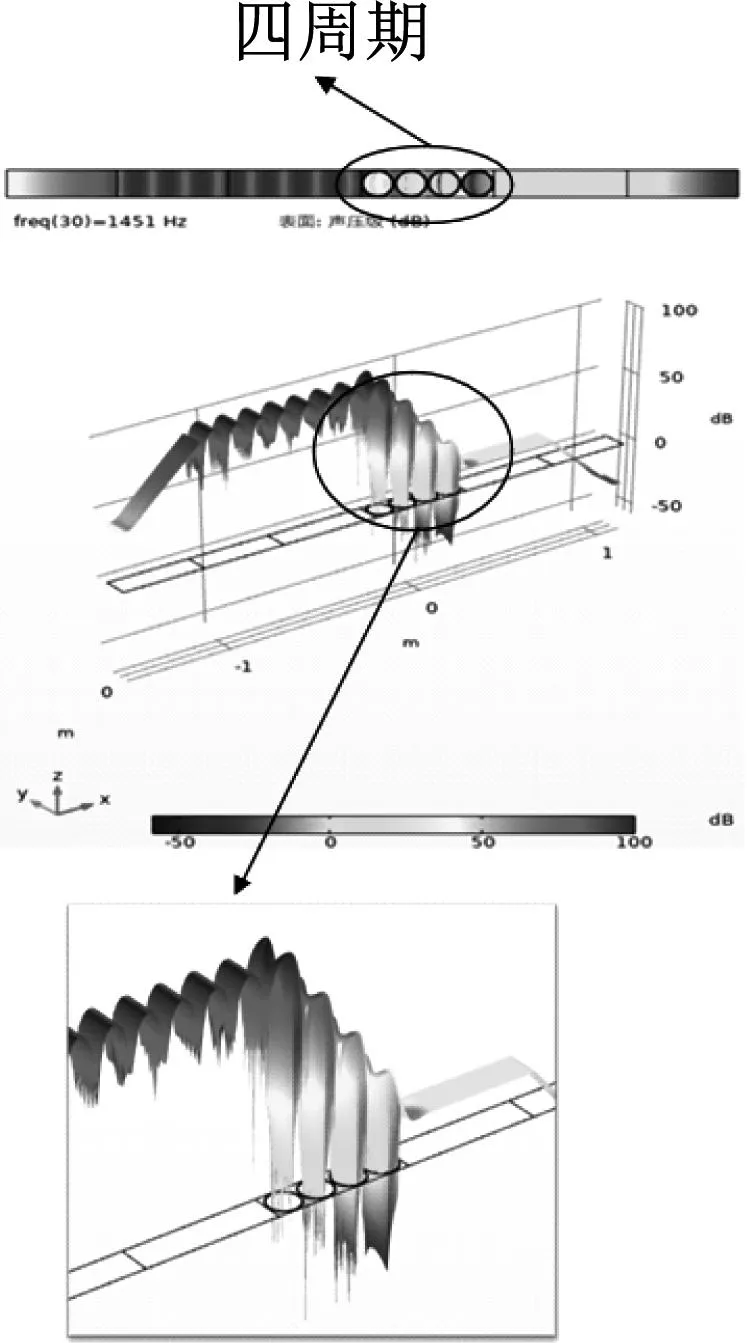
(a) 四周期

四复合十字型声子晶体结构的声传递损失频谱曲线可得到与单空心管声子晶体结构相似的声传递损失规律,表明周期数可增强隔声性能,散射体半径不仅增强了该结构的隔声性能,同时扩展了隔声带宽,如图13所示。在3 300～3 800 Hz也出现了一段较好的抑制范围,主要是因为ГX方向带隙对该方向上的声波产生了抑制作用;方向带隙虽然能够抑制弹性波的传播,但仅在特定方向上。由此可知,如将声子晶体结构设计应用于实际声屏障的工程领域,最佳设计方式应尽可能设计出多条完全带隙,形成隔声效果更优的衰减域,可适用于噪声源复杂的不稳定路段。

(a) 不同排列周期

5 其他相关参数对隔声性能的影响

对于四复合型夹隔板声子晶体和开口内嵌四复合型声子晶体两种结构其不同排列周期与不同散射体半径即填充率F对隔声性能的影响与前两种结构所产生的结果基本保持了相同的规律。因此,本章将对其隔板几何尺寸、内嵌钢管半径、外套钢管开口角度等相关参数进行分析。

四复合型夹隔板声子晶体结构的声传递损失频谱曲线,如图14(a)所示。由图14(a)可知,隔板长度和厚度对声传递损失的影响较为复杂,但总体上与带隙的变化规律基本吻合。其中当隔板长度小于5 cm时,隔声曲线在3 500～4 500 Hz的主要隔声频段则会发生偏移,其原因在于隔板长度对反射波的影响更大;隔板厚度主要影响在该频段的总体隔声量,厚度减小隔声性能也有所减弱。由此可知,如在声屏障设计中采用四复合型隔板声子晶体结构,对于隔板的参数选择,长度可完全根据抑制噪声类型的频率范围设计其带隙特性;而厚度越大,在隔声量以及频率范围均会产生影响,应根据实际工程应用情况最终确定。

(a) 四复合型夹隔板声子晶体传输特性曲线

开口管内嵌四复合型声子晶体结构的声传递损失频谱曲线,如图14(b)所示。由图14(b)可知,该设计在较低频段(小于2 500 Hz)内对声波的抑制作用明显优于其它三种设计方案。由于该结构可形成Helmholtz共振吸声腔,增大了共振时振子空气质量,因此该结构可形成低频带隙;在2 500～3 500 Hz,该结构对声波的抑制作用并不理想,由于此时仅存在MГ方向带隙,但声波的传播只在激励源一侧产生,并且在ГX方向带隙上的声传递损失性能优于MГ方向带隙,导致声波能够完全穿过声子晶体结构。此外由于开口的存在,声波在MГ方向传播时晶胞的周期性抑制作用减弱[24]。

四种声子晶体结构设计在不同频率下的声传递损失云图,如图15所示。由图15可知,声波在完全带隙中传播时受到明显的抑制,而在无带隙的频率范围,声波的传播规律十分复杂,但通过声子晶体结构的透射声波与入射声波的特性相近,声子晶体结构的隔声作用较弱。因此基于声子晶体设计轨道交通声屏障时,为了提升声屏障的隔声性能,最佳设计可根据实际的环境要求、轨道交通噪声源的比重及其声辐射特性,进而选择更加具有针对性的声子晶体型声屏障。