刚性弹体冲击金属网网孔的试验和数值分析

2023-12-18黄祺临崔廉明

振动与冲击 2023年23期

汪敏, 黄祺临, 周帅, 崔廉明

(1.陆军勤务学院军事设施系,重庆 401311;2.军事地下建筑工程军队重点实验室,重庆 401311)

在维和行动中,近距离作战或城市巷战是常态形式,因此,近程武器如火箭弹、迫击炮弹等日益成为维和部队军事设施的主要威胁[1]。金属网相比实体结构,具有重量轻、通透性好、力学性能优异等特点,随着编网用钢丝强度、韧性的提高,利用高强高韧性钢丝(强度大于1 770 MPa、弯折或扭转次数均大于20次)编织而成的金属网在军事设施、工事掩体的防护屏障方面得到了应用,主要目的是用于拦截近程武器的打击,降低军事设施遭受近程武器直接命中而引起的人员生命和财产损失[2～3]。利用金属网对弹体进行拦截,其拦截原理为:弹体冲击金属网时承受的过载力造成引信提前作用,战斗部提前起爆[4]。图1为金属网对火箭弹进行诱爆拦截现场试验。从图1可以看出,弹体撞击金属网的瞬间战斗部起爆,金属网成功对弹体进行了诱爆拦截[5]。利用金属网对弹体进行诱爆拦截,搞清楚金属网在弹体冲击作用下的力学性能是一个基础性的工作,这对于合理设计和优化金属网尺寸结构、提高金属网对弹体的拦截可靠性和拦截效率等方面都具有很好的指导意义。

图1 金属网对火箭弹的诱爆拦截试验

目前关于高强钢丝编织的金属网在冲击荷载作用下的力学性能研究主要集中在地质灾害防治领域和工程冲击爆炸防护领域。在地质灾害防治领域,主要研究金属网在崩塌落石冲击作用下的力学特性,如Cazzan等[6]开展了落石冲击金属网的数值分析,考虑了落石直径和冲击速度(20～110 m/s)对金属网防护效果的影响;Spadari等[7]采用数值方法研究了金属网在小尺寸落石中低速冲击下的“子弹效应”和破坏特点;Buzzi等[8]分析了金属网的网格尺寸、落石尺寸和落石速度等对金属网拦截效果的影响;Boetticher等[9]开展了金属网平面内拉伸试验、落石冲击金属网的试验,基于试验研究结果建立了金属网在落石冲击作用下的数值计算模型;郭立平等[10]提出了一种基于力流等效的环形网顶破力学行为的解析方法,该方法可以揭示网片承载的薄弱区分布特征,反映网片顶破极限状态下径向环链受拉特征;金云涛等[11]提出了一种正交钢丝环链网片顶压力学行为薄膜等效计算方法,推导了等效薄膜的应力-应变关系;齐欣等[12]开展了柔性环形网顶破受力归一化分析,提出了环形网片拉伸变形的解析计算方法。在工程冲击爆炸领域,孙波等[13]采用数值分析方法研究了金属网降低爆炸飞石的冲击速度,限制其飞散距离等问题;Xiao等[14]开展了利用金属网耗散爆炸冲击波的实爆试验和数值分析,研究了金属网对爆炸冲击波耗散的效果;Wang等[15]开展了飓风卷起的飞石撞击金属网的试验和数值分析,研究了飞石速度(20～150 m/s)和冲击能量等的影响。

由于弹体外形的特点,当采用金属网拦截时,弹体往往作用于金属网的网孔位置(如图2所示),而从目前的研究成果看,均是考虑较大岩体冲击金属网的局部区域,而考虑冲击作用于金属网网孔部位的相关试验和数值模拟研究还少见报道。基于以上原因,为研究金属网网孔在刚性弹体冲击作用下的力学性能,依据图1实弹拦截试验现象,设计并开展了刚性弹体低速冲击金属网网孔的试验,在此基础上,结合高强钢丝在中低速应变率下的材料性能测试结果,采用LS-DYNA软件建立了刚性弹体冲击金属网网孔的数值模型,分析了弹体口径、弹体质量、弹体冲击速度对弹体和金属网相互作用的影响。

1 刚性弹体低速冲击金属网网孔的试验

1.1 刚性弹体装置和金属网的设计

由于火箭弹、迫击炮弹等近程武器种类繁多,形状各异,根据典型近程武器的外形[16],设计了口径为D=82 mm刚性弹体装置。弹体装置前半部分按弹头外形制作,后半部分为弹头配重部分,用以控制弹体装置自由下落的姿态,增大瞬时冲击能量,保证金属网网孔被弹头配重部分冲击破坏。刚性弹体装置的设计及具体尺寸如图3所示。

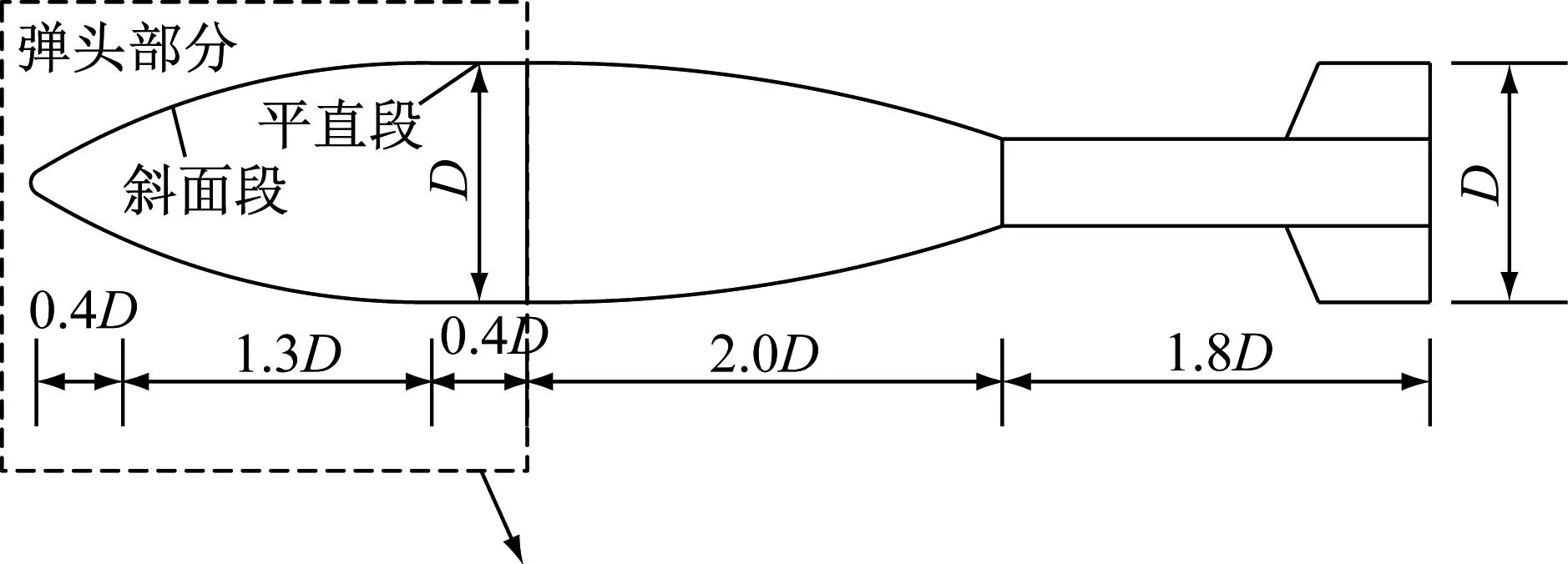
图3 刚性弹体装置布置及尺寸示意图(mm)

根据弹体口径和外形特点、实弹拦截试验效果,设计的金属网规格尺寸,如图4所示,金属网宏观尺寸近似为正方形。图4中d为编网钢丝直径;沿水平方向,菱形网孔短边尺寸为x(+/-3%);沿竖直方向,菱形网孔长边尺寸y(+/-3%);菱形网孔锐角为β(+/-2°);网孔内切圆直径为Di;沿垂直面内方向,外边界厚度htot;内净厚度hi。具体参数如表1所示。

表1 金属网规格尺寸参数

图4 金属网规格尺寸图

1.2 冲击试验平台及方案设计

设计的金属网冲击试验平台如图5(a)所示,宏观尺寸为2 m×2 m×1.5 m,其中主要部件为金属网悬挂与张拉装置,见图5(b)所示。

(a) 冲击试验平台

金属网悬挂与张拉装置分为两部分,一部分为连接金属网的U型连接件,另一部分为可移动连接系统。U型连接件可以固定金属网的四个边界,约束金属网平面内的自由度;可移动连接系统可以对金属网进行张拉,单侧单向可张拉约0.01 m,这样可以保证每次试验前,金属网均处于预张紧状态。试验平台可开展1 m×1 m金属网的冲击试验。

金属网与弹体装置安装后照片如图6所示。刚性弹体装置采用304不锈钢制作,总重量约为18.92 kg,通过挂钩与自动脱钩装置相连,而后脱钩装置与行车相连。试验时,将刚性弹体装置对准金属网中间位置网孔后,尽量保证弹体纵向与金属网平面呈α=90°,之后采用行车将弹体装置吊起到一定高度,通过远程操控脱钩装置对弹体装置进行释放。

图6 金属网与刚性弹体装置安装照片

弹体装置在自由下落的过程中,得到冲击速度和初始动能,每次刚性弹体冲击装置的起吊高度均一致,按下式计算刚性弹体装置的速度和动能

(1)

E=mg(h2-h1)=2.058

(2)

式中:h2为刚性弹体装置起吊高度,h2=14.5 m;h1为金属网距地面的高度,h1=1.4 m;v为刚性弹体装置的冲击速度,m/s;E为动能,kJ;m为刚性弹体装置质量,kg;g为重力加速度,取g=9.8 m/s2。

共开展了三次金属网网孔受弹体装置冲击的试验,利用高速摄像机观测刚性弹体装置冲击金属网网孔的动态过程,并利用后处理软件获得弹体装置接触金属网网孔时的偏转角度和冲击过程中的速度变化关系曲线。考虑到弹体装置总长约为392.2 mm,为充分捕捉弹体装置冲击金属网网孔的动态过程,在拍摄过程中,高速摄像机设置的采样频率为2 000帧/s。

1.3 冲击试验结果分析

弹体装置冲击金属网网孔的试验中,弹体装置对准金属网中间网孔的中心位置,采用脱钩装置对弹体装置进行释放,自由下落。由于在释放的瞬时,弹体装置很难保证垂直下落而不发生偏转,因此,每次弹体装置自由下落冲击金属网网孔接触的瞬时,其与金属网平面的夹角α均不相同(图6)。为研究的方便,选取了三次金属网网孔受弹体装置冲击试验工况中,偏转角度最小的一组工况进行研究,选取的工况如下:

弹体接触金属网网孔的瞬时,α=91.72°,v=16.171 9 m/s。

对比理论计算的冲击速度和采用高速摄像机测试速度,两者较为接近,高速摄像机测试的速度较理论计算值偏大,最大偏差约为0.01%,说明了高速摄像和测试数据的可靠性。

图7中给出了金属网网孔受弹体装置冲击的动态过程照片,主要包括弹体装置接触金属网(图7(a))、弹头部分插入金属网网孔(图7(b))、弹体配重部分插入金属网网孔(图7(c))和金属网网孔破坏瞬间(图7(d))。分析图7可以看出,弹体装置与金属网网孔相互作用的冲击过程可以分为三个阶段。

图7 金属网网孔受弹体装置冲击动态过程

第Ⅰ阶段:弹头部分斜面段插入到金属网网孔中,弹头部分与金属网孔间发生相对位移,直至弹头部分斜面穿过金属网孔。这一阶段,金属网网孔卡住弹头部分,一起向下运动,同时弹头斜面段挤压金属网网孔,由于金属网为松散结构,网孔横向钢丝交叉节点位置存在接触滑移(见图8),网孔有一定的扩大,此时弹头部分与金属网孔间发生了相对位移,弹体装置在金属网网孔约束和相对滑移的联合作用下,冲击速度将缓慢下降,见图7(a)～7(b)所示。

图8 金属网网孔受弹体装置冲击破坏后照片

第Ⅱ阶段:弹头部分的平直段进入金属网网孔中,此时网孔对弹体装置的约束几乎无增大趋势,同时平直段与金属网网孔发生快速的相对位移,此时弹体装置的冲击速度衰减速率非常缓慢,弹体装置速度轻微下降,金属网网孔对弹体的反向作用力基本保持不变,见图7(b)～7(c)所示。

第Ⅲ阶段:弹体配重部分插入到金属网网孔中,弹体配重部分带动金属网继续向下运动,由于金属网网孔在弹体配重部分的挤压下继续扩大,对弹体的约束力也快速增大,此时弹体装置速度快速下降,直至金属网孔被弹体配重部分挤压破坏,见图7(c)～7(d)所示。

图8给出了金属网网孔受弹体装置低速冲击后的破坏照片。从图中可以看出,金属网破坏仅局限在单个网孔范围内,横向网孔交叉节点两侧有连接滑移,破坏的部位位于网孔横向钢丝交接节点位置,其余部分金属网网格基本恢复到初始状态。

2 刚性弹体冲击金属网的数值模拟及验证

2.1 材料参数

金属网网孔与弹体的相互作用属于动态过程,考虑近程武器(火箭弹、迫击炮弹等)在中低速(50～200 m/s)与金属网网孔撞击[17],金属网中高强钢丝材料一般在中低应变率变化范围内。因此,采用电子万能实验机和分离式霍普金森拉杆(SHTB)装置,开展了3 mm高强钢丝的准静态(应变率3.3×10-4s-1)和动态单轴拉伸(中低应变率200～3 000 s-1)力学特性研究。结合LS-DYNA软件中Cowper-Symonds Piecewize Linear Hardening材料的相关要求,采用塑性失效应变来考虑高强钢丝的破坏,按如下本构方程考虑高强钢丝应变率效应的影响[18]

(3)

根据准静态单轴拉伸试验,得到了高强钢丝塑性真应变和塑性真应力关系曲线,如图9所示。结合准静态和动态单轴拉伸试验测试结果,拟合得到了数值计算采用的高强钢丝材料参数如表2所示。

表2 本构方程采用参数

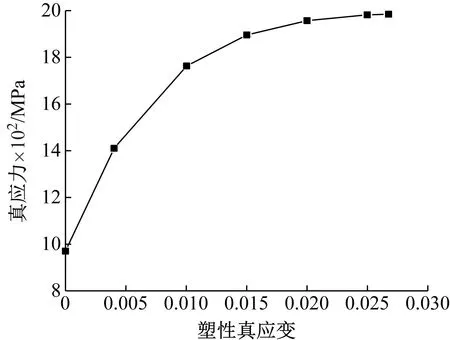
图9 高强钢丝准静态下塑性真应变与真应力关系曲线

相比金属网,弹体装置刚度较大,在冲击过程中未发生明显的变形,因此弹体采用等向线弹性材料模型MAT_RIGID,弹性模量为200 GPa,泊松比为0.3。

弹体装置的体积由弹头部分体积和弹头配重部分体积组成,根据试验弹体装置质量和体积,按式(4)计算弹体装置的密度ρdz

(4)

式中:mdz为刚性弹体装置的质量,mdz=18.92 kg;Vdz为弹体装置的体积,由弹头部分和弹头配重部分组成(图3),Vdz=2.578 m3。

按式(4)计算得到数值模型中弹体装置的密度,ρdz=7 339 kg/m3,保证数值模型与试验模型质量一致。

2.2 数值建模与计算方法

由于金属网在弹体装置冲击下,横向网孔的两个节点有较大的接触滑移,且一侧滑移节点发生了断裂破坏(图8),因此,为较好的模拟金属网网孔中钢丝这种松散的连接状态,需要精确的考虑节点位置钢丝的接触滑移、交叉节点位置钢丝弯折几何形状、复杂应力状态[19](钢丝弯折位置处于弯、剪、扭复杂受力状态)和断裂情况,除根据金属网制备工艺在建模过程中精确复现钢丝弯折部位的几何尺寸外,还需要细化此处的网格。此外,由于弹体装置与金属网网孔接触,因此,金属网中与弹体装置接触的网孔及周边网孔的钢丝网格也需要细化。

为兼顾计算效率和精度要求,在单元网格灵敏度分析的基础上,数值模型中钢丝弯折处单元过度角度定为10°,与弹体接触的金属网网孔直线段钢丝单元长度定为1 mm,其余部分金属网钢丝采用适当的粗网格。金属网和弹体装置的数值模型宏观尺寸尽量与实际尺寸保持一致,建立的刚性弹体装置冲击金属网网孔的数值模型如图10所示。

图10 刚性弹体装置冲击金属网网孔的数值模型

金属网中钢丝采用梁单元,截面类型采用Hughes-Liu-Beam算法,通过定义关键字DATABASE_EXTENT_BINARY,BEAMIP,输出梁单元的应力。梁截面为圆形,截面半径与钢丝实际截面尺寸一致。数值计算中,弹体装置与金属网中钢丝之间采用AUTOMATIC_NODES_TO_SURFACE定义接触,金属网中的钢丝与钢丝之间采用AUTOMATIC_GENERAL定义接触。

LS-DYAN中的接触滑动摩擦基于库仑公式并使用等效的弹塑性弹簧,计算公式如下[20]

μ=μd+(μs-μd)e-DC|vr|

(5)

式中:μ为摩擦因数;μs为静摩擦因数;μd为动摩擦因数;DC为衰减系数;vr为相对速度。

结合LS-DYNA的接触滑动设置,在数值计算中,设置弹体装置与金属网之间静摩擦和动摩擦因数分别为0.15,0.08,衰减系数为1.5;设置金属网间钢丝静摩擦和动摩擦因数分别为0.10,0.08,衰减系数为1.5。

考虑到冲击试验开始前,在安装金属网后对金属网四周进行预张拉,保证金属网处于预张紧状态。因此,为模拟整个试验过程,数值计算分两部进行计算:第一步对金属网四周水平向外侧进行张拉,每边张拉10 mm,尽量保持与试验安装中张拉尺寸基本一致,张拉后金属网保持该状态,之后设置金属网四周边界为固定约束状态(约束三个方向的平动自由度),此时弹体装置保持静止;第二步按试验观测条件,施加弹体初始冲击速度和初始倾斜角度,弹体自由落体冲击金属网网孔,数值计算中施加的重力加速度与式(2)一致。

2.3 数值计算与试验结果对比分析

为了验证数值计算结果的可靠性,将采用数值方法得到的金属网网孔受弹体装置冲击破坏瞬间的变形和等效应力云图,与试验中高速摄像拍摄的变形图和破坏后变形图进行对比,绘制在图11中。对比数值计算和试验得到的变形和破坏情况可以看出:金属网破坏瞬时,弹体冲击装置与金属网网孔相互作用的宏观变形情况基本一致,弹体装置冲击金属网孔破坏瞬时,仅受冲击的金属网网孔和周围局部网孔有较明显的变形,其余部分网孔变形不是很明显;金属网的破坏仅局限在受直接冲击的金属网网孔部分,破断点位于网孔横向交叉节点位置。

图11 弹体装置冲击金属网网孔的试验和数值模拟对比图

利用高速摄像机拍摄的弹体装置冲击金属网网孔动态过程,结合拍摄频率可以获得弹体装置从接触金属网网孔到金属网网孔发生破坏这段冲击过程中的速度变化曲线,同时提取了数值计算获得的弹体装置在相同冲击过程中的速度变化曲线,将两者进行对比绘制在图12中。从图12中可以看出:数值计算和试验测试获得的速度变化曲线趋势基本一致,均表现为明显的三阶段特征,这与弹体装置冲击的动态过程(图7)基本一致。为进一步对比数值计算结果的可靠性,提取第Ⅰ～Ⅲ阶段末时刻弹体装置从接触金属网到各阶段末时刻所经历的时间、弹体装置在该时刻的冲击速度进行对比,结果如表3所示。

表3 数值计算与试验测试的不同时刻时间和速度对比

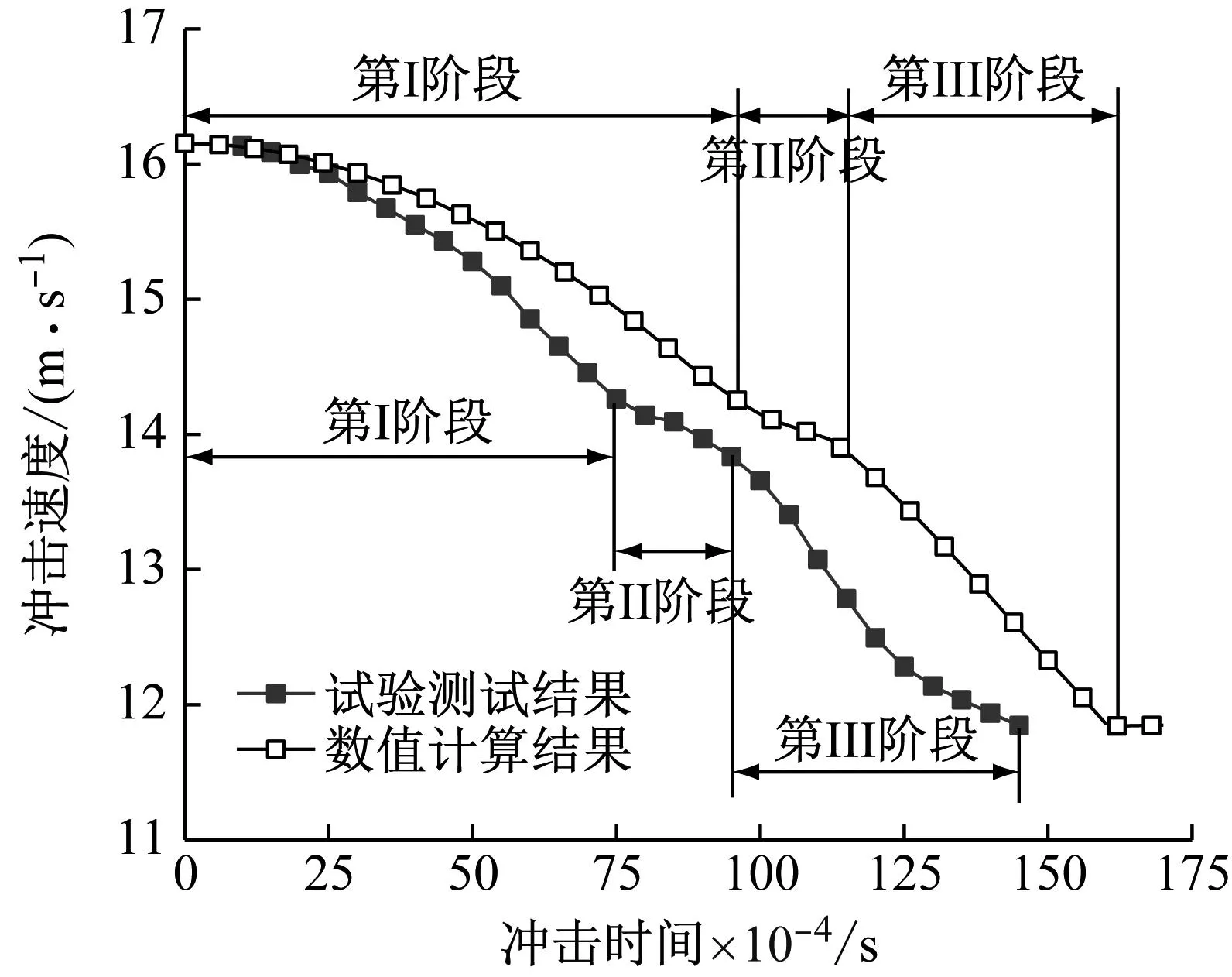
图12 弹体装置速度随冲击时间变化曲线

结合图12和表3,对比试验测试和数值计算获得的冲击过程经历时间,可以明显看出:在三个阶段末,数值计算得到的弹体装置所经历时间较试验测试结果明显滞后,最大偏差发生在第Ⅰ阶段,误差约28.0%,而后误差逐渐减小,到第Ⅲ阶段末,误差降为15.9%。出现这一现象的主要原因在于第Ⅰ阶段的相互作用时间(弹体装置从接触金属网到第Ⅰ阶段末所经历的时间),数值计算与试验测试结果的偏差较大,而第Ⅱ、Ⅲ阶段相互作用时间(第Ⅱ阶段末与第Ⅰ阶段末时间之差、第Ⅲ阶段末与第Ⅱ阶段末时间之差),数值计算结果分别为0.001 8 s、0.005 4 s,试验测试结果分别为0.002 s、0.005 s,两者非常接近。

对比弹体装置冲击金属网网孔时在三个阶段末时刻的速度可以看出,数值计算的结果与试验结果非常接近,误差在0.40%以内。

2.4 误差分析

从2.3节的对比分析可知,数值计算的速度变化曲线较试验测试获得的曲线在时间上有明显的滞后,特别是在第Ⅰ阶段非常明显,产生以上滞后的原因如下:

(1) 由于金属网为松散连接的三维空间结构,且在编织组装时允许有一些偏差,因此制备时很难精确的控制其铺开之后的尺寸,但数值计算中是严格的按照表1中相关参数建立的模型,没有考虑尺寸偏差,因此数值模型与实际的金属网在宏观尺寸、网孔尺寸上存在一定的区别,而以上区别易造成实际试验时金属网的张紧程度与数值模型的张紧程度不一致。从试验和数值计算的对比结果看,试验时金属网的面内实际张紧程度大于数值计算的张紧程度。

(2) 弹体装置在第Ⅰ阶段与金属网网孔相互作用时,弹体装置头部斜面段插入到网孔中,带动金属网一起向下运动,同时金属网网孔逐步扩大。金属网网孔的扩大速度直接影响第Ⅰ阶段的相互作用时间,而网孔扩大的速度又受弹体装置与金属网网孔间的动静态摩擦系数、弹体装置的冲击角度、金属网网孔的精确尺寸、金属网连接节点位置钢丝之间的相互滑移和静动态摩擦系数等影响。从试验和数值计算的对比结果看,数值计算中金属网网孔的扩大速度较试验要慢。

除第Ⅰ阶段相互作用的时间存在较大误差外,数值计算的第Ⅱ、Ⅲ阶段相互作用时间与试验测试结果吻合较好,且三个阶段末数值计算的速度与试验测试结果吻合也较好,这主要是由于在进入第Ⅱ阶段后,金属网内部连接节点位置均处于张紧状态且充分接触,后续金属网网孔的变形主要是弹体挤压而产生的拉伸变形,节点位置的滑移非常小,此时数值模型与试验时金属网网孔的状态基本一致,这一点在金属网网孔受弹体装置静压的试验中也观察到了[21],另外数值计算的金属网网孔破坏形态与试验获得的破坏形态非常一致也较好的验证了这一点。因此,第Ⅱ、Ⅲ阶段数值计算结果与试验测试结果基本吻合,误差很小。

总体而言,综合弹体装置的速度变化曲线、金属网变形和破坏情况的对比情况看,建立的金属网数值模型能够较好的考虑金属网中交叉连接节点位置的接触滑移和复杂应力状态,预测金属网在刚性弹体装置冲击作用下的变形和破坏情况。

3 刚性弹体冲击金属网网孔的参数分析及讨论

3.1 弹体口径、质量和冲击速度的影响

为进一步研究刚性弹体与金属网网孔的相互作用,基于高强钢丝在中低应变率下的材料本构方程和验证了的金属网网孔受刚性弹体冲击作用数值模型,采用数值分析方法对金属网网孔在刚性弹体中低速冲击作用下的力学特性开展参数分析,主要讨论弹体口径、弹体质量、弹体冲击速度的影响。

数值分析中,弹体口径设定为82 mm和107 mm,质量设定为3 kg、4 kg和5 kg,同时仅考虑弹头部位与金属网间的相互作用,去掉弹体装置的配重部分,通过改变弹体密度而达到预设质量。从图3中可以看出,弹头部分的外形与弹体口径相关。数值模型中弹体总长度Ldt(不考虑弹头配重部分)按式(6)计算

Ldt=1.3D+0.4D+0.4D

(6)

数值模型中弹体的相对密度,按式(7)计算

(7)

式中:mdt为预设数值模型中弹体质量;Vdt为弹头部分体积。

根据式(6)、(7)计算了两种口径、三种不同质量弹体数值模型的具体参数,如表4所示。

表4 数值模型中的弹体相关参数

数值分析中预设刚性弹体的初速度分别为50 m/s、100 m/s、150 m/s和200 m/s。为分析金属网网孔在刚性弹体冲击下的力学性能,重点考察了金属网网孔施加给弹体的峰值过载力Fmax和弹体穿过金属网损失的能量W,具体计算公式如下

Fmax=mdta

(8)

(9)

式中:mdt为预设数值模型中弹体质量;a为刚性弹体的峰值过载;v1为刚性弹体的初速度;v2为刚性弹体穿过金属网网孔的速度。

图13中给出了两类口径弹体(质量为5 kg)在速度为100 m/s时冲击金属网网孔的变形图。对于82 mm口径弹体,弹体冲击并穿过金属网网孔后,金属网网孔未发生破坏,其余速度冲击情况下变形情况也一致(图13(a)),而107 mm口径弹体冲击金属网网孔过程中,金属网网孔发生了破坏,破坏位置位于网孔横向交叉节点位置,其余速度冲击情况下变形情况也一致(见图13(b)所示)。

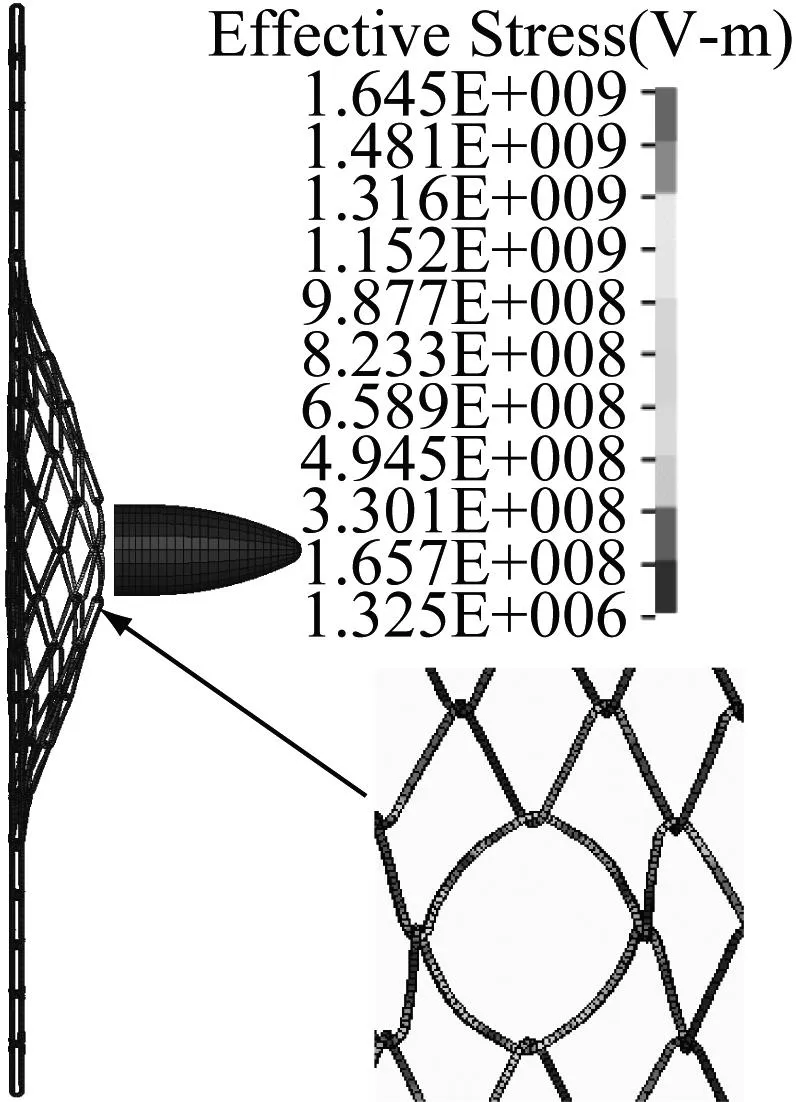
(a) 82 mm v=100 m/s

图14、15中选取了两类口径弹体(质量5 kg)在不同速度冲击金属网网孔,弹体达到峰值过载力时刻的变形和应力云图。从图14和15可以看出:

v=50 m/s

(1) 当冲击速度在50 m/s时,金属网整体上发生了漏斗型的拉伸变形,107 mm口径弹体冲击下金属网的整体变形较82 mm口径弹体更加明显;随着冲击速度的增大,金属网整体上的变形逐步减弱,金属网对弹体冲击变形的局部响应现象愈发明显,当冲击速度达到200 m/s时,金属网中仅存在与弹体接触的网孔以及与接触网孔节点相连的网孔发生变形,其余部位基本未发生明显的变形。

(2) 金属网中与弹体接触的网孔变形形态与冲击速度基本无关,均表现为接近刚性弹体剖面的变形,沿金属网网孔横向的两个节点发生较大的接触滑移,纵向两个节点未见明显的滑移。

(3) 在材料应变率硬化的影响下,随着冲击速度的逐渐增大,金属网中钢丝的有效应力峰值逐渐增大。

(4) 对比不同速度下,弹体与金属网网孔相对位置可以看出,虽然金属网的整体变形不一致,但当刚性弹体达到峰值过载力时,刚性弹体与金属网网孔的相对位置基本保持一致,因此,金属网网孔的变形形态也基本一致,即接近于此刻弹体剖面的变形。

表5、6中分别给出了两类口径刚性弹体在不同质量和不同速度下冲击金属网网孔时,刚性弹体受到的峰值过载力和穿过金属网网孔损失的能量。从表5和6可以看出:

表5 刚性弹体受到的峰值过载力

(1) 在相同的弹体口径和冲击速度作用下,随着弹体质量的增大,冲击动能逐渐增大,但弹体的峰值过载力和弹体穿过金属网损失的能量变化不明显,弹体质量对其受到的峰值过载力和能量损失影响很小;

(2) 在相同的弹体口径、相同的弹体质量情况下,随着弹体冲击速度的增大,弹体受到的峰值过载力逐渐增大,弹体穿过金属网损失的能量逐渐减小;在相同速度、相同质量情况下,弹体口径对峰值过载力和能量损失影响最大,107 mm口径弹体受到的峰值过载力较82 mm口径峰值过载力平均增大约2.3倍,穿过金属网损失的能量则是82 mm口径弹体的约2.3倍。

(3) 相比刚性弹体静压金属网网孔获得的弹体反向荷载,在弹体冲击作用下,82 mm口径弹体峰值过载力较静压试验增大约1.05～1.47;107 mm口径弹体峰值过载力较静压试验值增大约1.04～1.40。

3.2 金属网网孔与弹体相互作用规律的讨论

综合金属网网孔与弹体相互作用的试验和影响因素分析,金属网网孔与弹体相互作用有如下特点:

(1) 刚性弹体在冲击金属网网孔的过程中,由于金属网为松散连接的网状结构,网孔的四个节点均可在小范围内自由移动,特别是网孔横向两个节点钢丝的接触滑移更为明显,这主要是由于金属网的三维几何构造决定的,当金属网网孔受到弹体冲击时,横向两个节点处钢丝在复杂应力状态下首先发生破断。因此,在建立金属网数值模型时,需要精确的考虑金属网的三维编织状态、内部钢丝交叉节点位置的几何形态。

(2) 在冲击速度和弹体口径一致的情况下,弹体质量对峰值过载力影响不大。这主要是由于金属网为柔性结构,网孔也处于松散状态,当弹体撞击到金属网网孔时,由惯性作用导致的弹体过载力不大,随着弹体冲击的继续进行,金属网网孔随着弹体一起运动的同时,网孔受到弹体的挤压也逐渐形成接近弹体剖面的变形。金属网网孔最终的变形形态由弹体外形决定,应变率硬化效应由弹体冲击速度决定,虽然弹体质量增大,增大了金属网网孔受到的冲击动能,但弹体的峰值过载力仅与网孔最终的变形形态和网孔中钢丝的变形速率有关,因此,弹体口径和冲击速度是峰值过载力的关键影响因素。

(3) 对比不同口径弹体静压金属网网孔获得的反向荷载、弹体冲击金属网网孔获得的峰值过载力,在速度相同的情况下,不同口径弹体峰值过载力较静压试验值增大的幅度基本一致,这主要是由于钢丝的应变率硬化效应与弹体和金属网网孔间的作用速度相关,当速度一致的情况下,增加的幅度也基本保持一致。

(4) 金属网对弹体的能量衰减作用,与弹体的冲击速度反相关,这主要是由于弹体冲击速度较大时,金属网的整体变形越小,造成金属网整体吸收的能量减小导致;弹体质量对金属网衰减弹体冲击能量关系不大,这主要是由于弹体能量的衰减最终由金属网施加给弹体的过载力和作用距离决定,而这两点与弹体质量关联性不大;弹体口径对金属网的整体变形和金属网网孔的变形起决定因素,因此弹体口径越大,弹体穿过金属网网孔损失的能量也越大。