基于最不利塔顶位移相图法的风电塔筒动力屈曲研究

李万润, 范科友, 杜永峰

(1.兰州理工大学 防震减灾研究所,兰州 730050;2.兰州理工大学 甘肃省土木工程减震隔震国际科技合作基地,兰州 730050;3.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,兰州 730050)

传统化石能源带来温室气体的大量排放并导致全球气候的急剧变化,给人类社会带来了巨大的危害。因此,开发并利用绿色环保的能源就显得尤为重要。目前,以中、美两国为首的世界各国都在大力推进风能这种清洁能源,而截至2021年年底,全球累计风电装机容量就已达到837 GW,单2021年就新增装机93.6 GW,使得2021年成为风电行业有史以来第二好的一年[1]。另据国际能源署预计,到2026年,中国的陆上风电新增装机容量将比2015—2020年平均高出近25%,而海上总装机容量将增加两倍以上[2]。由此可知,我国风电的建设正以磅礴之势在不断向前推进。然而,风电塔筒作为一种“头重脚轻”的高耸薄壁结构,在外荷载作用下易发生屈曲破坏[3],并由此引发了一些风电事故,如图1所示。因此,把握风电塔筒的屈曲性能是至关重要的。

图1 风电结构的屈曲破坏[4-5]

目前,针对风电塔筒屈曲的设计主要还是基于静力条件下的工况,例如国际上较为通用的欧洲的IEC 61400-1(2005)[6]和德国的GL(2005)[7],都主要是基于静力条件下的屈曲设计,而我国作为一个地震频发的国家,地震动将是风电塔筒的控制荷载,基于静力的屈曲设计将不满足地震动作用下的工况。此外,考虑到风力发电机作为吸收风能的装置,当地震发生时,其有极大的概率是处于正常的运转工况下。因此,研究风-震耦合作用下风电塔筒的动力屈曲行为能够更好地为风电塔筒在屈曲方面的设计提供指导,有利于保障风电结构在我国的安全运营。

在对风电塔筒在风-震耦合作用下的动力性能进行研究之前,学者们大多还是将风和地震动分开考虑。首先是风电塔筒的抗风性能方面,Murtagh等[8]通过对风谱进行旋转采样分析运转工况下风电结构的风振响应问题。曾庆川等[9]基于改进的叶素动量理论研究了水平轴风电机组的气动性能。柯世堂等[10-12]则主要基于叶素动量理论,探讨了风电塔筒的疲劳损伤问题和风力发电塔轮系统的共振问题,并结合大涡模拟分析了不同停机位置下风电结构的风振响应。此外,潘方树等[13]则在计算停机工况下风电结构塔顶各方向最大荷载的基础上,对比分析了不同方法得到的临界屈曲荷载。黄国庆等[14]更是计算了风浪荷载作用下单桩海上风机的屈曲承载力,并基于此进行单桩海上风机的易损性分析。其次,在风电塔筒的抗震性能研究方面,Li等[15]指出长周期地震作用对风电塔筒的位移、加速度、应力和内力有重要影响。Xu等[16]则发现不同的初始缺陷程度将影响塑性铰在塔筒上出现的位置。而后,亦有学者对于风-震耦合作用下风电塔筒的动力响应进行了研究。主要有戴靠山等[17]对某在役风电塔筒进行了地震和风荷载下的失效概率的对比,并提出考虑风电塔筒特有设计使用年限的概率分析方法。席仁强等[18]则指出风电结构在地震作用下的响应与地震输入方向有关。Fan等[19]利用非线性有限元建立了与叶片耦合的风电结构的精确建模方法,研究了风和强近场地震的耦合作用下风电塔筒的倒塌模式。李万润等[20]在考虑叶片旋转效应的前提下分析了风电结构在风-震耦合作用下的动力响应,并探讨地震输入时刻对于该动力响应的影响。Yan等[21]更是研究了10 MW的单桩海上风电结构在风-浪-地震耦合作用下的动力响应问题,并指出风机所处环境的变化会导致风电塔筒屈曲模式的转变。

由此可知,虽然不少学者对于风电塔筒的抗风性能与抗震性能进行了研究,也发现塔筒易发生屈曲破坏这一现象,但是缺乏对于该屈曲现象的定量描述和细致探讨,亦鲜有针对风电塔筒在风-震耦合作用下的动力屈曲行为的全面揭示。因此,本文主要基于西北地区某2.5 MW风力发电机,在细致地考虑该风电结构所受风荷载的前提下,通过建立风电结构的有限元模型,分析不同输入角度对于风电塔筒在风、地震及风-震耦合作用下的动力响应的影响。最后,通过提出的“最不利塔顶位移相图法”来对风电塔筒在风-震耦合作用下的动力屈曲进行定量描述和细致探讨。

1 风荷载的生成

1.1 风场的生成

风可由脉动风和平均风叠加而成,即由一个静力过程叠加上零均值的高斯随机动荷载过程。对于平均风,本文采用Davenport提出的指数模型,即平均风沿高度的变化可表示为

(1)

式中:v和z为任一点的平均风速和高度;vs和zs为标准高度处的平均风速和高度,我国取10 m;α为地面粗糙度系数。

对于脉动风,本文采用Shinozuka等[22]提出的谐波叠加法来生成这一零均值的高斯过程。其中,第j个位置的随机过程fj(t)可表示为

(2)

式中:j为空间节点编号,j=1,2,3,4,5,…,n;N为脉动风频率分割份数;Δω=(ωu-ω0)/N,即频率增量,ωu和ω0分别为截断频率的上、下限;φml为独立、均匀分布在[0,2π]的随机数;文献[23]研究表明ωml=(l-1)·Δω+(m/j)·Δω时,可以增大模拟样本的周期;Hn×n(ω)为功率谱矩阵Sn×n(ω)的Cholesky分解,θn×n(ω)为Hn×n(ω)的幅角,其表达式如下

(3)

(4)

而在风的功率谱方面,本文按照我国规范采用了Davenport谱,其表达式如下

(5)

(6)

此外,空间上任意两点应具有相关性。因此本文采用文献[24]提出的任意空间两点的相干系数来修正式(3)以考虑空间上各节点之间的相关性。

1.2 风电结构风荷载的计算

本文对于风电结构风荷载的计算主要采用李万润等所提的方法,其可以很好地考虑叶轮的旋转效应及尾流的影响。在考虑计算成本和计算精度的条件下,本文通过选取具有代表性节点的风速以代表该节点所在一定区域内的风速,最后由风速生成风压,再由此生成该节点所在区域的等效集中风荷载时程曲线,而该等效集中风荷载即作用于选定的代表性节点上,如图2所示。将风电结构所受风荷载划分成三个区域:①塔筒非尾流影响区,主要通过伯努利方程来计算塔壁所受风荷载;②叶轮区,主要通过离散叶轮空间各点得到叶片上节点所受风速再结合叶素动量理论来计算叶片所受风荷载,进而得到整个叶轮所受的等效集中风荷载时程曲线;③塔筒尾流区,即通过选取基于高斯风亏的尾流模型来得到塔筒尾流区的风速,进而得到该区域内的风荷载时程曲线。

图2 风电结构风荷载区域划分及节点分布

本文以西北地区某137 m高的2.5 MW风力发电机为原型,其转速为12.1 r/min,取10 m处的平均风速为5.5 m/s,基于上述原理,得到了各区域的风速时程及其等效风荷载时程曲线,结果如图3～图6所示。图3与图4为叶轮区及塔筒非尾流影响区部分代表性节点的风速及其自功率谱,基于谐波叠加法可以很好地生成空间各点的风速,其自功率谱基本围绕在Davenport谱附近。而在考虑叶片的旋转效应后,发现叶片上节点所受风速时程比塔筒非尾流影响区的风速时程包含更多能量。由图5的等效叶轮风荷载时程曲线可知,其频谱相较塔筒非尾流影响区的风速将更以高频为主。因此,不考虑叶轮的旋转效应将弱化叶轮区的风荷载。尾流区各代表性节点所在区域的等效集中风荷载时程曲线(见图6)。由图6可知,随着高度的增加,尾流区塔壁所受风荷载将趋于0。

图3 叶轮区及塔筒非尾流影响区部分代表性节点的风速时程曲线

图4 叶轮区及塔筒非尾流影响区部分代表性节点的风速的自功率谱及Davenport谱

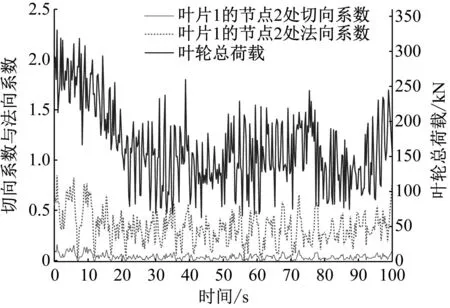
图5 叶片1的节点2处的切向系数与法向系数及等效的叶轮风荷载时程曲线

图6 塔筒尾流区各代表性节所在区域的等效集中风荷载时程曲线

2 风-震耦合作用下风电塔筒响应分析

有了前文的风荷载时程曲线,则可以将其导入ABAQUS软件中,并在建立风电结构有限元模型的基础上,通过隐式动力分析方法即可实现风电塔筒在风-震耦合作用下的响应分析。

2.1 风电结构的模型建立

本文主要以西北地区某钢制薄壁圆锥形的2.5 MW风力发电机为原型,通过S4R单元建立其有限元模型,并在各连接段设置了绑定约束[25]。此外,对于塔筒基底,本文则将其考虑为固结于地面。对于机舱与叶轮,本文则将其等效为了94 t与56 t的两个集中质量点,并与塔顶截面设置成刚体运动耦合,具体信息如图7和表1所示。而在塔筒材料参数方面,本文主要采用Q345D钢材及线性强化本构模型,其具体信息如表2所示。此外,考虑到屈曲时塔壁会有“折叠”的现象,本文又对该模型进行了“自接触设置”以保证结果的可靠性[26]。

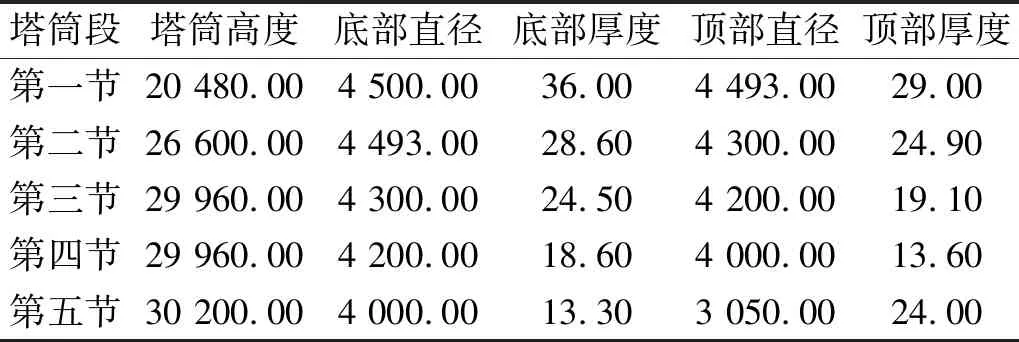
表1 塔筒尺寸信息

表2 塔筒模型的材料参数

2.2 模态分析

本文利用Lanczos法对该模型进行模态分析,提取了水平X向和Z向的前三阶弯曲模态及其对应的自振频率,前三阶弯曲模态如图8所示。对应的自振频率如表3所示。由此可知,水平X向和Z向的前三阶振型与其对应的自振频率十分接近。

表3 前三阶自振频率

X向一阶模态

2.3 不同输入角度对风电塔筒在风和地震动作用下的动力响应的影响

考虑到在风机的实际运转中,风可能来自任一方向,地震也可能来自任一方向,二者的组合将有无限种可能性,本文将水平方向上分为8个角度,以门洞朝向为0°,按照顺时针分别取45°、90°、135°、180°、225°、270°和315°,如图9所示。令风的输入角为α,地震动水平分量的输入角为β,在确定α后,再分别从其他8个方向输入地震动,通过这样的风-震耦合工况来考察风-震耦合作用下风电塔筒的最不利组合工况,进而分析风-震耦合作用下的风电塔筒动力屈曲性能,且为了更贴近真实的情况,本文输入的地震动均是按照地震动的两个互相垂直的水平地震动分量来输入的,这与地震动的单向输入相比会更贴近实际情况。

为与上述风-震耦合工况做对比及探讨输入角度对于风电塔筒在风和地震动作用下动力响应的影响,本文先考察了风电塔筒在地震动和风从不同角度输入下的动力响应。此外,考虑到塔顶、门洞和基底对于风电结构的敏感性(见图7),本文将利用塔顶位移和门洞与基底处的应力来阐述风电塔筒在风和地震动作用下的动力响应问题,并基于此确定风电塔筒的最不利组合工况。

2.3.1 地震动单独作用下风电塔筒的响应分布规律

本文从PEER数据库选取了三条经典地震动记录作为输入,分别是EI Centro波、Taft波和Kobe波。首先考察了在地震动单独从不同角度输入下引起风电结构塔顶位移在不同方向的最大响应分布及门洞与基底的最大Mises应力分布情况,如图10～图13所示。由于风电塔筒还处于弹性范围内,因而可以看到随着地震动输入角度的改变,塔顶在各方向上的位移响应规律也只是随着地震动输入角的改变而旋转了一个角度而已,其总体规律基本呈现出原点对称的特性,亦从反面说明了在弹性范围内,叶轮和机舱的质心相对塔筒中心的偏心对于塔顶位移响应的影响基本不大。而地震动从不同角度输入引起的门洞应力和基底应力的响应则表现出了一定的差异性,亦即应力对于外荷载作用方向的敏感性,且总体上来说地震动引起的基底应力要大于引起的门洞处的应力,这也揭示了在采取应力进行风电塔筒的抗震设计时要注意被考察位置及其与外荷载作用方向之间的影响。

图10 Kobe波单独作用下塔顶位移分布规律

图11 Taft波单独作用下塔顶位移分布规律

图12 EI Centro波单独作用下塔顶位移分布规律

图13 地震动单独作用下门洞应力及基底应力分布规律

2.3.2 风荷载单独作用下风电塔筒的响应分布规律

风荷载单独从不同角度输入所引起的风电塔筒塔顶位移在不同方向的最大响应分布及门洞与基底的最大Mises应力分布情况如图14～图15所示。由图14和15可知,风荷载单独作用引起的塔顶位移在不同方向上的响应也具有原点对称的特性,而风荷载从不同角度输入引起的门洞应力和基底应力大小不同且差异明显。此外,结合风荷载与地震动单独作用下风电结构的塔顶位移响应分布规律可知,风荷载对于塔顶的位移响应具有主导性。结合图13可知,风荷载对于塔筒门洞应力的影响相较地震动更具有主导性,而地震动对于基底应力的影响相较风荷载更具主导性。

图14 风单独作用下塔顶位移分布规律

图15 风单独作用下门洞应力及基底应力分布规律

但是从图14和图15可知,当风荷载从90°或270°输入时其所引起的门洞中点应力比之地震动从90°或270°输入时其所引起的门洞中点应力要小,在此种工况下的风对于基底处的应力影响与地震动对于基底处的应力影响水平相当。由此可知,风荷载和地震动的输入角度对于风电塔筒的动力响应具有很大的影响,而二者的耦合工况则更应进行深入探讨。

2.3.3 风-震耦合作用下风电塔筒的响应分布规律

本节基于前文对于风-震耦合工况的定义,分析了风-震耦合作用下风电塔筒的动力响应分布规律。需说明的是,在进行风-震耦合作用下风电塔筒的响应分析时,为消除瞬态响应的影响,本文的地震动都是在施加风荷载的20 s后再输入地震动。此外,叶轮平面始终考虑为与风向垂直,即风电结构有限元模型中的偏心质量会随着风向的输入而改变方向及位置。因此,本文的内容可为风电结构针对考虑不同地区主导风向而选择门洞朝向的问题上提供参考。

在确定某一风荷载输入角的前提下,地震从不同角度输入并引起风电塔筒塔顶位移的最大值,其总体规律基本呈现出原点对称的特性,如图16～图18所示。结合图14可知,在弹性范围内风电塔筒的塔顶位移主要由风荷载主导,风荷载或地震的输入角的改变对结果影响不大,塔顶位移最值基本接近。但是相较其他风-震耦合工况,当风荷载在270°输入、EI Centro波在180°输入以及风荷载在90°输入、EI Centro波在0°输入会导致塔顶位移相较其他工况下的塔顶位移要大许多,由此可知在考虑叶轮和机舱朝向的条件下,不能简单地将风荷载和地震荷载分开考虑,二者的耦合可能会诱发较大的几何非线性。

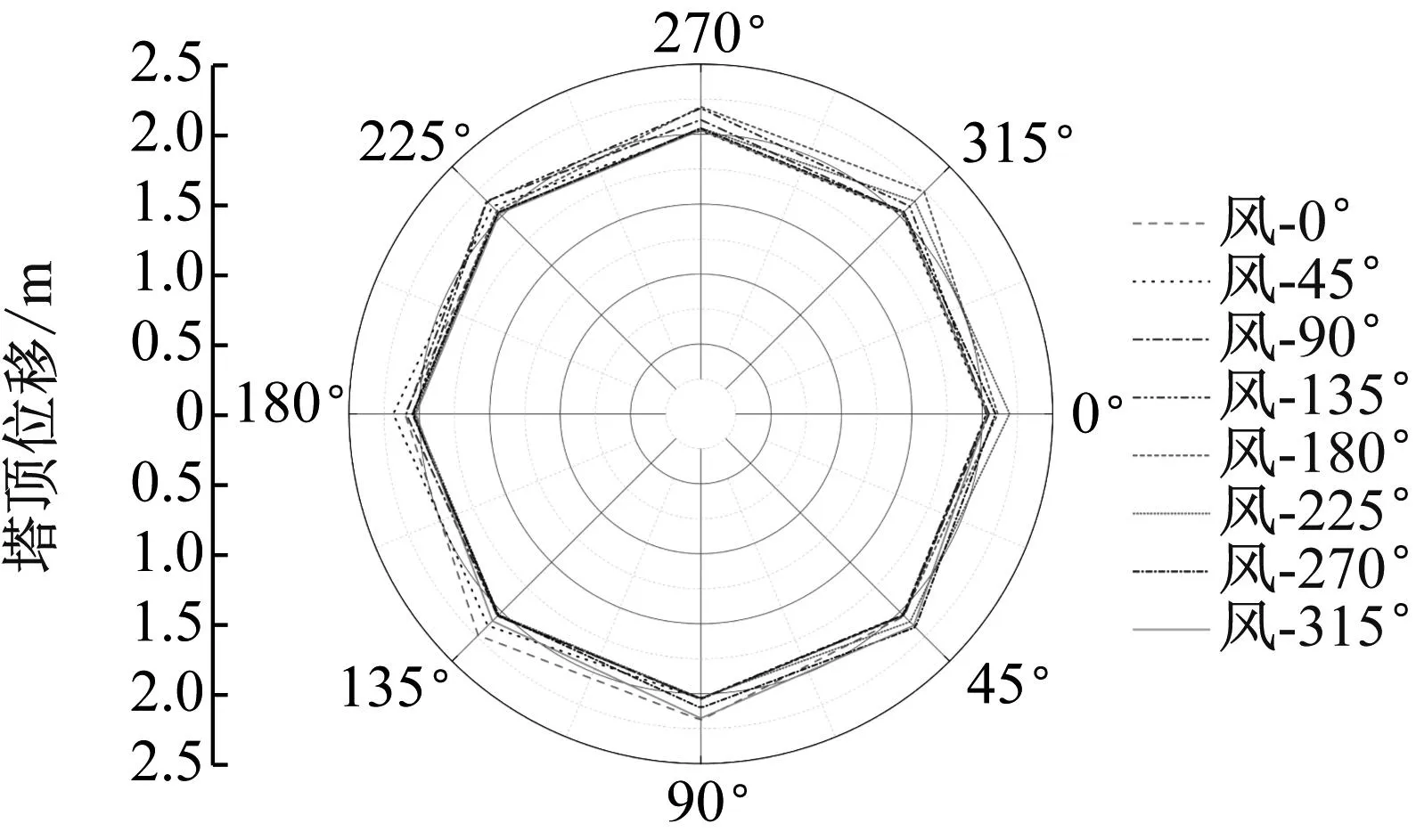
图16 风-Kobe波耦合作用下塔顶位移分布规律

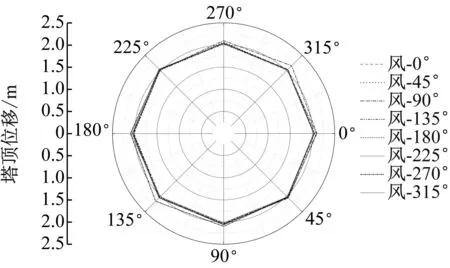
图17 风-Taft波耦合作用下塔顶位移分布规律

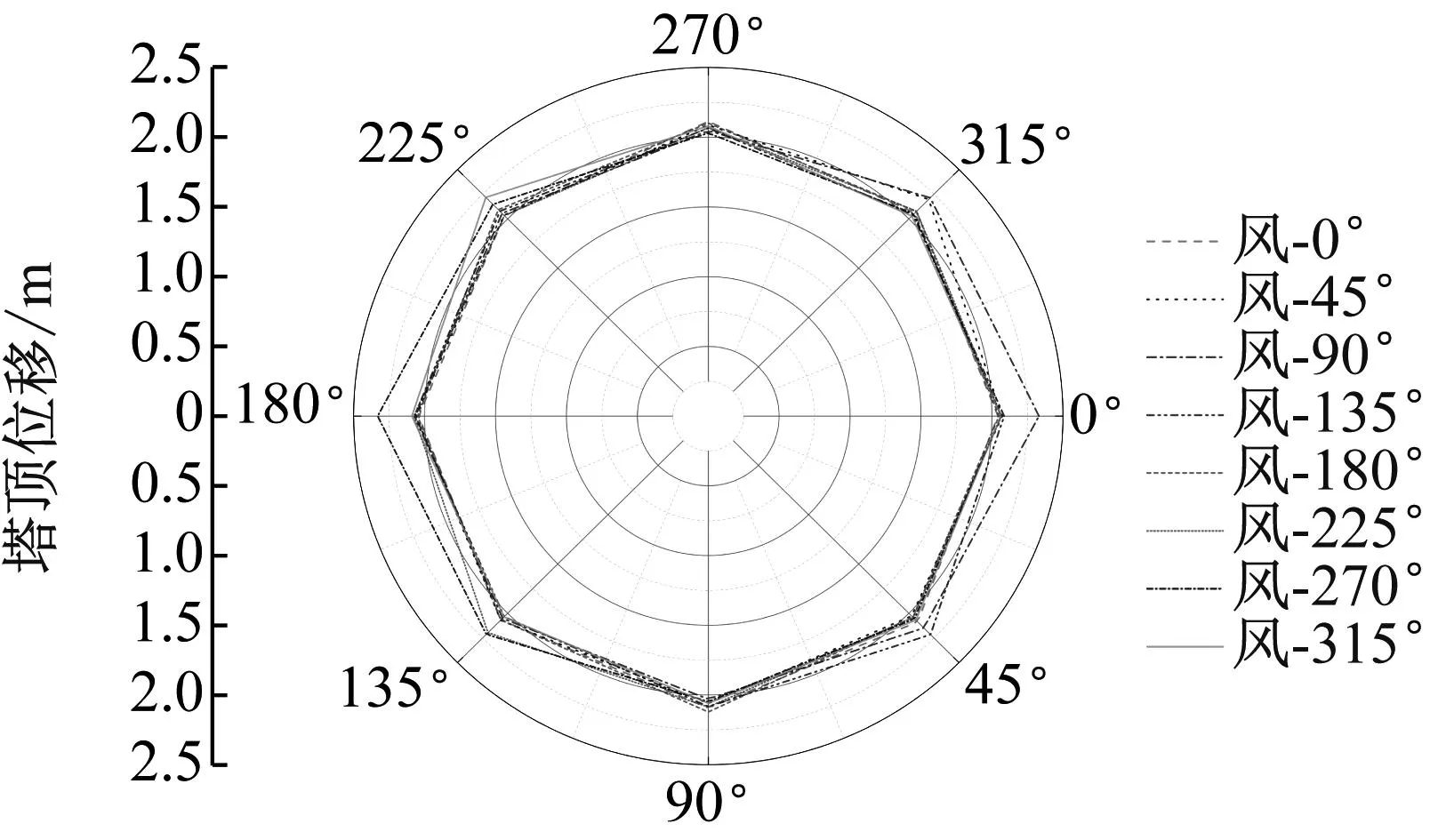
图18 风-EI Centro波耦合作用下塔顶位移分布规律

在确定某一风荷载输入角的前提下,地震从不同角度输入并引起风电塔筒门洞应力和基底应力的最大值,如图19～图21及图22～图24所示。相较图16～图18塔顶位移最值的分布规律,门洞应力最值及基底应力最值的分布则显得较离散且差异较大,且从图19和图22中可知,Kobe波相较其他两条地震波引起的门洞应力最值和基底应力最值更大。风荷载不同输入角度对门洞应力最值影响较大,而地震输入角的影响较小,风-震耦合作用下门洞应力的最值大于风荷载单独作用。风荷载输入角度及地震输入角度对于基底应力最值有重要影响,其中地震动更占主导作用,Taft波在315°输入耦合、风荷载在270°输入出现极大值情况,而Taft波的其他工况在各自地震波作用下对风向的输入角度不敏感,这显然更佐证了风-震耦合分析的必要性,此外,对比风和地震单独作用下引起的风电结构的门洞及基底应力,在风-震耦合作用下可能会导致风电塔筒强度方面的额外需求。

图19 风-Kobe波耦合作用下门洞应力分布规律

图20 风-Taft波耦合作用下门洞应力分布规律

图21 风-EI Centro波耦合作用下门洞应力分布规律

图22 风-Kobe波耦合作用下基底应力分布规律

最后,基于“最不利塔顶位移”、“最不利门洞应力”和“最不利基底应力”来确定风-震耦合作用下风电塔筒的最不利组合工况,结果如表4所示。从表4可知,对于风电塔筒在风-震耦合作用下的最不利情形,地震多是从315°或者0°输入,而风多是由90°、180°和270°输入。另外需要注意的是大多数风电结构在安装时门洞朝向是避开主风向的,然而这种做法可能会导致风电塔筒在风-震耦合作用下的一个最不利情形(见表4)。因此,风电从业人员在确定门洞朝向问题上不应简单地只考虑到风荷载的影响,更应考虑这种风-震耦合作用带来的影响并基于此确定门洞的朝向。

表4 风-震耦合下的最不利组合工况

3 风-震耦合作用下风电塔筒的动力屈曲分析

为深入探讨风-震耦合作用下风电塔筒是否会发生动力屈曲,本章基于第2章得到的9组最不利风-震耦合工况结合增量动力分析(incremental dynamic analysis,IDA)方法及绘制最不利工况下塔顶节点的相图来对风电塔筒的动力屈曲行为进行研究。

3.1 基于“最不利塔顶位移”的风-震耦合作用下风电塔筒响应分析

本节首先考察了基于“最不利塔顶位移”所确定的风-震耦合工况下风电塔筒的动力屈曲行为。首先是对地震动按照0.1g的增量进行调幅,再由ABAQUS软件输出风电塔筒的塔顶位移时程曲线进而绘出塔顶节点的相轨迹,最后利用相图对风电塔筒的动力屈曲行为作出判断,如图25～图27所示。图25(a)、图26(a)和图27(a)分别为风-Kobe波耦合、风-Taft波耦合和风-EI Centro波耦合作用下随着地震加速度峰值按0.1g的增量不断调幅直至塔顶相轨迹出现分岔的塔顶位移的相图, 而图25(b)、图26(b)和图27(b)分别为风-Kobe波耦合、风-Taft波耦合和风-EI Centro波耦合作用下风电塔筒发生动力屈曲时的应力有限元图。当风电塔筒发生动力屈曲时,Kobe波、Taft波和EI Centro波的加速度峰值分别是3.1g、1.9g和1.8g,风电塔筒最后均是产生了局部的塑性动力屈曲,屈曲部位都是处在塔筒第四节与第五节的连接处附近。对比图10～图12,发现EI Centro波引起的风电塔筒塔顶位移更大,这就导致其可能引起较大的几何非线性,在风-EI Centro波耦合作用下风电塔筒可能易发生动力屈曲。但是风-Taft波耦合工况与风-EI Centro波耦合工况导致风电塔筒发生动力屈曲所需地震加速度峰值十分接近且二者之间的差异仅体现在地震动本身的波形和地震输入夹角仅差45°,而风-Taft波耦合工况与风-Kobe波耦合工况导致风电塔筒发生动力屈曲所需地震加速度峰值差异很大且二者之间的差异体现在地震动本身的波形和风荷载作用夹角差90°。因此,导致风-Taft波耦合工况与风-Kobe波耦合工况引发风电塔筒动力屈曲的差异性主要因素还是风荷载的作用方向、叶轮与机舱的朝向和地震波本身的波形共同导致的。

(a) 塔顶节点相图

(a) 塔顶节点相图

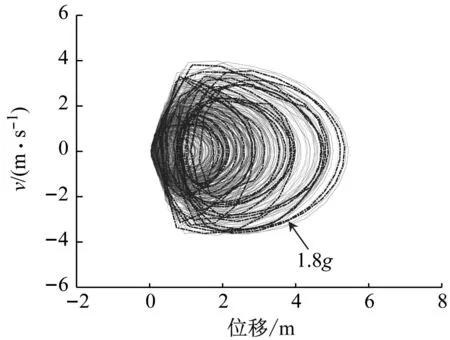
(a) 塔顶节点相图

最后,对比这三个工况下的局部屈曲部位的朝向可以发现,当塔筒发生局部的动力屈曲时其屈曲部位的朝向很大程度上都指向了地震动施加的角度,即地震动的作用方向,且风-Taft波耦合工况与风-EI Centro波耦合工况下风电塔筒发生动力屈曲的部位朝向不同,因此地震动在某种程度上应该主导着风电塔筒的破坏形式。

3.2 基于“最不利门洞应力”的风-震耦合作用下风电塔筒响应分析

同3.1节类似,本节则是探讨基于“最不利门洞应力”所确定的风-震耦合工况下风电塔筒的动力屈曲行为,如图28～图30所示。图28(a)、图29(a)和图30(a)分别为风-Kobe波耦合、风-Taft波耦合和风-EI Centro波耦合作用下随着地震加速度峰值按0.1g的增量不断调幅直至塔顶相轨迹出现分岔的塔顶位移相图, 而图28(b)、图29(b)和图30(b)分别为风-Kobe波耦合、风-Taft波耦合和风-EI Centro波耦合作用下风电塔筒发生动力屈曲时的应力有限元图。当风电塔筒发生动力屈曲时,Kobe波、Taft波和EI Centro波的加速度峰值分别是3.2g、2.0g和1.7g,风电塔筒最后均是产生了局部的塑性动力屈曲,屈曲部位都是处在塔筒第四节与第五节的连接处附近,总体上来说基于“最不利塔顶位移”所确定的风-震耦合工况比基于“最不利门洞应力”所确定的风-震耦合工况更不利。

(a) 塔顶节点相图

(a) 塔顶节点相图

(a) 塔顶节点相图

同样,风-Taft波耦合工况与风-EI Centro波耦合工况导致风电塔筒发生动力屈曲所需地震加速度峰值具有较小的差异且二者之间的差异仅体现在地震动本身的波形和地震输入夹角仅差45°。对比“最不利塔顶位移”下的风-Taft波耦合工况可知,“最不利门洞应力”下的风-Taft波耦合工况与“最不利塔顶位移”下的风-Taft波耦合工况差异仅体现在了风荷载作用夹角相差90°,但是二者引起风电塔筒动力屈曲所需地震动的加速度峰值却是极为接近的。再对比“最不利塔顶位移”下的风-Kobe波耦合工况可知,“最不利门洞应力”下的风-Taft波耦合工况与“最不利塔顶位移”下的风-Kobe波耦合工况差异仅体现在了地震波本身的不同,进而揭示了风电塔筒的动力屈曲发生的主导因素是地震波本身。对比“最不利塔顶位移”下的风-Taft波耦合工况、风-Kobe波耦合工况以及“最不利门洞应力”下的风-Taft波耦合工况下风电塔筒发生动力屈曲的应力有限元图可知,风的作用方向、叶轮和机舱的朝向也影响着局部屈曲的发展及塔筒的破坏形式,但就结合3.1节可知,地震动对于动力屈曲的发展及塔筒的破坏形式起主导作用。

3.3 基于“最不利基底应力”的风-震耦合作用下风电塔筒响应分析

最后,本节探讨基于“最不利基底应力”所确定的风-震耦合工况下风电塔筒的动力屈曲行为,如图31～图33所示。图31(a)、图32(a)和图33(a)分别是风-Kobe波耦合、风-Taft波耦合和风-EI Centro波耦合作用下随着地震加速度峰值按0.1g的增量不断调幅直至塔顶相轨迹出现分岔的塔顶位移相图,而图31(b)、图32(b)和图33(b)分别为风-Kobe波耦合、风-Taft波耦合和风-EI Centro波耦合作用下风电塔筒发生动力屈曲时的应力有限元图。当风电塔筒发生动力屈曲时,Kobe波、Taft波和EI Centro波的加速度峰值分别是3.9g、1.9g和1.9g,风电塔筒最后均是产生了局部的塑性动力屈曲,屈曲部位都是处在塔筒第四节与第五节的连接处附近。

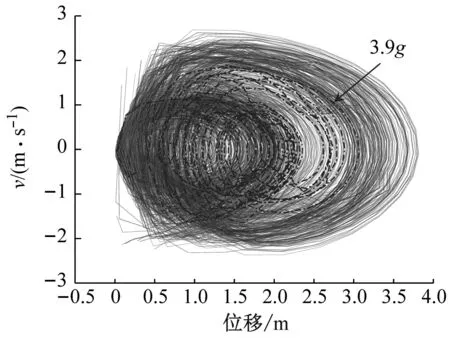
(a) 塔顶节点相图

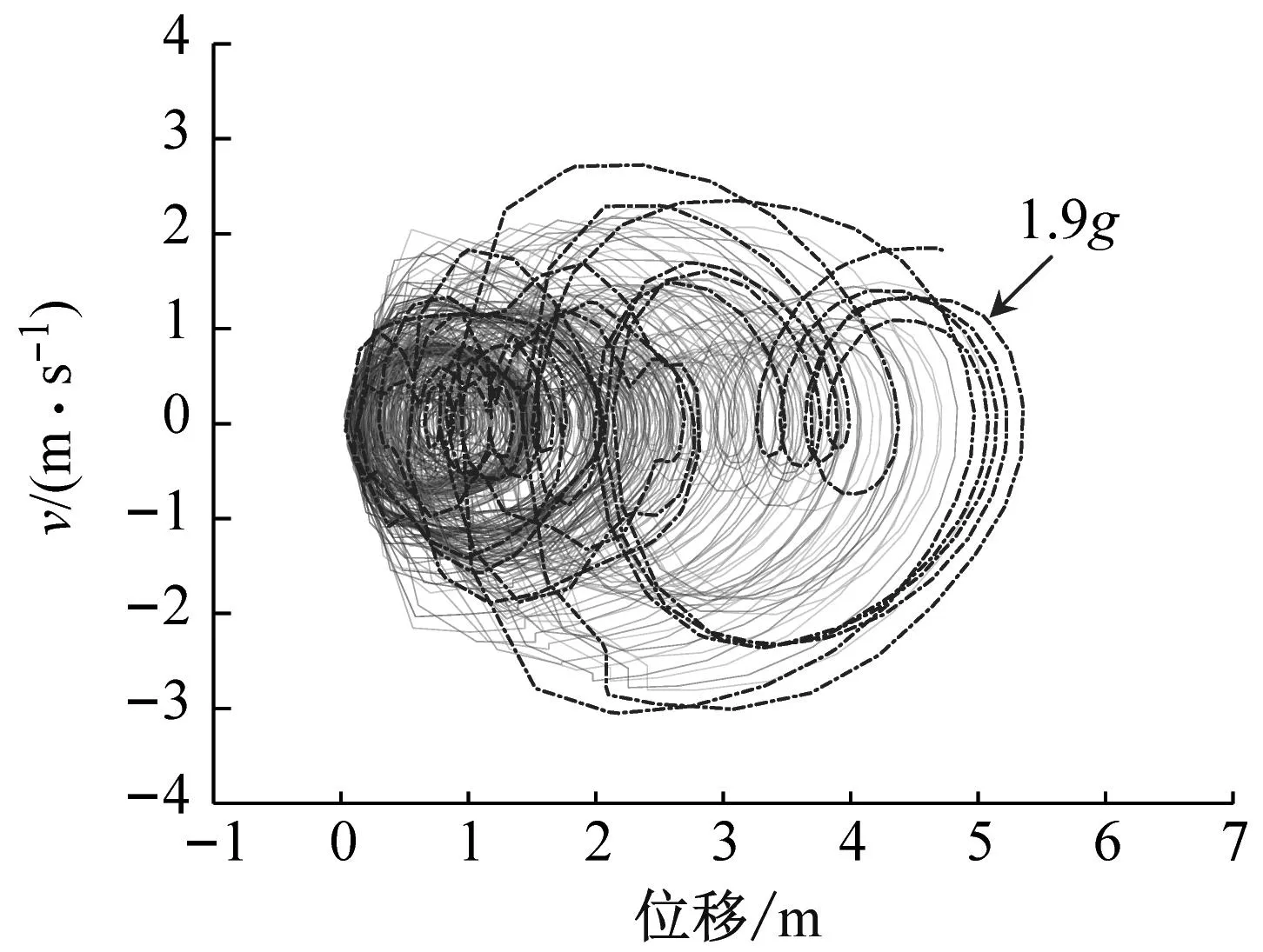
(a) 塔顶节点相图

总体上来说,基于“最不利塔顶位移”所确定的风-震耦合工况比基于“最不利基底应力”所确定的风-震耦合工况更不利。与3.1节和3.2节不同的是,基于“最不利基底应力”所确定的风-震耦合工况下风荷载的输入角度都是270°,其具有很好的一致性。结合图25(b)、图28(b)和图31(b)可知,在三种“最不利”风-Kobe波耦合的工况下,出现了风电结构发生局部屈曲的部位朝向基本上都在风荷载作用的方向上,而三种“最不利”风-Taft波耦合和“最不利”风-EI Centro波耦合的工况下并没有此现象,此时的风电塔筒局部屈曲的部位朝向既不指向风荷载作用方向也不指向地震输入方向。

此外,与3.1节和3.2节不同的是,本节的风-Taft波耦合工况和风-EI Centro波耦合工况下二者的风和地震的作用角度是一致的,且二者引起风电塔筒动力屈曲所需的地震加速度幅值也是一样的。为深入分析该点,本文又考察了单一方向上归一化的Kobe波、Taft波和EI Centro波的时域及频域分布,如图34所示。从图34可知,Taft波和EI Centro波的频谱分布较为相似,而Kobe波则与前两者有着较大的不同。因此,Taft波和EI Centro波在一定程度上应具有较大的相似性,而这也佐证了前两节所述的地震波本身对于风-震耦合作用下风电塔筒动力屈曲的发展及塔筒的破坏形式起主导作用。

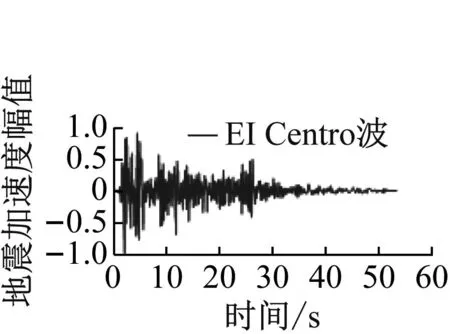
图34 单一方向上归一化的Kobe波、Taft波和EI Centro波的时域及频域分布

4 结 论

以西北地区某2.5 MW风力发电机为原型,在计算风电结构所受风荷载的基础上,通过将水平方向分为8个方向以及输入地震动的两个互相垂直的水平地震动分量来考虑风与地震的组合,并将叶轮平面始终考虑为与风向垂直。最后利用基于塔顶位移和门洞与基底处的应力来确定风电塔筒在风-震耦合作用下的最不利组合工况,提出“最不利塔顶位移相图法”来分析风电塔筒在风-震耦合作用下的动力屈曲行为并探讨其主导因素。通过研究分析表明:

(1) 在弹性范围内,叶轮和机舱的质心相对塔筒中心的偏心对于塔顶位移响应的影响基本不大,风荷载对于塔顶的位移响应具有主导性,风荷载对于塔筒门洞应力的影响相较地震动更具有主导性,而地震动对于基底应力的影响相较风荷载更具主导性。

(2) 在考虑机舱和叶轮朝向的条件下,不能简单地将风荷载和地震荷载分开考虑,二者的耦合可能会诱发较大的几何非线性,在风-震耦合作用下可能会导致风电塔筒强度方面的额外需求。

(3) 在确定门洞朝向问题上不应简单地只考虑到风荷载的影响进而避开主风向,其可能会导致风-震耦合下的不利情形。因此,应考虑风-震耦合作用的因素来确定门洞的朝向。

(4) 基于“最不利塔顶位移”的风-震耦合工况基本代表着最不利的情形;在风-震耦合作用下,风电塔筒基本上都呈现局部的塑性动力屈曲现象,而动力屈曲的发生及其发展与风荷载、机舱与叶轮的朝向及地震动本身有关,其中地震动对于局部屈曲的产生起主导作用;基于“最不利塔顶位移相图法”可以很好地判别并分析风电塔筒的动力屈曲。