单级直齿轮副的共存吸引子特性研究

金 花, 张子豪, 吕小红

(兰州交通大学 机电工程学院,兰州 730070)

齿轮传动是应用广泛的动力传动装置之一,其工作性能对机械系统有着重要的影响。因此,考虑齿侧间隙、质量偏心和时变啮合刚度等因素影响的齿轮系统动力学是机械工程界广泛关注的研究领域。由于单自由度系统的振动研究既有实践意义又有理论意义,因此单级直齿轮副的动力学研究引起了许多学者的关注。齿轮系统动力学的研究方法主要有增量谐波平衡法[1]、A-算符法[2]和分段多尺度法[3]等。Wei等[4]应用谐波平衡法和改进的区间谐波平衡法分别分析了具有确定参数和不确定参数单自由度齿轮系统的动力学。苟向锋等[5]应用数值计算的方法辨识了齿轮系统的周期行为模式及其在两参数空间的存在区域。Yang等[6]重构了单自由度齿轮系统动力学的时变啮合刚度和静态传递误差模型。郜志英等[7]应用伪不动点追踪法分析了齿轮系统周期解的稳定性与分岔。

擦边分岔是非光滑系统特有的一种分岔。高建设等[8]发现齿面擦边接触会使齿轮传动系统的运动周期、啮合力以及冲击状态发生变化。尹桩等[9]研究了齿轮啮合运动的擦边行为,发现擦边分岔不改变相轨迹的拓扑结构。

共存吸引子[10]和混沌激变[11]是非光滑系统中常见的两种全局现象。唐进元等[12]应用图胞映射法计算了齿轮系统共存吸引子的全局特性。Shi等[13]计算了单自由度齿轮副在两参数平面的多稳态行为。已有关于齿轮系统全局动力学的研究报道主要集中在稳定周期解和混沌等终态吸引子的动力学,很少考虑不稳定吸引子的存在性,因此,一些隐藏的稳定周期吸引子不能被发现,系统的全局动力学不能被完全揭示。为了能够为齿轮副参数设计与优化提供理论依据,很有必要对齿轮系统共存吸引子(包括稳定和不稳定)的动力学进行研究。

打靶法是一种求解非线性系统周期解及稳定性的常用方法[14]。近年来,研究者应用延续算法在非光滑系统动力学领域取得了许多重要的成果[15-17]。本文结合初值胞映射法和打靶法求解单级直齿轮副的共存吸引子及其稳定性,用延续算法和数值仿真方法追踪吸引子的分岔,应用胞映射法分析吸引子的吸引域演化,研究系统的共存吸引子特性以及鞍结型擦边分岔和混沌激变等不连续分岔行为,充分揭示系统的全局动力学,为直齿轮副动力学行为的评价以及参数设计与优化提供指导,为直齿轮副乃至整个机械系统的安全运行和故障预警等提供参考。

1 齿轮副动力学模型

单级直齿轮副的力学模型如图1所示。Ii、rbi和θi(i=1,2)分别为主、从动齿轮的转动惯量、基圆半径和扭转角位移。Cg为啮合阻尼。非线性因素考虑时变啮合刚度和综合传递误差,分别为K(t)和e(t)。非光滑因素考虑齿侧间隙为2D。系统的无量纲运动微分方程可表示为

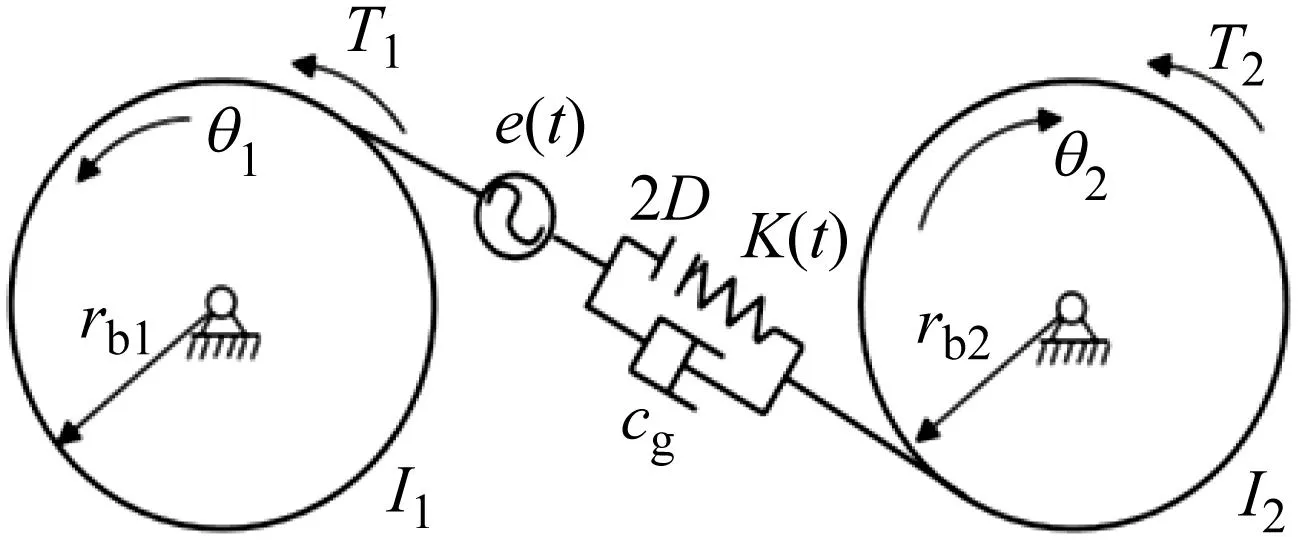
图1 直齿轮副的力学模型

(1)

式中:ξ为阻尼比;k为时变啮合刚度幅值;ε为误差波动幅值;F为无量纲扭矩;ω为无量纲啮合频率;g(x,d)为间隙函数。无量纲处理时,一般将D作为标称尺度,此时d=1,则间隙函数为

(2)

2 共存吸引子的求解与追踪方法

若周期轨线由点u0∈G1出发经过时间T=2nπ/ω后返回u0点,其运动轨迹为G1→G2→G3→G2→G1,则Poincaré映射及其Jacobi矩阵分别为

(3)

(4)

式中:PDi为矩阵微分方程式(5)中∂u(t)/∂ui0在t=t1时的解,其中t1为系统在子空间Gi运动的时间。

(5)

设分岔参数为v,其余参数值固定,共存吸引子的求解与追踪方法描述如下。

(1) 结合初值胞映射法和基于Poincaré映射的打靶法求解v=v0时的共存吸引子。在Poincaré截面上选取一个待考察的状态空间,然后网格化。以网格线的交点作为初始不动点,应用打靶法求解v=v0时Poincaré截面上的不动点,即系统的周期吸引子。通过式(4)和式(5)计算Jacobi矩阵PD的特征值,根据Floquet理论确定周期吸引子的稳定性。待循环计算完所有网格线的交点,便可得到系统共存的周期解及其稳定性。

(2) 以v=v0时的周期吸引子为初始不动点,应用延续算法递减递增分岔参数v追踪该吸引子在v∈[v1,v0]及v∈[v0,v2]内的分岔演化。待所有共存的周期吸引子追踪完毕,便可得到系统在v∈[v1,v2]内的全局动力学。

(3) 应用4阶变步长Runge-Kutta法数值仿真系统在v∈[v1,v2]内的稳定周期运动及其分岔,验证数值延拓结果的正确性并得到混沌响应。

3 共存吸引子的稳定性与分岔

取系统参数(1):k=0.1,ε=0.2,ξ=0.04和F=0.05,应用初值胞映射法和延拓打靶法求解系统在ω∈[0.20,1.20]的共存周期吸引子及其稳定性与分岔,应用数值仿真验证数值延拓结果的正确性并得到混沌响应。兴存吸引子的分岔图,如图2所示。两种计算结果的合成分岔图见图2(a)。图2(c)～图2(i)为图2(a)的细节描述。图2中,实线为稳定的周期吸引子,虚线为不稳定的周期吸引子;圆点为分岔点;GR、PDi和SNi分别为擦边、周期倍化和鞍结分岔,下标i为同一类型分岔的发生次序;用P1、Q1、R1、S1和T1区分处于不同分支的稳定周期1吸引子,不稳定周期吸引子用下标‘U’区别。图2(b)为ω递增和递减变化时数值仿真得到的分岔图。对比图2(a)和图2(b)可知,单级直齿轮副存在大量的多吸引子共存行为。但是,目前被广泛采用的数值仿真方法和单参数延拓方法隐藏了许多重要的吸引子信息。因此,结合多种方法研究直齿轮副的共存吸引子及其稳定性与分岔对全面揭示系统的全局动力学至关重要。

(a) 合成分岔图

由图2可知,鞍结分岔(SNi)使周期吸引子成对出现或消失,而周期倍化分岔(PDi)使周期吸引子失去或获得稳定。稳定的周期1吸引子P1、Q1、R1和S1存在的ω区间分别为(0.20,0.472 476 76)、(0.275 010 55,0.931 868 68)、(0.312 704 37,0.472 921 97)和(0.323 548 48,0.502 913 07),见图2(a)。当ω=0.395 0时,9个周期吸引子共存,分别是4个稳定的周期1、3个不稳定的周期1、1个稳定的周期4和1个不稳定的周期4,其相轨迹和Poincaré映射,如图3所示。图3中:相轨迹与对应图2吸引子相同;实线和虚线分别为稳定和不稳定周期运动的相轨迹;圆点为Poincaré映射不动点。P1运动表现为完全齿面啮合运动,为简谐响应。其余周期运动由于出现脱啮以及齿背啮合状态,响应受到间隙的影响成为非简谐响应。在啮合过程中,周期1运动Q1和S1U以及周期4运动P4和P4U既有齿面啮合又有齿背啮合。

(a)

图2(a)中矩形区域①内的P1、Q1和R1吸引子分支非常贴近,不能明显区分,因此,图2(c)描述了P1与Q1吸引子的分岔,图2(d)为R1和R1U吸引子的分岔。由图2(c)知,增大ω,P1吸引子在ω≈0.470 0时发生了跳跃分岔。减小步长延拓追踪P1吸引子在跳跃点附近的详细动力学,结果见图2(e)。随着ω的递增,P1吸引子发生鞍结型擦边分岔(GR-SN1),使系统的稳定周期1响应产生跳跃。GR点与SN1点之间的距离Δω=0.000 545 16。当ω=0.471 931 60(GR)时,P1运动的相轨线与边界∑1相切,系统发生擦边分岔使周期1完全啮合运动变为周期1啮合-脱啮运动。随后在ω=0.472 476 76(SN1)处,P1吸引子经鞍结分岔失去稳定性,产生向ω减小方向延续的不稳定周期1吸引子P1U。此后,减小ω。当ω=0.457 232 32(SN2)时,系统再次发生鞍结分岔,P1U吸引子变为稳定,用T1表示。同时,参数ω恢复递增的变化方向。

Jiang等分析了碰撞系统擦边诱导的鞍结分岔和周期倍化分岔。目前,关于齿轮系统擦边诱导的分岔研究还未见报道。有研究发现擦边分岔使图2中系统的响应发生跳跃。由图2(e)可知,跳跃是由于系统发生了擦边诱导的鞍结分岔SN1,引起P1与T1吸引子转迁过程中的迟滞。擦边分岔GR是连续的。这个特征与分段线性系统的鞍结型擦边分岔特征相同。

当ω=0.481 737 37(PD1)时,T1吸引子经周期倍化分岔产生共存的不稳定周期1吸引子T1U和稳定周期2吸引子T2。延拓追踪T1U吸引子,在ω=0.506 465 46(PD2)和ω=0.508 750 000(SN3)时,Floquet特征乘子分别为λ1=0.767 44,λ2=1.000 09和λ1=-1.000 52,λ2=-0.779 87,T1U吸引子经周期倍化分岔PD2恢复稳定,随后在SN3点与不稳定周期1吸引子Q1U碰撞并消失。通过数值仿真发现,T2吸引子经周期倍化序列通向短暂的混沌,然后该吸引子的分岔突然终止。

由图2(d)可知,R1和R1U吸引子的分岔行为非常简单。两个吸引子在ω=0.312 704 37(SN4)和ω=0.472 921 97(SN5)时经鞍结分岔同时出现或消失。

图2(f)描述了图2(c)所示小区域⑤的细节。可见,在ω=0.275 010 55(SN6)时,系统经鞍结分岔产生一对新的周期1吸引子V1和Q1U。Q1U吸引子分支终止于SN3点。V1吸引子存在的ω区间非常窄。当ω=0.275 350 50(PD3)时,系统发生周期倍化分岔使V1吸引子变为不稳定吸引子V1U,然后在ω=0.308 476 67(PD4)时经周期倍化分岔变为稳定的Q1吸引子,见图2(c)。

由图2(a)可知,在ω=0.323 548 48(SN8)时,系统出现与P1、Q1、Q1U、R1和R1U吸引子共存的S1和S1U吸引子。用延续算法分别追踪S1和S1U吸引子,S1U吸引子在ω=0.931 868 68(SN7)时与Q1吸引子碰撞并消失;S1吸引子在ω=0.502 913 07(PD5)时经周期倍化分岔失稳。

图2(g)为图2(a)所示矩形区域②的局部放大。可见,系统在区域②内出现周期4吸引子的分岔分支。为了详细描述周期4吸引子的分岔演化,图2(h)描述了图2(g)中区域⑥的细节。由图2(g)和(h)可知,增大ω,当ω=0.361 546 18(SN9)时,系统发生鞍结分岔产生1个稳定的和1个不稳定的周期4吸引子,分别为P4和P4U。增大ω,P4吸引子在ω=0.361 551 81(PD6)处发生周期倍化分岔。数值仿真结果显示,P4及其周期倍化序列演化的吸引子存在的ω区间非常窄。用延续算法追踪P4U吸引子,在ω=0.403 454 55(SN10)时,P4U吸引子经鞍结分岔获得稳定。此后,ω的变化方向由增大变为减小。当ω=0.400 587 00(PD7)时,稳定的周期4吸引子经周期倍化分岔失稳,然后在ω=0.393 438 30(PD8)时又恢复稳定。

图2(i)为图2(a)所示小区域③的放大。由图2(a)和(i)可知,在ω=0.607 492 09(SN11)时,系统经鞍结分岔出现1个稳定的和1个不稳定的周期2吸引子,分别为P2和Q2U。增大ω当ω=0.607 512 82(PD9)时,P2吸引子经周期倍化分岔失稳变为P2U吸引子。然后,P2U与Q2U吸引子共存,一直持续到ω=1.20。

4 混沌激变

由图2可知,随着分岔参数的变化,稳定的周期吸引子或经鞍结分岔消失,或经一系列分岔演化为混沌。混沌边界激变是对应周期吸引子的分岔突然终止的一个重要因素。当ω∈(0.640 330 00,0.931 868 68)时,混沌吸引子与稳定的周期1吸引子Q1共存,而在ω∈(1.169 210 00,1.20)时,混沌吸引子与稳定的周期2吸引子Q2共存。减小ω,当ω=1.169 210 00和ω=0.640 330 00时,系统发生边界激变导致混沌吸引子突然消失。为分析边界激变的分岔结构,应用胞映射法计算了共存吸引子的吸引域,如图4所示。

(a) ω=0.80

当ω=0.70时,5个周期吸引子(1个稳定)和1个混沌吸引子共存。稳定周期1吸引子Q1与混沌的吸引域见图4(b)。图4中:各吸引子与对应图2吸引子相同;圆点为稳定的周期吸引子;“▲”为不稳定的周期吸引子;Q1为吸引子的吸引域,Q1吸引子在全局范围内是稳定的,系统响应对初始条件的扰动不具有敏感性。增大ω,混沌吸引子的吸引域逐渐扩张压缩Q1吸引子的吸引域,见图4(a)和(b)。当ω=0.931 868 68(SN7)时,Q1吸引子与S1U吸引子碰撞导致Q1吸引子及其吸引域消失。相反,当ω减小时,混沌吸引子向中心收缩,导致位于吸引域边界上的S1U吸引子向混沌吸引子逐渐靠近,见图4(c)和(d)。其中,图4(c1)为图4(c)的局部放大。当ω=0.640 330 00时,混沌吸引子与S1U吸引子碰撞,系统发生边界激变导致混沌吸引子及其吸引域突然消失,系统的终态响应只表现为Q1运动。

当ω∈(1.169 210 00,1.20)时,4个周期吸引子(1个稳定)与1个混沌吸引子共存。终态吸引子的吸引域演化见图4(e)～图4(g)。图4(e)为ω=1.20时的吸引域。不稳定周期2吸引子Q2U位于吸引域边界。2个吸引域互相环绕且有散点,边界具有分形特征,说明吸引子对初始条件具有较高的敏感性,Q2吸引子只在局部区域内稳定。减小ω,Q2吸引子的吸引域缓慢地向中心收缩导致位于吸引域边界上的Q2U吸引子向混沌吸引子逐渐靠近,见图4(f)和(g)。当ω=1.169 210 00时,混沌吸引子与Q2U吸引子碰撞,系统发生边界激变导致混沌吸引子及其吸引域突然消失。

取系统参数(2):ω=0.50,ε=0.2,ξ=0.05和F=0.1,应用初值胞映射法、延拓打靶法以及数值仿真计算系统随时变啮合刚度幅值k变化的合成分岔图如图5所示。图5中,BC和IC分别为边界激变和内部激变。

图5 参数(2)条件下的分岔图

增大k,当k=0.214 967 68(SN1)时,鞍结分岔使系统出现2个新的周期2吸引子(1个稳定,1个不稳定)。此后,3个周期2吸引子与1个不稳定周期1吸引子共存。当k=0.429 255 51(SN2)时,系统再次发生鞍结分岔,产生于SN1点的不稳定周期2吸引子与产生于PD1(k=0.049 567 51)点的稳定周期2吸引子碰撞并消失,系统表现为1个稳定的周期2吸引子与1个不稳定的周期1吸引子共存。继续增大k,稳定的周期2吸引子经开始于k=0.474 697 47(PD2)的周期倍化序列通向混沌。在PD1和PD2点失稳的不稳定周期吸引子一直持续到k=1.80。

当k=0.859 977 29(SN3)时,鞍结分岔再次使系统出现2个新的周期2吸引子。其中,稳定周期2吸引子的出现破坏了混沌吸引子的完整吸引域,使系统在极小部分初值下的终态跳跃为周期2运动。此后,4个周期吸引子(1个稳定)与1个混沌吸引子共存,吸引域如图6所示。取k=0.87,共存吸引子及终态吸引子的吸引域见图6(a)。图6(a)中:圆点为稳定的周期2吸引子;“▲”为不稳定的周期吸引子。产生于SN3点的不稳定周期2吸引子位于吸引域边界,而产生于周期倍化分岔点PD1和PD2的2个不稳定周期吸引子位于混沌吸引子的吸引域内。增大k,周期2吸引子的吸引域逐渐扩大,混沌吸引子逐渐长大向吸引域边界靠近,见图6(a)～图6(c)。在BC处,混沌吸引子与位于吸引域边界上的不稳定周期2吸引子碰撞,系统发生边界激变导致混沌吸引子及其吸引域突然消失,系统的终态只表现为周期2运动,见图6(d)。

(a) k=0.87

继续增大k,稳定周期2吸引子经开始于k=1.141 818 21(PD3)处的周期倍化序列通向混沌。混沌吸引子及其吸引域见图6(e)。图6(e)中,“▲”为产生于SN3点的不稳定周期2吸引子。混沌吸引子包含两个窄带部分。进一步增大k,混沌吸引子突然变大,见图6(f),这是混沌内部激变(IC)的结果。该激变过程中,混沌吸引子没有与其吸引域内部的不稳定周期行为发生碰撞,这个特性不同于光滑动力系统的内部激变特性。

鞍结分岔产生的不稳定周期吸引子可能位于吸引域边界,而经周期倍化分岔失稳的不稳定周期吸引子肯定位于吸引域内部。周期倍化分岔不会造成吸引子吸引域的拓扑结构和形状发生变化,不影响吸引子的全局稳定性。鞍结分岔产生新的稳定周期吸引子,改变了旧吸引子的吸引域结构,使系统在极小部分初值下的终态发生跳跃。当分岔参数变化时,混沌吸引子与鞍结分岔产生的位于吸引域边界的不稳定周期轨道发生碰撞,系统发生边界激变导致混沌吸引子及其吸引域突然消失。

5 结 论

以单级直齿轮副为研究对象,考虑时变啮合刚度、综合传递误差和齿侧间隙等非线性或非光滑因素,研究了系统丰富而复杂的全局动力学。选择Poincaré截面,应用初值胞映射法、延拓打靶法以及数值仿真求解并追踪系统的共存吸引子及其演化,揭示系统在极小参数区间存在的容易隐藏的吸引子信息;构建Poincaré映射,求解其Jacobi矩阵的特征值,根据Floquet理论确定周期吸引子的稳定性与分岔类型,研究了共存吸引子的周期倍化、鞍结和鞍结型擦边等分岔行为。应用胞映射法计算周期吸引子与混沌吸引子共存时的吸引域,揭示了齿轮系统的两种激变现象:边界激变和内部激变。

(1) 在一定参数条件下,单级直齿轮副存在大量的多吸引子共存现象。鞍结分岔使周期吸引子成对出现或消失,而周期倍化分岔使周期吸引子失去或获得稳定。边界激变导致混沌吸引子及其吸引域突然消失,对应周期吸引子的分岔突然终止。

(2) 直齿轮副属于分段非线性系统。由于非光滑因素的影响,系统会发生鞍结型擦边分岔。擦边分岔是连续的,但擦边诱导的鞍结分岔使系统终态发生跳跃,并引起迟滞现象。这个特征与分段线性系统的鞍结型擦边分岔特征相同。

(3) 位于吸引域边界上的不稳定周期吸引子只能由鞍结分岔产生。当分岔参数变化时,混沌吸引子与位于吸引域边界的不稳定周期轨道发生碰撞使系统发生边界激变。然而,在内部激变过程中,混沌吸引子没有与其吸引域内部的不稳定周期轨道发生碰撞,这个特性不同于光滑动力系统的激变特性。

本研究为全面揭示单级直齿轮副的动力学提供一个新的视角,研究结果为齿轮副参数设计与优化提供理论依据,为直齿轮副乃至整个机械系统的安全运行和故障预警等提供参考。