利用GeoGebra开展数学实验教学

吴玮　张姝

摘 要：GeoGebra软件易操作、高精度、交互性、易分享的特征，使其成为高效开展数学实验教学的重要工具。借助GeoGebra开展数学实验教学，要具体制作实验工具，动态演示图形变化，具象表示抽象符号，显化数学探究过程。同时，要注意平衡工具支持和自主探索的关系以及模拟实验与真实实验的关系。

关键词：小学数学；数学实验；GeoGebra

*本文系江苏省教育科学“十四五”规划2022年度重点课题“智能学习环境下小学数学实验教学研究”（编号：B/2022/03/62）的阶段性研究成果。数学实验教学是指为了获得数学知识，验证数学猜想，解决数学问题，让学生运用一定的方法和手段、工具和载体，在实验目的的引领下，进行规范的实验操作，并帮助学生通过数学化分析，建构数学意义，发展数学思维，培育创新意识的活动。［1］《义务教育数学课程标准（2022年版）》在“教学建议”中明确提出：“利用数学专用软件等教学工具开展数学实验，将抽象的数学知识直观化，促进学生对数学概念的理解和数学知识的建构。”［2］在小学数学教学中，笔者常常利用GeoGebra这一数学专用软件开展数学实验教学。

一、GeoGebra软件的特征

GeoGebra是将几何、代数、表格、作图、统计、微积分等以直观易用的方式集于一体，进行动态演示的一种交互式数学软件。相较于常规的实物学具以及类似的几何画板软件，GeoGebra软件的以下特征使其成为高效开展数学实验教学的重要工具。

（一）易操作

数学实验的重要价值在于让学生在“做中学”，便于学生操作的实验工具是数学实验教学的基本条件。与其他交互式数学软件相同，GeoGebra可以便捷地使用工具绘制各种图形，并且绘制的图形蕴含清晰的数学关系。例如，经过合理的设置，拖动线段时可以只发生平移、旋转的操作，而不改变线段的长度（模拟小棒）。此外，通过设置，可以控制界面在操作时是否会发生移动、缩放，从而避免学生的误操作。这些特点使得GeoGebra能够保障数学实验教学过程中学生操作的便捷性。

（二）高精度

实证性是数学实验的重要价值，高精度的实验工具会让实验操作更加规范。GeoGebra具有高精度的天然优势，具体体现在操作的高精度、测量的高精度与运算的高精度。例如，利用GeoGebra拖动图形时，可以设置平移模式是“自由移动”还是“固定网格”，后者可以实现图形的精准对齐；绘制图形时，可以通过测量功能直接标示有关的长度、角度、面积等，改变图形时，也会实时反馈测量数据；在数据加工方面，可以直接采用测量的数据通过编制的公式得到运算的结果，从而避免收集大量实验数据加工时带来的误差或错误。

（三）交互性

GeoGebra具备丰富的指令库，设置之后可以点击按钮执行或自动执行。例如，可以通过“滑动条”“输入框”等输入参数，再点击按钮执行指令绘制图形；也可通过指令实现分割、合并、比较等操作。合理运用指令，能够拓展实验工具的交互方式，使得实验工具可以为学生点拨实验过程中可能存在的问题，帮助学生通过实验建立数学化的分析。广泛研究表明，小学数学教学中，交互工具的运用有利于学生自主学习、探究学习和合作学习，在培养学生的思维能力和实践能力方面发挥着积极的作用。［3］

（四）易分享

相较于几何画板，GeoGebra具有免费开源、全平台的特征，使其无须下载软件，可直接通过网页打开。用其制作的具体实验工具还可以方便地发布为网页格式，通过链接或二维码等方式方便地推送到学生的终端，让每个学生都可以独立尝试、互不干扰，极大地简化了数学实验教学之前的准备工作和之后的整理工作，促进了数学实验教学的常态实施。这一特点也使得GeoGebra不同于几何画板多用于教师的课件演示，成为学生看得见、摸得着、促思考的数学实验工具。

二、利用GeoGebra开展数学实验教学的实践探索

（一）具体制作实验工具

虽然GeoGebra易操作，但是为了提高数学实验教学的效率，教师通常还是要针对具体实验的需求，制作相应的实验工具（特别是对于那些比较复杂的操作对象，应该事先完成制作），从而免去学生不必要的思考与操作，使得学生可以简单地扫码打开实验工具（包括一键重置初始状态），符合直觉地操作实验工具（包括软件自动测量数据、加工数据、提示操作规范性等），更加清晰地观察实验结果（包括局部缩放、三维视角旋转等）。

例如小学阶段常用的数学实验工具钉子板，学生的操作、判断容易受到皮筋的弹性、粗细和钉子板的大小等因素的影响。如果使用打印的点阵图，则所画的图形不能调整，只能重画，还可能因为学生作图能力的差异，影响实验探究。利用GeoGebra制作的“釘子板”工具很好地解决了上述问题。其打开后的界面主体是一个点阵图，周边有一些工具与按钮。其中，“多边形”工具（图标为）可以方便地绘制图形，“拖动”工具（图标为）可以调整图形的形状和位置，“面积”工具（图标为）可以快速测量得到面积，“移动视图”工具（图标为）和“缩放”按钮（图标为）方便观察图形，“删除”工具（图标为）以及“重置”按钮（图标为）可以清除图形。由此，学生围出图形、调整图形、计算面积等的过程都得到了优化。还可以根据实验需要增减工具或添加预设图形，如低年级学生使用时可以隐藏“面积”工具，保证了实验工具在具有普适性的同时还具有一定的针对性。

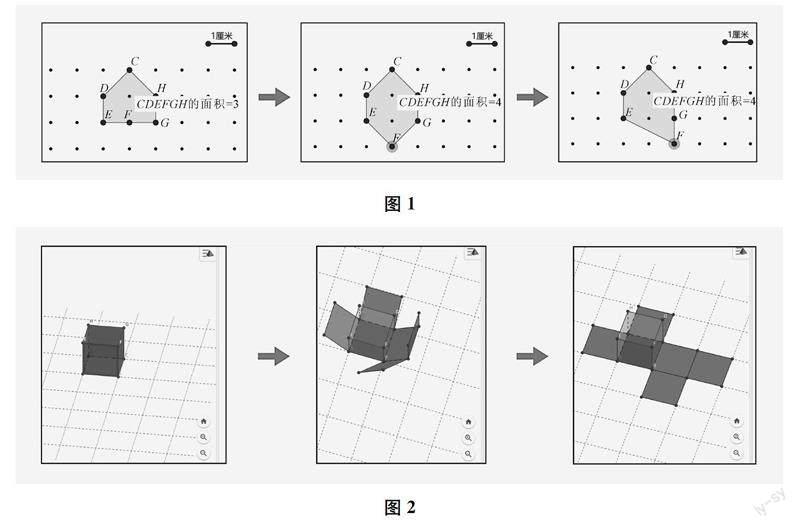
不仅如此，智能化的“钉子板”工具还创造了更多的实验验证方式。教学苏教版小学数学五年级上册《钉子板上的多边形》一课，利用工具实时测量面积的特点，可以先标示图形的面积，再通过拖动点来改变图形的形状（如图1所示），从而发现边上钉子数不变，图形内钉子数每多1，面积就增加1 cm2。

（二）动态演示图形变化

除了精准绘制图形，动态演示图形的变化是GeoGebra处理几何对象的重大优势（可以达到实物操作很难达到的灵活、精细效果）。这不是简单地播放动画，而是交互下的“动静结合”。在数学实验教学中，教师可以让学生自主操作利用GeoGebra制作的实验工具，调节其中图形的动静状态，借助图形的变化，多角度、全方位地观察图形的特征，帮助学生建立丰富的直观表象，认识重要的几何概念，发展空间观念。

例如，教学苏教版小学数学六年级上册《长、正方体的展开图》一课，利用GeoGebra制作的实验工具，让学生可以在拖动滑动条的过程中观察正方体六个面展开的全过程，也可以随时暂停观察展开过程中的状态，还可以在反复操作中观察每个面的连接关系，发现其在展开图中的位置（如图2所示）。

（三）具象表示抽象符号

相比于空间形式，数量关系更具有一般性（空间形式中也有数量关系），更体现数学的本质。数量是对现实生活中事物量的抽象，数是对数量的进一步抽象。［4］抽象的数量及数通常用符号来表示，即形式化。这种抽象性与形式化因为不可感，给数学学习（特别是儿童的数学学习）带来了很大的困难。数学实验通过将形式抽象的符号用直观具象的

事物表示，使其可感，帮助学生借助操作与观察，理解、发现其表示或蕴含的数量关系。而利用GeoGebra可以方便、快捷地将数用形表示，实现数学实验的功能。对此，教师在数学实验教学中也应该多加利用。

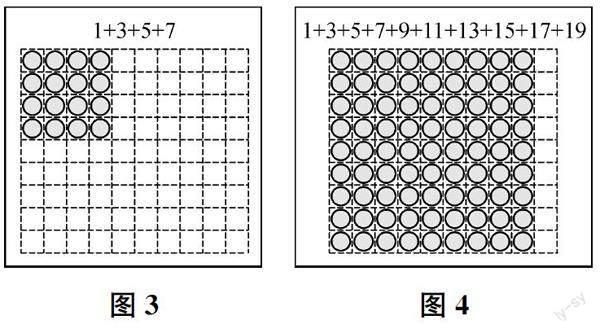
例如，教学“连续奇数求和”的问题时，可以引导学生利用GeoGebra进行实验探究。先研究1+3+5+7，引导学生通过按一定的方式摆数，发现可用“正方形”对这一算式进行表征（如图3所示），从而形成1+3+5+7=4×4的直观认识。再依次增加从1开始连续奇数的个数，让GeoGebra按照规律自动摆数（如图4所示）。学生经历观察、比较、推理的过程，不难发现：从1开始连续奇数的个数即为该“正方形”的边长，从1开始连续奇数的和则为该“正方形”的面积。

（四）显化数学探究过程

理解数学知识不仅要知其然，而且要知其所以然，关键是要经历数学知识的探究发现过程。数学实验是数学探究的重要方式，可以显化内隐的数学思维，让学生借助直观感知，通过分析比较，提炼数学本质。而GeoGebra可以更好地显化数学探究过程：一是操作容易留痕，可以对比呈现操作前后的变化；二是数据容易采集，可以精确分析定量的数学结论；三是案例更为全面、多样，使得归纳提炼更为容易，所得结论也更有力。

例如，教学苏教版小学数学六年级下册《面积的变化》一课，研究将长方形按比例放大后对应边长比与面积比之间的关系时，可以引导学生利用GeoGebra进行实验探究：自主绘制图形并拖动放大，观察比较放大前后的图形情况；同时自动呈现实验数据，分析放大前后的数量关系。然后，可引导学生对正方形、三角形、圆、梯形等一系列图形进行实验探究，从而提炼得到面积比是边长比的平方的结论。舍弃了画图、测量、计算等次要活动，凸显的探究过程更加清晰、完善，探究结果也就更容易理解。

三、利用GeoGebra开展数学实验教学的注意事项

第一，平衡工具支持和自主探索的关系。要避免实验工具过于强大而挤占学生的探索空间或替代学生的思维过程。利用GeoGebra开展数学实验教学时，不妨分阶段加入智能化功能：初始阶段提供基础功能，让学生完整地经历实验过程；后续阶段加入智能支持，优化实验操作，帮助学生丰富实证材料。

第二，平衡模擬实验与真实实验的关系。要避免模拟实验滥用而妨碍真实实验价值的发挥。例如，“可能性”“球的反弹高度”“大树有多高”等问题都需要在真实环境下进行实验，才能得到可靠的结论。此时，模拟实验可以作为后续的补充，在真实实验的基础上建立理想模型，提高研究价值。

参考文献：

［1］ 潘小福，蒋敏杰.常态化实施小学数学实验教学的策略［J］.江苏教育，2022（41）：7-11.

［2］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：89.

［3］ 凌秋虹.基于“交互工具”进行小学数学探究性学习的思考与实践［J］.中国电化教育，2011（6）：95-98.

［4］ 史宁中.基本概念与运算法则——小学数学教学中的核心问题［M］.北京：高等教育出版社，2013：1-3.