在综合与实践中发展学生的数学素养——以 “探寻神奇的幻方”为例

江西省九江市同文中学 魏立珺

北京师范大学 阮珂怡

数学素养的培育不仅仅是基础知识与基本技能的积累，更重要的是引导学生在教师组织的实践活动中，学会用数学眼光观察现实世界，用数学思维思考现实世界，用数学语言表达世界。在基于真实情境的学习中获取知识、锻炼思维、提升能力、体验成功，这和“综合与实践”领域的教学目标 “培养学生综合运用有关的知识与方法解决实际问题，培养学生的问题意识、应用意识和创新意识，积累学生的活动经验，提高学生解决现实问题的能力”不谋而合。因此，“综合与实践”是数学教育教学中沟通知识学习和实践应用的桥梁，是实现核心素养培育目标的极佳载体。本文以北师大版第一册 “综合与实践课”“探寻神奇的幻方”为例，就如何在课堂教学中培养学生的数学素养分享一些收获与体会。

一、合理选题，情境激趣，用数学眼光发现问题

在明确 “综合与实践”主题内容这一环节，教师不仅要根据学生的经验背景选择教学素材，保证教学内容符合学生当前的知识基础与认知水平，还要兼顾学生的兴趣爱好，激发学生参与教学活动的积极性。在明确“综合与实践”主题内容之后，教师在教学实践中可以创设多种问题、故事、活动的实践情境，找到教学内容的切入点，引导学生进入情境内容，用数学眼光观察问题，激发学生学习数学的兴趣，让学生产生一种强烈的求知欲，给学生创造自主探索的空间，让学生在探索中体会成功的喜悦和成就感，从而增强自信心，培养学生的数学学科能力和素养。

“探寻神奇的幻方”是北师大版七年级上册数学教材“综合与实践”部分的第一个课题。一方面，相较于传统教学，综合实践活动对学生而言是新颖的，可以激发学生的求知欲，而且学生对 “幻方”也有一定的了解；另一方面，学生已经学习了 “有理数及其运算”与 “整式及其加减”，对于 “图形的对称性”也有初步认识，具备了一定的数学探究经验。因此，笔者选定了 “幻方”这一实践主题。

【教学片断一】

师：同学们好！我们中华民族拥有上下五千多年的文明史，在这个历史长河中，我们的祖先在数学领域有许多神奇的发现。今天我们首先通过一个小视频（介绍洛书），带领大家穿越历史，一起回到两千多年前，探究数学的奥秘吧！

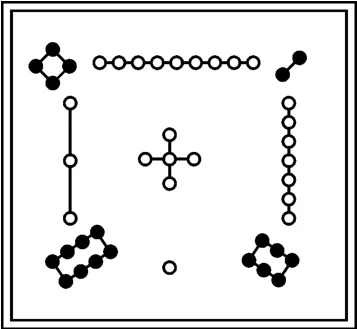
图1

师：请同学们仔细观察下，如果把这个洛书上的图案分成九块，你发现了什么？

生：我发现这些图案可以看成是数字。

师：嗯，这些圈圈点点可以看成我们熟悉的数字，分别对应？

生：4 9 2，3 5 7，8 1 6。

师：好，那请同学们观察这九个数，你能发现哪些相等的数量关系？每行、每列、每条对角线上的三个数之和分别是多少？

生：都是15。

师：好，那像这样一个3行3列的正方形方格中，每一横行、每一竖列和对角线上的数字和都相等，这样的数字方阵称为 “三阶幻方”，其中这个数字和称为 “幻和”……

师：我国对于 “幻方”的记载最早出现于公元前500年，而国外在公元130年，希腊人才第一次提起幻方，因此我国拥有幻方的发明权。古往今来，不少数学家对幻方进行了深入研究，我们为祖先的成就感到自豪的同时，更应该继承与发扬先辈们追求真理、持续探索的科学精神。本节课我们也来研究幻方，并重点研究三阶幻方。

在这部分教学中，笔者先以 “洛书”为引，向学生介绍了幻方的背景知识，激发学生对幻方的研究兴趣，从而引入课题。接着，笔者引导学生观察洛书，发现其中的数学问题，引出 “三阶幻方”的概念。在此基础上，笔者还设置了4×4方格、5×5方格，引导学生计算与发现幻方的共性规律：“每一横行、每一竖列和对角线上的数字和都相等”，进而归纳总结出 “阶幻方”的一般性定义。最后通过告诉同学们本节课重点——研究三阶幻方，引入本节课的主要内容，开启三阶幻方性质和构造方法的探究之旅。在教学过程中，学生学习的积极性与参与度较高，用幻方的文化背景作为课堂引入，不仅可以帮助学生了解数学文化，坚定民族自信，提高审美情趣，也可以激发学生的求知欲望与探究热情，从被动学习转向自主探究，在发现问题、探索规律的过程中欣赏数学之美。

二、设问质疑，合作学习，用数学思维分析问题

数学是一门动态发展的科学，是一门以问题为驱动、不断探索并发展的学科，“综合与实践”是从现实背景出发，以问题为载体、以学生为中心开展的活动课程，符合数学学科的本质特征。在综合与实践教学中，教师要引导学生围绕核心问题的解决展开学习过程，通过自主参与、实践探究、合作交流等方式进行学习，将数学知识与其他学科或日常生活实际建立起紧密联系，鼓励学生从情境中发现、提出、分析、解决问题，亲历思考、试误、反思、调整的全过程，积累综合运用知识、技能、方法的数学活动经验，发展数学思维与数学素养。

【教学片段二】

师：请同学们一起玩个填数游戏，请同学们六人为一小组合作：将1～9九个自然数填入下图的九个方格里，使每行、每列、每条对角线上的三个数的和都相等。请准备好的小组派代表展示在黑板上。（教师进入小组引导）。

生：小组展开热烈讨论，交流做法和想法。

对于该部分教学，笔者引导学生开展小组合作来填写三阶幻方，目的是以问题为驱动，让学生经历解决问题的初步实践，推动实现素养导向的教学目标。基于问题解决的实践经历是学生学习过程中必不可少的活动，学生在探索开放性、挑战性问题的过程中，对于真实情境中的背景知识进行综合分析、推理，将不同领域的知识之间建立联系，产生富有创造性的想法。同时，学生在问题驱动的学习过程中，也能体验发现问题的喜悦、迷茫和困惑，进一步激发探究与交流的热情。

【教学片段三】

教师集中展示已经完成的成果，让学生检查验证，并将正确案例供大家参考研究。请学生从正确的案例中发现规律并进行提炼和说明。

生1：发现“5”应该填写在最中间位置。

生2：角格上都是偶数，边格上都是奇数。

生3：有 “成对的数”：4和6，9和1，2和8，7和3。

生4：可以将洛书那组数进行旋转得到其他组数据。

师：基于以上的交流成果，或者你们小组的研讨，你还能就以上的规律或结论给出怎样合理的解释？

生1：设三阶幻方中的数字分别为a，b，c，d，e，f，g，h，i，则（a＋b＋c＋d＋e＋f＋g＋h＋i）＋3e＝60，45＋3e＝60，解得e＝5。

生2：因为奇数奇数偶数，奇数偶数奇数，偶数偶数偶数，如果 “5”不在中间位置将无法满足题意。当把“5”填入中间格时，如果4个角上填奇数，则其他4格填偶数，我们可以看到第一行、第三行、第一列、第三列的和都得偶数，而根据题目所求，3个数之和为15，15是奇数，所以与题意不符。如果4个角上填1对奇数1对偶数，则剩下的4个格中也应该为1对奇数1对偶数，此时第一行、第三行的和都为偶数，同样与题意不符。如果4个角上都填偶数，剩下的4个格填奇数则符合题意。

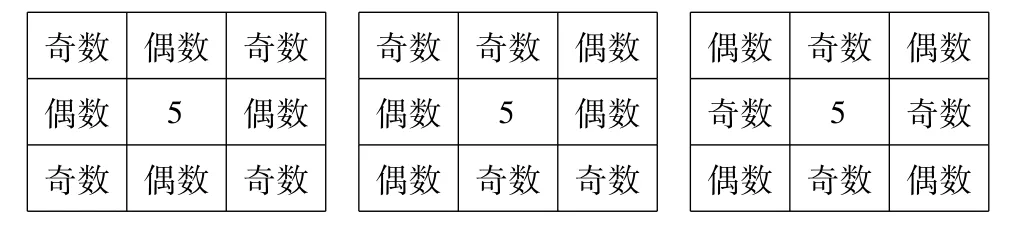
图2

该部分教学，笔者先将学生的案例全部展示出来，要求学生从正确的案例中发现规律、提取经验，充分发挥学生在合作问题解决中的主体作用。学生小组之间相互阐述观点，集思广益，进一步理解三阶幻方的填写方法，在动手操作中体验和发现三阶幻方的对称性特征，明晰数字5处于幻方最中间的原因。同时，笔者也鼓励学生积极发表不同见解，肯定学生的正确想法，并鼓励学生对于已经获得的结论进行质疑与验证，从不同角度思考并探寻新的解题策略。在轻松愉快的课堂氛围中，学生运用数学符号语言进行交流与表达，体会 “从特殊到一般”的数学思想方法，感悟数学探究的乐趣，增强应用意识与创新意识。在引导学生成功探索的基础上，笔者深切体会到 “授之以渔”的重要性，正如钱伟长先生所言：“教师的教主要不是把知识教给学生，而是把处理知识的能力教给学生。”

三、反思提炼，拓展创新，用数学的语言表达问题

数学素养的发展有一个循序渐进的过程，初中是基础教育的重要阶段，在学生发展中起着承上启下的作用，初中教学对于学生数学素养的培育具有重要意义。因此，教师在教学活动中应结合数学学科本质，让学生理解数学概念，把握数学思想，感悟数学思维，追求数学精神，注重真实情境的创设，以问题解决为导向，为学生提供 “从做中学”的机会，要求学生打破思维定式，综合运用各种知识和技能进行探究学习，引导学生开展自主探究与合作来解决现实情境中的问题，为学生创造解决自主问题的空间，使学生成为知识建构的主体，以落实发展学生数学素养的教育目标。

【教学片段四】

师：在下列方格中，从1～9中选择合适的数填写，使横行、竖列及两条对角线上三个数的和都相等。

生：答案不唯一，可以沿着对角线对称。

师：如果我再给你一个数呢？已知这样的三个数呢？写出来的是唯一的幻方吗？

生：唯一的。从上往下，从左往右分别填：7、9、1、4、3、8。

师：小结，整理所获。

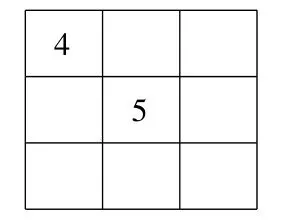
图3

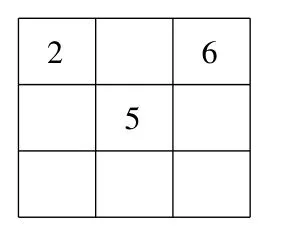
图4

教师提示：（1）知道了什么是幻方；（2）弄清了三阶幻方的本质；（3）学会了构造三阶幻方。

生：经过小组讨论，很快形成思路，即第一步确定“中心数”，第二步配对，第三步分析奇偶性。教师追问“中心数”如何确定，学生加以补充，最终形成五步法：①计算九数之和；②计算幻和（÷3）；③确定 “中心数”（÷3÷3）；④配对；⑤定奇偶。

师：最少需要已知几个数字，使得我们可以确定幻方中的其他数字呢？

师：以小组为单位，撰写关于 “幻方”的研究报告。

成果要求：①尝试解决问题；②需要利用代数式、方程等知识；③以小组为单位分工合作，手写或用软件等撰写研究报告；④对于小组提出的个性化研究问题，可以在报告中阐述研究思路、研究过程与研究结论（选做作业）。

此部分教学，首先，通过运用所学知识解决填数习题，检验学生的研究成果、巩固学生的研究方法，让学生对构造唯一的三阶幻方所需条件有了初步的思考，也给学生创设遇到困难返回案例进行规律再研究的机会。其次，让学生思考本节课所获，就是要学生摒弃小学时对幻方的机械记忆，在了解幻方实质的基础上，形成自己对三阶幻方性质的认识及构造三阶幻方的方法，培养学生归纳总结创新能力。最后，撰写关于 “幻方”的研究性报告，使得学生课后要对 “幻方”进行更深入的研究，这一任务对学生 “用字母表示数”的应用能力也有着更高要求，在撰写中同学们会遇到各种困难和不理解，这就要求教师教授综合与实践课程时，除了安排好课前和课上的内容，更不能忽视课后对学生的引导和帮助。这节课到此落下帷幕，但课后我们的探索还在继续。荷兰数学家弗赖登塔尔认为，“数学学习是一种活动，这种活动与游泳、骑自行车一样，不经过亲身体验，仅仅从书中靠听讲或观察他人的演示是学不到的”。在真实情境中开展综合与实践活动已成为今后数学教学的趋势，其意义不仅在于有效激发学生的数学学习兴趣，还在于让学生在自主探究过程中加深对数学知识的理解，摒弃机械记忆与思维定式，学会知识的迁移与综合运用，进而提升问题解决能力。因此，教师应引导学生关注现实生活，尝试用数学的眼光发现并提出问题，用数学方法思考并解决问题，让数学教学过程脱离抽象符号与理论的桎梏，引导学生从 “做”中学，在亲身实践中体会数学知识的价值与数学文化的魅力，激发数学学习兴趣，在现实问题解决过程中感悟数学之美。

发展数学素养的方式有很多，以上是笔者在教学实践中的几点收获与体会。随着教育理念的不断更新，数学教学经历了从 “双基”到 “四基”，到现在的核心素养，而不管理念如何变化，培养学生的思维能力，教会学生思考，这是永远不会变的，抓住这一核心，并不断提高教师自身的数学素养，吃透教材，充分收集并利用各种教材资源，将自己的核心素养理念贯穿于教学策略中，相信在这样的数学教学中，学生的数学素养一定会得到发展与提高。