增强问题情境体验 深化建模素养形成——以飞镖投掷游戏中的概率问题为例

北京教育学院 陈鹏举 伍春兰

发展数学建模素养的教学，不仅是将数学知识应用到实践中去，更重要的是让学生经历建模过程并从中提炼出新知识，这也是培养其他核心素养的重要手段。生活中有丰富的概率类问题情境，当学生具有一定的概率知识经验之后，让他们经历由实际问题到概率模型的建模过程，是促进学生深刻理解概率理论，形成概率模型解决实际问题的意识和方法的重要途径。下面以真实的飞镖投掷游戏为背景，阐释引导学生经历完整的数学模型的过程。

一、教学背景分析

（一）教学内容分析

概率论起源于博弈理论，是应用数学工具分析博弈问题而逐步形成的相对独立的学科，因此，概率问题与生活中的博弈问题有着千丝万缕的联系，很多现实中的随机问题都可以通过数学建模过程得到其概率。与传统的博弈论相比，现代概率论基于集合论和测度理论，形成了更加严密、准确的理论体系。高中阶段的概率学习将事件之间的关系转化为集合运算，将随机事件抽象为随机变量，用丰富的概率分布模型解释随机现象。因此，引导学生抽取真实情境中的随机变量建立模型关系，是培养学生概率领域数学抽象、逻辑推理及数学建模等核心素养的重要途径。

（二）学情分析

学生在小学阶段已经认识到事件的 “可能性”，能够通过比例关系计算和比较可能性的大小，在初中阶段学习了简单事件的概率，能够通过列举法计算机会的大小，也对频率估计概率有初步认识，但是对事件的概率仅停留在运算层次，并没有对事件及其关系进行深刻剖析。高中阶段引入样本空间、随机变量及其分布来刻画随机现象，这种抽象的表示和关系刻画对学生构成较大的挑战。

据课堂观察及作业分析，学生能够用随机变量及其分布列来表示简单的随机事件结果，但是对于表示较为复杂的事件和分析变量的复杂关系均存在较大困难；学生较为熟悉离散型随机变量及其概率运算，以古典概型为例，他们能够理解通过可能性的样本点的比例关系计算概率的过程，但在将此模型迁移到其他概率模型的过程中仍存在困难。此外，学生容易把生活中的 “可能性”“独立性”等措辞和概率理论方面的概念混淆，针对实践中问题的建模难以明确问题的目标或方向。

（三）学习目标

（1）在飞镖投掷游戏过程中发现真实情境的实际问题，抽象情境中的关键变量，明确提出并概括适合探究的数学问题，经历数学抽象的过程。

（2）经历建立概率模型解决数学问题的完整过程，体验逻辑推理在数学建模的应用，形成探索新事物中概率模型的方法和策略。

（3）在体验游戏的过程中感受游戏的趣味性，在建立模型和验证模型中经历猜想、质疑、验证及完善的科学精神，通过模型反馈感受数学模型的应用价值，感受数学模型的简洁美与抽象美。

（四）学习重点、难点

重点：发现和提出数学问题，围绕关键问题建立数学模型。

难点：概率模型的建立、校验和逐步完善。

二、活动设计与实施

（一）体验真实情境，发现现实问题

活动1：背景呈现，发散思维

情境素材：星期天老师带孩子去游乐园玩耍，路过一游戏摊位时发现一个游戏：游客花1元租1个飞镖，站在垂直地面放置的纸板3米之外投掷，如果飞镖扎在纸板上的五角星上，店主返还游客2元，否则不返还。纸板如图1所示。老师总共租了10个飞镖，大家猜一猜老师赚了还是赔了，为什么？

图1 垂直放置的纸板

学生1：我觉得离这么近，五角星分布又这么密，大概率应该全中，减去10元成本，总共赚了10元。

学生2：我认为老师应该赚不了10元，因为有可能投不中，如果没有投中，对应的就是赔了1元，如果投中，才算赚了1元。关键在于投中五角星的概率，而老师的飞镖技术决定了命中概率，相信老师会赚钱的。

【设计意图】通过展现真实的游戏情境，引发学生思考和讨论的兴趣。教师让学生基于自身的经验先进行猜想，为后面的体验活动的结果冲突做铺垫。同时鼓励学生从感性思考到理性思维转化，比如：盈利额＝2×投中次数－购买成本；投中次数＝投中概率×投掷次数；。

活动2：亲自体验，提出设想

教师提供游戏纸板和游戏代币，按前述规则让学生模拟投掷活动并记录。每名学生租10个飞镖，18名学生共投掷180次，投掷结果见图2所示。

图2 18名学生共投掷180次结果

继而教师引导学生思考并讨论（见表1）。

表1 思考并讨论的问题

【设计意图】只有亲身体验游戏，才能感觉到投掷过程中涉及的诸多变量，以及复杂事件背后的变量之间的关系，这是学生后期建立概率模型的关键。

（二）抽象情境变量，逐步建立模型

活动3：抽取变量，聚焦问题

教师引导学生以分组的形式提炼并聚焦到三个核心数学问题（见表2、表3及表4）。

表2 问题1的假设及数学模型（建模过程略）

表3 问题2的假设及数学模型（建模过程略）

表4 问题3的假设及数学模型（建模过程略）

活动4：提出假设，建立模型

根据上述提出的数学问题，教师引导学生对题干中的关键信息进行提取，分析题干中的关键变量及其关系，结合实际投掷过程提出模型成立的假设条件，逐步建立数学模型解决问题（见表2、表3及表4）。

活动5：回应情境，拓展思维

老师在真实游戏中，总共只投中1次，这个结果和我们建立的模型一致吗？结合活动2中的游戏体验及结果，你认为我们建立的模型2是否合适？如果合适，说明理由；如果不合适，你还有哪些改进建议？

学生：老师在游戏中赔了8元，比建模结果赔得还要多，但是作为个案没有一定的代表性。本班学生共投掷180次，脱靶5次，175次投中纸板中仅有35次命中。平均每位学生的盈利额为，与模型中平均亏6．24元差不多。模型符合真实的投掷预期。

【设计意图】活动3、活动4及活动5，让学生经历完整的数学建模的全过程。

（三）总结建模路径，夯实核心素养

活动6：反思与梳理

教师引导学生回顾学习过程，形成建模过程流程（图3）。

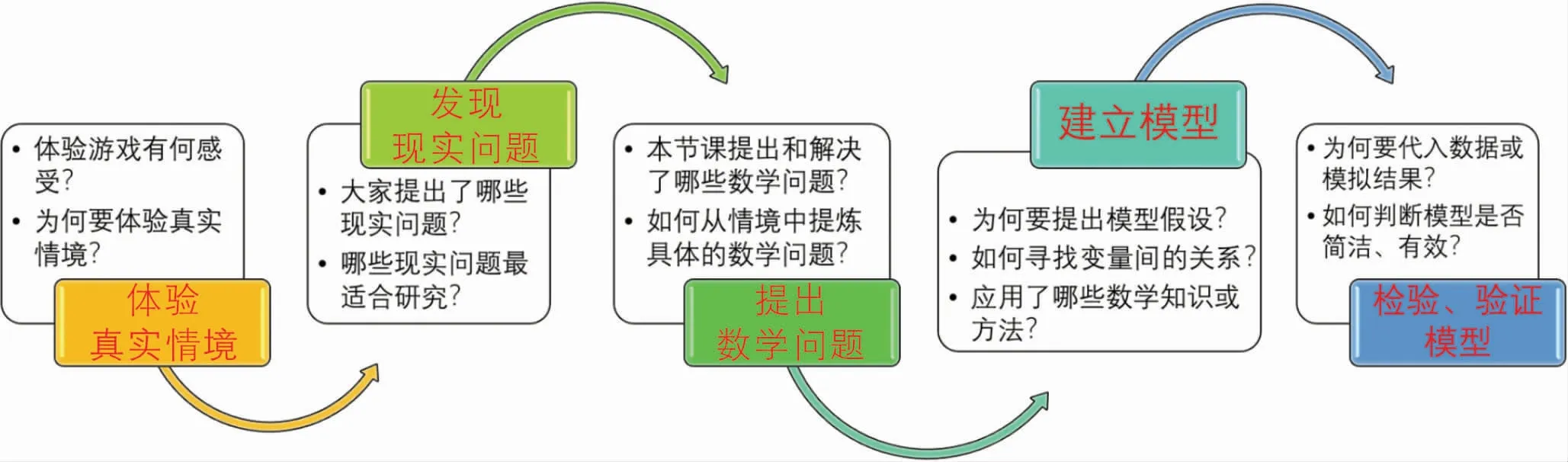
图3 建模过程流程

三、教学反思及建议

结合本节课的设计与实施，提出以下四个方面的教学建议。

第一，重视真实情境创设，建立现实世界联系。

真实情境的创设不仅是为了引发学生的学习兴趣，更重要的是只有真实的情境才能作为真问题的土壤。荷兰教育家弗兰登塔尔提出数学化的思想，他认为学生学习的本质就是把现实世界问题数学化的过程，只有让学生体验到现实世界问题和数学世界问题的联系，才能促进学生有意义地思考。

在日常教学实践中，往往很多情境仅仅是为了引出数学概念，在之后的教学中便弃之如敝屣；为了加快课堂节奏，许多教师会特意把情境的真实性隐去，或者去掉大量真实性信息后，仅仅提供给学生只涵盖数学信息的 “干货”，这样的情境与应用题或考试题无异，不仅学生读之无味，也限制了学生自主思考和拓展思维的空间。

因此，情境创设需要教师既要保障情境与课堂的贴切性，又要维护情境自身的真实性，让情境保持一定的新鲜感，才能促进学生对数学内容进一步思考。

第二，加强学生情境体验，激发问题发现和提出。

情境作为教学中重要的活动素材，教师一般会根据课堂需要让学生熟悉情境。让学生阅读情境是一种常见的方法，学生能够结合数学知识和经验提炼情境中的信息和要素，进而提出自己的观点或问题；但对于很多学生而言，亲自感受和体验更能给他们带来强烈的感官刺激和精神激发。

此外，学生的情境体验是学生熟悉情境中的变量，以及结合自身感受发现提出问题的直接刺激。新课程改革鼓励学生发现问题，但在很多教学中问题往往是教师给出的，缺少刺激学生主动发现问题的过程，而情境体验的过程恰好就是刺激学生自主思考的过程。

第三，以情境问题为引领，逐步完善模型。

无论是数学建模还是数学探究，总是围绕值得探究的问题开展。特别是在数学建模过程中，情境中蕴含的核心问题就是建模的指针，我们必须把明确的、适当的、关键的问题在课堂上让学生提出来。因此，从现实问题入手，让学生广泛提出自己关心的问题，可以形成问题组或问题库，这不仅是一节数学建模课的问题来源，也是学生后续发现新课题或完善模型的来源。

从现实问题到数学问题需要学生进行思考和提炼，充分提升学生抽象概括的能力，让学生用数学的语言表达问题，才能形成数学建模的目标。数学问题是现实问题的遴选、聚焦、抽象和概括，应该鼓励学生大胆地提出问题并精雕细琢地刻画问题，数学问题提出的本身就为数学建模指定了方向。

数学模型的建立显然也是围绕问题逐步展开的，在数学建模的过程中，我们不能希冀学生直接能够得到结果和答案，而是要鼓励学生用自己的思维思考问题，可以从简单到复杂，也可以从特殊到一般，只要学生能够用自己的方法尝试解决问题，我们便认为他在建模的过程中有所进步。

第四，重视情境回馈，体现建模价值

数学模型的价值重在对现实问题的反馈，模型能否经得起现实的检验是学生是否认可建模的关键。因此，在建立模型后，学生期盼将模型回馈于情境中的现实问题或者用模型预测结果。

回馈情境使课堂始于情境创设，终于问题解决，形成问题发现、提出、分析、解决的闭环，这是落实数学建模核心素养的要旨。无论数学模型简单还是复杂，我们都应该尝试将真实的数据代入模型以检验模型的有效性或可靠性，这既是调整模型或完善模型的依据，也是建模数学价值的体现。只有经得起实践检验的数学模型才会被学生认可，数学建模的过程和价值也才会被学生接纳。