立足问题情境 引导深度学习
——以概率统计首轮复习课为例
2023-12-05中国人民大学附属中学通州校区鞠宏伟
中国人民大学附属中学通州校区 鞠宏伟
北京教育学院 伍春兰
概率统计,在《普通高中数学课程标准(2017年版2020年修订)》“学业质量”和 “数据分析”素养上,有明确的由低到高的三级水平刻画,其中第三级水平描述见表1。

表1 概率统计的“学业质量”和“数据分析”素养第三级水平描述
近几年的高考,概率统计部分突出了开放型应用问题的考查。以上述 “学业质量”和 “数据分析”素养第三级的相关要求为依据,结合学生开放型问题缺乏分析和解决的学习体验,在概率统计的首轮复习课,创设了学生知识竞赛的开放情境。
一、教学背景分析
(一)内容及学情分析
概率与统计,是《普通高中数学课程标准(2017年版2020年修订)》必修课程和选择性必修课程的主题之一。学生通过两部分课程的学习,初步掌握了概率统计的相关学习内容(见图1),但是对一些概念的理解还比较肤浅,面对具体问题特别是开放型问题情境,判断、归纳、应用的综合能力不足。

图1 “概率与统计”必修课程和选择性必修课程知识结构
高三学生具有一定的阅读、观察基础,具备一定的合作交流、自主探究能力,对于有趣的问题情境存在好奇心和求知欲,但是由于受数学阅读能力和生活经验所限,很多学生认为概率统计的综合题目比较困难。
为了更好地了解学生概率统计的学习困难,问卷调查了某校高三共计96名学生,题目为不定项选择题。针对各类困难,又随机访谈了若干名学生,得到了一些真实想法。调查结果见表2。
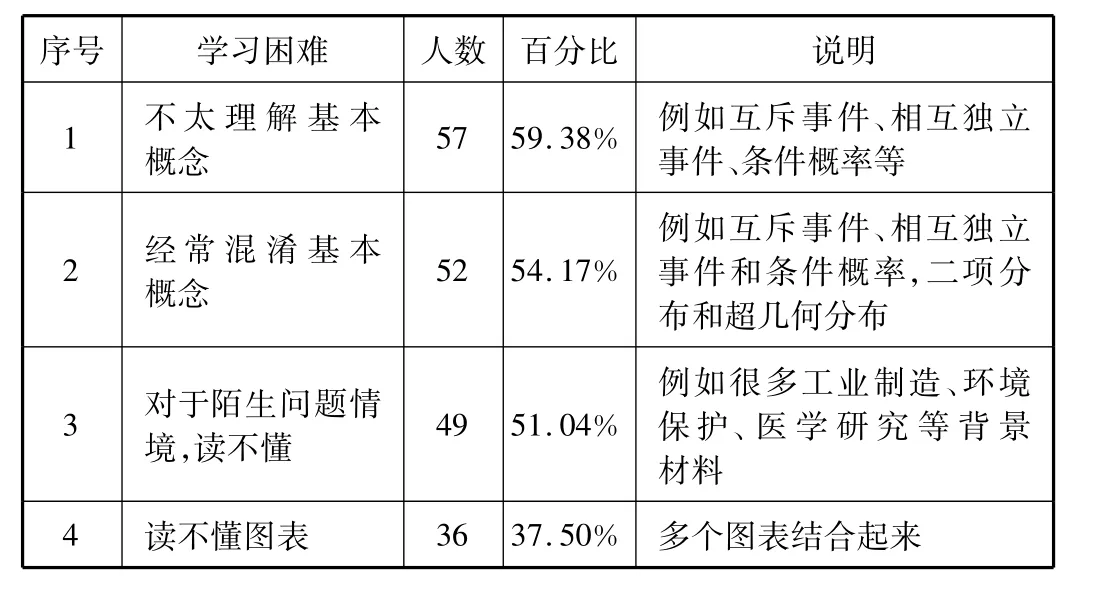
表2 学生概率统计的学习困难统计
在概率统计的首轮复习课,通过团体赛 “决策问题”,引导学生分析解决问题,既强化了学生对概率、期望和方差等基本概念和基本思想的理解与应用,又梳理知识结构完成思维的纵深发展。
(二)教学目标
(1)通过问题情境进行 “决策”,经历用概率统计量描述、分析、解决实际问题的学习体验。
(2)深化对概率、期望和方差等基本概念的理解和应用,从定量和理性的层次上更深入地内化核心概念,实现知识的整合和思维的螺旋式进阶。
(3)体会数学的应用价值,促进概率统计单元的深度学习,培养数据分析、逻辑推理等数学核心素养。
(三)教学重难点
重点:通过问题情境进行分析与探究,做出决策,深刻理解概率、期望和方差等基本概念。
难点:如何理论联系实际,在实际问题中运用恰当的概率统计量分析解决问题。
二、教学过程
(一)创设情境,提出问题
教学背景:校学生会文学社在语文组教师的大力支持下,拟举办 “诗传古韵,词润芳华”的古诗词挑战赛。比赛拟设定预赛、初赛和决赛三个阶段。预赛是客观题,按照积分通过者即可参加后面的比赛。初赛是团体赛,决赛是个人闯关赛,考试形式都是主观题。
初赛赛制拟定如下:以班级为单位择优(预赛成绩)组队,团队的参赛人数需为偶数,且不少于16人。为了避免答题先后的干扰,当一个班级团队全体参赛者都答题完毕后,电脑会依次显示各人的答题是否正确,并按比赛规则裁定该班级团队是否挑战成功。学生会负责人初步拟定了团体赛的两种方式,供每个班自主选择其中之一参赛,但是又不确定两种赛制的制定是否科学合理,是否具有实际可行性,带着这样的问题寻求同学们的帮助:
方式一:将班级团队选派的2n个人平均分成n组,每组2人。电脑随机分配给同一组两个人一道相同的试题,两人同时独立答题,若这两人中都回答正确,则该小组闯关成功。若这n个小组有一半以上闯关成功,则该班级团队挑战成功。
方式二:将班级团队选派的2n个人平均分成2组,每组n人。电脑随机分配给同一组n个人一道相同的试题,各人同时独立答题,若这n个人只要有一半以上回答正确,则该小组闯关成功。且这两个小组必须都闯关成功,则该班级团队挑战成功。
面对以上问题,学生有不同的认识,经过分析得到一些初步的结论。
学生1:这个问题的目的是运用概率统计思想进行决策,从能解决问题的所有方法中,选出最优的方法来。现在我们的主要问题是确定选优原则。
学生2:我认为既然问题比较开放,则可以分析两种赛制的区别,从不同角度比较,比如可以用概率的大小来决定。
学生3:我认为也可以通过分析两种赛制对应的离散型随机变量的期望和方差的大小来决定。
学生4:概率和人数都是不确定的怎么办呢?不确定的条件太多了。但是我可以确定根据问题的描述,“先答题,后出分”“两人同时独立答题”,可见各个同学答题之前是 “相互独立事件”,每组多名同学之间就是“独立重复事件”。
学生5:我觉得通过问题建立理想化数学模型,在团体初赛中,由于每位参赛的同学经过预赛相同题目的选拔,优胜者才有资格参加团体赛。可以假设参赛者水平相当,因此可以设试题回答正确的概率均为常数p(0<p<1)。
设计意图:通过真实问题情境,运用开放型问题导入课堂,体现数学的应用价值,增强学生的探究欲望,形成积极的内在学习动机。从两个不同赛制方式中归纳、概括出问题特征,提升分析、解决问题的意识和能力。
(二)分析情境,解决问题
学生6:我的思路是依托数学期望做决策
对于方式一:设X表示每组2人中回答正确的人数,X为的可能取值为0,1,2,
X的分布列见表3。

表3
且每班参赛人数不少于16人,总的数学期望一定有Eξ≥8p
学生7:我的思路也是依托数学期望做决策,但是我觉得需要按照n分类:
则n挑战成功,这n小组有一半以上闯关成功,
n偶数时:
n为奇数时:
对于方式二:设Y示每组n中回答正确的人数,Y的可能取值为0,1,2…n,
Y~B(n,p)
Y的分布列见表4。

表4
学生8:我认为利用数学期望的大小表示随机变量平均取值的大小,在这个问题中可以初步体现两种方式的差异,但是并不能明确表示是否 “挑战成功”,研究的结论差异也不明显。我的思路是,在此基础上利用方差的大小作比较,因为方差可以衡量随机变量或一组数据时离散程度的度量,用方差研究偏离程度有何稳定性,本题可以利用是否 “挑战成功”利用0-1分布表示。
ξi(i=1,2)表示挑战结果,其中0表示挑战失败,1表示挑战成功。
对于方式一,每组的2个人的挑战结果,ξi服从0-1分布,方式一的ξ1分布列见表5。
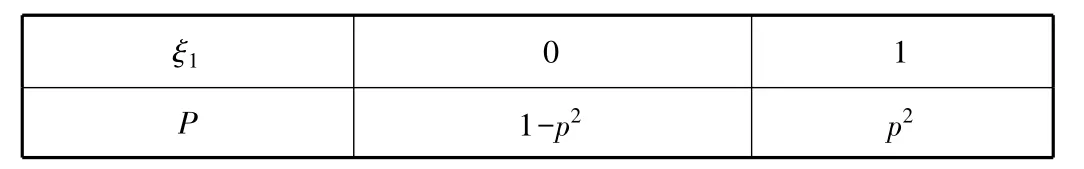
表5
学生9:方式一是若这n个小组有一半以上闯关成功,则该班级团队挑战成功。那么如何用方差表示呢?同样方式二的ξ2分布列如何解决呢?我认为可以依托概率的大小做决策,假设参赛者回答正确的概率均为常数p(0<p<1)。
则选择方式一每组2人都挑战成功P(X=2)=p2(见表6);

表6
n为偶数时:
n为奇数时:
选择方式二:设Y表示每组n人中回答正确的人数,Y为的可能取值为0,1,2…n,Y~B(n,p)。
n为偶数时:
n为奇数时:
学生10:我认为方式二可以应用古典概型的理论和极限的思想,。
设计意图:结合实际的决策问题,对比数学期望、方差和数学概率三种决策方案的可行性和问题,明确了应用概率统计知识进行决策问题选优的原则。
(三)深化情境,拓展问题
学生会负责人:我预设的两种赛制方式的目标是“获胜”,经过同学们上述分析,发现应用期望和方差计算不太适合,应用概率作为决策标准比较直观适用,但是求解过程又比较复杂。请同学们帮我修改一下比赛方式!
学生10:我认为为了提高可行性,可以修改如下(方式三和方式四)。
方式三:将班级团队选派的2n个人平均分成n组,每组2人。电脑随机分配给同一组两个人一道相同的试题,两人同时独立答题,若这两人中至少有一人回答正确,则该小组闯关成功。若这n个小组都闯关成功,则该班级团队挑战成功。
方式四:将班级团队选派的2n个人平均分成2组,每组n人。电脑随机分配给同一组n个人一道相同的试题,各人同时独立答题,若这n个人都回答正确,则该小组闯关成功。且这两个小组必须都闯关成功,则该班级团队挑战成功。
学生11:我认为新的方案比较可行,其中问题明确,挑战成功的可能性更大,即应用概率大小进行,设选择方式三、四的班级团队挑战成功的概率分别为P1,P2。假设参赛者回答正确的概率均为常数p(0<p<1)。
当选择方式三时:
因为两人都回答错误的概率为1-p2,则两人中至少有一人回答正确的概率为1-(1-p)2。则P1=[1-(1-p)2]n=[1-(1-2p+p2)]n=(2p-p2)n=pn(2-p)n。
当选择方式四时:
因为一个小组闯关成功的概率为pn,则一个小组闯关不成功的概率为1-pn,则P2=1-(1-pn)2=1-(1-2pn+p2n)=2pn-p2n=pn(2-pn)。
学生11:两种方式对应概率的求法都比较简单,可是最后怎么比较大小呢?期待同学们的帮助。
学生12:可以用作差比较法啊!
P1-P2=pn(2-p)n-pn(2-pn)=pn[(2-p)n+pn-2]。
由0<p<1,pn>0,
设f(n)=(2-p)n+pn-2,
则有f(n+1)-f(n)=[(2-p)n+1+pn+1-2]-[(2-p)n+pn-2]
=(2-p)n+1+pn+1-(2-p)n-pn=(2-p)n(2-p-1)+pn(p-1)
=(2-p)n(1-p)+pn(p-1)=(2-p)n(1-p)-pn(1-p)
=(1-p)[(2-p)n-pn]
由0<p<1,则1-p>0,2-p>1,所以(2-p)n>1,pn<1,
即f(n+1)-f(n)=(1-p)[(2-p)n-pn]>0。
所以f(n+1)>f(n),即f(n)单调递增。
学生13:我认为为了严谨,需要求出f(2),
又f(2)=(2-p)2+p2-2=2p2-4p+2=2(p2-2p+1)=2(p-1)2>0。
由已知n≥8,则f(n)>0,P1-P2>0,即P1>P2。
学生会负责人:谢谢大家,我明白了!按照这两种方案,若使本班挑战成功的可能性更大,应该选择第三种方式参加比赛,这个比赛既推广了传统文化,又启发每班进行方法选择的数学研究,我感到非常有意义!
设计意图:基于进阶性的问题情境设置,意在围绕数学核心内容,从而搭设一系列由浅入深、由表层知识到知识本源、问题序列的情境,给予学生体会由 “用以致学”到 “学以致用”的机会。
(四)回顾情境,反思问题
师生进一步梳理知识,总结完善知识体系,并形成发现提出问题、分析解决问题的路径(见图2)。

图2 发现提出问题、分析解决问题的路径图
三、教学反思
(一)问题情境要引 “深”到学生世界中
学生作为学习的主体,在数学知识基础、认知基础等方面存在一定差异,构建的问题情境要能让数学知识引起不同层次的学生深度互动,才能不断激发兴趣、激发情感、激活思维,才能使用数学的眼光观察世界成为可能。
(二)问题情境引 “深”到现实的问题中
引导学生对现实生活中客观存在的现象,运用数学知识,有意识地、主动地对其进行解释,实现对现象本质的认识;同时学生学到一定的数学知识后,要有意识地思考在现实生活中应用这个数学知识能解决什么问题,理论联系实际,可以使学生在数学和现实中不断切换,才能使用数学语言表达世界成为可能。
(三)问题情境引 “深”到知识的本源中
学生超越数学知识表层实现对知识本源的理解、达成意义系统的构成是数学深度学习达成的基本特征之一。问题情境设置,一方面需要引导学生不断深刻领悟知识本源的基础上融会贯通;另一方面,需要实现学生对知识的转化、处理、重构,才能对所学知识本质和规律有真正的理解,才能使用数学的思维思考世界成为可能。
