素养导向的基础性作业分层设计策略

北京师范大学 付 强 綦春霞 张 彬

杭州学军中学海创学校 陈智豪

一、作业设计原则

（一）发展学科素养原则

作业要以发展学生核心素养为目的，以巩固所学知识与技能为基础，注重培养学生发现、提出、分析和解决问题的能力、综合实践能力，渗透数学思想方法。作业设计时，要有利于学生积累数学活动经验，着力发展“学科关键能力”，激发学生的 “问题意识”，让学生带着 “问题”做作业，不断促进学生数学思维的发展。要以达到开阔、拓展学生学科视野、思维深度和广度为作业设计质量标准。

（二）依据课标设计原则

作业设计的内容与难度要符合《义务教育数学课程标准（2022年版）》要求，符合中学生的认知水平、年龄特点，注重在具体情境中的应用。

（三）与目标一致性原则

作业设计要依据课堂学习目标，遵循作业与课堂学习目标一致性理念，把课后作业和课堂教学有机结合起来，发挥作业的诊断、巩固、学情分析等功能。从激发学生学习兴趣的角度出发，使得对于不同层次的学生都具有挑战性。杜绝低难度、机械训练、重复性以及惩罚性作业。

（四）学科统筹兼顾原则

各学科作业量要有效统筹，相互兼顾，彼此协调，将全部科目的作业量加在一起，计算学生作业总时长，作业总时长要以教育行政部门规定的时长为依据，作业总量以三分之二的学生在规定时间内完成为宜。

二、作业设计类型

（1）基础类作业，侧重于巩固学生所习得的学科基础知识和基本技能而设计的作业，重点围绕学生对知识进行建构和直接应用课堂习得的基本知识或基本技能解决知识问题情境中的简单问题来设计，以巩固必备知识为主要目的。

（2）综合类作业，侧重于训练学生习得知识与技能过程中所借助的过程与方法而设计的作业，这类作业重点围绕学生如何借助已有知识和新知识，综合运用多种知识技能或方法解决学习探索情境或生产、生活实践情境中的综合性问题来设计，以训练学生学科关键能力为主要目的。

（3）反思类作业，侧重于训练学生建构核心知识体系、领悟掌握学科思想和学科方法、形成正确的观点或观念。一般是通过一些开放性的问题训练学生综合运用知识技能、思想方法、活动经验解决问题或进行阐释，注重训练学科思维，拓展学科视野，凸显学科价值而设计的作业，以培育正确的价值观、积淀素养为主要目的。

根据课型、内容的不同，每一节课不一定同时设计三种类型的作业，作业设计的每一种类型中，还可以有动手操作、实验操作、社会调查、案例研究、知识梳理等多种形式。

三、作业设计策略与示例

（一）作业设计策略

在课堂上，教师发展学生核心素养的主要路径有两条，一是以必备知识为载体，让学生经历、体验获得知识的路径与方法；二是在新情境中，让学生运用获得的知识与方法解决新问题。因此，素养导向的作业设计就要以这两条路径为切入点，以必备知识为核心设计问题情境，或学习探索情境，或生产生活实际应用情境，通过任务设置完成作业设计。找到了作业设计的切入点，教师就能设计以提升素养为导向的作业了。

以情境、任务的复杂度作为作业分层的抓手。作业分层包括情境分层与任务分层。

情境分层就是根据复杂程度，把情境分为简单情境、一般情境、复杂情境。其中，简单情境是指表现内容不复杂、呈现形式比较直接、情境隐含知识点比较单一的情境，多为知识问题类情境；一般情境是指表现内容或呈现形式相对简单但信息量相对较大的情境，多为学习探索类情境；复杂情境是指反映的内容层次较多、呈现的形式比较多元，隐含知识点相对较多、需要深入解读的情境，多为生产生活实践情境。

任务分层就是根据任务的复杂程度，将任务分为简单任务和复杂任务。其中，简单任务是指要求学生调动单一的知识或技能就能解决问题的任务；复杂任务是指学生在正确思想观念引领下，综合运用多种知识或技能才能解决问题的任务，或者是在正确的思想观念引领下，在开放性的综合情境中能创造性地解决问题，形成创造性的结果或结论的任务。

因此，作业分层设计要关注以下五个要素。

要素一：作业设计要以巩固、检测、发展学生核心素养为目的。

要素二：作业的基本范式是 “情境＋任务”。

要素三：根据核心素养的发展内涵确定作业类型。

要素四：作业设计要以知识形成路径和应用场景为切入点。

要素五：以情境、任务的复杂度作为作业分层的抓手。

（二）作业设计示例

例1：北师大七年级下册4.1.3“三角形的中线、角平分线”

课标要求：1.理解三角形中线、角平分线的概念；2.了解三角形重心的概念。

本节课的作业依据是课标要求，可设计以下三个类型。

1.基础类作业：学生在理解三角形的中线、角平分线的概念后直接应用，利用三角形中线、角平分线的概念即可解决问题。

示例1．如图1，D，E分别是△ABC的边AC，BC的中点，则下列说法不正确的是（ ）。

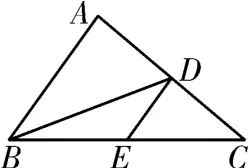
图1

A.DE是△ABC的中线

B.BD是△ABC的中线

C.AD＝DC，BE＝EC

D.DE是△BCD的中线

说明：此作业的设计是以已知△ABC的边AC，BC的中点，辨认关于中线或中点的相关问题为问题情境。学生在理解三角形中线概念的基础上，只要利用三角形中线的知识，在给定的图形中，从不同角度不同方向就可识别三角形中线。

本作业设计的目的是巩固理解三角形的中线概念。

2．综合类作业：在理解三角形中线、角平分线概念的基础上，经历与三角形周长、平行线的性质建立相关联系的过程，综合运用相关知识进行分析、选择恰当的方法解决问题。

示例2．如图2，已知BD是△ABC的中线，AB＝5，BC＝3，△ABD和△BCD的周长的差是（ ）。

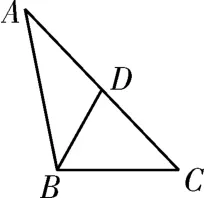
图2

A.2 B.3

C.6 D.不能确定

说明：此作业的设计是以已知△ABC的中线及两边长，求两个三角形周长差为问题情境。学生在理解三角形中线概念的基础上，利用三角形中线知识，综合应用三角形的周长、中线及方程方法，得出求三角形的周长差实质就是边AB与BC的差，从而解决问题。

本作业设计的目的是三角形中线、周长及方程方法等知识的综合应用。

3．反思类作业：综合使用线段中点、三角形中线可转化为线段相等及三角形中线把三角形分成面积相等的两个三角形等转化思想和活动经验，运用转化、类比的数学思想，在学习探索情境中解决问题。

示例3．如图3，在△ABC中，已知D，E，F分别为BC，AD，CE的中点，且S△ABC＝4 cm2，则阴影部分的面积是多少？

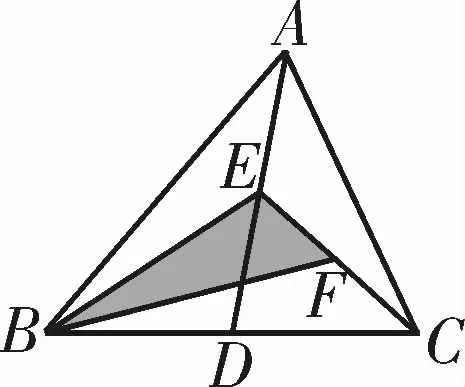
图3

说明：此作业的设计是以已知△ABC各边的中点，求阴影部分的面积为问题情境，利用线段中点、三角形中线可得线段和面积相等的转化思想和活动经验，结合图形特点，通过类比思想方法、几何直观找出阴影部分面积实质为△ABC的四分之一，解决阴影部分的面积问题。

本作业设计的目的是三角形的中点、中线及面积的相关知识体现出来的转化、类比的思想方法、推理能力的拓展应用。

例2：北师大版九年级上册2．2“用配方法求解一元二次方程”

课标要求：理解配方法，能用配方法解数字系数的一元二次方程。

本节课的作业依据是课标要求，可设计以下三个类型。

1．基础类作业：学生在理解配方法的基础上，能利用配方法对一元二次方程进行变形，并能解数字系数的一元二次方程。

示例1．用配方法解方程x2＋8x＋9＝0，变形后的结果正确的是（ ）。

A.（x＋4）2＝－9 B.（x＋4）2＝－7

C.（x＋4）2＝25 D.（x＋4）2＝7

说明：此作业的设计以配方法解方程x2＋8x＋9＝0为问题情境，在理解配方法的意义和基本步骤的基础上，利用所学的知识与技能得到变形后的形式。

本作业设计的目的是巩固理解配方法。

2．综合类作业：将配方法、偶次幂的非负性、平方根等知识建立相关联系，综合运用相关知识进行分析、选择恰当的方法解决问题。

示例2．不论x，y为什么实数，代数式x2＋y2＋2x－4y＋7的值（ ）。

A.总不小于2 B.总不小于7

C.可为任何实数D.可能为负数

说明：此作业的设计以不论x，y为什么实数，代数式x2＋y2＋2x－4y＋7的值为问题情境，综合应用配方法、偶次幂规律相关知识解决问题。

本作业设计的目的是配方法、偶次幂规律相关知识的综合应用。

3．反思类作业：综合运用配方法、偶次幂的非负性等相关知识，通过阅读理解建立活动经验，运用转化、化归的数学思想，在学习探索情境中，运用适当的方法解决问题。

示例3．阅读下面的解答过程，求y2＋4y＋8的最小值。

解：y2＋4y＋8＝y2＋4y＋4＋4＝（y＋2）2＋4≥4，

∵（y＋2）2≥0，即（y＋2）2的最小值为0，

∴y2＋4y＋8的最小值为4．

仿照上面的解答过程，求m2＋m＋4的最小值和4－x2＋2x的最大值。

说明：此作业的设计以一则阅读材料为问题情境，结合材料和所学内容，经过类比、迁移，用配方法对m2＋m＋4和4－x2＋2x进行变形，得到解决问题的途径。

本作业设计的目的是用配方法、偶次幂及最值的相关知识去进行拓展应用。

例3：北师大版八年级上册6．2“中位数与众数”

课标要求：1．经历收集、整理、描述和分析数据的活动，了解数据处理的过程；2．理解中位数和众数的意义，能计算中位数和众数，了解它们是数据集中趋势的描述。

本节课的作业依据是课标要求，可设计以下三个类型。

1．基础类作业：学生在理解中位数、众数的基础上，能求出一组原始数据的中位数和众数，或者以表格形式出现并经过初步整理的数据的中位数和众数，在简单情境中选择合适的量描述数据的集中趋势，能计算中位数和众数。

示例1．某鞋厂调查了商场一个月内不同尺码男鞋的销量，在平均数、中位数、众数等统计量中，该鞋厂最关注的是________。

说明：此作业的设计以商场调查不同尺码男鞋的销量为问题情境，学生在理解平均数、中位数、众数的基础上，利用众数的意义及三者之间的区别与联系就可以选择合适的统计量。

本作业设计的目的是巩固理解平均数、中位数、众数。

2．综合类作业：将中位数、众数和平均数的知识建立相关联系，综合运用数据分析能力解决问题。

示例2．已知一组数据6，x，3，3，5，1的众数是3和5，则这组数据的中位数是________。

说明：此作业的设计以一组数据6，x，3，3，5，1的众数是3和5，求这组数据的中位数为问题情境，综合应用中位数、众数相关知识，先确定x的值，即可求出中位数。

本作业设计的目的是中位数、众数相关知识的综合应用。

3．反思类作业：综合运用平均数、中位数、众数等相关知识，或多种统计图表参与的实际问题情境；通过数据分析观念，基本活动经验，在学习探索情境中，利用分析数据的集中趋势，运用适当的方法解决问题。

示例3．在从小到大排列的五个数x，3，6，8，12中再加入一个数，若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等，则x的值为______。

说明：此作业的设计以从小到大排列的五个数x，3，6，8，12中再加入一个数，利用两组数据的中位数、平均数的关系，求未知数据的值为问题情境，对中位数、平均数的相关信息的分析，通过所学的知识解决问题。

本作业设计的目的是理解两组数据的中位数、平均数的相关知识体现出来的数据分析观念，基本活动经验的拓展应用。

四、结语

充分理解基础性作业分层设计的本质，合理进行推广与拓展，可以使学生跳出题海，真正体会数学学习的本质，达到了事半功倍的效果。因此，在日常教学中，教师们应多关注基础性作业分层设计的规律，力求使教学更加有效。