生长数学视角下的高中数学概念教学案例研究

程玉林 蔡华远

摘 要：概念是高中数学学习的基础。开展有效的高中数学概念教学，能够帮助学生夯实数学基础，有助于他们进一步探索数学知识。生长数学是一种新的教学理念，它在高中数学概念教学中的应用能够帮助学生从概念出发，内化数学知识，提升核心素养。文章解读了生长数学的基本内涵，阐述了生长数学在高中数学概念教学中的应用意义，并具体分析了生长数学视角下高中数学概念教学实施的具体案例。

关键词：高中数学；生长数学；概念教学；案例研究

中图分类号：G427                                文献標识码：A                                       文章编号：2097-1737（2023）30-0020-03

高中数学概念是学生学习数学知识、提升思维和学习能力的重要基础。教师在高中数学概念教学中要明确生长数学对学生成长的重要意义，并在教学实践中积极分析应用的具体方法，促进学生能力的发展。在生长数学视角下，教师要探索高中数学概念教学实施的具体策略。

一、解读生长数学基本内涵

生长数学主要观点包括：数学教学本身就是一种成长；数学教学应为学生的成长助力；数学教学要培植思维生长的种子；实践上要让学生学习具有生长力的数学[1]。生长数学注重在数学教学中发挥知识的生长功能，促进学生的成长。生长数学一方面是从学生角度出发，尊重学生的生长规律，让学生通过知识的学习实现综合素质的全面成长。生长数学能帮助学生发现问题，并通过引导学生观察、思考、分析以及解决问题来培养学生的思考能力，促进学生思维能力的发展。在问题的探究过程中，学生可以通过自主以及合作学习实现学习能力的发展[2]。生长数学是一个完整的学习过程。从学生获取知识到运用知识，这是学生将知识内化的过程，也是学生数学学科核心素养生长的过程。生长数学的另一方面是从数学学科角度出发，将生长数学理念应用于课堂教学中。教师需要秉承生长的理念，在数学课堂上给学生提供机会，让学生对数学问题进行思考和探究，为学生提供开展深度学习的外部环境，助力学生成长。在生长数学理念下，

数学教学的目的在于遵循学生的成长规律，为学生的内生长提供强有力的助力。

二、生长数学在高中数学概念教学中的应用意义

（一）创新数学教学理念

当前，部分教师在紧张的高中数学教学中常常会忽略概念教学的重要性，将更多的时间和精力放在了提升学生的成绩上，这主要是受应试教育理念的影响。在应试教育理念下，高中数学概念教学很难发挥对学生的促进作用，而生长数学在高中数学概念教学中的应用则能够给教师的教学活动带来新的思考。教师需要转变传统的应试理念，创新以“生长”为课堂目标的教学理念。这样教师能够深刻认识到概念教学的重要性，从而构建“生长环境”，探索促进学生生长的具体策略。因此，生长数学在高中数学概念教学中的应用，能够创新数学教学理念，推进生长理念的应用。

（二）深化学生的概念理解

教师在概念教学中通常不会花太多的时间进行深入讲解，这就导致学生对一些概念的理解并不深刻。生长数学在高中数学概念教学中的应用则是鼓励学生通过不同的角度和层次来全面理解相应概念[3]。在生长数学理念下，学生对概念的理解不是通过教师的讲解和演示，而是通过自主学习或者合作探究的形式获得。不同的学生看待问题的角度各不相同，学生在互相交流和沟通中会更全面地思考问题，更深入地理解概念，从而实现全面成长。由此可见，生长数学在高中概念教学中的应用能够深化学生对概念的理解。

（三）推进学生的深度学习

当前，培养学生数学学科核心素养是高中数学教学的核心任务。学生核心素养的形成离不开对数学的深度学习。数学概念是学生探索数学知识体系的基础，也是学生开展深度学习的基础。学生在明确概念的基础上，才能更高效地展开深度学习。生长数学在高中数学概念教学中的应用能让学生在概念的学习中达到思维生长、能力生长、品格生长及素养生长等目标。学生的这些综合素养的生长能够迁移到对数学知识体系的构建中，使学生延续良好的思维和学习方式，对数学知识进行全面深入的探究。生长数学在高中数学概念教学中的应用能为学生的深度学习积聚内在能力，从而推进学生的数学深度学习。

三、生长数学视角下高中数学概念教学案例分析

（一）创设情境，激发学生对概念学习的探索欲

高中数学教师在概念教学中通常是对概念进行逐字逐句的讲解，然后让学生进行课堂练习巩固所学。在这种教学形式下，学生感受不到学习概念的意义，也难以产生探索欲。在生长数学教学理念下，教师要通过创设相应的教学情境，激发学生对概念的探索欲，引导学生主动探索数学概念。以人教A版高中数学必修第一册“二次函数与一元二次方程、不等式”中一元二次不等式的概念教学为例，一元二次不等式的一般形式是ax2+bx+c﹥0或ax2+bx+c﹤0（其中a、b、c均为常数，且a≠0）。为了激发学生主动学习的欲望，教师可以通过情境激活课堂，为学生的学习生长营造良好的氛围。教师可以在课堂上创设以下生活化的问题情境，利用多媒体出示两辆汽车相撞的图片并附带文字说明：“在一个限速40km/h的弯道上，甲车和乙车相向而行，当两位司机意识到可能会相撞时同时刹车，最终还是相撞了。经过事后交警对现场的勘察，甲车的刹车距离超过了12 m，乙车的刹车距离超过了10 m，

甲车的刹车距离S与车速x的关系为：S甲=0.1x+0.01x2，

乙车的刹车距离S与车速x的关系为：S乙=0.05x+

0.005x2，那么这场车祸应该判定为谁的责任？”。然后教师提出问题：“我们知道交通事故发生后，交警的责任就是通过勘察和判断来判定责任方。请同学们思考，如果你是交警，你会怎样依据已知信息判定责

任呢？”

在这样的生活化问题情境中，教师可以构建课堂知识与生活实际的联系，增强课堂知识的趣味性和实用性。学生通过对事例进行深入的分析得出，两辆车同时刹车但是刹车距离却不相同，那么可能会存在超速的现象。接下来，学生要想探索是否存在超速，就需要对一元二次不等式展开深入的探究学习。这样，教师能够利用生活化的问题情境激发学生对一元二次不等式概念的探索欲。

（二）组织学生对特例进行思考，学习归纳概念

教师在生长数学理念的应用中，要引导学生对特例进行思考探究和分析，通过探索研究来归纳数学概念，从而实现学生思维的拓展。以人教A版高中数学必修第二册“随机抽样”的概念教学为例，教师可以组织学生通过探究进行特例的分析对比，然后归纳概念，加深学生对概念的理解。在课堂上，教师可以让学生对随机抽样的概念进行思考和学习：“同学们，步入高中后学习压力越来越大，此时身体健康就显得更加重要。为了更好地了解同学们的健康状况。学校决定抽查一下整个高一年级学生每周的体育锻炼时长。那么今天就请同学们以小组合作的形式来帮忙制订一个随机抽样的具体方案。”

在这样的任务引导下，教师可以让学生以小组合作的形式，共同进行随机抽样概念的探索学习，然后引导各小组展示和交流不同的抽样方案。

小组1：“我们认为考虑到减少调研的工作量和调研数据的准确性，应该排除班级内的相互影响因素，以班级为单位，每个班级应选取班级人数的10%来填写问卷。这样既能减轻工作量，又能保证调研数据的准确性。”

小组2：“我们觉得既然要调查学生的体育锻炼情况，就要考虑到每个班级中的特殊情况，比如：体育特长生。所以我们觉得应该把每个班级中的学生都按照体育能力划分上、中、下三个层次，然后在每个班级的不同层次中抽取学生人数的10%进行调查，这样的随机抽查才更准确。”

......

师：“听了同学们的方案，老师觉得每个小组都有各自的想法。刚才我们制订了这么多随机抽样的方法，请同学们思考一下，到底什么是随机抽样呢？”

生1：“我觉得无论是从整个高一年级中直接选取特定的比例，还是将年级划分为班级再从班级中抽取比例或者再对班级中学生进行细化分层抽取比例，本质都是从抽样的总体中随机抽取一定的样本，样本肯定是总体的子集。所以，我觉得从总体中随机选出子集就叫作随机抽样。”

生2：“我觉得随机抽样应该是划分类别的。从总体中随机选取样本这样的抽样方法是比较简单的，应该叫简单随机抽样。按照某种标准划分层次，然后从每个层次中抽取同比例的样本，应该叫分层随机

抽样。”

......

通过不同学生对随机抽样方案的制订，教师可以组织学生从不同的方案中思考分析共性，从而概括随机抽样的概念。这样的教学方法不仅能够让学生通过思考进行特例的探究和分析，还能帮助学生在对比、归纳和总结中深入掌握概念的内涵，促进学生思维和学习能力的生长。

（三）在概念的实践应用中积淀学生数学素养

高中数学概念教学的生长力主要体现在学生能够运用所学概念来解决生活中的實际问题。在概念教学中，教师要组织学生对数学知识进行实践应用，让学生在概念的实践应用探索中实现数学素养的生长。以人教A版高中数学选择性必修第一册“直线和圆的方程”为例，教师可以引导学生运用圆的标准方程的概念[（x-a）2+（y-b）2=r2]解决实际生活问题，促进学生数学学科核心素养的成长。在课堂上，教师可以引导学生思考：“同学们，我们之前学习了圆的标准方程，

那么通过对圆的标准方程概念的理解，你们觉得它能用来解决生活中的哪些问题呢？”

生1：“我觉得它能解决生活中很多跟圆形、半圆或者拱形相关的问题，比如研究半圆形桥的限高问题。”

生2：“我觉得能够解决农业种植中半圆形的大棚需要搭建多高的问题。”

师：“同学们分析得非常好，接下来我们看一个案例。我们都知道，桥下设有支柱能够提升拱桥的承载力，那么支柱的高度一定要严格按照标准设置，不能太高也不能太低。如果你是这个拱桥的设计师，你会将A2P2的高度设计为多少呢？”

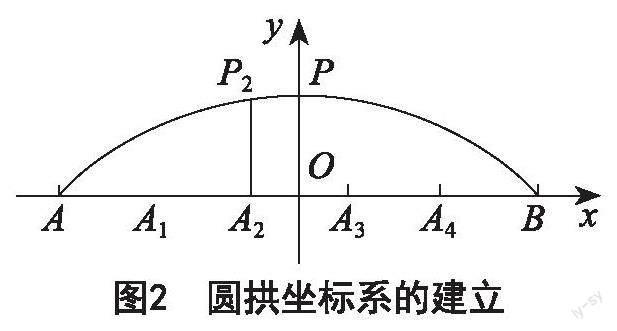
教师利用多媒体展示案例：下图（如图1）是某圆拱桥一孔圆拱的示意图，圆拱跨度AB为20 m，圆拱高OP为4 m，每间隔4 m需要撑一个支柱，求支柱A2P2的高度（精确到0.01 m）。

通过这个与建筑工程紧密相关的实践问题，教师可以引导学生对圆的标准方程进行深入探究思考。通过分析，学生首先需要构建圆拱与圆的标准方程的联系，建立坐标系（如图2），找出圆上的三个坐标点即A（-10，0）、B（10，0）和P（0，4），将其代入圆的标准方程（x-a）2+（y-b）2=r2，最终得出a=0，

b=-10.5，r2=14.52，则圆的标准方程为x2+（y+10.5）2=

14.52。将P2的横坐标x=-2代入，得出纵坐标约为

3.86 m。那么，支柱A2P2的高度应为3.86 m。在对圆的标准方程概念进行实践应用的过程中，学生需要结合图形对问题进行深入的观察、思考、分析、计算以及最终验证。这个探索尝试的过程也是学生数学学科核心素养全面成长的过程。在生长数学视角下，教师可以引导学生对概念进行实践探索，促进学生数学学科核心素养的生长。

四、结束语

总而言之，在新的教学形势下，高中数学教师要深刻地认识到生长数学在概念教学中应用的重要性，深入理解生长数学的内涵，在概念教学中积极探索生长数学推进学生的深度学习以及学科核心素养形成的具体策略。

参考文献

[1] 卜以楼.生长数学：卜以楼初中数学教学主张[M]. 西安：陕西师范大学出版总社，2018.

[2] 郭京港.旨在提升成长型思维的高中数学变式教学设计研究[D].南昌：江西师范大学，2022.

[3] 唐剑，王士喜，黄遵学.基于生长数学理论的高一学生数学错题矫正策略研究[J].中学数学教学，2022（2）：35-38.

基金项目：本文系2022年晋江市基础教育教学改革专项课题“生长数学视角下高中数学概念教学的案例研究”（立项编号：JJ2022-ZX03）的研究成果。

作者简介：程玉林（1986.2-），女，福建晋江人，

任教于福建泉州晋江市陈埭民族中学，一级教师，研究生学历，2021年获得陈埭镇优秀教师称号。

蔡华远（1983.8-），男，福建泉州人，任教于福建泉州第五中学，一级教师，研究生学历，2018年获泉州第五中学优秀教师称号。