高考数学审题五环节
2023-11-25薛晋红
薛晋红


摘要:审题是解题中至关重要的一步,也是解题成功与否的关键所在.审题是根据题目条件,正确阅读理解,提取有效信息,挖掘隐含信息,提炼关键信息,合理构建数学模型.结合高考真题,总结审题“五环节”,借助数学知识,推理运算破解,展示常见审题技巧与解题策略.
關键词:审题;高考;条件;关键;转换
数学审题就是正确弄清题目条件与内涵,这是解题的基础,是能否正确、迅速解题的关键.因而要想有效解决数学问题,关键就是要把好审题关.如果审题掉以轻心,往往会导致数学思维的偏差,致使解题失误或陷入到繁冗的解题中[1].
1 环节一:题设字斟句酌,全面弄清题意
认真细致审题的重要策略就是逐字逐句地仔细分析,特别是一些容易看错、理解错、被忽视或被误解的字、词、句等,要善于“字斟句酌”,弄清题意与内涵实质,为正确数学解题创造条件.
例1 (2022年高考数学上海卷·10)已知等差数列{an}的公差不为零,Sn为其前n项和,若S5=0,则Si(i=1,2,3,……,100)中不同的数值有个.
审题:结合题设,抓住等差数列的背景,理解其中的关键语句“S5=0”,合理建立关系式,确定等差数列的首项与公差之间的关系,结合等差数列的前n项和将所求问题转化为二次函数的相关问题,弄清问题的内涵与实质,并结合图象的对称性来分析与应用.
由d≠0,利用二次函数的图象与性质,
可知Si(i=1,2,3,……,100)中S5=0,S2=S3=-3d,S1=S4=-2d,S6=3d,S7=7d,……,其余各项均不相等.
所以Si(i=1,2,3,……,100)中不同的数值有100-2=98(个).
故填答案:98.
2 环节二:抓住问题本质,合理切入突破
解题过程中,审题时要注意题设条件中的一些关键性字、词、句等,抓住问题的本质,为解题突破口与切入点的寻找提供依据,也是数学思维的关键点.
例2 (2022年高考数学新高考Ⅰ卷·5)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为().
审题:以古典概型的形式设置问题,抓住题中的关键词“2个数互质”,结合计数原理与排列组合、概率等相关知识来综合与应用.特别,针对关键词的理解与切入,当中隐藏一组特殊的数(3,6),这里容易遗漏而导致错误.
解析:依题知,从7个整数中随机取2个不同的数的不同取法种数共有C27=21种.
所取的2个数不互质的不同取法有(2,4),(2,6),(2,8),(3,6),(4,6),(4,8),(6,8),共7种.
3 环节三:善于变形转化,实现化繁为简
在具体解题过程中,审题时要善于对题设中给出的已知条件或所求的结论形式进行必要的变形与简化,这是实现化繁为简,有效寻找解题方法和途径的一种基本策略与技巧方法.
4 环节四:寻求问题转换,巧妙化生为熟
数学审题时,不能只停留在问题的题设条件上,要合理转换,将题设条件转变成比较熟悉与典型的模型或问题,实现化生为熟,合理变形与转化.常见的有化实际问题为数学问题,化几何(或代数)问题为代数(或几何)问题,化代数问题为三角问题,等等.
例4 (2022年高考数学新高考Ⅱ卷·12)(多选题)对任意x,y,x2+y2-xy=1,则().
A.x+y≤1
B.x+y≥-2
C.x2+y2≤2
D.x2+y2≥1
审题:结合题设条件,直接判断不等式成立问题,涉及较多的不等式性质等,对思维与能力的要求较高.而根据条件中的二元方程加以配方处理,转化为两代数式的平方和为1的形式,引入三角参数进行转换,化代数问题为三角问题,化陌生为熟悉,即可顺利进行分析与判断.
解析:由x2+y2-xy=1,配方可得
故选择答案:BC.
5 环节五:深入挖掘条件,注意隐含信息
审题时往往需要对题设条件进行必要的再加工,进而深入挖掘条件,特别是其中隐含的一些信息、注意点及其他一些细节等,为问题的正确突破与求解扫清障碍.
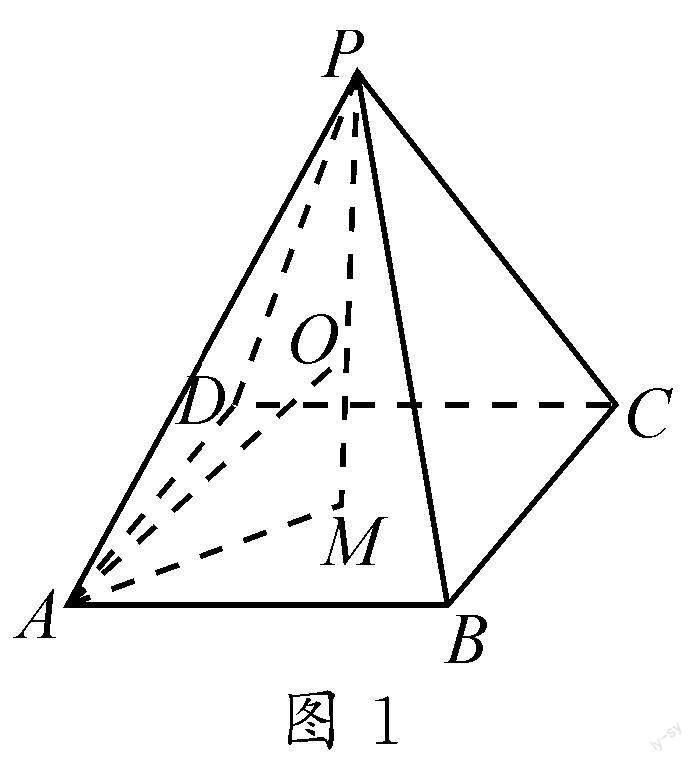
审题:结合题设条件,有一些解题者采用“极端思想”,通过题目中侧棱长的两个端点值来快速分析与求解,确定与之对应的答案,导致出错.解题时要合理挖掘条件,注意侧棱长l的变化与该正四棱锥体积变化之间的隐含关系,构建关系式来分析与处理.
解析:如图1,在正四棱锥P-ABCD中,顶点P在底面ABCD内的射影为点M,球心O在直线PM上,设球O的半径为R.
故选择答案:C.
著名数学教育家波利亚说过:“最糟糕的情况是学生没有弄清问题就进行演算和作图.”从这个意义上讲,高考数学谋试在“审”,成试在“审”,一点都不过分[2].
参考文献:
[1]陈云韬.数学多选题的审题策略技巧[J].中学数学,2022(17):49-50.
[2]张梅.数学解题的本质——审题[J].课程教材教学研究(中教研究),2022(Z4):34-35.
