高中数学“逆向教学”的实践与应用

侯晓燕

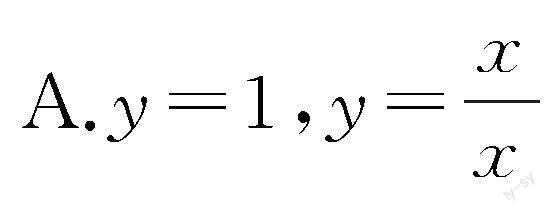
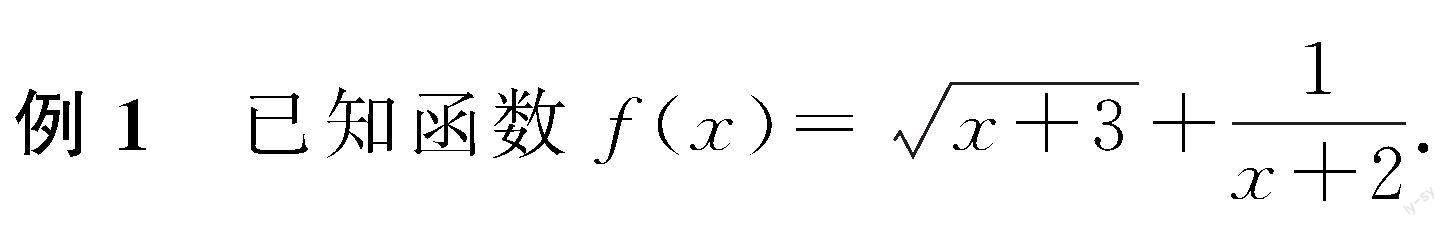
摘要：随着课程改革的深入，素质教育成为时代热词，事实上，实施素质教育是学生成长的需要、国家的需要、时代的需要.为了实现素质教育，落实课程改革，“以学定教”“以人为本”的理念必须深入每一个教师的心中.原本的数学课堂的程序大抵是“制定教学计划，实施教学过程，评价教学结果”，而逆向教学模式给数学课堂带来了激情和创新，带来了素质教育的脚踏实地.本文中以函数概念的教学为例，浅谈教学中对逆向教学的思考和应用.

关键词：逆向教学；核心素养；高中数学；概念教学

众所周知，函数概念是中学数学中最重要的概念之一，在2017年颁布的普通高中课程标准中，函数被归为必修课程中的一条重要主线，函数的思想方法几乎贯穿整个数学学习的始终[1].理解并掌握函数的概念及其反映的数学思想方法，理解函数模型，学会用函数的观点看待问题，能从实际问题中抽象出函数模型，并用函数模型解决实际问题，是高中数学素质教育的主要任务之一.因此笔者选择利用函数概念来探究逆向教学模式下的高中数学学习.

1 预设教学目标

在传统的教学设计下，学生按照教师提前设计好的思路、步骤开启学习探究活动.或许，在这个背景下，学生的思考、探究是无懈可击、环环相扣的，可是这样的思考探究始终是在教师提前搭建好的框架之内展开的，学生的思考和研究似乎被拷上了枷锁.而现在强调的逆向教学，是从教学目标或者更准确地说是从学习目标出发，将具体的学习空间赋予学生，通过自主阅读教材完成思考，自主根据核心问题进行探究，扩大了探究的范围，教师只是提出目标性的核心问题、核心任务，引导学生思考，给学生以方向上和路线上的指引[2].

2 设计目标检测题

需要强调的是，这里的目标检测题不同于教学过程中用于过渡或者阶段性检测的习题，而是可以切实检测学习目标是否完成的题目.根据本节课的学习目标，设计如下目标检测题：

（1）下列各组函数中，表示同一函数的是（）.

（3）已知f（2x+1）=x2-2x，则f（3）=.

（4）已知二次函数f（x）=x2+x+a（a>0），若f（m）<0，则f（m+1）的值为（）.

A.正数

B.负数

C.0

D.符号与a有关

3 学习活动安排及教学指导方式设计

根据逆向教学理念，本节课采取的教学活动方式是分小组讨论学习.由教师提前预设好本节课需要解决的核心问题，并在黑板上展示出来，学生的讨论围绕核心问题展开.首先，给出时间让学生自己阅读教材并思考，静默思考后，围绕核心问题以及自己在探究中产生的疑惑进行讨论，再向大家展示讨论结果.然后，由教师评价学习结果，并给出准确结论.最后，学生利用新知解题，教师通过学生对目标检测题的完成情况来总结本节课，并设计梯度作业，达到因材施教、以学定教的效果［3］.

4 教学过程设计

4.1 创设情境，揭示课题

（1）提前一天布置预习任务，复习初中所学的关于函数的知识;

（2）阅读课本引例，完成课前预习题，产生疑问之后通过思考讨论，体会函数是描述客观事物变化规律的数学模型的思想;

（3）讨论分析三个实际案例，思考并讨论这三个实例的共同点;

（4）引导学生用所学的集合语言去解释例子中变量之间的关系，判断他们是否真正理解集合语言.

4.2 研探新知

通过讨论由学生总结归纳出函数概念，由教师评价并给出准确定义.引导学生思考如下核心问题：

（1）构成函数的三要素是什么？

（2）区间的概念是什么？

（3）现在所学的函数概念与初中所学的函数概念究竟有什么不同呢？

4.3 问题探究，巩固新知

问题1 怎样求得一个函数的定义域？

（1）求函数f（x）的定义域;

（2）当a＞0时，求f（a），f（a-1）的值.

分析：如果只有函数解析式，而没有函数的实际背景，则函数的定义域只与式子有关，是指能够使这个函数式子有意义的实数的集合；而如果给出实际背景，则还需要根据实际背景考虑问题.注意函数的定义域、值域要写成集合或区间的形式.

问题2 怎样准确判断两函数是否为同一个函数？

例2 下列函数中哪些函数与函数y=x相同？

分析：①先看定义域是否相同，不相同的必然不是同一函数；再看x相同的时候，y是否也相同，不相同必然也不是同一个函数.

②当且仅当两个函数的定义域和对应关系完全一致时，则这两个函数相同，与字母无关.

4.4 巩固提升，答疑解惑

（1）完成教材第24页第2～4题；

（2）完成本节教案检测题.

4.5 归纳小结

（1）通过提前给出核心问题，结合自主阅读教材中的三个具体实例，讨论得到了函数概念，在探究中用集合与对应的语言描述了函数的定义及其相关概念［4］;

（2）了解了如何求函数的定义域以及值域的方法，掌握了判断同一个函数的基本方法，最后引出了区间的概念.

4.6 设置问题，留下悬念

（1）练习册第23页习题A组，第24页习题B组第1，2题；

（2）尝试列举两个及以上生活中的不同的函数实例，使用集合与对应的语言来描述这些函数，最后找出函数的定义域、值域及其对应关系.

5 教学反思

在“逆向教学”模式下，函数概念是由学生自主思考讨论而得来的，教师在这个过程中只是引导者.函数概念一课的教学，是高中数学的难点，难在函数概念很难讲清楚，也是第一个在初中已经给出了定义，到了高中却还要重新定义的概念.以往教学中教师们大都是反复解释定义中的各个名词和符号的含义.但是，新的“函数概念”是用“集合对应”来定义的，与初中的直观概念到底有什么关系？如果一致，为什么要换成这样的概念？这种定义和定义的变化，是本节课的根本所在[5].只有在逆向教学过程中，真正经历这个变化过程并进行深人思考，学生才能够真正理解函数的本质，而不是听教师讲之后“承认”了，“记住”了.

逆向教學设计强调的是使用教材，而不是依据教材去教教材，逆向教学设计强调评价先于教学实施，即提前设计好评价方法和目标检测题，使教学评价贯穿整节课堂.这样能充分增强逆向教学的目的性和方向性.一开始就由一个准确的教学目标和评价方式确定一个宏观的框架，教学都在这个框架里面进行，这样教师就容易对课堂中出现的不可控因素进行调控.以核心问题为导向的逆向教学设计十分适合概念教学.与传统教学相比，逆向教学更能够使学生深入理解函数概念，从教学目标出发，重视学生真正学习的发生和思维的提升，强化对知识的理解，充分体现学生是课堂的主体，有利于学生对函数概念、方法、思想的深入理解，增强其自主思考能力，真正实现素质教育.

参考文献：

［1］李剑.高中与初中数学函数概念教学的衔接研究[D].重庆：重庆师范大学，2012.

［2］赵希韶.逆向教学：促进学生“逆向学习”的设计研发[J].数学教学通讯，2021（10）：17-18.

［3］叶海龙.逆向教学设计简论[J].当代教育科学，2011（4）：23-26.

［4］章建跃，陶维林.注重学生思维参与和感悟的函数概念教学[J].数学通报，2009，48（6）：19-24，30.

［5］史宁中，濮安山.中学数学课程与教学中的函数及其思想——数学教育热点问题系列访谈录之三[J].课程＼5教材＼5教法，2007（4）：36-40.