夯实基础 关注综合

王浩宇　王红权

摘  要：分析2023年高考“集合、常用逻辑用语、不等式”专题试题，发现题型和难度相对稳定. 试题注重考查学生对基础知识的掌握、理解和运用，以及对数学思想方法的灵活运用. 通过对典型试题的解法分析和解题规律的总结，提出复习备考的建议．

关键词：集合；常用逻辑用语；不等式；试题分析；解法分析

“集合、常用逻辑用语、不等式”属于主题一“预备知识”的内容，是由初中阶段数学学习过渡到高中阶段数学学习的衔接，也是高考必考内容. 这部分知识本身难度不大，单一知识点考查以简单题为主；作为解决问题的工具考查时，往往与函数、几何等内容综合，试题难度较大，主要考查学生的数学运算和逻辑推理素养.

一、试题特点分析

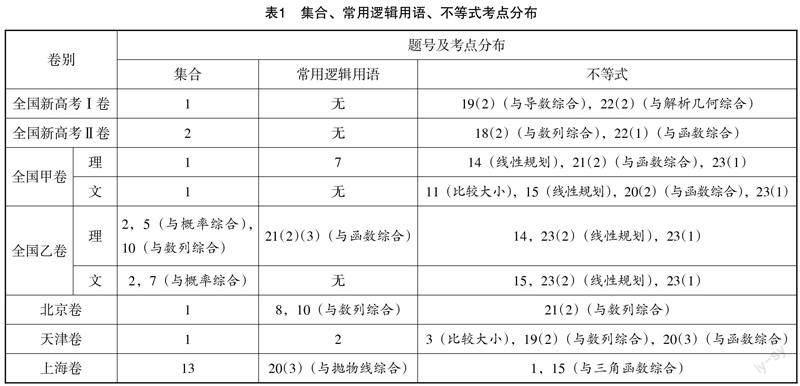
2023年高考“集合、常用逻辑用语、不等式”专题试题的考查方式并未有太大变动，基本延续2022年的命题思路. 单独考查集合、常用逻辑用语、不等式内容的试题相对较少，更多是与函数、数列等内容综合体现其工具性，具体情况如表1所示.

由表1可知，2023年高考的集合试题以单选题为主，且除上海卷外基本出现在全卷的起始位置. 主要考查集合的含义与表示（重点考查列举法和描述法）和集合间的关系与运算（包括求交集、并集和补集的运算）. 试题中规中矩、难度较小，可以安抚学生情绪，体现人文关怀.

常用逻辑用语试题以选择题为主，题量较少. 全国新高考Ⅰ卷和全国新高考Ⅱ卷中均未设置独立考查常用逻辑用语知识的试题，体现了其与全国甲卷和全国乙卷的差异. 独立成题的只有“充要条件”类试题，且全国甲卷和全国乙卷仅在理科试卷中出现，体现了文、理科试题之间的差异. 尽管“充要条件”类试题在北京卷和上海卷中也有出现，但上海卷中并未将其作为单独考点，而是以试题的限制条件出现，这种考法在2022年全国新高考Ⅰ卷第22题中出现过. 量词“任意”和“存在”没有单独试题，都是与其他知识融合成题，以工具的形式出现，往往有一定计算量.

不等式是2023年高考数学重点考查的内容之一，直接考查的有解不等式、比较大小和线性规划等. 更多的则是与函数、数列、解析几何等综合考查. 例如，利用不等式性质求定义域、值域、证明不等关系等，全面考查学生的抽象能力、推理能力和运算能力，体现了不等式的综合性和应用性.

1. 考查必备知识，注重基础性

2023年高考“集合、常用逻辑用语、不等式”专题试题注重考查基本概念和运算，考查形式通常为运算，题型多为选择题. 此类试题只需要学生掌握相应概念，能进行简单计算即可，而且能筛选粗心的学生.

目标解析：此题主要考查向量的计算与三角函数最值的求解，需要结合图象建立平面直角坐标系解决问题，考查学生的数形结合、数学运算和逻辑推理素养.

解法分析：解法1通过建立平面直角坐标系并设点为未知量，将问题转化为求动点横坐标的最小值，之后根据圆的几何特征获取动点的轨迹完成求解；解法2设角为未知量，数形结合地将问题转化为求三角函数的最值. 解法1和解法2均属于通解，解法1侧重几何，解法2侧重代数. 解法3则完全利用几何法，借助投影向量求解.

题源分析：此题的命题思路来自人教A版教材选择性必修第一册“2.4 圆的方程”课后习题中的动点问题，核心在于正确作出示意图，然后将数量积的问题转化为三角函数求最值的问题. 解题时需要数形结合，选择合适的变量对所求式子进行转化与化归，解题难度与所选的未知量有一定关系. 当不等式与其他知识模块结合后，试题的跨度大，既可以直观考查学生对相关基础知识的掌握情况，还能考查学生对知识的综合运用情况. 值得注意的是，2023年高考全国卷中未考查立体几何中的动点关系.

类题赏析：动点问题一直是学生学习的痛点，高考中的动点问题主要包括直线运动、曲线运动、抛体运动和圆周运动等. 求解方法主要是通过设未知量，利用坐标、向量和几何关系等建立方程并求解，将问题转化为函数的最值问题. 高考中的同类动点问题还有2023年天津卷第18题、2022年全国甲卷（理科）第16题（公共点问题）和2021年全国甲卷（理科）第19题（立体几何中的动点问题）等.

二、优秀试题分析

例4 （全国乙卷·理10）已知等差数列[an]的公差为[2π3]，集合S =[cosann∈N*]，若S =[a，b]，则ab的值为（    ）.

（A）-1 （B）-[12]

（C）0 （D）[12]

题意理解：此题综合考查数列、三角函数与集合知识，体现集合的工具性. 主要考查学生对等差数列通项公式、余弦函数的周期性和集合元素性质的理解. 通过试题条件可以得到等差数列[an]的通项公式，结合余弦函数的周期性和集合中元素的互异性确定集合S. 试题求解的难点在于如何将周期数列的周期为3与集合中只有两个元素相结合. 另外，要求解集合S中元素的乘积，隐藏了问题本质，在一定程度上增加了试题的难度.

思路探求：因为等差数列[an]的公差为[2π3]，所以an = a1 +[2π3n-1][=2π3]n +[a1-2π3]. 所以cos an周期为3，即cos an最多有3个不同的取值. S =[a，b]表示集合中仅存在两个元素，故同一周期内，cos an必有两个取值相同. 接下来共有3种方法能求出答案. ① 分类讨论法：对数列中相同的项进行分类讨论. 为了方便计算取数列前3项，分别讨论a1 = a2和a2 = a3. ② 特殊值法：代入容易计算的特殊值求解. ③ 分类讨论法：设前两项相等，借助三角函数的对称性，分别讨论关于x轴非负半轴对称和关于x轴非正半轴对称.

回顾反思：此题是集合、三角函数与数列的综合试题，知识的综合运用和大量的计算是这类题的设计特点. 此题考查高中数学中必须掌握的元素的基本特性，即互异性，主要考查学生的数学运算和逻辑推理能力. 解答时需要根据条件表示集合中的元素，通过推理和运算获得答案. 此题的难点在于将“同一周期内，必有一个元素相同”转化为数学式子. 解决难点共有3种方法，方法1和方法3均通过分类讨论解决难点. 其中，方法1为通解，方法3是对方法1的優化. 解题时，通过分类讨论能条理清晰地对所有情况进行研究，可以避免遗漏，但是需要学生具有较强的逻辑思维能力. 方法2属于特解，利用特殊值可以快速求解，但是需要一定的解题技巧和数学直觉.

回顾反思：此题的本质是考查指数函数的性质，培养学生的数学运算和逻辑推理等素养. 通法为作差法，对应的解法1条理清晰，有较强的思维逻辑，是高考对学生的基本要求. 作差计算较困难时，若指数、底数有相同的数字，可以借助函数的单调性求解；若有相同结构，则可以通过构造函数求解；若出现熟悉的数字，可以利用估算求解；还可以选取合适的中间值求解，考查学生的转化与化归思想.

比较大小的试题中若出现常见的无理数或熟悉的函数结构，可以使用特殊值法求解，对应此题的解法2. 通过代入具体数字求解能加快解题速度，但是需要一定的计算技巧，属于特解. 此题的创新点是根据复合函数外层函数的单调性，将问题转化为比较内层函数值的大小. 2023年高考中的同类试题还有天津卷第3题和上海卷第21题第（2）小题，其均结合其他知识考查不等式的工具性. 比较大小是2022年高考中的热点问题，2023年热度有所降低，且对应试题难度下降.

此题还可以从函数的性质角度考虑求解，即由[fx]关于x = 1对称，将[f22]，[f32]，[f62]的大小比较转化为对[22]，[32]，[62]与1的距离的比较.

回顾反思：此题将不等式与解析几何结合，不等式在其中发挥工具性作用，主要考查学生对知识的综合运用. 此题的难点在于对问题的转化，即通过设点为未知量，将矩形的周长表达为二元式子，再通过矩形邻边垂直将二元降至一元，并求得最小值. 此题求解的障碍点是计算，求导复杂，还需要利用绝对值不等式，易错点是不能同时取等的证明. 解题时，可以通过平移函数化简计算，若将函数向下平移[14]个单位长度后再证明，可以减少部分计算量.

变式设计：（1）将抛物线方程改成椭圆方程或双曲线方程；（2）将求周长的最小值改成求面积的最小值.

三、复习备考建议

集合、常用逻辑用语和不等式是高中数学中的基本内容，更是研究数学问题的工具. 作为高考必考内容，单独考查时难度较低，多出现在选择题前几题的位置. 更多时候以综合题的形式出现，考查其工具性. 通过对2023年高考“集合、常用逻辑用语、不等式”专题典型试题的解题分析，提出以下几点复习备考建议.

1. 注重基础，把握基本考点

高考更注重考查学生对概念、性质、定理本身的掌握和运用情况，于细微处着手，考查学生对知识细节的掌握. 复习过程中，需要以概念和通法为主，打好基础，做到对知识点融会贯通.

2. 关注情境，学会分析问题

集合、常用逻辑用语在高考中发挥工具性作用，通常与不等式、函数、导数、数列等进行综合考查. 这类试题的题型和难度跨度较大. 解题时，需要将问题中的“恒成立”“存在”转化为求最值问题.

不等式在高考中既作为考点，考查不等式的性质和一元二次不等式的解法，又发挥工具性作用，以主观题形式考查不等式的性质和求解. 后者往往具有情境性，复习时可以借助情境化教学，促使学生在具体情境中熟悉问题转化的技巧.

3. 感悟思想，培养核心素养

高考复习过程中，要重视学生对数学思想的感悟和掌握，依据试题结构归纳解题思路，寻找破题点. 常见的破题点有：分类讨论、函数与方程的转化、数形结合、转化与化归、反证法、构造函数等. 解题归纳能让学生回归知识本身，使得解题思路更加清晰、有条理；能促进学生数学核心素养的提升，使其遇难题而不慌.

四、典型模拟题

1. 在研究集合时，经常遇到有关集合中元素的个数问题，我们把含有限个元素的集合A叫做有限集，用Card来表示有限集合A中的元素个数. 例如：A =[a，b，c，] 则Card[A]= 3. 现有集合M =[xx≥0，x∈Z]，N =[yy=9-log2x，x>1，] 则Card[M∩N]等于      .

参考文献：

［1］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［2］曹媛，李金生. 重视基本概念原理  强调数学思维方法：2022年高考“集合、常用逻辑用语、不等式”专题解题分析［J］. 中国数学教育（高中版），2022（7 / 8）：21-31，40.

作者简介：王浩宇（1998— ），男，二級教师，主要从事课题教学研究；

王红权（1970— ），男，高级教师，浙江省特级教师，主要从事中学数学教学研究.