基于辅助函数法的耦合Shrdinger－KdV方程的函数解研究

蔡高明

（湄洲湾职业技术学院 基础教育学院，福建 莆田 351100）

随着现代科学技术的快速发展，非线性现象已经渗透到自然科学与工程技术的各个领域，越来越引起人们的重视.自然科学中的许多现象可以归结为非线性问题，如孤波混沌、吸引子、分形和逆序结构都是非线性问题［1－2］.对非线性发展方程的研究有着非常重要的价值，也一直都是数学和物理学家所关注的重要对象.在求解非线性发展方程的精确解中，新的求解方法和分析手段不断出现，一些常用的求解方法，如：辅助函数法［3］、齐次平衡法［4］、Jacobi椭圆函数展开法［5］、双曲函数法［6］等被广泛应用并不断改进，得到一些非线性偏微分方程的孤波解、扭结波解、尖波解、呼吸子解等.对于耦合Schrdinger－KdV 方程，其精确解在等离子体物理中有着广泛的应用，如可以用来描述Laugmuir波、电磁波等［7］.郝晓红等［8］讨论了Schrdinger－KdV 方程的可积性.肖婷婷［9］利用椭圆函数展开法求解Schrdinger－KdV 方程的一些精确解.徐昌智等［10］提出一种基于便映射理论的构造非线性方程行波解的方法，并用该方法求得Schrdinger－KdV 方程的 行波解.陈贺灵等［11］借助计 算机符 号计算技术，利 用F－展开法 也求得Schrdinger－KdV 方程的精确解，其中包括三角函数解、双曲函数解和椭圆函数解.在本文中，讨论α＝1，β为实数的情况，其中，u＝u（x，t）为复函数，表示复短波振幅，v＝v（x，t）为实函数，表示非线性色散介质中实长波振幅，t为时间，x表示横向传播的位移.同时，借助辅助方程研究该方程的Jacobi椭圆函数解，并分析各个解的波形图显示空间周期性和爆破性的特点.

1 利用辅助方程求解耦合Schrdinger－KdV 方程

1.1 辅助方程的原理

对于非线性发展方程的求解过程，从数学角度分析，多数是构造解的过程.将不同类型方程的解设为不同的形式，然后利用特定的思想求解具体的方程.本文利用Jacobi椭圆方程作为辅助方程，进而根据该辅助方程来解耦合Schrdinger－KdV方程的Jacobi椭圆函数解.对于给定的非线性偏微分方程

做行波变换，

其中c表示波速.将（2）式代入（1）式，方程简化为下列常微分方程

设（3）式具有如下形式的解U（ξ）＝一般地，（ξ）满足如下的辅助方程：

为获得椭圆函数解，（ξ）满足如下的辅助方程：

1.2 辅助方程法求解耦合Schrdinger－KdV 方程

引入行波变换，

其中，c、p和s为待定常数，U（ξ）和V（ξ）皆为实函数，则（6）式可化为如下的3个常微分方程：

由（10）式解得p＝.设（8）式和（9）式中U（ξ）和V（ξ）具有如下形式

其中，（ξ）满足（5），a、b和r以及ai和bi都是待定常数，n和l都是正整数.由平衡方程（8）中的最高阶线性项U″（ξ）和最高阶非线性项U（ξ）V（ξ）得到

由（12）式和（13）式，解得n＝l＝2，即（11）式化为

把（14）式代入（8）式和（9）式中，并令（ξ）的系数全为零，得到关于a0，a1，a2，b0，b1，b2，c，p，s的方程组，利用数学软件Mathematica解方程组，可得

为了便于计算，取b0＝0，则（15）可约化为

图1和图3选取的参数为m＝0.5，β＝1，c＝2.9；图2和图4选取的参数为m＝1，β＝1，c＝2.

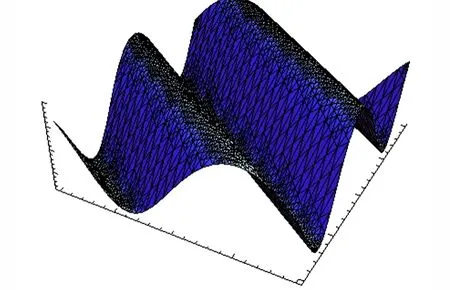
图1 u1 的三维波形图

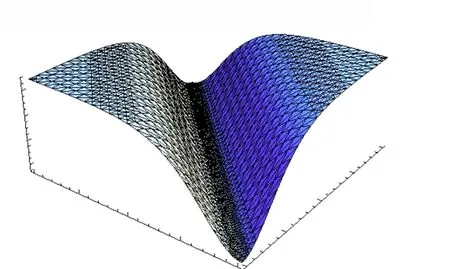
图2 u3 的三维波形图

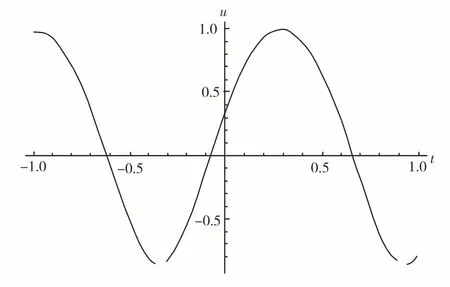
图3 u1在x ＝1时的二维波形图

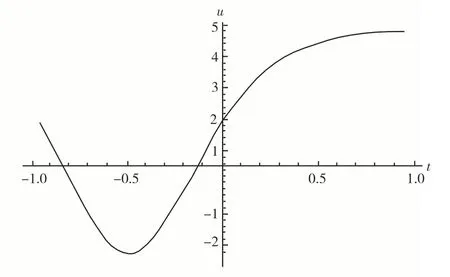
图4 u3在x ＝1时的二维波形图

2）取r＝1－m2，a＝2m2－1，b＝－2m2，0＜m＜1时，（ξ）＝cn（ξ）.把它代入（18）式，可得到方程（8）的解

图5和图7参数取m＝0.1，β＝0.1，c＝0.36；图6和图8的参数取m＝1，β＝0.1，c＝－1.6.

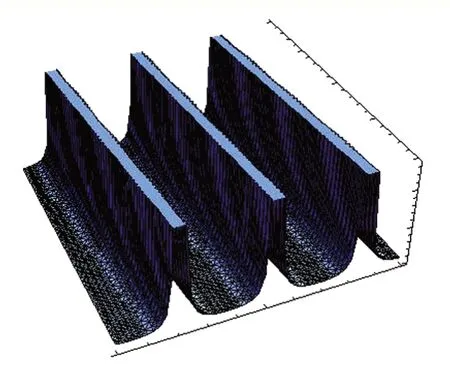
图5 u7 的三维波形图

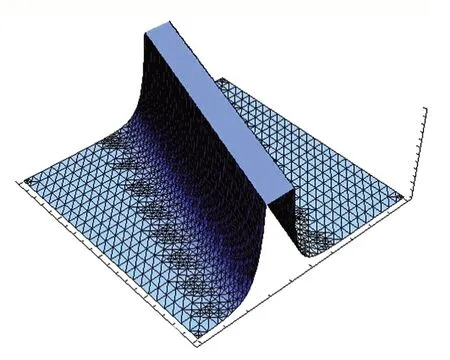
图6 u11 的三维波形图

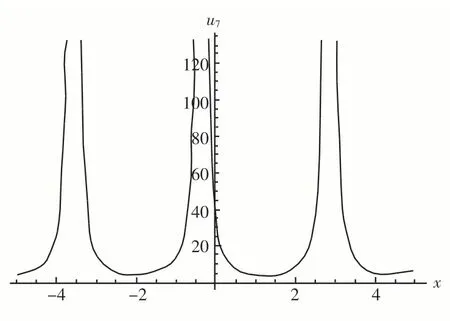
图7 u7在t＝1时的二维波形图

图8 u11在t＝1时的二维波形图

当m→1时，由（7）式可知，u17和v17皆退化为常数.

当m→1时，由（7）式可知，u20和v20退化为u16和v16.

当m→1时，由（7）式，u22和v22退化为u24和v24，即

把它代入（18）式，可得到方程（8）的解

当m→1时，由（7）式可知，u25和v25皆退化为常数.

图9 和 图10 的参数取m＝0.1，β＝0.1，c＝1.53；图11 和 图12 的参数取m＝1，β＝0.1，c＝－0.4.

图9 u22 的三维波形图

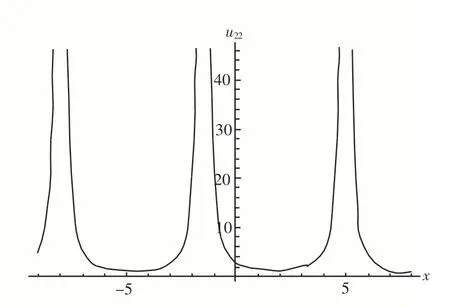
图10 u22在t＝1时的二维波形图

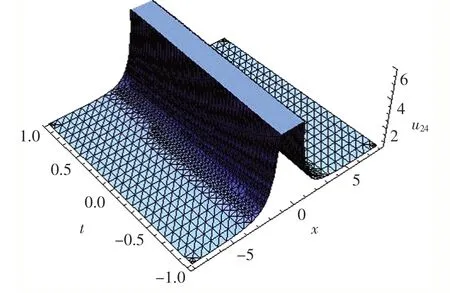
图11 u24 的三维波形图

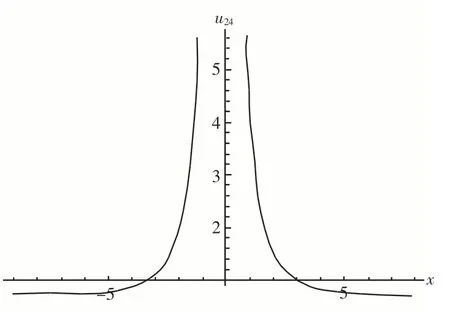
图12 u24在t＝1时的二维波形图

2 结语

本文借 助数学软件Mathematica，利用辅 助方程（ξ））2＝r＋2（ξ）＋，得到耦合Schrdinger－KdV 方程的27组解，其中有15组椭圆函数解、7组三角函数解和5组双曲函数解.对这些解的波形图的研究表明，它们具有对称性和空间周期性及爆破性的特点.此外，在本文中，可以在以下两个方面进行改进：

扩展辅助方程为

扩展方程所设的解为

从文中的求解过程可以发现，辅助方程的形式在求解过程中至关重要.因此，可以利用其他方法，如指数函数法、G′／G方法等扩展辅助方程，以期得到该辅助方程的更多解，从而丰富方程解.